CSS样式中长度单位含义解析:rpx、px、vw、vh、em、rem、pt
在 CSS 样式中,有几种常见的长度单位,包括 rpx 、 px 、 vw 和 vh 等,含义解析如下:
-
1 . rpx (响应像素): 是微信小程序中的一种相对长度单位,可以根据屏幕宽度进行自适应缩放。 1rpx 约等于屏幕宽度的 1/750 ,因此在不同设备上显示的大小会自动进行缩放,适应不同的屏幕尺寸。通常用于布局和字体大小的设置。
-
2 . px (像素): 是像素单位,表示屏幕上的一个像素点。在微信小程序中, 1px 在不同设备上的物理大小可能会有所不同,因此不具备响应性。通常用于边框、阴影等具有固定尺寸的元素。
-
3 . vw (视窗宽度的百分比): 是相对长度单位,表示相对于视窗宽度的百分比。 1vw 等于视窗宽度的 1 %。通常用于响应式布局中,根据视窗宽度的变化调整元素大小。
-
4 . vh (视窗高度的百分比): 是相对长度单位,表示相对于视窗高度的百分比。 1vh 等于视窗高度的 1 %。通常用于响应式布局中,根据视窗高度的变化调整元素大小。
-
5 . em (相对于父元素的字体大小): em 是相对长度单位,表示相对于父元素的字体大小。例如, 1em 等于父元素的字体大小。通常用于设置字体大小。
-
6 . rem (相对于根元素的字体大小): rem 是相对长度单位,表示相对于根元素( html 元素)的字体大小。例如, 1rem 等于根元素的字体大小。与 em 不同, rem 的值不会继承父元素的字体大小。通常用于响应式布局中。
-
7 . pt (点): pt 是长度单位,等于 1/72 英寸,常用于打印和排版领域。
-
8 . %(百分比): 百分比是相对长度单位,表示相对于父元素的百分比。例如, 50 % 表示父元素的一半大小。
下面是整理的一个表格,方便大家查看:
| 单位 | 特点 | 用途 |
|---|---|---|
| rpx | 相对于屏幕宽度的响应式单位,自适应缩放 | 布局和字体大小 |
| px | 固定单位,不具备响应性 | 边框、阴影等固定尺寸元素 |
| vw | 相对于视窗宽度的百分比,响应式单位 | 响应式布局 |
| vh | 相对于视窗高度的百分比,响应式单位 | 响应式布局 |
| em | 相对于父元素的字体大小 | 字体大小 |
| rem | 相对于根元素的字体大小,不受父元素影响 | 响应式布局 |
| pt | 等于1/72英寸,用于打印和排版领域 | 打印样式 |
| % | 相对于父元素的百分比 | 布局和尺寸调整 |
相关文章:

CSS样式中长度单位含义解析:rpx、px、vw、vh、em、rem、pt
在 CSS 样式中,有几种常见的长度单位,包括 rpx 、 px 、 vw 和 vh 等,含义解析如下: 1 . rpx (响应像素): 是微信小程序中的一种相对长度单位,可以根据屏幕宽度进行自适应缩放。 1rp…...
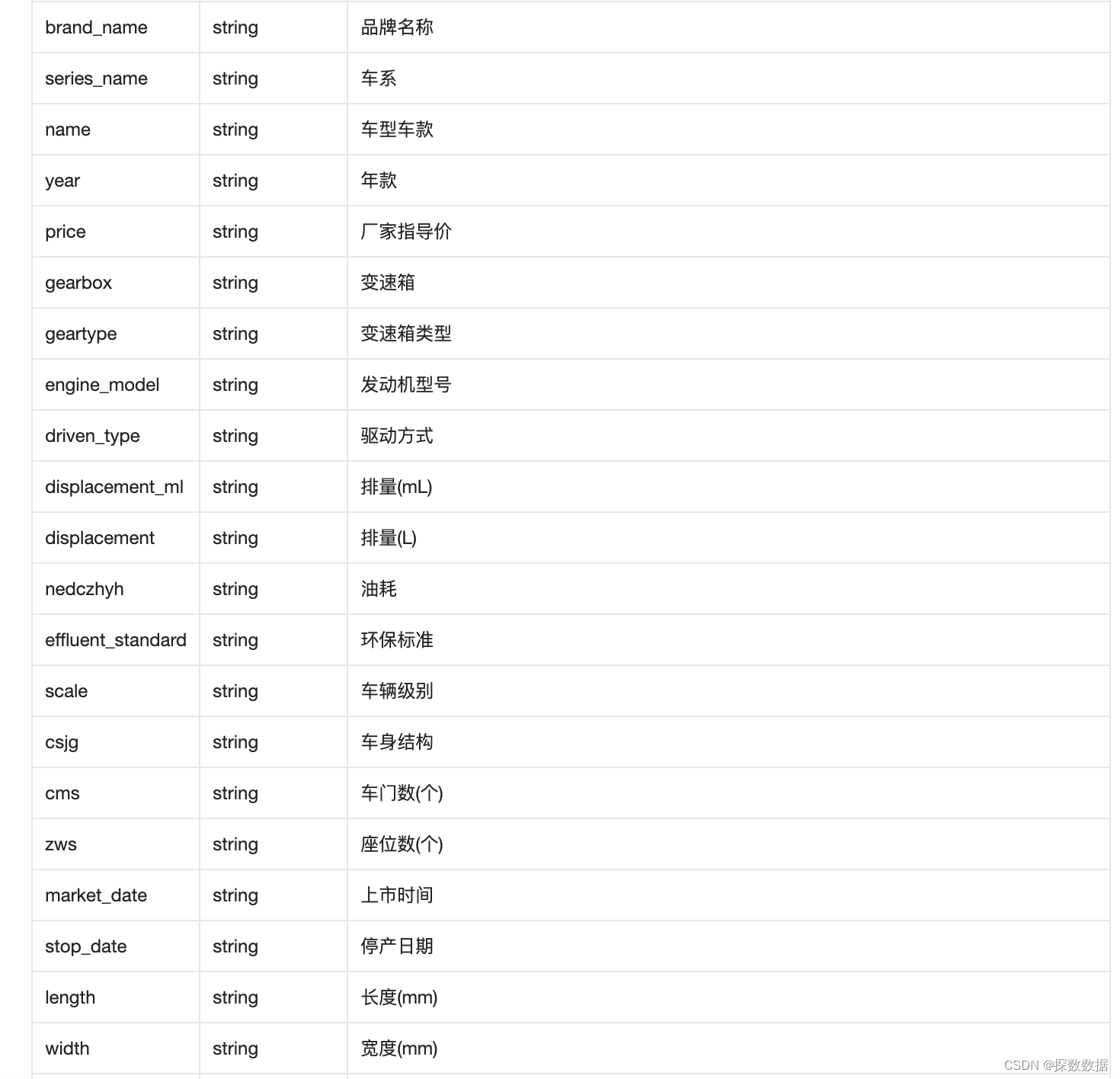
全国车辆识别代码信息API查询接口-VIN深度解析
我们先来介绍下什么是vin码,以及vin码的构成结构解析,汽车VIN码,也叫车辆识别号码,通俗可以理解为汽车的身份证号码。 VIN码一共分四大部分: 1~3位,是世界制造厂识别代号(WMI)&…...

python django 模型中字段设置blank, null属性值用法说明
问题1: ShareUser models.CharField(max_length128, blankTrue) blank设置True和false分别代表什么含义, 有什么区别?chatgpt回答的答案如下: 在 Django 模型字段中,blank 参数用于指定在创建对象时该字段是否可以为空值。它的含义如下: blankTrue:…...

暴雨信息:可持续转型更需要“以人为本”
数字化正在开启新的商业模式和价值流,为企业与组织带来巨大收益。其中,“人 (People)”这一因素至关重要。 提供更好的工作与生活体验,应对人口老龄化、劳动力短缺等挑战。对于企业而言,解决这些问题既是社会责任,也是…...
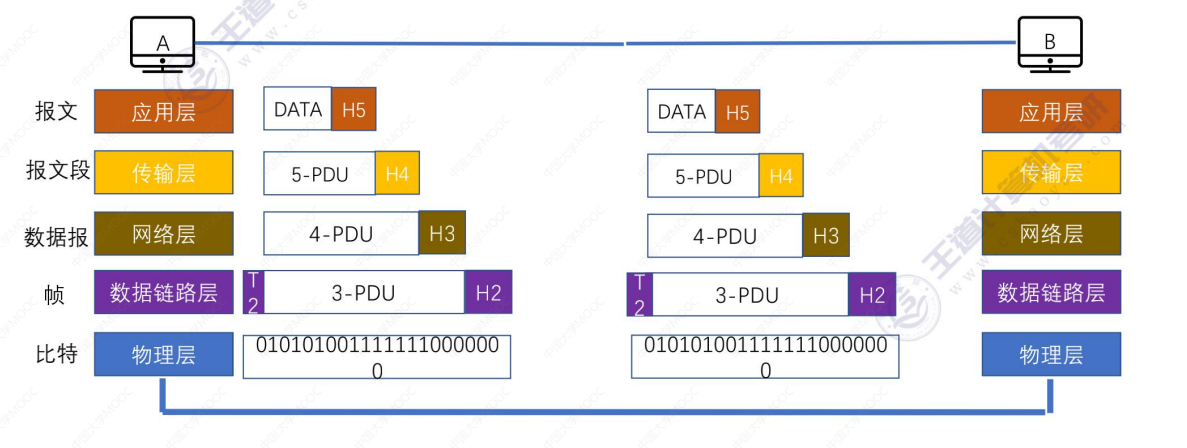
1.2_3 TCP/IP参考模型
文章目录 1.2_3 TCP/IP参考模型(一)OSI参考模型与TCP/IP参考模型(二)5层参考模型(三)5层参考模型的数据封装与解封装 1.2_3 TCP/IP参考模型 (一)OSI参考模型与TCP/IP参考模型 TCP/I…...
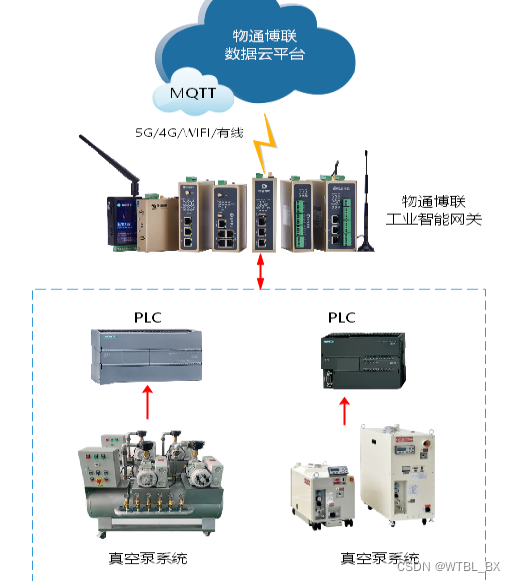
真空泵系统数据采集远程监控解决方案
行业背景 半导体制造业可以说是现代电子工业的核心产业,广泛应用于计算机、通信、汽车、医疗等领域。而在半导体生产加工过程中,如刻蚀、 镀膜、 扩散、沉积、退火等环节,真空泵都是必不可少的关键设备,它可以构建稳定受控的真空…...
Python语言在编程业界的地位——《跟老吕学Python编程》附录资料
Python语言在编程业界的地位——《跟老吕学Python编程》附录资料 ⭐️Python语言在编程业界的地位2024年3月编程语言排行榜(TIOBE前十) ⭐️Python开发语言开发环境介绍1.**IDLE**2.⭐️PyCharm3.**Anaconda**4.**Jupyter Notebook**5.**Sublime Text** …...

基于Redis自增实现全局ID生成器(详解)
本博客为个人学习笔记,学习网站与详细见:黑马程序员Redis入门到实战 P48 - P49 目录 全局ID生成器介绍 基于Redis自增实现全局ID 实现代码 全局ID生成器介绍 背景介绍 当用户在抢购商品时,就会生成订单并保存到数据库的某一张表中&#…...

hadoop 总结
1.hadoop 配置文件 core-site hdfs-site yarn-site.xml worker hdfs-site.xml <?xml version"1.0" encoding"UTF-8"?> <?xml-stylesheet type"text/xsl" href"configuration.xsl"?> <configuration><pr…...
luatos框架中LVGL如何使用中文字体〈二〉编写脚本设置中文字体
本节内容,将和大家一同学习,在luatos环境中,使用lvgl库,一步步的编译固件、编写脚本,最终实现中文字体的显示。 芯片:AIR101 LCD屏:ST7789 上一节,我们一同学习了,硬件引…...

c++单例模式和call_once函数
单例模式是一种常见的设计模式,用于确保某个类只能创建一个实例。由于单例模式是全局唯一的,因此在多线程中使用单例模式时需要考虑线程安全问题。 1.GetInstance()实例化一个对象 懒汉式:第一次用到类的时候才会去实例化。 懒汉式创建对象…...

AutoMQ 携手阿里云共同发布新一代云原生 Kafka,帮助得物有效压缩 85% Kafka 云支出!
3 月 9 日,“AutoMQ x 阿里云云原生创新论坛”在阿里巴巴西溪园区圆满落幕。本次论坛现场不仅重磅发布了新一代云原生 Kafka 产品(AutoMQ On-Prem 版),还邀请了来自得物的稳定生产负责人分享 AutoMQ 在生产场景中的应用实践&…...

力扣977. 有序数组的平方
思路:暴力法:全部平方,然后调用排序API,排序算法最快是N*log(N)时间复制度。 双指针法:要利用好原本的数组本就是有序的数组这个条件, 只是有负数 导致平方后变大了,那么平方后的最大值就是在两…...

VSCode设置
VSCode设置 VSCode设置1.双击和点击显示设置2.快捷键设置 VSCode设置 1.双击和点击显示设置 VSCode设置双击才能打开文件、文件夹 打开文件夹:在设置页中搜索 expandMode,将 singleClick 改为 doubleClick 即可。 双击打开文件:在设置页中搜索workben…...
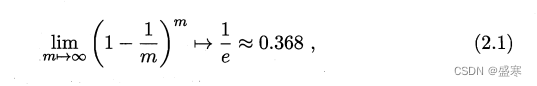
2.2 评估方法 机器学习
我们若有一个包含m个样例的数据集,若我们既需要训练,也需要测试,我们该如何处理呢?下面是几种方法: 2.2.1 留出法 “留出法”直接将数据集D划分为两个互斥的集合,其中一个作为训练集S,另一个作…...

第一类换元法(凑微分,凑狗)【高数笔记】
1.第一类换元法,解决的是什么类型的问题 2.不同的问题,应该有什么解法 3.13个基本积分公式,应该注意什么...
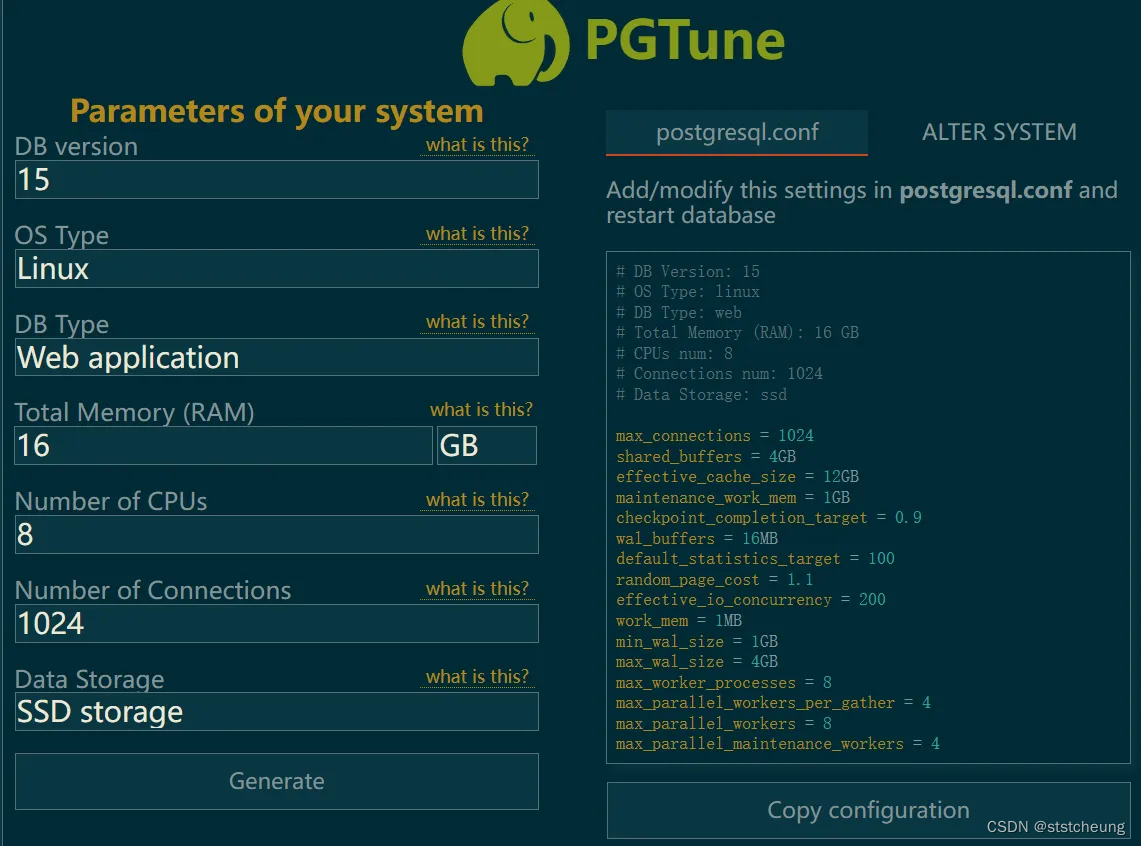
PostgreSQL数据库优化指南
默认安装下的 PostgreSQL 配置无法完全利用现有硬件,影响Netbox的性能。 本文章讲解了如何简单去优化。 优化 项目地址:https://github.com/le0pard/pgtune 首先打开:https://pgtune.leopard.in.ua/ (此网站会根据你的选择自动生成优化配置…...

VScode Error Lens插件
安装完成之后,当我们输入一些错误的语法格式的时候,它都会有一些提示! 一开始是英文提示 修改为中文提示 设置搜索 typescript.local...
Fiddler抓包教程
一、Fiddler安装: Fiddler原理 B/S模式的工作过程,简单的讲述访问一个网站的过程 。 Fiddler的位置: Fiddler是位于浏览器和服务器之间的请求和响应代理,所以它可以截获浏览器和服务器之间的所有HTTP通讯,࿰…...

TypeScript编译选项
编译单个文件:终端 tsc 文件名 自动编译单个文件:终端 tsc 文件名 -w 编译整个项目:tsc 前提是得有ts的配置文件tsconfig.json 自动编译整个项目:tsc --w tsconfig.json默认文件内容: tsconfig.json是ts编译器的配…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
