小美的平衡矩阵_dp思路
小美的平衡矩阵
写在前面:
本博客只是一种解题思路的提供。
小美的平衡矩阵
题目描述:
小美拿到了一个n*n 的矩阵,其中每个元素是 0 或者 1。
小美认为一个矩形区域是完美的,当且仅当该区域内 0 的数量恰好等于 1 的数量。
现在,小美希望你回答有多少个i*i的完美矩形区域。你需要回答1<=i<=n的所有答案。
输入描述
第一行输入一个正整数n,代表矩阵大小。
接下来的n行,每行输入一个长度为n的01 串,用来表示矩阵。
输出描述
输出n行,第i行输出的I*I 完美矩形区域的数量。
示例 1
输入
4
1010
0101
1100
0011
输出
0
7
0
1
思路:
-
符合条件的矩阵的边一定是偶数,只有偶数才能保证 0和1的数量相等
-
确定一个矩阵只需要确定这个矩阵的四个顶点中的一个和边长m,这里选择右下角的顶点
-
a r r [ i ] [ k ] arr[i][k] arr[i][k] 记录了原始输入的 n ∗ n n*n n∗n的矩阵
-
d p [ m ] [ i ] [ k ] dp[m][i][k] dp[m][i][k] 的含义是 当边长为 m 时 , 右下角为 a r r [ i ] [ k ] 时的矩阵内数字和 当边长为m时,右下角为arr[i][k]时的矩阵内数字和 当边长为m时,右下角为arr[i][k]时的矩阵内数字和
-
当矩阵内和为矩阵元素个数一半时,他是平衡矩阵。也就是说 当 m 2 2 = = d p [ m ] [ i ] [ k ] 时 \frac{m^2}{2} == dp[m][i][k]时 2m2==dp[m][i][k]时 ,这个矩阵是平衡矩阵
这里放一个 d p [ i ] [ k ] dp[i][k] dp[i][k]的版本,此时 d p [ i ] [ k ] dp[i][k] dp[i][k]的含义为:以 a r r [ 1 ] [ 1 ] arr[1][1] arr[1][1]为左上元素, a r r [ i ] [ k ] arr[i][k] arr[i][k]为右下角元素的这个框内的所有元素和,此时的平衡矩阵的个数并不在dp中保存,而是作为一个临时变量存储(这一点切记)。
#include<iostream>
#include<vector>
#include<string>
using namespace std;int main(){int N,n,i=1,k;// N用于控制输入,n用于控制输出,i和k用于访问数组的元素cin>>N;string s;// 用于记录输入的01串n = N;vector<vector<int>> arr(N+1,vector<int>(N+1));vector<vector<int>> dp(N+1,vector<int>(N+1));while(N--){k = 1;while(k<=n){cin>>s;for(char ch:s){// 遍历01串中的每个字符,将其数字放入arr中arr[i][k++] = ch-'0';}++i;}}// 计算dp数组for(i = 1;i<=n;++i){for(k = 1;k<=n;++k){dp[i][k] = dp[i-1][k]+dp[i][k-1]-dp[i-1][k-1]+arr[i][k]; }}for(int m = 1;m<=n;++m){// 矩阵边长为1开始遍历,直到边长为nint ans = 0;if(m%2==0){// 只有边长为偶数的矩阵内才有可能使得 0和1的数目相等,保证可能存在平衡矩阵for(i = 1;i<=n;++i){for(k = 1;k<=n;++k){if(i>=m&&k>=m){unsigned long long num = dp[i][k]-dp[i-m][k]-dp[i][k-m]+dp[i-m][k-m];if(num==m*m/2)ans++;}}}}cout<<ans<<endl;}return 0;
}
有什么问题欢迎来讨论。
最开始思路:
d p [ r ] [ q ] [ i ] [ k ] dp[r][q][i][k] dp[r][q][i][k] 保存 以 a r r [ r ] [ q ] arr[r][q] arr[r][q]为左上角 a r r [ i ] [ k ] arr[i][k] arr[i][k] 为右下角的框内的元素和,发现dp的初始化和计算都比较麻烦,而且也计算了很多不符合条件的框(非正方形框)
稍微改进
d p [ m ] [ i ] [ k ] dp[m][i][k] dp[m][i][k] 保存 边长为 m m m时,框的右下角为元素 a r r [ i ] [ k ] arr[i][k] arr[i][k]时的这个框内的所有元素和,刨除了非正方形的框,
最后:
d p [ i ] [ k ] dp[i][k] dp[i][k] ,也就是代码版本
注意:本程序仅由简单测试,主要是提供思路。相关文章:

小美的平衡矩阵_dp思路
小美的平衡矩阵 写在前面: 本博客只是一种解题思路的提供。 小美的平衡矩阵 题目描述: 小美拿到了一个n*n 的矩阵,其中每个元素是 0 或者 1。 小美认为一个矩形区域是完美的,当且仅当该区域内 0 的数量恰好等于 1 的数量。 现在…...

json展示curl 请求接口返回结果
使用curl发送请求并将返回结果以JSON格式展示,通常需要确保请求的响应本身就是JSON格式。可以结合jq这个JSON处理工具来格式化输出。 首先要安装jq 工具。 Linux发行版中,你可以使用包管理器来安装它。 sudo yum install jq # 对于CentOS/RHEL 安装成…...

2024 年排名前 5 名的 Mac 数据恢复软件分享
如果您已经在 Mac 上丢失了数据并且正在寻找恢复数据的方法,那么您来对地方了。互联网上有超过 50 个适用于 Mac 的数据恢复程序。哪个是最好的 Mac 数据恢复软件?不用担心。本文列出了 5 款 Mac 数据恢复软件,可帮助您在 Mac OS 下恢复丢失的…...

请描述一下Spring MVC的工作流程。在Spring MVC中,DispatcherServlet的作用是什么?
请描述一下Spring MVC的工作流程。 Spring MVC 的工作流程是基于请求驱动的,它围绕 Servlet 设计,将请求映射到处理器,处理器处理请求并返回响应。以下是 Spring MVC 的基本工作流程: 发送请求: 客户端(例…...

2023年终总结——跌跌撞撞不断修正
目录 一、回顾1.一月,鼓足信心的开始2.二月,焦躁不安3.三月,路还是要一步一步的走4.四月,平平淡淡的前行5.五月,轰轰烈烈的前行6.六月,看事情更底层透彻了7.七月,设计模式升华月8.八月ÿ…...
OPPO后端二面,凉了!
这篇文章的问题来源于一个读者之前分享的 OPPO 后端凉经,我对比较典型的一些问题进行了分类并给出了详细的参考答案。希望能对正在参加面试的朋友们能够有点帮助! Java String 为什么是不可变的? public final class String implements java.io.Seri…...

Unity3d版白银城地图
将老外之前拼接的Unity3d版白银城地图,导入到国内某手游里,改成它的客户端地图模式,可以体验一把手游的快乐。 人物角色用的是它原版的手游默认的,城内显示效果很好,大家可以仔细看看。 由于前期在导入时遇到重大挫折&…...

【PCL】(二十八)点云超体素分割
(二十九)点云超体素分割 论文:Voxel Cloud Connectivity Segmentation - Supervoxels for Point Clouds supervoxel_clustering.cpp #include <pcl/console/parse.h> #include <pcl/point_cloud.h> #include <pcl/point_ty…...

Socket通信Demo(Unity客户端和C#)
Socket通信基本流程 首先要启动服务器创建Socket,然后要绑定服务器的一个端口这样客户端通过服务器IP端口号就能连接到服务器了服务器接下来会设置监听队列,监听并等待要连接到它的客户端客户端在服务器启动之后也建立自己的Socket,然后使用…...

Lucene 自定义词库
import org.apache.lucene.analysis.hunspell.Dictionary; import org.apache.lucene.analysis.hunspell.HunspellStemFilter; import...

【LeetCode热题100】73. 矩阵置零(矩阵)
一.题目要求 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 二.题目难度 中等 三.输入样例 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0…...
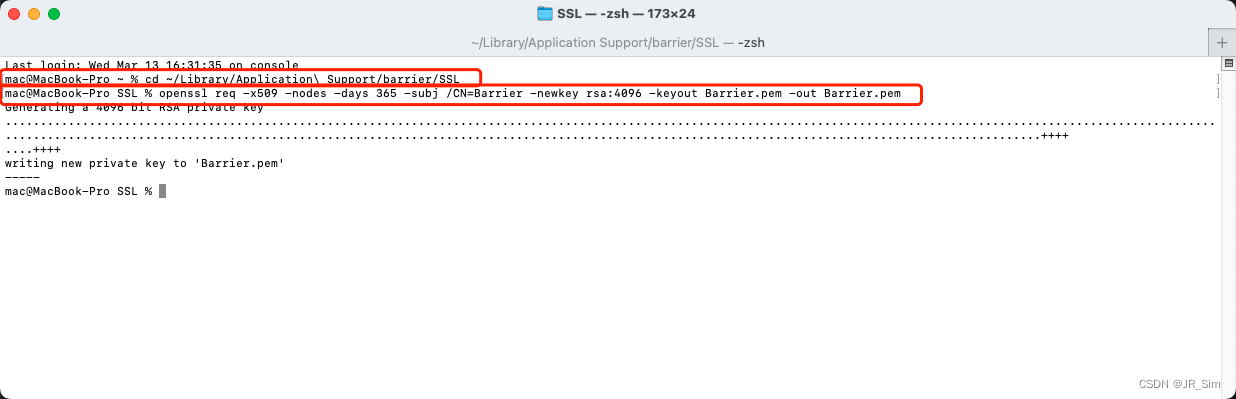
使用Barrier共享鼠标键盘,通过macos控制ubuntu系统
之前文章写过如何使用barrrier通过windows系统控制ubuntu系统,该文章将详细介绍如何使用barrier通过macos系统控制ubuntu系统 一、macOS安装barrier macOS版本barrier链接 1、双击点开安装包 2、将安装包里的barrier拷贝到macOS的达达->应用程序中 3、在达达…...
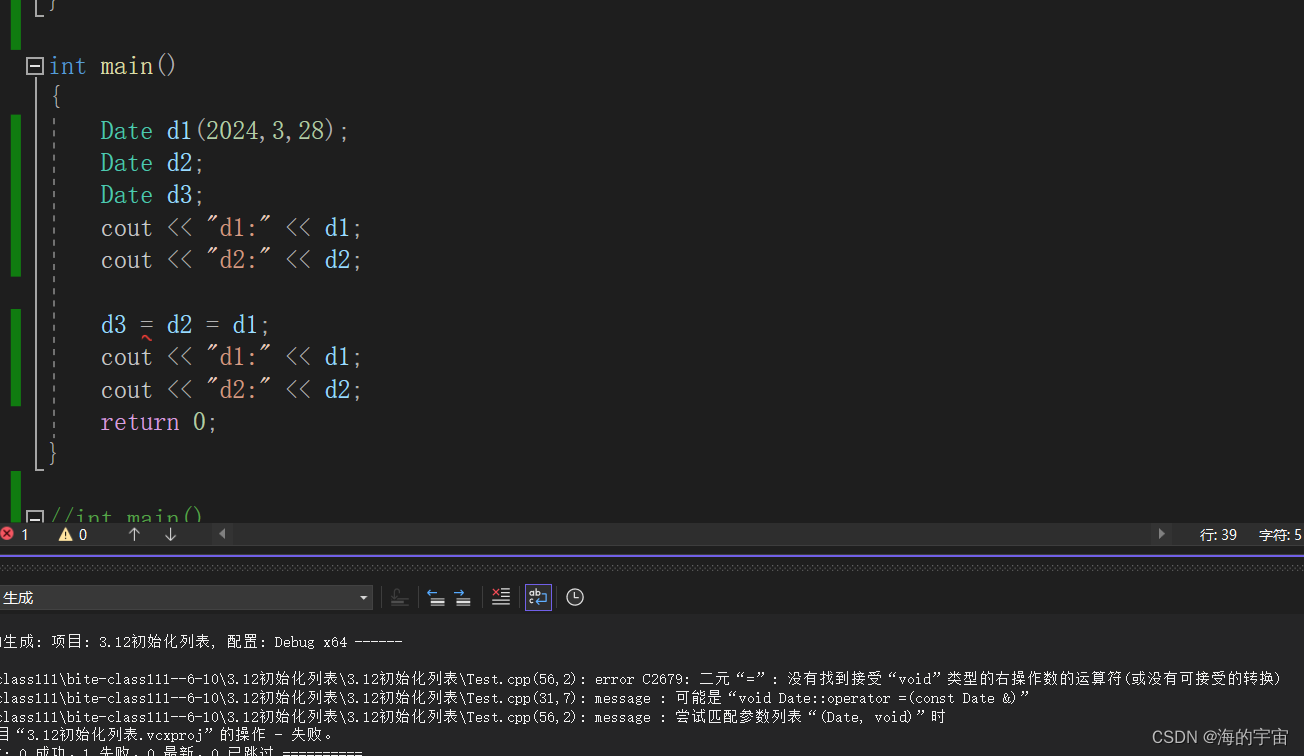
c++:类和对象中:拷贝构造和赋值运算符重载详解
c:类和对象 构造函数和析构函数详解 文章目录 c:类和对象构造函数和析构函数详解 前言一、拷贝构造怎么写拷贝构造1.拷贝构造也是构造函数的一种,构造函数没有值.所以拷贝构造也没有返回值**2.拷贝构造只有一个形参,正常这个形参是自定义类型对象的引用.3. 如果我们没有显示写…...
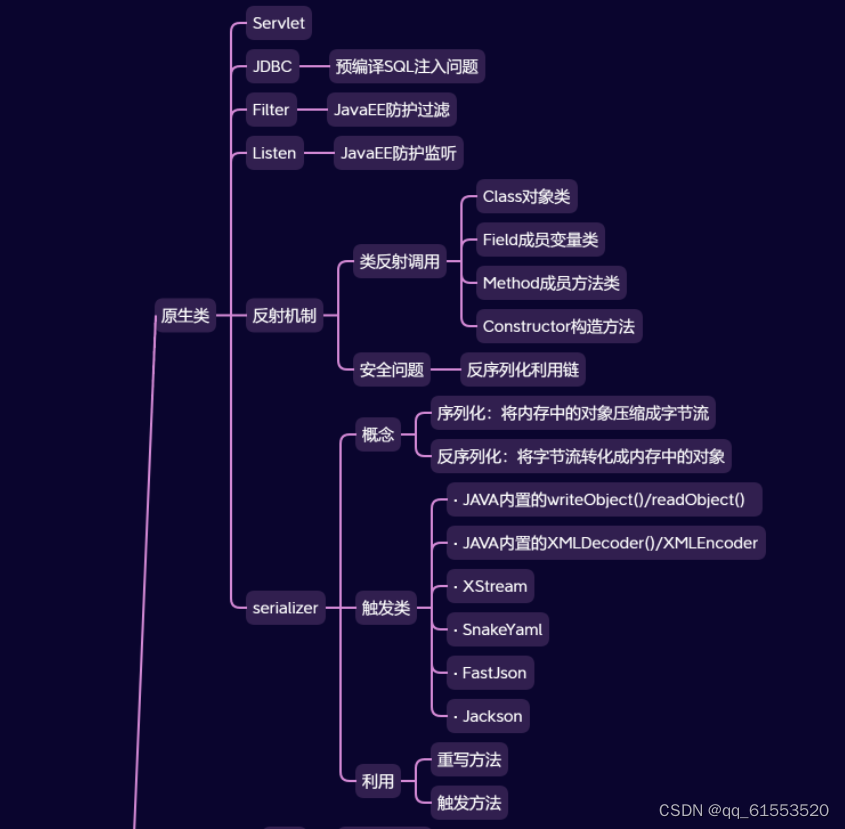
Day33:安全开发-JavaEE应用SQL预编译Filter过滤器Listener监听器访问控制
目录 JavaEE-预编译-SQL JavaEE-过滤器-Filter JavaEE-监听器-Listen 思维导图 Java知识点 功能:数据库操作,文件操作,序列化数据,身份验证,框架开发,第三方库使用等. 框架库:MyBatis&#…...

Log4j如何支持多线程环境?你如何优化Log4j的性能?
Log4j如何支持多线程环境? Log4j 通过其内部设计来支持多线程环境,确保在多线程应用程序中能够安全地使用。以下是 Log4j 支持多线程环境的一些关键方面: 线程安全性: Log4j 的 Logger 类和 Appender 类都是设计为线程安全的。这…...

golang sync.Pool 指针数据覆盖问题
场景 1. sync.Pool设置 var stringPool sync.Pool{New: func() any {return new([]string)}, }func NewString() *[]string {v : stringPool.Get().(*[]string)return v }func PutString(s *[]string) {if s nil {return}if cap(*s) > 2048 {s nil} else {*s (*s)[:0]…...

VUE+内置iframe传值失效问题解决
起因: 公司业务需要计算建筑物截收面积,然后我采用的是openCV来计算,在vue内部引用不了,然后就采用了iframe原生html来完成;功能实现了我想让iframe和vue通信;然后用原有方式试了多次都失败了,i…...
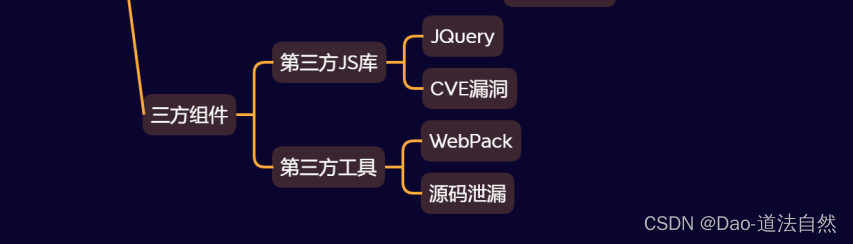
Day31:安全开发-JS应用WebPack打包器第三方库JQuery安装使用安全检测
目录 打包器-WebPack-使用&安全 第三方库-JQuery-使用&安全 思维导图 JS知识点: 功能:登录验证,文件操作,SQL操作,云应用接入,框架开发,打包器使用等 技术:原生开发&…...
回顾api服务和rpc服务的本质)
Go Zero微服务个人探究之路(十六)回顾api服务和rpc服务的本质
目录 前言 正文 API(Application Programming Interface) RPC(Remote Procedure Call) API 与 RPC 的关系 分布式部署 API 和 RPC 结语 前言 go-zero 是一个基于 Go 语言的微服务框架,它提供了一套简洁的编程模…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的夜间车辆检测系统(深度学习代码+UI界面+训练数据集)
摘要:开发夜间车辆检测系统对于自动驾驶技术具有关键作用。本篇博客详细介绍了如何运用深度学习构建一个夜间车辆检测系统,并提供了完整的实现代码。该系统基于强大的YOLOv8算法,并对比了YOLOv7、YOLOv6、YOLOv5,展示了不同模型间…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
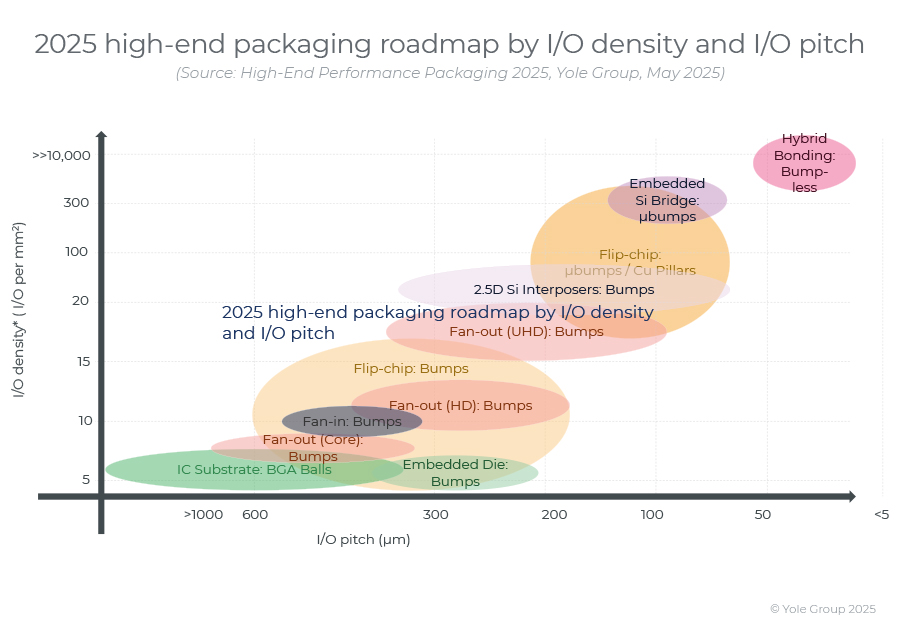
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
