MongoDB聚合运算符:$dayOfWeek
$dayOfWeek返回日期中“星期”的部分,值的范围1-7,即Sunday~Saturday。
语法
{ $dayOfWeek: <dateExpression> }
参数说明:
<dateExpression>为可被解析为Date、Timestamp或ObjectID的表达式<dateExpression>也可以是一个文档{ date: <dateExpression>, timezone: <tzExpression> }date是可以被解析为Date、Timestamp或ObjectID的表达式timezone可选,操作结果的时区
使用
下面通过示例对使用规则进行说明:
例1
{ $dayOfWeek: new Date("2016-01-01") }
结果:6
例2
{ $dayOfWeek: { date: new Date("Jan 7, 2003") } }
结果:3
例3
{ $dayOfWeek: {date: new Date("August 14, 2011"),timezone: "America/Chicago"
} }
结果:1
例4
{ $dayOfWeek: ISODate("1998-11-07T00:00:00Z") }
结果:7
例5
{ $dayOfWeek: {date: ISODate("1998-11-07T00:00:00Z"),timezone: "-0400"
} }
结果:6
例6
{ $dayOfWeek: "March 28, 1976" }
结果:error
例7
{ $dayOfWeek: Date("2016-01-01") }
结果:error
例8
{ $dayOfWeek: "2009-04-09" }
结果:error
举例
sales集合有下面的文档:
{"_id" : 1,"item" : "abc","price" : 10,"quantity" : 2,"date" : ISODate("2014-01-01T08:15:39.736Z")
}
下面的聚合使用$dayOfWeek和其他日期运算符来分解日期字段:
db.sales.aggregate([{$project:{year: { $year: "$date" },month: { $month: "$date" },day: { $dayOfWeek: "$date" },hour: { $hour: "$date" },minutes: { $minute: "$date" },seconds: { $second: "$date" },milliseconds: { $millisecond: "$date" },dayOfYear: { $dayOfYear: "$date" },dayOfWeek: { $dayOfWeek: "$date" },week: { $week: "$date" }}}]
)
操作返回下面的结果:
{"_id" : 1,"year" : 2014,"month" : 1,"day" : 1,"hour" : 8,"minutes" : 15,"seconds" : 39,"milliseconds" : 736,"dayOfYear" : 1,"dayOfWeek" : 4,"week" : 0
}
相关文章:

MongoDB聚合运算符:$dayOfWeek
$dayOfWeek返回日期中“星期”的部分,值的范围1-7,即Sunday~Saturday。 语法 { $dayOfWeek: <dateExpression> }参数说明: <dateExpression>为可被解析为Date、Timestamp或ObjectID的表达式<dateExpression>也可以是一个…...

Visual Studio单步调试中监视窗口变灰的问题
在vs调试中,写了这样一条语句 while((nfread(buf, sizeof(float), N, pf))>0) 然而,在调试中,只要一执行while这条语句,监视窗口中的变量全部变为灰色,不能查看,是程序本身并没有报错,能够继…...
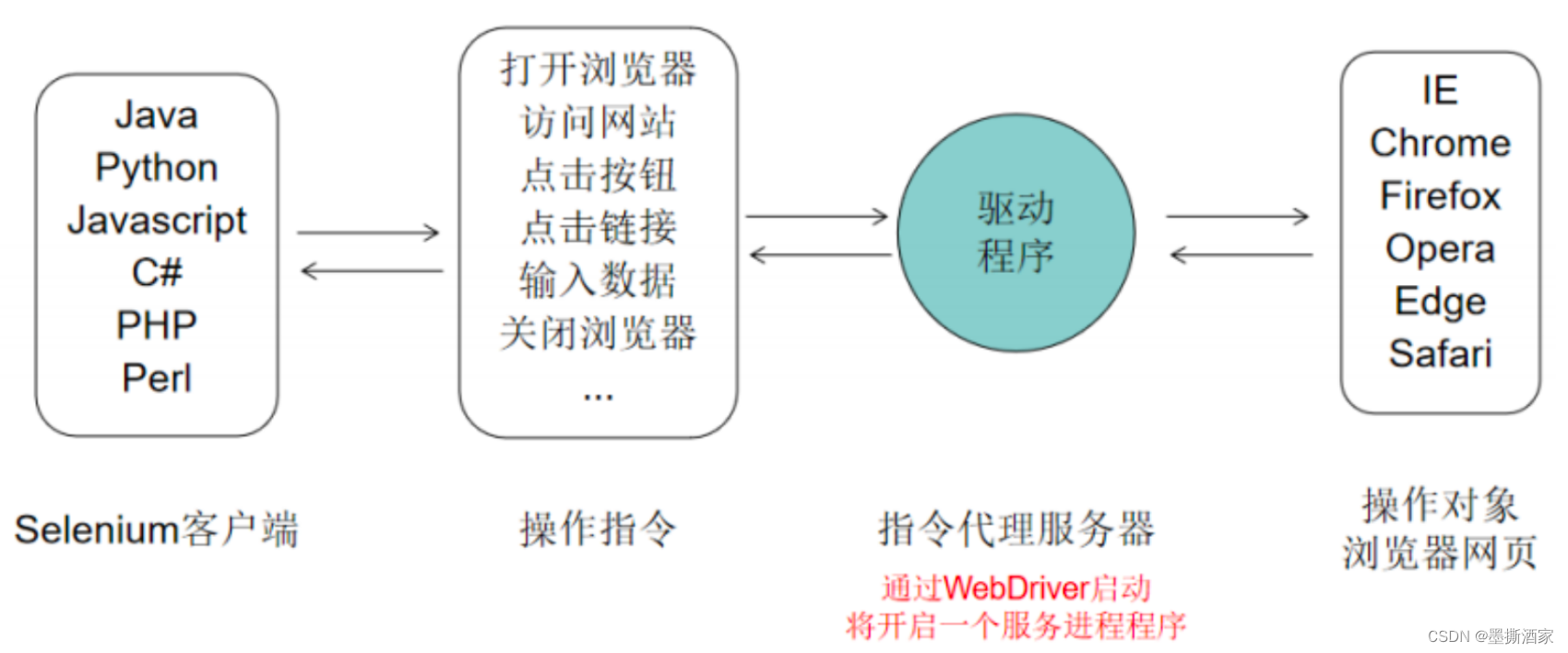
【Selenium】selenium介绍及工作原理
一、Selenium介绍 用于Web应用程序测试的工具,Selenium是开源并且免费的,覆盖IE、Chrome、FireFox、Safari等主流浏览器,通过在不同浏览器中运行自动化测试。支持Java、Python、Net、Perl等编程语言进行自动化测试脚本编写。 官网地址&…...
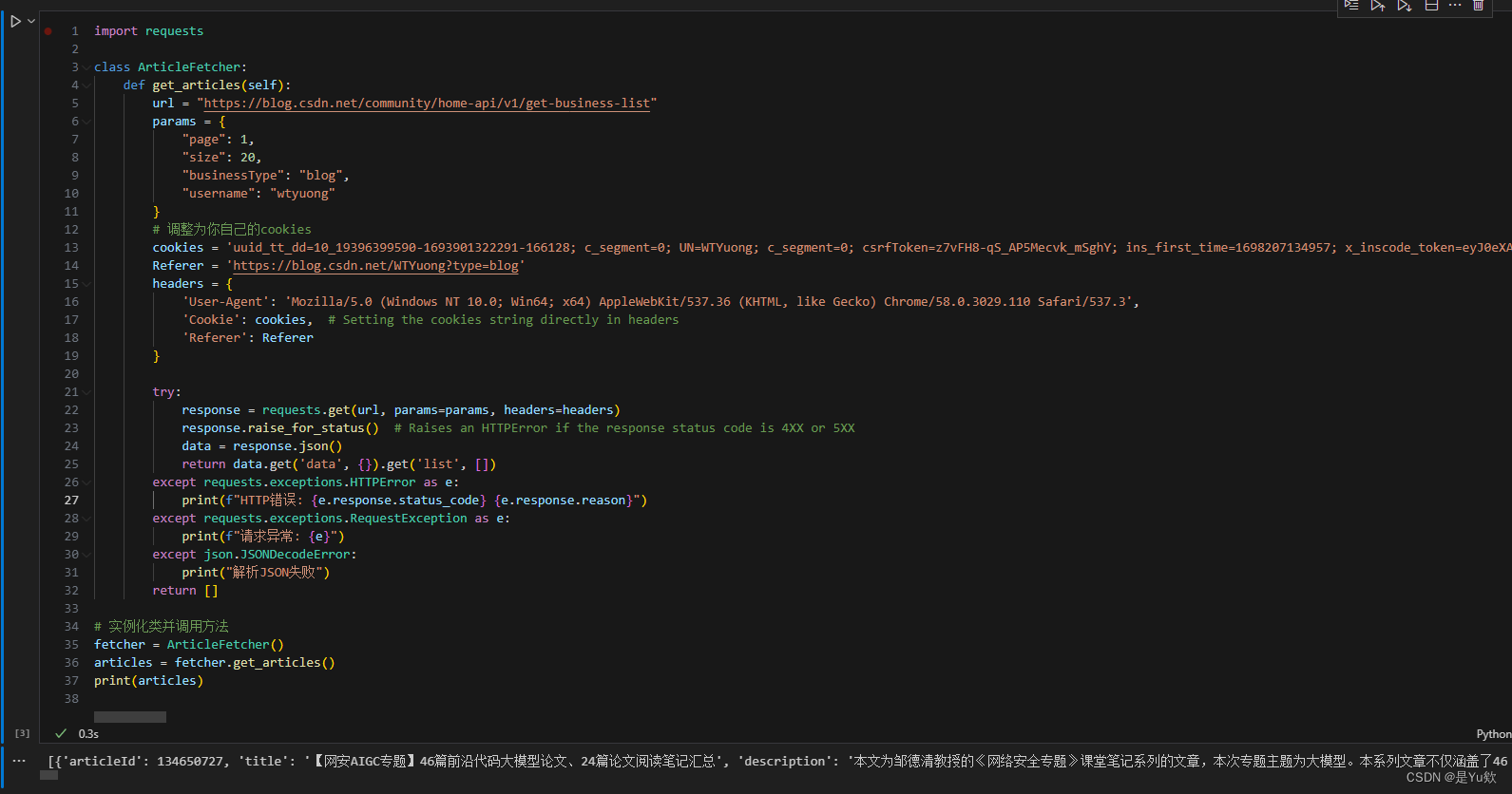
【2024-完整版】python爬虫 批量查询自己所有CSDN文章的质量分:附整个实现流程
【2024】批量查询CSDN文章质量分 写在最前面一、分析获取步骤二、获取文章列表1. 前期准备2. 获取文章的接口3. 接口测试(更新重点) 三、查询质量分1. 前期准备2. 获取文章的接口3. 接口测试 四、python代码实现1. 分步实现2. 批量获取文章信息3. 从exce…...

Nuxt3: useFetch使用过程常见一种报错
一、问题描述 先看一段代码: <script setup> const fetchData async () > {const { data, error } await useFetch(https://api.publicapis.org/entries);const { data: data2, error: error2 } await useFetch(https://api.publicapis.org/entries);…...

当代计算机语言占比分析
在当今快速发展的科技领域,计算机语言作为程序员的工具之一,扮演着至关重要的角色。随着技术的不断演进,各种编程语言层出不穷,但在实际开发中,哪些计算机语言占据主导地位?本文将对当代计算机语言的占比进…...
基于大模型和向量数据库的 RAG 示例
1 RAG 介绍 RAG是一种先进的自然语言处理方法,它结合了信息检索和文本生成技术,用于提高问答系统、聊天机器人等应用的性能。 2 RAG 的工作流程 文档加载(Document Loading) 从各种来源加载大量文档数据。这些文档…...
【C语言】比较两个字符串大小,strcmp函数
目录 一,strcmp函数 1,strcmp函数 2,函数头文件: 3,函数原型: 4,返回取值: 二,代码实现 三,小结 一,strcmp函数 1,strcmp函数 …...

深入理解与应用Keepalive机制
目录 引言 一、VRRP协议 (一)VRRP概述 1.诞生背景 2.基本理论 (二)VRRP工作原理 (三)VRRP相关术语 二、keepalive基本理论 (一)基本性能 (二)实现原…...

嵌入(embedding)概念
嵌入(embedding)在数学和相关领域中的确是指将一个数学对象在保持其某些关键性质不变的前提下,注入到一个更大或更高维的空间中。这个过程不仅仅是简单的映射,而是要求注入的对象在新空间中的表现形式能够完整反映原有对象的内在结…...
豆瓣书影音存入Notion
使用Python将图书和影视数据存放入Notion中。 🖼️介绍 环境 Python 3.10 (建议 3.11 及以上)Pycharm / Vs Code / Vs Code Studio 项目结构 │ .env │ main.py - 主函数、执行程序 │ new_book.txt - 上一次更新书籍 │ new_video.…...

Lucene 分词 示例代码
import org.apache.lucene.analysis.tokenattributes.CharTermAttribute; import org.apache.lucene.analysis.TokenStream; import org...

2.18 校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、自动驾驶一周资讯 - 李想回应“年终奖有点大”;智界升级为奇瑞独立事业部;小鹏汽车春节累计智驾总里程公布 自动驾驶一周资讯 - 李想回应“年终奖有点大”&…...

spring中事务失效的场景有哪些?
异常捕获处理 在方法中已经将异常捕获处理掉并没有抛出。 事务只有捕捉到了抛出的异常才可以进行处理,如果有异常业务中直接捕获处理掉没有抛出,事务是无法感知到的。 解决:在catch块throw抛出异常。 抛出检查异常 spring默认只会回滚非检…...
Visual Studio 2022之Release版本程序发送到其它计算机运行
目录 1、缺少dll 2、应用程序无法正常启动 3、This application failed to start because no Qt platform plugin could be initialized. 代码在Debug模式下正常运行,然后切换到Release模式下,也正常运行,把第三方平台的dll拷贝到exe所在…...
.)
Xcode下载模拟器报错Could not download iOS 17.4 Simulator (21E213).
xcode14以后最小化安装包,从而将模拟器不集中在安装包中 因此xcode14至以后的版本安装后第一次启动会加载提示安装模拟器的提示框 或者根据需要到xcode中进行所需版本|平台的模拟器进行安装 Xcode > Settings > Platforms 问题来了尝试多次都安装失败例如…...

mac在终端设置代理
前言 本篇文章介绍如何在mac终端设置代理服务器,有时候,我们需要在终端进行外网的资源访问,比如我构建v8引擎项目的时候,需要使用gclient更新组件和下载构建工具。如果单单设置了计算机的代理,依然是无法下载资源的&a…...

傅立叶之美:深入研究傅里叶分析背后的原理和数学
一、说明 T傅里叶级数及其伴随的推导是数学在现实世界中最迷人的应用之一。我一直主张通过理解数学来理解我们周围的世界。从使用线性代数设计神经网络,从混沌理论理解太阳系,到弦理论理解宇宙的基本组成部分,数学无处不在。 当然,…...
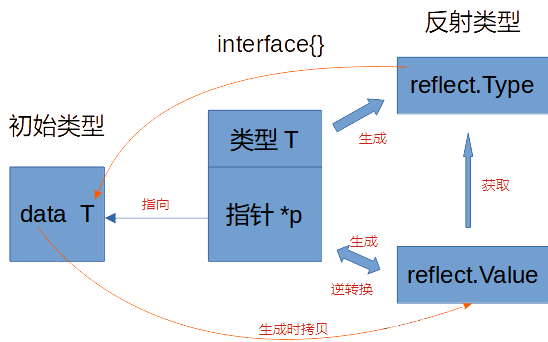
golang学习随便记16-反射
为什么需要反射 下面的例子中编写一个 Sprint 函数,只有1个参数(类型不定),返回和 fmt.Fprintf 类似的格式化后的字符串。实现方法大致为:如果参数类型本身实现了 String() 方法,那调用 String() 方法即可…...

识别恶意IP地址的有效方法
在互联网的环境中,恶意IP地址可能会对网络安全造成严重威胁,例如发起网络攻击、传播恶意软件等。因此,识别恶意IP地址是保护网络安全的重要一环。IP数据云将探讨一些有效的方法来识别恶意IP地址。 IP地址查询:https://www.ipdata…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
