傅立叶之美:深入研究傅里叶分析背后的原理和数学

一、说明
T傅里叶级数及其伴随的推导是数学在现实世界中最迷人的应用之一。我一直主张通过理解数学来理解我们周围的世界。从使用线性代数设计神经网络,从混沌理论理解太阳系,到弦理论理解宇宙的基本组成部分,数学无处不在。
当然,这些是数学中更复杂和技术性的应用。但是,将数学应用于我们的生活呢?
好吧,也许你在学习时会听双耳节拍。或者您以前做过 X 光检查。或者,您可能已经看过脑电图 (EEG) 测试的实际应用。
无论情况如何,总有一些数学算法可以促进它们的使用。
但是哪种算法呢?
Welp,其中之一是傅里叶级数(及其衍生物)。
二、一丝直觉
傅里叶级数及其推导的核心是数学算法,旨在将信号从时域转换为频域。
在一段时间内分析时域中的信号。
在频域的功率谱上分析频域中的信号
它通过接收信号函数并将其分解为具有不同频率和不同功率水平的正弦函数的总和来做到这一点。

傅里叶级数的一个非常基本的表示。
从傅里叶级数中,我们可以推导出连续傅里叶变换,它可以让我们隔离构成信号的各个频率分量及其相应的功率。
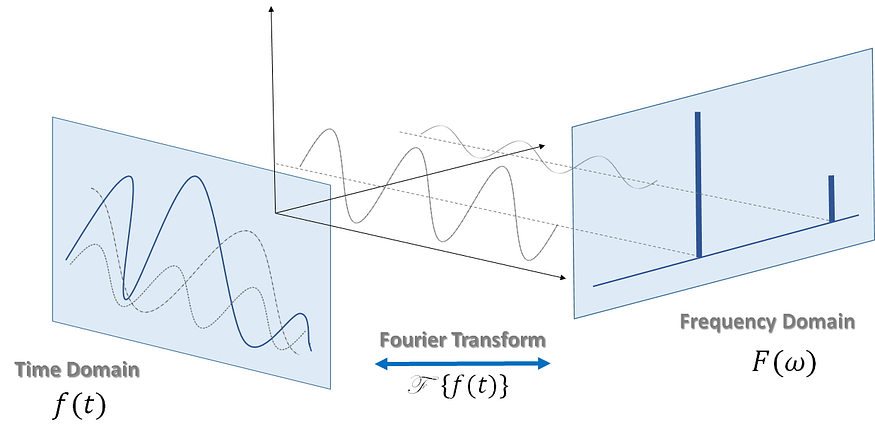
傅里叶变换的可视化。
这种变换非常有用,因为一旦我们将信号从时域转换为频域,我们就可以从信号中去除不需要的频率分量。
举个例子,假设我们使用脑电图来记录大脑信号以分析多动症。
通常,通过脑电图记录的信号非常嘈杂,不是很可靠——至少原始脑电图信号不是。
我们可以使用傅里叶级数的另一种推导,即快速傅里叶变换,以便将原始脑电信号从时域分解到频域。

时域(左)和频域(右)
从那里,我们可以通过实现带通、带阻或陷波滤波器从数据集中删除特定的频率或频率范围。
您可以清楚地看到 EEG 数据集的频域中的巨大尖峰(可能来自电力线干扰)。
这些是我们通过应用滤波器去除的频率。

过滤脑电图数据集 |感谢 FFT。
这正是我在之前的一个项目中所做的,以描述ADHD。
如果您好奇,请随时在本文或视频中查看。
在许多其他应用中也可以做到这一点,例如音频工程、图像处理、医疗诊断和语音识别。
它不受限制。
现在,您可能已经注意到,我提到了傅里叶级数的不同推导,其中一些是傅里叶变换和快速傅里叶变换。
傅里叶级数的不同推导适用于不同的上下文。有些比其他的更实用,有些则更适合数学理论。
例如,连续傅里叶变换在无限级数上获取连续的非周期信号。

连续傅里叶变换公式
但是计算机不能处理连续信号,而且很可能你需要处理更有限的信号样本。
因此,我们可以改用离散傅里叶变换,它在 N 个样本上接收有限信号。

离散傅里叶变换公式
像这样的推导使我们的生活变得更加轻松。
现在,您可以轻松地从前一个转换中从数学上推导出每个转换。

这一切都是相互关联的。
当我在脑电图和信号处理领域工作时,我对傅里叶系列必须针对不同用例进行模塑的敏捷性着迷。
因此,我决定研究并学习每个变换背后的数学原理。
让我们更深入地了解一下它是如何工作的。
三、真正的傅里叶级数
实傅里叶级数是其他派生变换的基础工具。
如前所述,它允许我们表示连续
周期性信号,即在一段时间内重复的信号,变成正弦和余弦的总和。

实数傅里叶级数的基本表示
将函数分解为正弦曲线可以让我们更精确地分析函数,因为我们现在能够理解构成函数的底层组件。
现在,假设您有由分量 z n 表示的向量 z。

该向量可以用正交基 bn 表示,使用公式,
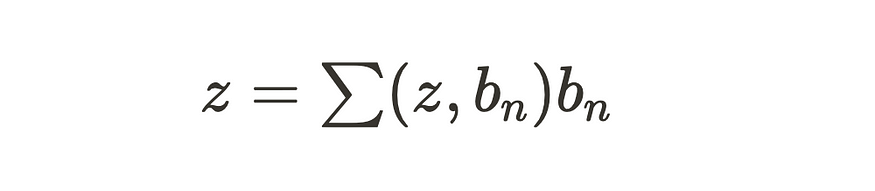
内部 (z, bn) 是 z 和基向量 bn 之间的点积。
因此,此公式可以应用于函数。
例如,假设我们有函数 f 和 g,它们的乘积是积分。这两个函数都是周期性的,周期为 T。

通过应用前面的公式,函数 f 和 g 可以重写为:

因此,实傅里叶级数允许我们使用基 bk = {fn}⋃{gn} 重写一组函数。
基函数 bn 是两组不同函数 fn 和 gn 的组合,可以写成:

其中 n ≥ 0。
因此,让我们将其应用于一个新函数。
现在假设我们有一个定义为 f 的信号。
我们可以将函数 f 重写为实傅里叶级数,并进行基数更改(如上所示)。

其中,内部系数 an 和 bn 由以下定义。
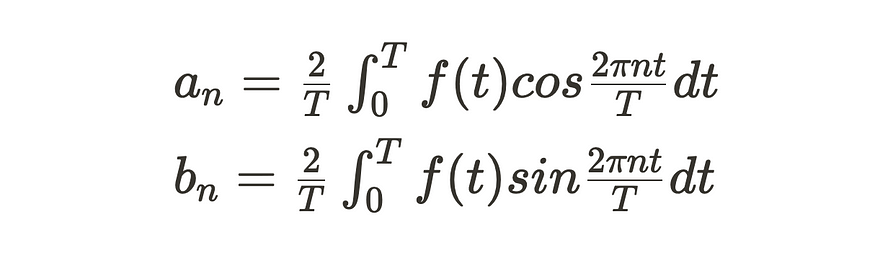
当应用于信号及其相应的频率时,n是表示频率分量的指数,t是时间,T是完整周期,系数an和bn是不同频率分量的幅度。
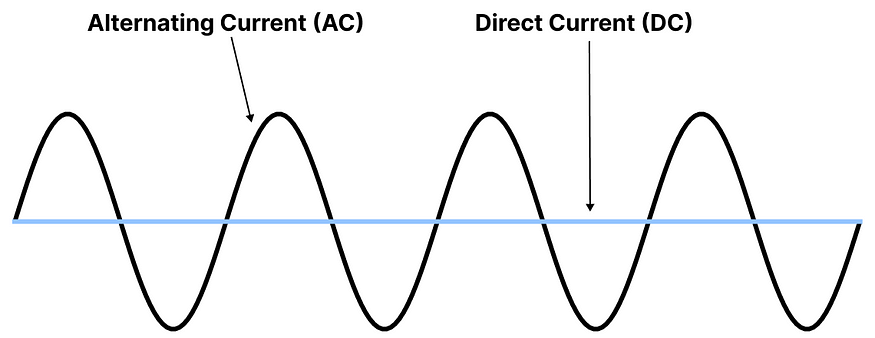
澄清一下,a₀ 不在实傅里叶级数的总和之和之外,因为它表示信号的直流 (DC) 分量。它是一个常数项,表示周期信号在一个周期内的平均值。
在实傅里叶级数中使用这个术语可以证明对于设置信号的“中心”或“基线”很有用。从那里,我们可以更有效地分析基线的交流电 (AC)。
因此,最终,实傅里叶级数是系数 a 或 bn 与正弦曲线的乘积之和。
有趣吧?
好吧,这仅仅是个开始。
四、复傅里叶级数
复傅里叶级数实际上与真正的傅里叶级数相同,至少在它们的用途上是这样。它们都旨在将周期信号表示为正弦曲线的总和。
但关键的区别在于它们如何表示信号。
复傅里叶级数不是将正弦和余弦的单独求和相加,而是在奇异复指数下表示它们。

就像这样:)
系数 an 和 bn 也可以在奇异变量 cn 下捕获。
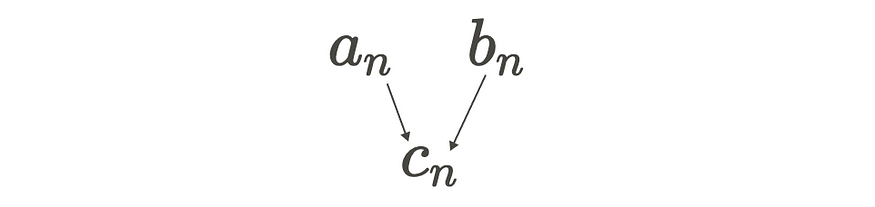
因此,复傅里叶级数是实傅里叶级数的更紧凑和简单的表示。
让我们从推导开始。
请记住,当应用于真实信号时:
n 是表示频率分量
的指数 t 是时间
T 是信号的整个周期
幸运的是,莱昂哈德·欧拉(Leonhard Euler,一位非常有趣的数学家)给了我们欧拉公式。
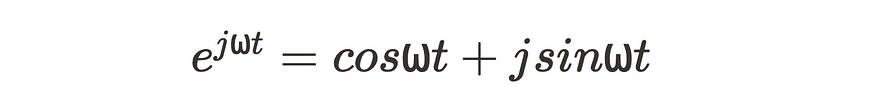
j 是虚单位。
⍵ 设置为角频率:

它基本上表示 2 个正弦曲线的总和与复指数之间的等价性。
通过欧拉公式,我们可以使用指数推导出正弦和余弦的三角恒等式。

如果你很好奇,你可以在这里查看完整的推导
因此,给定实傅里叶级数(根据 ⍵ 重写),
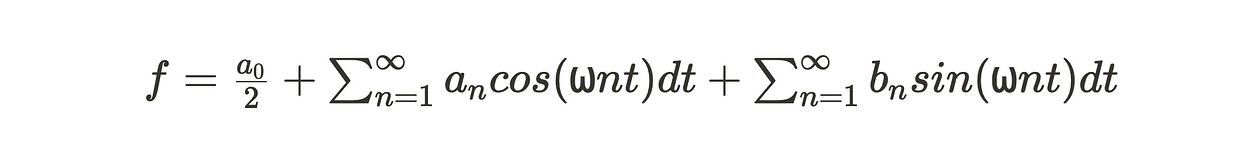
和欧拉公式,我们可以将其改写为
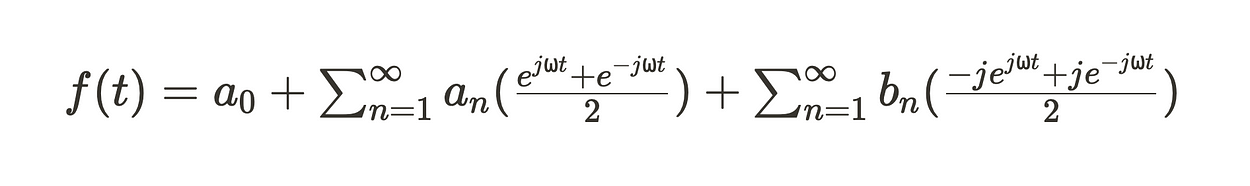
可以简化为

您可能会注意到第二个求和具有负指数。但我们希望它是一个正指数,以获得 ej⍵ⁿt 的两个求和。
因此,我们可以将 n 转换为负 n 并重写求和

现在我们有:

为了进一步简化这一点,我们可以用新的系数 cn 重写包含系数 an 和 bn 的内部表达式。

现在,系数 cn 基本上表示从 -∞ 到 ∞ 的所有可能的复系数。
因此,鉴于此,我们不需要用单独的求和来表示我们的方程。我们可以使用系数 cn 将它们连接在一个奇异求和中。
我们得到了复傅里叶级数。
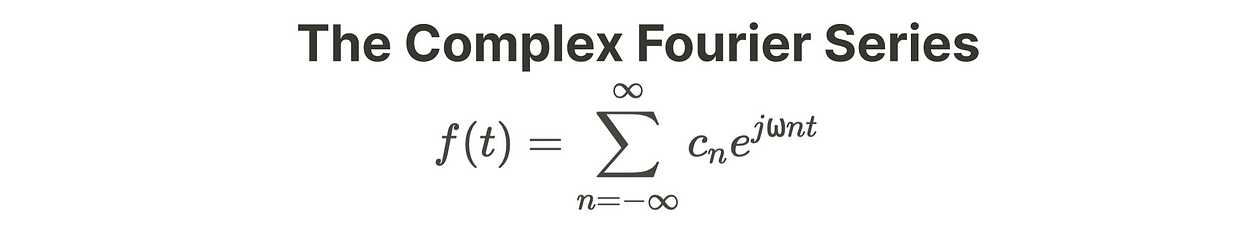
现在,系数 cn 的符号可以通过复傅里叶级数推导出来。
这种推导将允许我们找到系数 cn,而无需求解 an 和 bn。
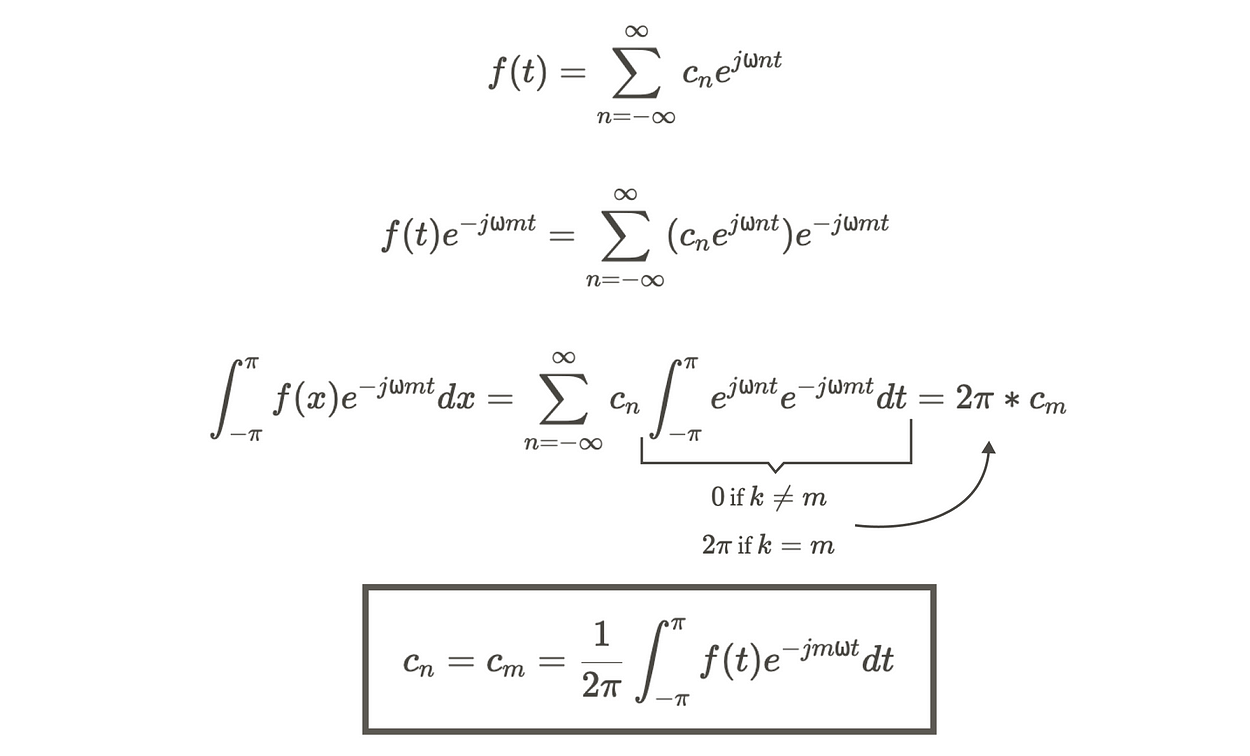
顺便说一句,我们使用 m 作为虚拟变量。它等价于 n,将其视为占位符。我们可以用 n 代替 m。
最终,作为复傅里叶级数,我们有:
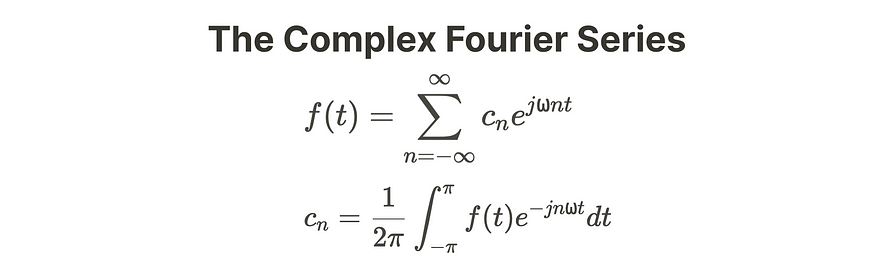
在周期 T 或 2π 上,从 -π 到 π。
快速提醒一下,除了实傅里叶级数之外,所有复傅里叶级数都是另一种将连续周期信号表示为 正弦曲线之和的方法。
区别在于使用复数指数,而且简单。
现在,进入连续傅里叶变换
五、连续傅里叶变换
到现在为止,你可能会问,“所有这些推导之间到底有什么区别?
嗯,区别在于它们如何应用以及它们可以应用于什么。
实数和复数傅里叶级数都适用于连续和周期信号。意思是长度无限大的均匀信号。

其他派生适用于不同类型的信号,例如离散信号或非周期信号。
在连续傅里叶变换的情况下,它是为连续和无限但非周期性的信号而设计的。

那么,让我们深入了解推导
让我们再看一下我们的复系数 cn。

从本质上讲,为了得到连续傅里叶变换,我们取 cn 及其无穷大的极限,将其从离散变量转换为连续变换。
因此,我们可以直接从重新排列这个方程开始,并将其极限从 -∞ 取为 ∞。

此时,在指数 e⁻⁻jw⁰ⁿt 中,⍵₀ 和 n 相乘为 ⍵,最终将系数 cn 从离散转换为连续。
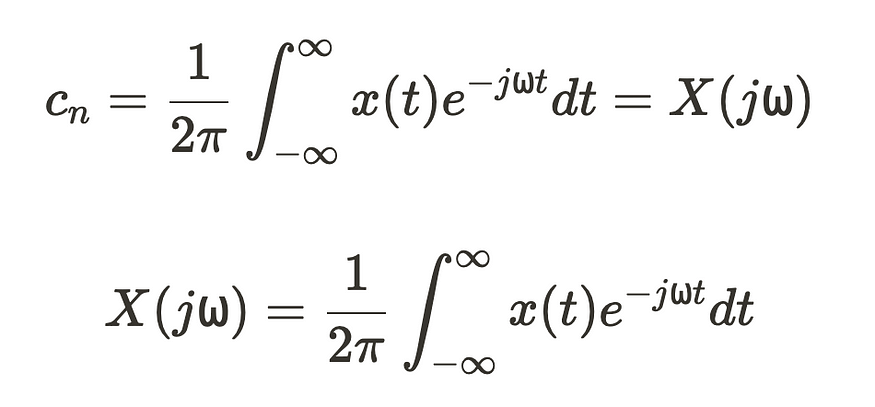
这里,x(t) 表示 f(t),因为它的极限为无穷大。X(j⍵) 是在频域中定义的信号,表征其在特定频率下的功率。
所以你有它。

从本质上讲,这种变换将连续和非周期信号x(t)从时域转换为频域X(j⍵)。
但请注意,虽然这种转换是非周期性的,并且可能看起来越来越有用......警告!
它是连续的!
在二进制 1 和 0 上运行的计算机将如何接收连续数据?
幸运的是,这就是我们有离散傅里叶变换的原因
六、离散傅里叶变换
离散傅里叶变换为使用计算机对真实数据进行采样和转换奠定了基础。
让我们以脑电图(EEG)为例。
在脑电图中,数据以特定时间间隔作为离散值输入,具体取决于采样率。鉴于此,计算机很容易处理这些数据,因为它在离散值上运行
离散傅里叶变换将允许我们使用在该脑电图中收集的离散数据,并将该数据从时域转换为频域,以便在计算机上进行更好的分析。
为了推导离散傅里叶变换,我们采用连续傅里叶变换,

并在 N 个样本的有限间隔内对其进行采样。
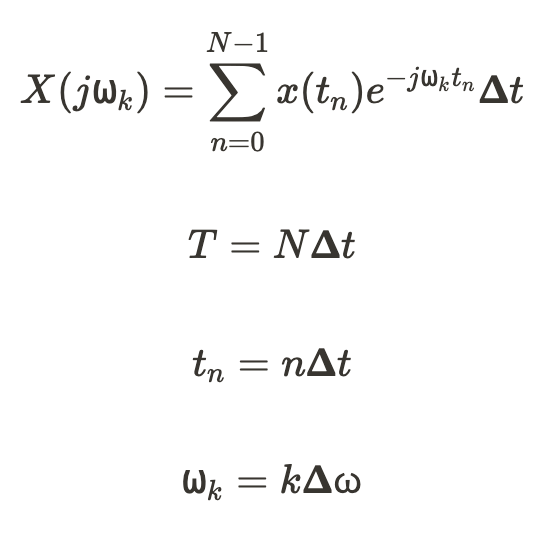
- 周期性 T 是总样本 (N) 和采样间隔 Δt 的乘积。
- 离散时间点 (tn) 是索引 n 和采样间隔 Δt 的乘积。
- ⍵,整体表示第 k 个频率分量处的频率 bin。
- ⍵k 表示 ⍵ 频率箱中第 n 个索引处的特定频率。
很酷,但 k 到底是从哪里来的???
井变量 k 表示第 k 个频率分量。在每个离散时间样本 n 处,我们将有 k 个构成信号的非周期频率分量。

不幸的是,如果我们有一个高值 N,计算机必须进行大量的计算,这可能会带来问题......我们稍后会谈到这一点。
因此,使用

我们可以将方程式改写为:
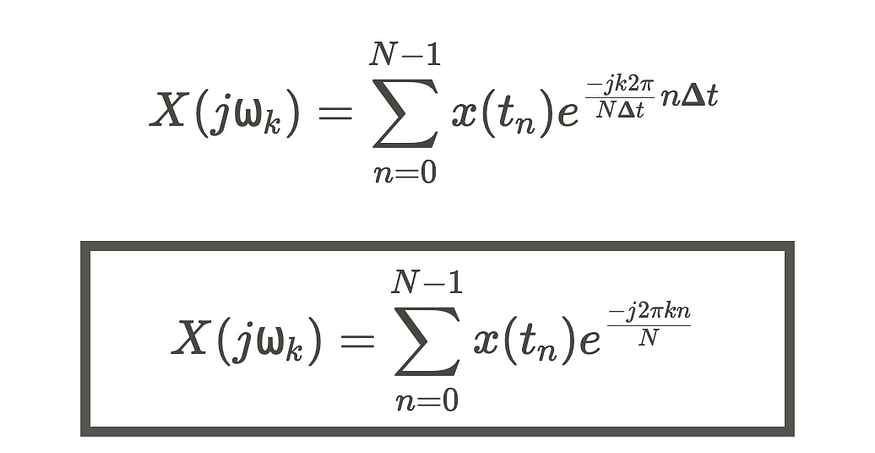
我们得到了 DFT。
但是等一下,我们还没有完成!
DFT 的方程可以简化,并通过所谓的统一根来表示。
从本质上讲,统一根是一个复数,当提高到第 n 个整数时,当 n 是正整数时,指数的结果是 1。
因此,我们可以用单位的第 N 根来表示我们的方程,
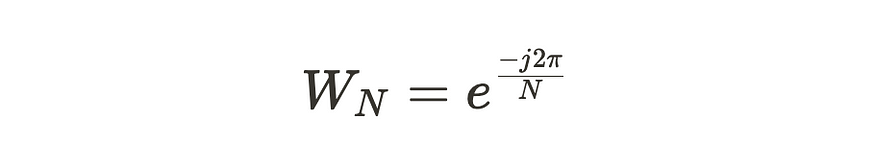
进一步简化为,
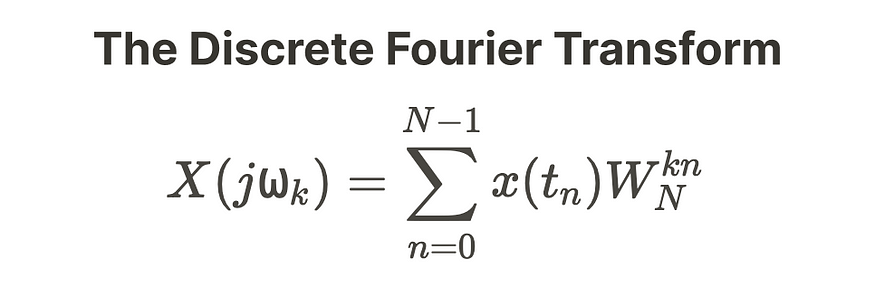
现在,如果你还记得我之前提到的,
“不幸的是,如果我们有一个高值的 N,计算机必须进行大量的计算,这可能会带来问题......我们稍后会讨论这个问题。
在计算信号的频谱/频域时,DFT可能被证明是无效的。
计算时间、负载和复杂性太多了!
原因如下。
让我们再看一下我们的DFT方程。


对于每个 k 值,我们必须处理 N-1 次计算。
如果我们再看一下早期的视觉效果,以获得更多的视角,

很明显,如果我们有一个更高的索引 N,我们将不得不处理每 N 个不断增加的 k 个计算量。
变量 N 还决定了我们的计算机将决定使用多少个索引。我们不仅要担心 k 个计算,还要担心 n。
因此,最终,当您同时考虑 k 和 n 时,您需要执行 N² 计算。
如果你听说过Big O Notation,你就会知道这很糟糕。
让我给你看看。
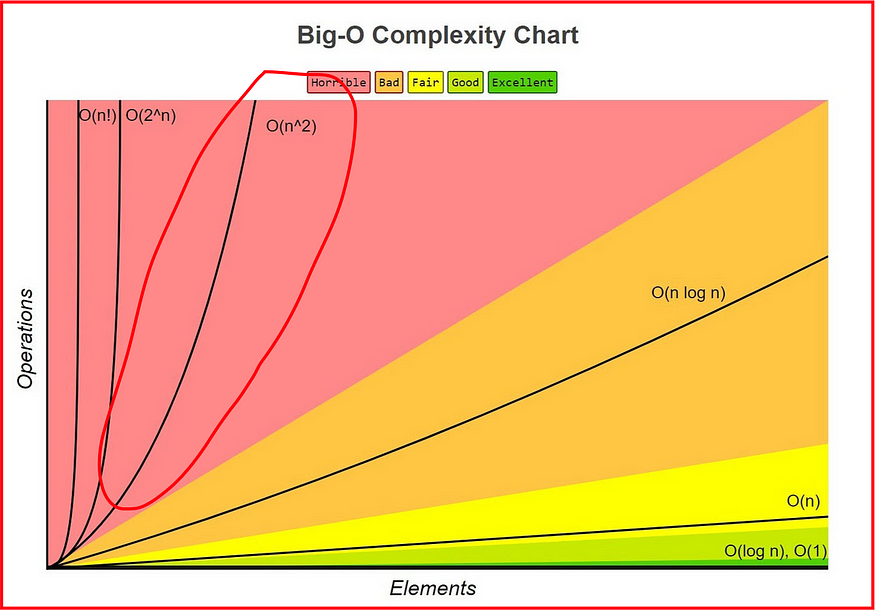
随着时间的流逝,随着我们值 N 的增加,我们的整体计算复杂度将呈指数级增长。
如果我们的数据集中有 3000 个采样数据,那么总共需要 9,000,000 次计算机操作才能遍历整个数据集。请记住,计算复杂性呈指数级增长。
与较低的 Big-O 复杂性相比,这是巨大的。
但这就是我们有快速傅里叶变换:)的原因。
七、快速傅里叶变换
因此,为了缓解 DFT 的计算复杂性随着 N 的增加呈指数级增长的问题,需要进行一些轻微的修改。
数学家约翰·图基(John Tukey)与约翰·肯尼迪(John F. Kennedy)总统进行了讨论,讨论了使用该国周围的传感器检测苏联核试验的可能性。
他意识到,为了利用这些传感器,他们需要一种计算复杂度较低的算法。
他们与James Cooley一起发表了一篇论文,概述了FFT的可用性,以便将计算复杂度从N²降低到nlog₂ n,这是一个极大的改进。

正如你所看到的,计算以更线性的方式增加,而不是指数增长。
这使得事情更加高效和可行,尤其是当我们有大量数据点需要计算时。
让我告诉你为什么。
让我们再看一下DFT。
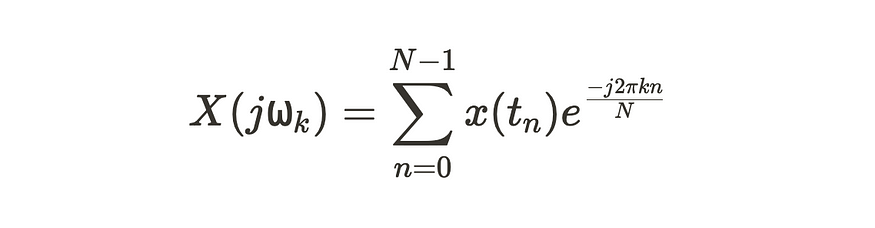
假设我们要计算第二个傅里叶系数 X(1)。

现在,假设我们还想计算第三个傅里叶系数 X(2)。
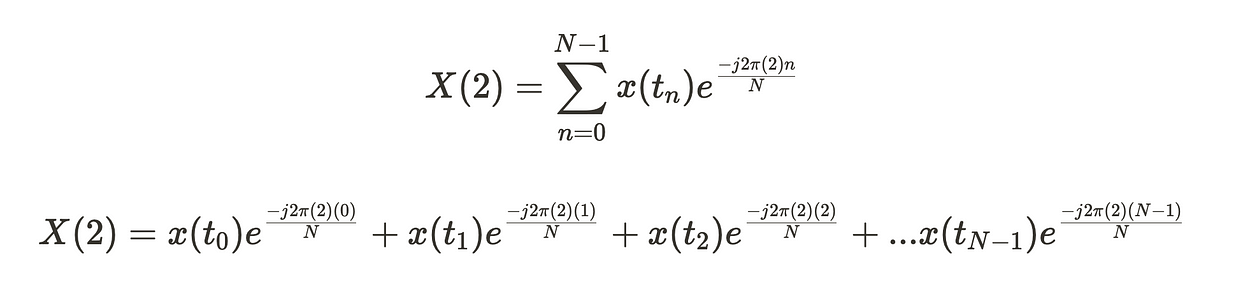
如果你没有注意到,第三个系数,其中 X(1),与第二个系数相同,其中 X(2)。

因此,最终,计算机不是计算相同的指数,在多个 k 值上两次产生相同的结果,而是使用 FFT 计算指数,然后将该指数存储在它的内存中以供将来访问。
这样可以提高计算速度并更好地利用计算资源。

DFT 矩阵
您可以看到,在 DFT 矩阵中重复 ⍵。
每个 ⍵,将仅使用 FFT 算法计算一次
在增加的 k 值上这样做,增加了每个 FFT 算法节省的计算资源量
还行。。。我们是怎么做到的?
好吧,FFT并不太复杂。将 FFT 视为一种更有效地计算 DFT 的算法。不是一个全新的公式。
让我们再看一下DFT。
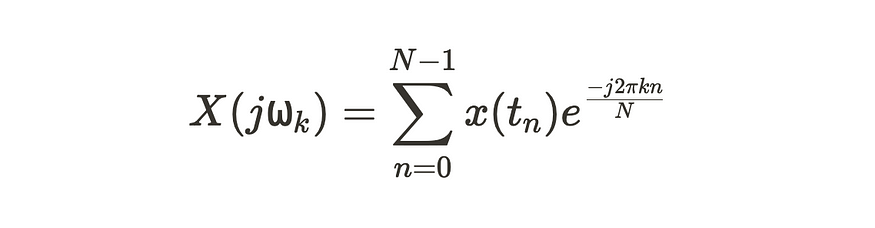
因此,这个方程可以通过除法 N/2 分为 2 个独立的序列。一个序列将包含所有偶数 n 个值,另一个序列将包含所有奇数值。
我们将序列称为 g(tn) 和 f(tn)。

鉴于此,DFT 可以分解为 2 个单独的求和。

从这里开始,我们可以进一步分解我们的求和。
让我们将下一个函数定义为 h(tn) 和 i(tn)。

每次我们将一个求和分成两个新的单独求和时,我们都会将计算 DFT 的运算总数减半。
从本质上讲,这是构成 FFT 算法的过程。
八、那又怎样
所有这些复杂的公式和算法有什么意义?所有这些转换都是我们为什么能够与复杂形式的数据进行交互的基本基础。
它是我们与之交互的各种过程和系统的重要工具,例如 X 射线、脑电图、电话、天气预报等等。
更重要的是,像这些转换这样的基础数学为创造新的和改进的技术让路,如脑机接口、量子计算、智能电网,甚至人工智能。

了解新兴技术背后的数学过程可以让您真正了解如何开始使用它们甚至改进它们。
相关文章:

傅立叶之美:深入研究傅里叶分析背后的原理和数学
一、说明 T傅里叶级数及其伴随的推导是数学在现实世界中最迷人的应用之一。我一直主张通过理解数学来理解我们周围的世界。从使用线性代数设计神经网络,从混沌理论理解太阳系,到弦理论理解宇宙的基本组成部分,数学无处不在。 当然,…...
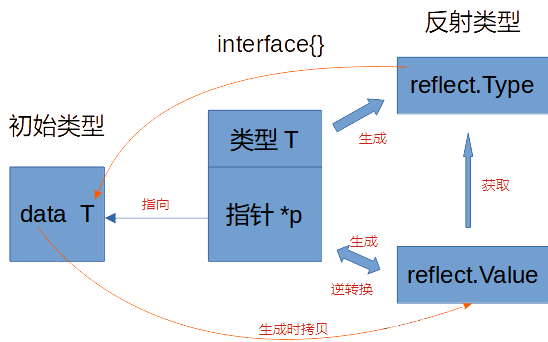
golang学习随便记16-反射
为什么需要反射 下面的例子中编写一个 Sprint 函数,只有1个参数(类型不定),返回和 fmt.Fprintf 类似的格式化后的字符串。实现方法大致为:如果参数类型本身实现了 String() 方法,那调用 String() 方法即可…...

识别恶意IP地址的有效方法
在互联网的环境中,恶意IP地址可能会对网络安全造成严重威胁,例如发起网络攻击、传播恶意软件等。因此,识别恶意IP地址是保护网络安全的重要一环。IP数据云将探讨一些有效的方法来识别恶意IP地址。 IP地址查询:https://www.ipdata…...

探索信号处理:低通滤波器的原理与应用
在信号处理领域,滤波器的应用至关重要,它能够帮助我们从复杂的信号中提取需要的信息,而低通滤波器则是其中一种被广泛应用的滤波器类型。本文旨在深入探讨低通滤波器的基本原理、主要类型以及在实际应用中的作用和实现方式。 ### 1. 低通滤波…...
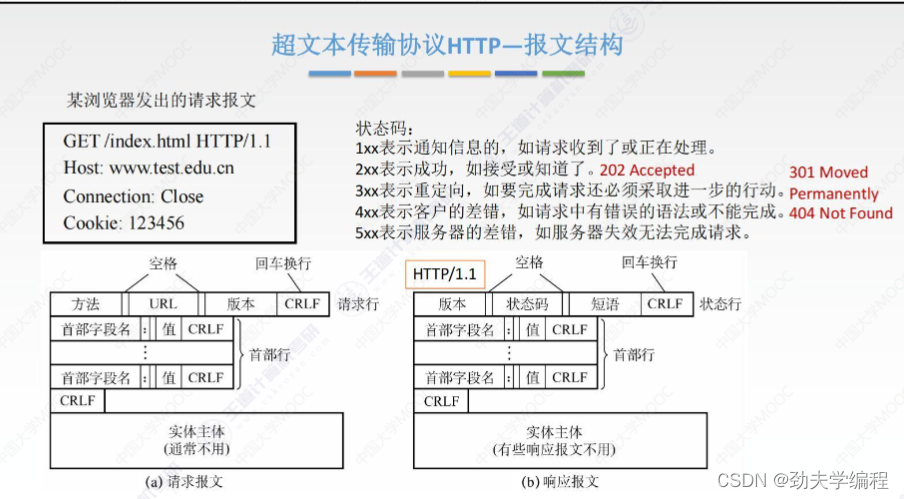
计算机网络:应用层知识点汇总
文章目录 一、网络应用模型二、域名系统(DNS)三、文本传输协议(FTP)四、电子邮件五、万维网和HTTP协议 一、网络应用模型 p2p也就是对等模型 二、域名系统(DNS) 我们知道,随着人们建立一个网站…...
金三银四!一个年薪160W+的就业方向!
前言 随着越来越多的科技大厂加入鸿蒙生态建设,鸿蒙开发人才正在市场上被争抢。资深工程师开出的年薪高达近百万,架构师更是高至160万,真可谓“鸿蒙猿年薪超百万”。如何抓住新技术红利,尽早上车?你会成为下一个鸿蒙开…...
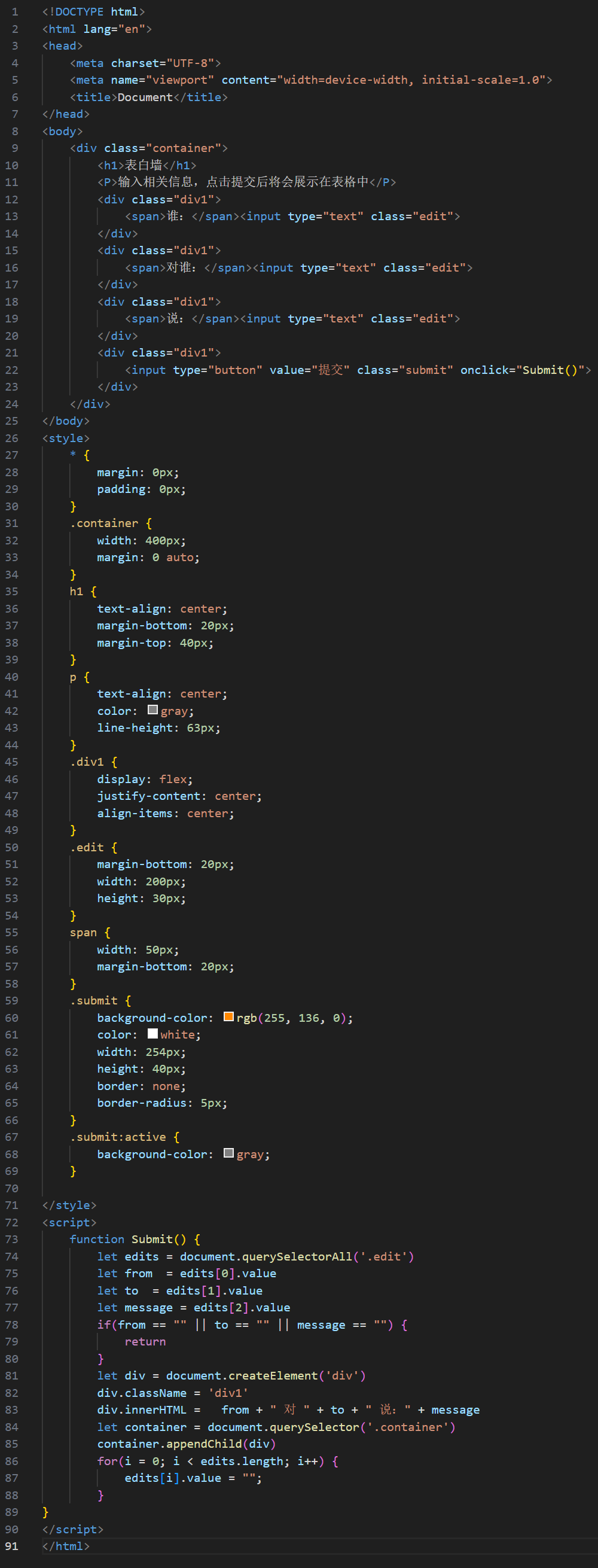
实现的一个网页版的简易表白墙
实现的一个网页版的表白墙 实现效果 代码截图 相关代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><tit…...

随身WiFi靠谱吗? 看完这篇文章你就懂了?2024随身wifi靠谱品牌推荐
在网络如此发达,随身WiFi如此普遍的2024年,仍有人在质疑随身WiFi到底靠不靠谱,有没有用处。其实只需要回答两个问题: 1、你的流量够用吗?手机的流量包和随身WiFi套餐哪个更便宜? 2、手机流量不够用&#x…...

mysql的trace追踪SQL工具,进行sql优化
trace是MySQL5.6版本后提供的SQL跟踪工具,通过使用trace可以让我们明白optimizer(优化器)如何选择执行计划。 注意:开启trace工具会影响mysql性能,所以只适合临时分析sql使用,用完之后请立即关闭。 测试数…...
docker部署springboot jar包项目
docker部署springboot jar包项目 前提,服务器环境是docker环境,如果服务器没有安装docker,可以先安装docker环境。 各个环境安装docker: Ubuntu上安装Docker: ubuntu离线安装docker: CentOS7离线安装Docker࿱…...
一个八年工作经验老程序员的分享
作为一个 Java 程序员,我在这个行业中工作了多年。在这个过程中,我经历了许多挑战和机遇,也学到了很多宝贵的经验和教训。在这篇文章中,我想分享一些我的感想和思考,希望能够对其他 Java 程序员有所帮助。 一、技术的…...

代码随想录算法训练营第四十三天|动态规划|1049. 最后一块石头的重量 II、494. 目标和、474.一和零
1049. 最后一块石头的重量 II 文章 有一堆石头,每块石头的重量都是正整数。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果如下: 如果 x y&a…...
vue3+elementPlus:el-table-column表格列动态设置单元格颜色
:cell-style属性 //html<el-tableempty-text"暂无数据":data"datalist.table":max-height"height"row-key"id"border:cell-style"cellStyle"> <el-table>//js //动态设置单元格颜色 const cellStyle ({ row, c…...

python和shell脚本,每隔五分钟将远端服务器中的文件夹数据下载到跳板机
python脚本 import subprocess import datetime import timedef run_scp_command(source_path, target_path):command [scp -r , source_path, target_path]try:subprocess.run(command, checkTrue)print("File transferred successfully!")except subprocess.Call…...
Websocket在Asp.net webApi(.net framework)上的应用
之前在写看板部分的web api的时候,都是通过Ajax在规定时间内轮询调用web api,这样简单省事,但是当看板多了(并发量上来)以后,比较消耗服务器的性能,所以最近研究了websocket,希望使用…...
App前端开发跨平台框架比较:React Native、Flutter、Xamarin等
引言 移动应用开发领域的跨平台框架正在不断演进,为开发者提供更多选择。在本文中,我们将比较几个流行的跨平台框架:React Native、Flutter和Xamarin等。讨论它们的优缺点、适用场景以及开发体验。 第一部分 React Native: 优缺点、适用场景…...

VR数字展厅在企业中应用的优势有哪些?
随着VR全景技术的成熟,VR数字展厅逐渐成为了企业展示形象和产品的重要手段之一。VR企业数字展厅是一种通过VR技术、3D建模技术展示企业形象和产品的创新方式,将企业线下的展厅搬到线上,为企业品牌形象带来了很多优势。 VR数字展厅在企业中应用…...

【数据库】索引 视图 触发器 分页查询
目录 1、索引 2、视图 3、触发器 4、分页查询⚠️ 1、索引 提升查询效率、当数据量小的时候,索引看不出来效果,当数据量很大的时候,索引会显著提高查询速度 当给表添加索引之后,新插入一条数据,就会让索引进行重新…...
*地宫取宝c++
题目 输入样例1: 2 2 2 1 2 2 1输出样例1: 2输入样例2: 2 3 2 1 2 3 2 1 5输出样例2: 14 思路 题目说从入口开始,只能向右或向下行走到达右下角,类似“摘花生”这道题的模型。题目又说只有当格子里的宝…...
同态滤波算法详解
同态滤波是一种用于增强图像的方法,特别适用于去除图像中的照明不均和阴影。该算法基于照射反射模型,将图像分解为两个分量:照射分量(illumination component)和反射分量(reflection component)…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
