代码随想录算法训练营第四十三天|动态规划|1049. 最后一块石头的重量 II、494. 目标和、474.一和零
1049. 最后一块石头的重量 II
文章
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
示例:
输入:[2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
提示:
1 <= stones.length <= 30
1 <= stones[i] <= 1000
和416. 分割等和子集 (opens new window)非常像了,尽可能平均分。
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {vector<int> dp(15001, 0);int sum = 0;for (int i = 0; i < stones.size(); i++) sum += stones[i];int target = sum / 2;for (int i = 0; i < stones.size(); i++) { // 遍历物品for (int j = target; j >= stones[i]; j--) { // 遍历背包dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - dp[target] - dp[target];}
};
494. 目标和
文章
给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
输入:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
提示:
数组非空,且长度不会超过 20 。
初始的数组的和不会超过 1000 。
保证返回的最终结果能被 32 位整数存下。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
所有元素凑成left有多少种方法 组合问题
dp[i][j] dp1-i凑成j的方法个数
dp[i][j]=dp[i-1][j-nums[i]]+dp[i-1][j]
一维:dp[j]=dp[j-nums[i]+dp[j] 注意从后往前
注意这种情况: bagSize = (S + sum) / 2 小于0 此时 没有结果。
class Solution {
public:int findTargetSumWays(vector<int>& nums, int S) {int sum = 0;for (int i = 0; i < nums.size(); i++) sum += nums[i];if (abs(S) > sum) return 0; // 此时没有方案if ((S + sum) % 2 == 1) return 0; // 此时没有方案int bagSize = (S + sum) / 2;vector<int> dp(bagSize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
};
474.一和零
文章讲解
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。 其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = [“10”, “0”, “1”], m = 1, n = 1
输出:2
解释:最大的子集是 {“0”, “1”} ,所以答案是 2 。
提示:
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100
题目的关键是将0和1拆解开
dp[i] [jm] [jn]=max( dp[i-1] [jm-nums0[i]] [jn-nums1[i]] +1 , dp[i-1] [jm] [jn]
初始化:0
从后往前
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(auto str:strs){int num1=0;int num0=0;for(auto c :str){if (c == '0') num0++;else num1++;}for(int i=m;i>=num0;i--){for(int j=n;j>=num1;j--){dp[i][j]=max(dp[i][j],dp[i-num0][j-num1]+1);}}}return dp[m][n];}
};
相关文章:

代码随想录算法训练营第四十三天|动态规划|1049. 最后一块石头的重量 II、494. 目标和、474.一和零
1049. 最后一块石头的重量 II 文章 有一堆石头,每块石头的重量都是正整数。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果如下: 如果 x y&a…...
vue3+elementPlus:el-table-column表格列动态设置单元格颜色
:cell-style属性 //html<el-tableempty-text"暂无数据":data"datalist.table":max-height"height"row-key"id"border:cell-style"cellStyle"> <el-table>//js //动态设置单元格颜色 const cellStyle ({ row, c…...

python和shell脚本,每隔五分钟将远端服务器中的文件夹数据下载到跳板机
python脚本 import subprocess import datetime import timedef run_scp_command(source_path, target_path):command [scp -r , source_path, target_path]try:subprocess.run(command, checkTrue)print("File transferred successfully!")except subprocess.Call…...
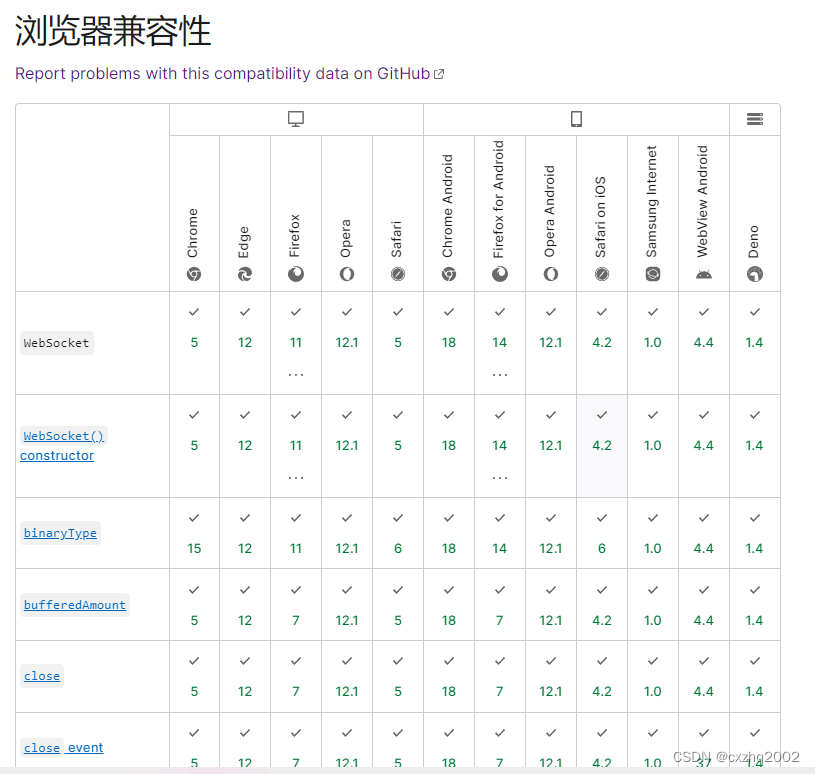
Websocket在Asp.net webApi(.net framework)上的应用
之前在写看板部分的web api的时候,都是通过Ajax在规定时间内轮询调用web api,这样简单省事,但是当看板多了(并发量上来)以后,比较消耗服务器的性能,所以最近研究了websocket,希望使用…...
App前端开发跨平台框架比较:React Native、Flutter、Xamarin等
引言 移动应用开发领域的跨平台框架正在不断演进,为开发者提供更多选择。在本文中,我们将比较几个流行的跨平台框架:React Native、Flutter和Xamarin等。讨论它们的优缺点、适用场景以及开发体验。 第一部分 React Native: 优缺点、适用场景…...

VR数字展厅在企业中应用的优势有哪些?
随着VR全景技术的成熟,VR数字展厅逐渐成为了企业展示形象和产品的重要手段之一。VR企业数字展厅是一种通过VR技术、3D建模技术展示企业形象和产品的创新方式,将企业线下的展厅搬到线上,为企业品牌形象带来了很多优势。 VR数字展厅在企业中应用…...

【数据库】索引 视图 触发器 分页查询
目录 1、索引 2、视图 3、触发器 4、分页查询⚠️ 1、索引 提升查询效率、当数据量小的时候,索引看不出来效果,当数据量很大的时候,索引会显著提高查询速度 当给表添加索引之后,新插入一条数据,就会让索引进行重新…...
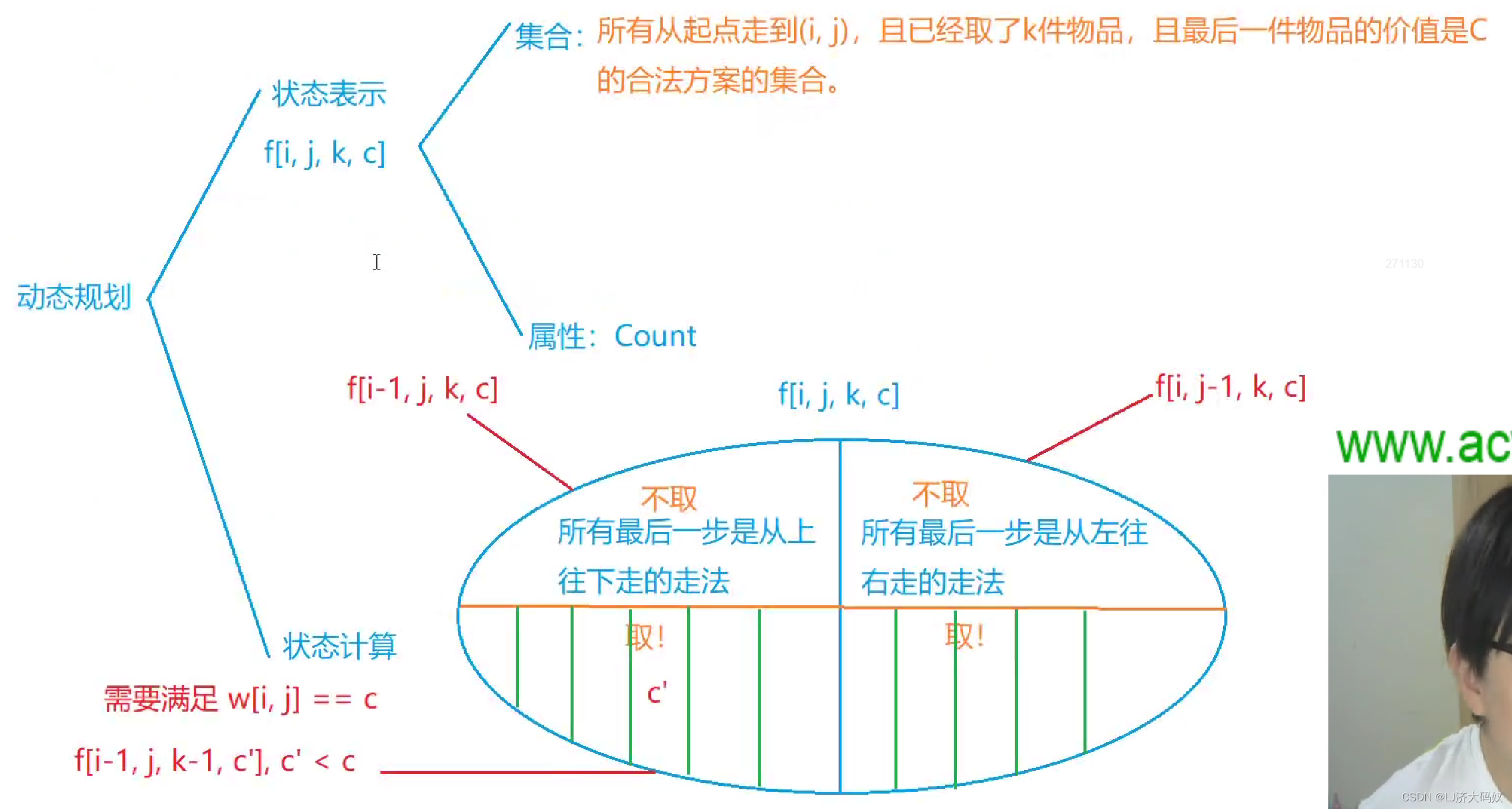
*地宫取宝c++
题目 输入样例1: 2 2 2 1 2 2 1输出样例1: 2输入样例2: 2 3 2 1 2 3 2 1 5输出样例2: 14 思路 题目说从入口开始,只能向右或向下行走到达右下角,类似“摘花生”这道题的模型。题目又说只有当格子里的宝…...
同态滤波算法详解
同态滤波是一种用于增强图像的方法,特别适用于去除图像中的照明不均和阴影。该算法基于照射反射模型,将图像分解为两个分量:照射分量(illumination component)和反射分量(reflection component)…...

财务管理系统报账和挂账分别什么区别!报销又是什么【第三期】
前言 已经写了两期 财务管理系统之saas多租户架构是什么以及分库分表以及如何选择分布式事务方案 【程序员聊业务】财务管理系统之模块分类 报账和挂账概念 报账是指企业或个人因业务需要而发生的各项费用支出,在支付后,需要将相关的票据、凭证等提交…...

最少刷题数
最少刷题数 题目分析 对于每一名同学计算还需要再刷多少题才能保证刷题数比他多的人数不超过刷题数比他少的学生人数。我们可以考虑统计每一个分数的前缀和数组,sum[i]表示当前学生中,刷题数小于等于i的人数。那么对于学生i的刷题数a[i],su…...

Python刘诗诗
写在前面 刘诗诗在电视剧《一念关山》中饰演了女主角任如意,这是一个极具魅力的女性角色,她既是一位有着高超武艺和智慧的女侠士,也曾经是安国朱衣卫前左使,身怀绝技且性格坚韧不屈。剧中,任如意因不满于朱衣卫的暴行…...

探索ChatGPT在软件架构师工作中的应用
随着人工智能技术的不断发展,自然语言处理模型如OpenAI的ChatGPT已经成为了解决各种实际问题的强大工具之一。在软件架构师这个领域,ChatGPT也有着广泛的应用。本文将探讨软件架构师如何有效地利用ChatGPT来解决问题和提高工作效率。 ChatGPT简介 Chat…...

pytest--allure报告中添加用例详情
前言 前面介绍了如何生成allure的报告,看着allure的页面非常好看,但是感觉少了一些内容,allure还可以增加一些用例详情内容,这样让我们的报告看着更加绚丽。 allure增加用例详情 我们可以在报告测试套件中增加用例详情内容。 …...

【深度学习笔记】9_5 多尺度目标检测
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 9.5 多尺度目标检测 在9.4节(锚框)中,我们在实验中以输入图像的每个像素为中心生成多个锚框。这些…...
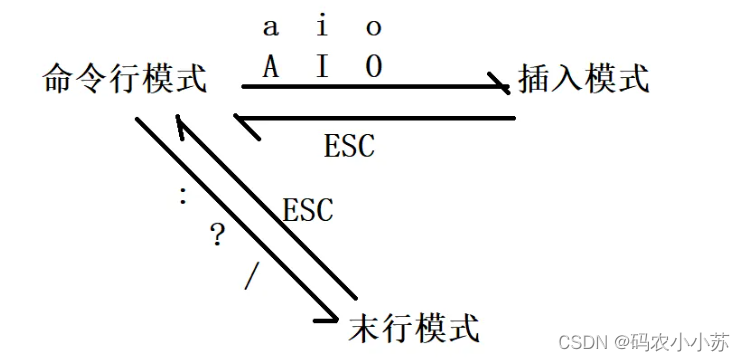
Linux--vim
一.什么是vim Vim(Vi IMproved)是一种文本编辑器,通常在Linux和其他类Unix操作系统中使用。它是Vi编辑器的增强版本,提供了更多的功能和定制选项。Vim具有强大的文本编辑和编程功能,支持语法高亮、代码折叠、宏录制、…...
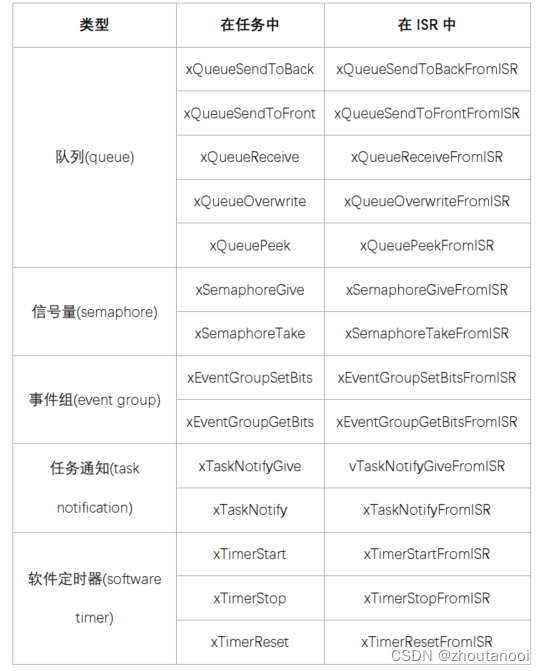
FreeRTOS操作系统学习——中断管理
中断管理介绍 嵌入式实时系统需要对整个系统环境产生的事件作出反应。这些事件对处理时间和响应时间都有不同的要求。事件通常采用中断方式检测,中断服务例程(ISR)中的处理量应当越短越好。ISR是在内核中被调用的, ISR执行过程中,用户的任务…...
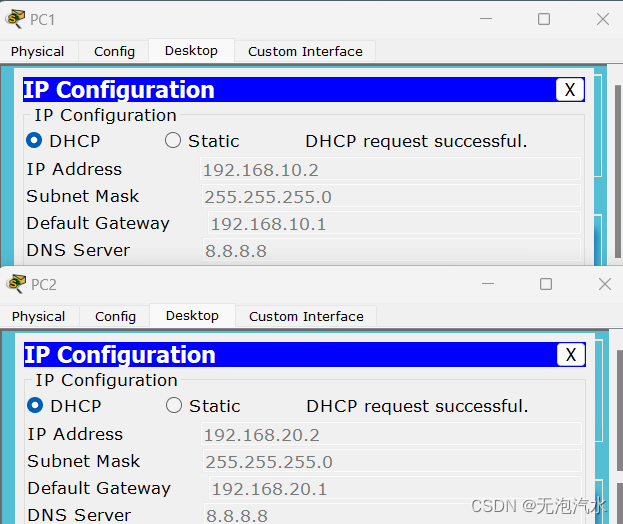
DHCP中继实验(思科)
华为设备参考:DHCP中继实验(华为) 一,技术简介 DHCP中继,可以实现在不同子网和物理网段之间处理和转发DHCP信息的功能。如果DHCP客户机与DHCP服务器在同一个物理网段,则客户机可以正确地获得动态分配的IP…...
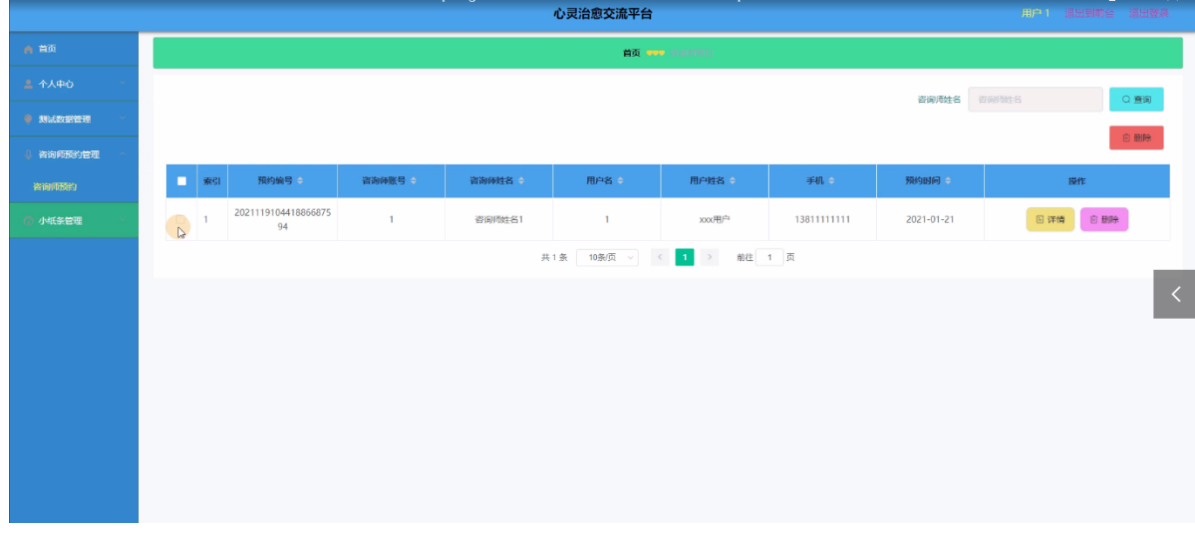
基于SpringBoot的“心灵治愈交流平台”的设计与实现(源码+数据库+文档+PPT)
基于SpringBoot的“心灵治愈交流平台”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:SpringBoot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统功能界面图 登录、用户注册界面图 心灵专…...
【SpringBoot】自定义工具类实现Excel数据新建表存入MySQL数据库
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》《项目实战》 🛸学无止境,不骄不躁,知行合一 文章目录 …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
