数据结构:堆
堆的概念
1.堆是一个完全二叉树
2.小堆(任何一个父亲<=孩子),大堆(任何一个父亲>=孩子)
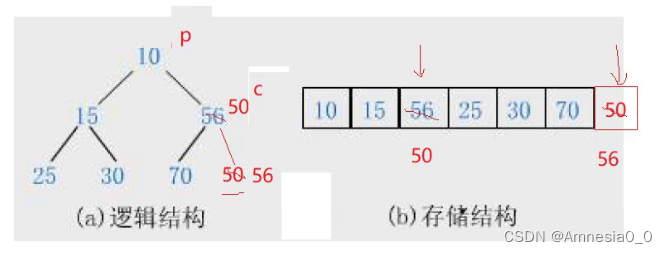
堆的结构
物理结构:数组
逻辑结构:二叉树
#pragma once
#include<assert.h>
#include<iostream>
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的构建
void HeapInit(Heap* hp);
void HeapInitArray(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);
#include"标头.h"
void HeapInit(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}void HeapInitArray(Heap* hp, HPDataType* a, int n)// 一次性初始化堆,插入所有值
{assert(hp);hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);memcpy(hp->_a, a, sizeof(HPDataType) * n);
//第一个节点不用调,时间复杂度为O(n*logn)//for (int i = 1; i < n; i++)//向上调整建堆//{// AdjustUp(hp->_a, i);//}
//叶节点不用调(没有子节点),时间复杂度为O(N)for (int i = (hp->_size-1 - 1) / 2; i >= 0; i--)//向下调整建堆//(hp->_size-1 - 1) / 2第一个-1是下标,后面的-1和/2是求父节点的公式{AdjustDown(hp->_a, hp->_size, i);}
}void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}void Swap(HPDataType* px, HPDataType* py)
{HPDataType temp = *px;*px = *py;*py = temp;
}
void AdjustUp(HPDataType* a, int child)//向上调整数据,是它成小堆/大堆
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_size == hp->_capacity){size_t newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* temp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (temp == NULL){perror("realloc fail");return;}hp->_a = temp;hp->_capacity = newcapacity;}hp->_a[hp->_size] = x;hp->_size++;AdjustUp(hp->_a, hp->_size - 1);
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//假设法选出小的孩子while (child < n){if (a[child + 1] < a[child] && child + 1 < n){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HeapPop(Heap* hp)//删除堆顶的数据
{assert(hp);assert(hp->_size > 0);//不可以挪动覆盖来删除堆顶数据//问题1.挪动覆盖时间复杂度O(N)// 2.堆结构被破坏,父子变兄弟,兄弟变父子//因此可以将首尾数据交换,删除尾部数据,然后进行向下调整算法Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjustDown(hp->_a, hp->_size, 0);
}HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}堆排序
堆排序的本质是利用堆的性质,取出堆顶的数(最大或最小),然后将堆顶换成第二小/大的数
void HpSort(HPDataType* a, int n)
{Heap hp;HeapInitArray(&hp, a, n);int i = 0;while (!HeapEmpty(&hp)){a[i++] = HeapTop(&hp);HeapPop(&hp);}HeapDestory(&hp);
}当然,这样的排序存在一定的缺点:
1.空间复杂度为O(N),太大了
2.使用是需要有堆这个数据结构
为了节省空间,可以通过将原数组改造成堆来排序,
排列出升序的数组采取堆排序应当使用大堆,因为小堆的堆顶是最小的数,堆顶的数已经是最小的了,不能改了
因此需要其他的数重新组成一个新堆,但是原本的堆全部乱了,父子变兄弟等问题会出现,只能重新建堆,浪费了时间因此需要采用大堆
大堆的堆顶是最大的,因此可以进行首尾交换,最大值就在数组尾部了,然后不把最后一个数看作堆内的数,继续进行向下调整,就可以选出次大的数
//创建大堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//假设法选出小的孩子while (child < n){if (a[child + 1] > a[child] && child + 1 < n){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HpSort(HPDataType* a, int n)
{//先将数组建堆,时间复杂度O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i)//调整叶子上一层(叶子(最后面)在最后,不需要调整){AdjustDown(a, n, i);}//int end = n - 1;//end为数组下标while (end > 0){Swap(&a[0], &a[end]);//交换首尾AdjustDown(a, end, 0);//将堆首下调--end;}
}int main()
{int a[9] = { 9,8,7,6,5,4,3,2,1 };HeapSort(a, 9);for (int i = 0; i < 9; i++){printf("%d ", a[i]);}return 0;
}
这样,一个简单的堆排序就完成了
相关文章:

数据结构:堆
堆的概念 1.堆是一个完全二叉树 2.小堆(任何一个父亲<孩子),大堆(任何一个父亲>孩子) 堆的结构 物理结构:数组 逻辑结构:二叉树 #pragma once #include<assert.h> #include<iostream> typedef int HPDataType; typedef struct Heap {HPDataType* _a;int…...

CSS中三栏布局的实现
三栏布局一般指的是页面中一共有三栏,左右两栏宽度固定,中间自适应的布局,三栏布局的具体实现: 利用绝对定位,左右两栏设置为绝对定位,中间设置对应方向大小的margin的值。 .outer {position: relative;h…...
Linux搭建我的世界(MC)整合包服务器,All the Mods 9(ATM9)整合包开服教程
Linux使用MCSM面板搭建我的世界(Minecraft)整合包服务器,MC开服教程,All the Mods 9(ATM9)整合包搭建服务器的教程。 本教程使用Docker来运行mc服,可以方便切换不同Java版本,方便安装多个mc服版本。 视频教程:https:…...

让数据在业务间高效流转,镜舟科技与NineData完成产品兼容互认
近日,镜舟科技与NineData完成产品兼容测试。在经过联合测试后,镜舟科技旗下产品与NineData云原生智能数据管理平台完全兼容,整体运行高效稳定。 镜舟科技致力于帮助中国企业构建卓越的数据分析系统,打造独具竞争力的“数据护城河”…...
2.1HTML5基本结构
HTML5实际上不算是一种编程语言,而是一种标记语言。HTML5文件是由一系列成对出现的元素标签嵌套组合而成,这些标签以<元素名>的形式出现,用于标记文本内容的含义。浏览器通过元素标签解析文本内容并将结果显示在网页上,而元…...

设置浏览器显示小于12px以下字体
问题 我们在项目开发过程中有时候会遇到设计师给的小于12px的字体,IE、火狐浏览器、移动端等小于12px的字号大小还是可以正常显示的,但是谷歌浏览器上显示字体最小为12px,css设置font-size:10px,运行代码显示结果仍然…...

web蓝桥杯真题:成语学习
代码: //TODO 点击文字后,在idiom从左到右第一个空的位置加上改文字 getSingleWord(val) {let index this.idiom.indexOf() //从左往右查询空字符串this.$set(this.idiom, index, val) //响应式更新 },// TODO 校验成语是否输入正确答案 confirm…...

外包干了5天,技术明显退步。。。。。
先说一下自己的情况,本科生,19年通过校招进入南京某软件公司,干了接近2年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了2年的功能测试&…...

Vue:自定义消息通知组件
一、效果描述 在JS中使用一个Message函数,弹出一个自定义的消息框。 效果体验:缓若江海凝清光 二、实现方式 1.新建一个消息组件 2.新建一个js文件,新建一个需要导出函数 3.在函数中新建一个Vue实例,并将消息组件挂载上去。…...

2023 收入最高的十大编程语言
本期共享的是 —— 地球上目前已知超过 200 种可用的编程语言,了解哪些语言在 2023 为开发者提供更高的薪水至关重要。 过去一年里,我分析了来自地球各地超过 1000 万个开发职位空缺,辅助我们了解市场,以及人气最高和收入最高的语…...

Github 2024-03-11 开源项目周报 Top15
根据Github Trendings的统计,本周(2024-03-11统计)共有15个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目4TypeScript项目3Jupyter Notebook项目3C#项目1HTML项目1CSS项目1Dart项目1Lua项目1Shell项目1Rust…...
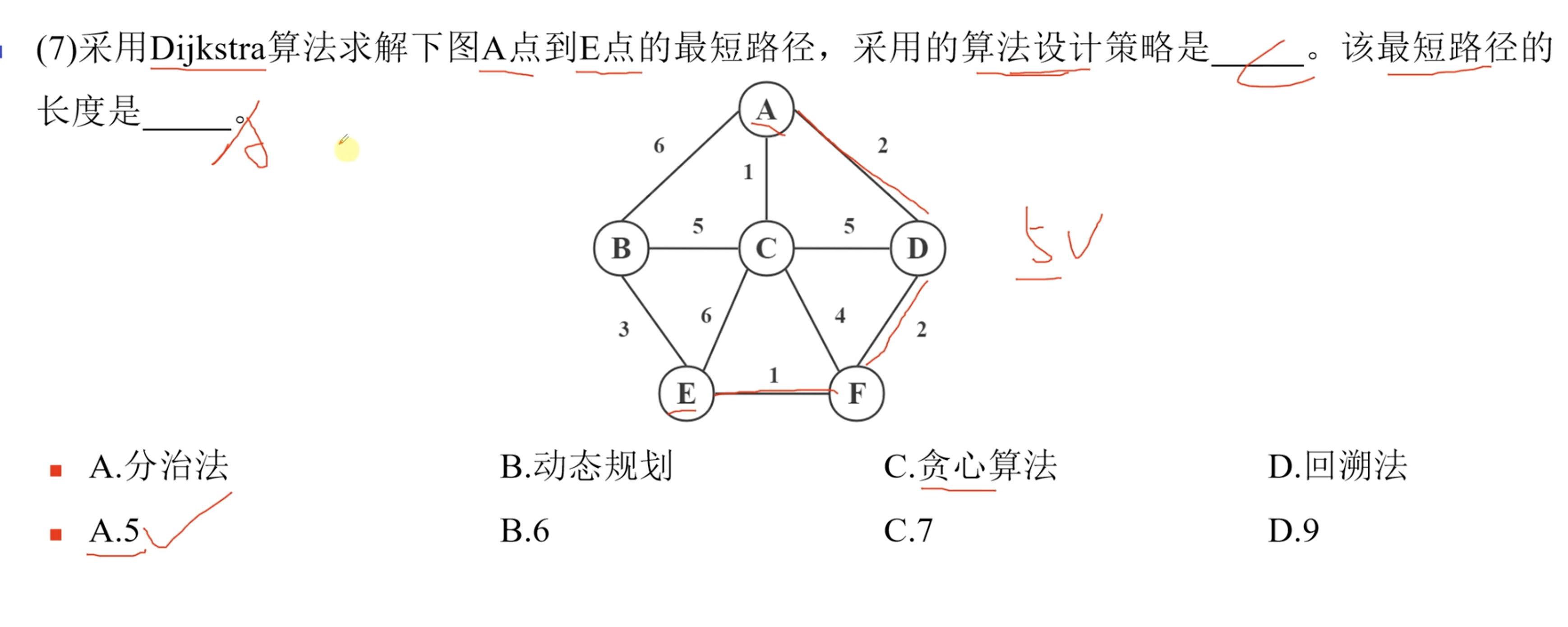
【DAY10 软考中级备考笔记】数据结构 图
数据结构 图 3月11日 – 天气:晴 晚上无线网络突然不能用了,花费好久弄这个,耽误了一些时间 1. 图的定义 这里需要注意完全图的定义,以及完全图的边数 这里需要注意连通图和连通分量的概念。 2. 图的存储结构 图有两种存储结构&a…...
java-ssm-jsp基于java的餐厅点餐系统的设计与实现
java-ssm-jsp基于java的餐厅点餐系统的设计与实现 获取源码——》公主号:计算机专业毕设大全...

蓝桥杯(1):python排序
1 基础 1.1 输出 1.1.1 去掉输出的空格 print("Hello","World",123,sep"") print("hello",world,123,sep) print(hello,world,123) #输出结果 #HelloWorld123 #helloworld123 #hello world 123 1.1.2 以不同的方式结尾 print(&quo…...
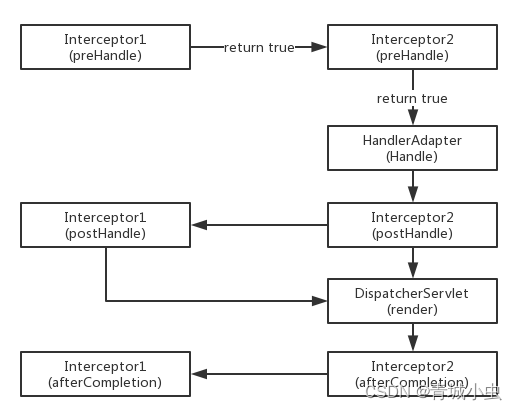
SpringMVC请求、响应和拦截器的使用
SpringMVC请求 RequestMapping注解 RequestMapping注解的作用是建立请求URL和处理方法之间的对应关系 RequestMapping注解可以作用在方法和类上 1. 作用在类上:第一级的访问目录 2. 作用在方法上:第二级的访问目录 3. 细节:路径可以不编写…...
基于springboot+layui仓库管理系统设计和实现
基于 java springbootlayui仓库管理系统设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取…...
【开源-土拨鼠充电系统】鸿蒙 HarmonyOS 4.0+微信小程序+云平台
本人自己开发的开源项目:土拨鼠充电系统 ✍GitHub开源项目地址👉:https://github.com/cheinlu/groundhog-charging-system ✍Gitee开源项目地址👉:https://gitee.com/cheinlu/groundhog-charging-system ✨踩坑不易&am…...

[抽象]工厂模式([Abstract] Factory)——创建型模式
[抽象]工厂模式——创建型模式 什么是抽象工厂? 抽象工厂模式是一种创建型设计模式,让你能够保证在客户端程序中创建一系列有依赖的对象组时,无需关心这些对象的类型。 具体来说: 对象的创建与使用分离: 抽象工厂模…...
QT网络编程之实现UDP广播发送和接收
推荐一个不错的人工智能学习网站,通俗易懂,内容全面,作为入门科普和学习提升都不错,分享一下给大家:前言https://www.captainbed.cn/ai 一.UDP通信 1.QT中实现UDP通信主要用到了以下类:QUdpSocket、QHost…...
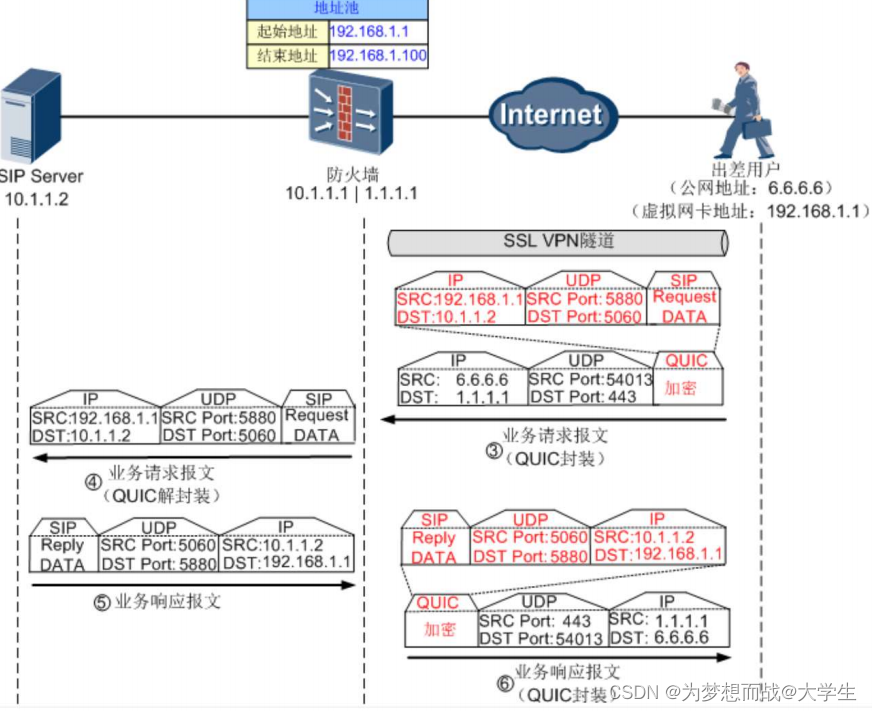
SSL VPN基础原理
目录 SSL ---安全传输协议(安全套接层)---TLS ----传输层安全协议 SSL的工作原理 SSL会话建立的过程 编辑 数据传输过程中的封装示意图 无客户端认证的过程 有客户端认证的过程 SSL VPN的核心技术---虚拟网关技术 服务器验证的点: 资源…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...

python学习day39
图像数据与显存 知识点回顾 1.图像数据的格式:灰度和彩色数据 2.模型的定义 3.显存占用的4种地方 a.模型参数梯度参数 b.优化器参数 c.数据批量所占显存 d.神经元输出中间状态 4.batchisize和训练的关系 import torch import torchvision import torch.nn as nn imp…...
