为什么要用scrapy爬虫库?而不是纯python进行爬虫?
为什么要用scrapy爬虫库?而不是纯python进行爬虫?
- Scrapy的优点
- Scrapy节省的工作
- 使用纯Python编写爬虫的不足
Scrapy是一个使用Python编写的开源和协作的web爬虫框架,它被设计用于爬取网页数据并从中提取结构化数据。Scrapy的强大之处在于其广泛的功能和灵活性,可以让开发者高效地构建复杂的爬虫。下面是Scrapy的一些优点,以及它帮我们节省的工作和使用纯Python编写爬虫的潜在不足之处。
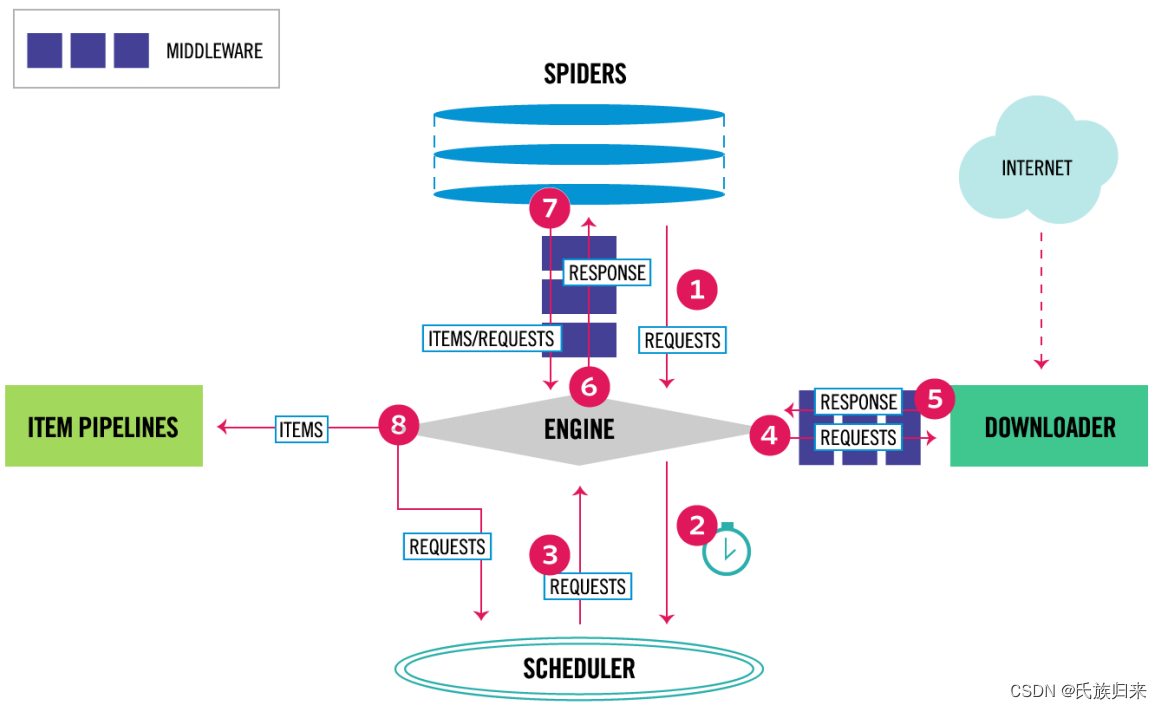
Scrapy的优点
- 内置的项目结构:Scrapy提供了一个清晰、易于管理的项目结构,这让开发、测试和部署爬虫变得更加简单和高效。
- 强大的选择器:它内置了对XPath和CSS选择器的支持,让提取数据变得非常简单和直观。
- 中间件和插件系统:Scrapy有一个灵活的中间件和插件系统,允许开发者自定义和扩展框架的功能,例如处理请求、响应、项目管道等。
- 内置的并发处理:Scrapy使用Twisted异步网络框架来处理网络通信,能够实现高效的并发请求,显著提高爬虫的抓取效率。
- 强大的抓取控制:提供了强大的抓取控制功能,包括自动重试、数据下载延迟、遵守robots.txt协议等。
- 易于扩展:可以轻松添加新的功能,如扩展项、管道和中间件。
- 数据导出:Scrapy可以轻松将抓取的数据导出到多种格式,如CSV、JSON、XML等。
Scrapy节省的工作
- 自动化请求调度和处理:Scrapy自动处理请求的发送、接收以及回调函数的调用,无需手动管理网络连接和数据流。
- 错误处理和重试机制:自动处理网络请求的错误,并且可以配置重试机制,降低临时网络问题对爬虫的影响。
- 遵循robots.txt策略:Scrapy可以配置为自动识别并遵守目标网站的robots.txt文件,减少手动检查的需要。
- 数据提取和处理的便利性:提供了强大的工具来提取和处理数据,减少了编写解析代码的复杂度。
- 高级功能的实现:如Cookies和Session的管理、用户代理的设置等,这在使用纯Python实现时可能需要大量的工作。
使用纯Python编写爬虫的不足
- 开发效率:不使用Scrapy等框架,开发同等功能的爬虫通常需要更多的时间和代码。
- 错误处理和稳定性:需要手动实现错误处理和重试逻辑,这可能导致代码更加复杂和难以维护。
- 并发处理:实现高效的并发或异步请求处理可能相对困难,需要对异步编程有深入的理解。
- 功能丰富性:自己编写可能难以快速实现Scrapy提供的一些高级功能,如中间件、信号等。
总的来说,Scrapy提供了一个高效、灵活且功能丰富的环境,大大减少了开发高性能爬虫所需的工作量。虽然使用纯Python也能实现相同的功能,但往往需要更多的时间和精力去处理底层的细节问题。
相关文章:

为什么要用scrapy爬虫库?而不是纯python进行爬虫?
为什么要用scrapy爬虫库?而不是纯python进行爬虫? Scrapy的优点Scrapy节省的工作使用纯Python编写爬虫的不足 Scrapy是一个使用Python编写的开源和协作的web爬虫框架,它被设计用于爬取网页数据并从中提取结构化数据。Scrapy的强大之处在于其广…...

C:数据结构王道
初始化顺序表(顺序表中元素为整型),里边的元素是1,2,3,然后通过scanf读取一个元素(假如插入的是6),插入到第2个位置,打印输出顺序表,每个元素占3个空格,格式为…...
Compose UI 之 Buttons 按钮 IconButtons 图标按钮
Buttons 按钮 Android Compose UI 库中的 Button 和 IconButton 是两种常用的组件,它们各自具有一些独特的特点。 Button 的特点: 可点击性:Button 是一个可点击的组件,通常用于触发某个操作或事件。文本内容:Button 通常包含文本内容,用于描述按钮的功能或操作。自定义…...
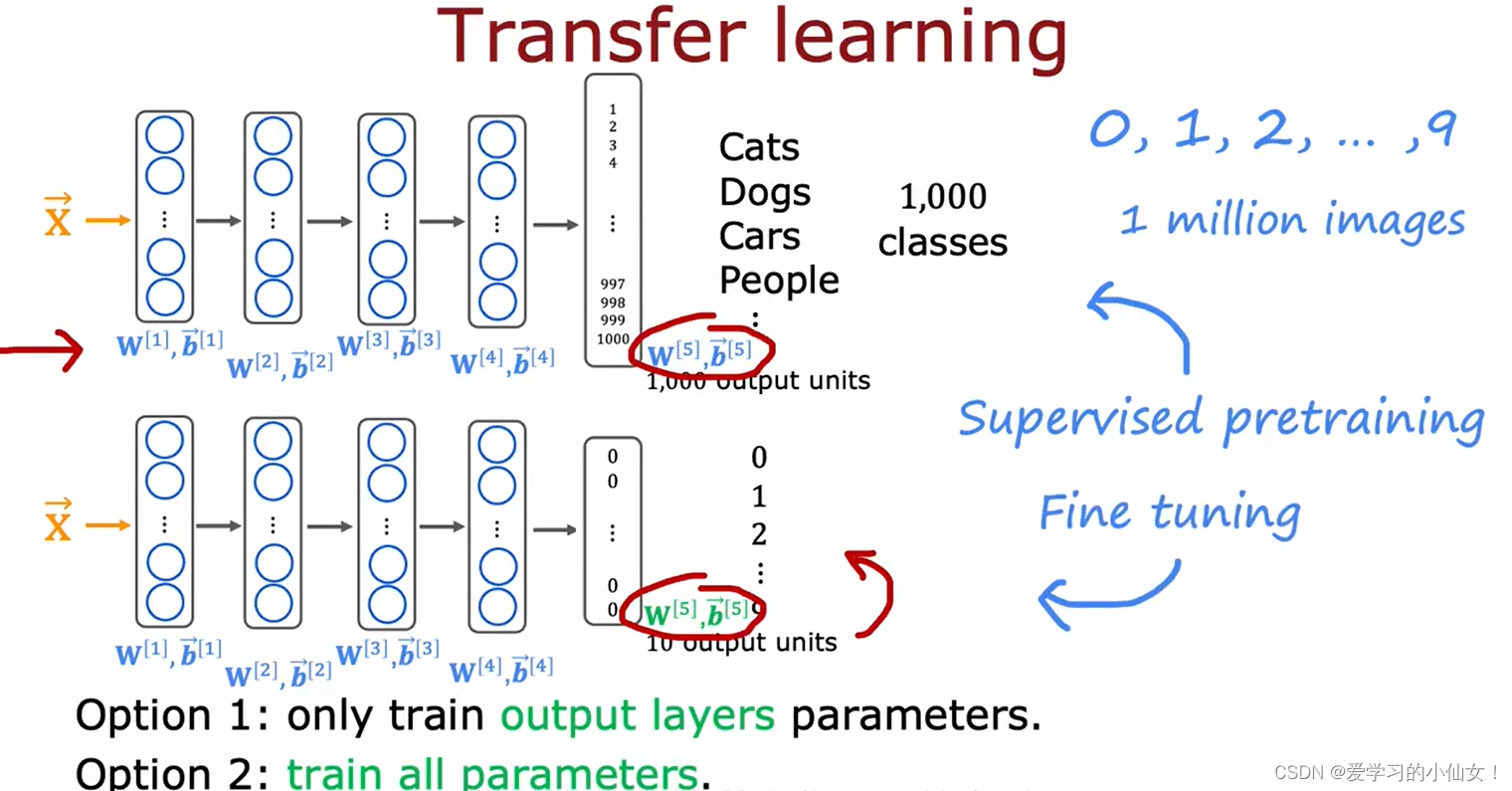
吴恩达机器学习笔记 二十一 迁移学习 预训练
迁移学习(transfer learning):直接把神经网络拿来,前面的参数可以直接用,把最后一层改了。 两种训练参数的方式: 1.只训练输出层的参数 2.训练所有参数 当只有一个小数据集的时候,第一种方法…...

Python中Pandas常用函数及案例详解
Pandas是一个强大的Python数据分析工具库,它为Python提供了快速、灵活且表达能力强的数据结构,旨在使“关系”或“标签”数据的操作既简单又直观。Pandas的核心数据结构是DataFrame,它是一个二维标签化数据结构,可以看作是一个表格…...
VR全景看房:超越传统的看房方式
近年来,新兴技术不断涌出,例如大数据、VR全景、人工智能、元宇宙等。随着科技不断发展,VR全景技术在房地产行业中的应用也是越发广泛,逐渐超越了传统的看房方式。今天,就让我们一起来深入探讨一下VR全景技术在VR看房中…...

pip 配置镜像加速安装
在使用pip安装Python第三方库时,默认是使用pip官网的非常慢,可通过配置国内镜像源加速下载速度,以下是如何使用国内镜像源安装Python库的两种常见方式: 临时使用镜像源安装 如果你只是想临时使用某个镜像源安装单个或几个库&…...

LUA语法复习总结
文章目录 简记变量数据类型运算符算术运算符关系运算符逻辑运算符杂项运算符 列表(表)表格操作表连接插入和删除排序表 模块元表__index 元方法实例 总结__newindex 元方法实例实例 为表添加操作符实例 __call 元方法实例 __tostring 元方法实例 简记 lua下标从1开始迭代器pai…...

某赛通电子文档安全管理系统 DecryptApplication 任意文件读取漏洞(2024年3月发布)
漏洞简介 某赛通电子文档安全管理系统 DecryptApplication 接口处任意文件读取漏洞,未经身份验证的攻击者利用此漏洞获取系统内部敏感文件信息,导致系统处于极不安全的状态。 漏洞等级高危影响版本*漏洞类型任意文件读取影响范围>1W 产品简介 …...

Mac-自动操作 实现双击即可执行shell脚本
背景 在Mac上运行shell脚本,总是需要开启终端窗口执行,比较麻烦 方案 使用Mac上自带的“自动操作”程序,将shell脚本打包成可运行程序(.app后缀),实现双击打开即可执行shell脚本 实现细节 找到Mac上 应用程序中的 自动操作&am…...
)
人工智能入门之旅:从基础知识到实战应用(六)
一、人工智能学习之路总结 人工智能学习的关键点与挑战可以总结如下: 关键点: 理论基础: 理解机器学习、深度学习等人工智能的基本原理和算法是学习的基础,包括线性代数、概率统计、微积分等数学知识,以及神经网络、…...

Debezium日常分享系列之:Debezium2.5稳定版本之Mysql连接器的工作原理
Debezium日常分享系列之:Debezium2.5稳定版本之Mysql连接器的工作原理 一、Mysql连接器的工作原理1.支持的 MySQL 拓扑2.MariaDB 支持3.Schema history topic4.Schema change topic5.Snapshots1)使用全局读锁的初始快照2)Debezium MySQL 连接…...

Linux服务器,使用ssh登录时越来越慢,有时甚至出现超时的现象,解决方案
一台Linux服务器,使用ssh登录时越来越慢,有时甚至出现超时的现象。一直以为这不算问题,但是有时候登录时间长的让人无法接受,查了一下,这“ssh登录慢”还真的是个问题,解决方案如下: 客户端进行…...

GPT-SoVITS开源音色克隆框架的训练与调试
GPT-SoVITS开源框架的报错与调试 遇到的问题解决办法 GPT-SoVITS是一款创新的跨语言音色克隆工具,同时也是一个非常棒的少样本中文声音克隆项目。 它是是一个开源的TTS项目,只需要1分钟的音频文件就可以克隆声音,支持将汉语、英语、日语三种…...

C#十大排序总结
一、冒泡排序 传送门 一、C#冒泡排序算法-CSDN博客 未完待续。。。...
Vue首屏优化方案
在Vue项目中,引入到工程中的所有js、css文件,编译时都会被打包进vendor.js,浏览器在加载该文件之后才能开始显示首屏。若是引入的库众多,那么vendor.js文件体积将会相当的大,影响首屏的体验。可以看个例子:…...

SpringBoot使用log4j2将日志记录到文件及自定义数据库
目录 一、环境说明 二、进行配置 1、pom.xml 2、log4j2.xml 3、CustomDataSourceProperties 4、ConfigReader 5、ConnectionFactory 连接工厂类,用于管理数据库连接 三、进行简单测试配置 1、LogUtils 2、LoginUserInfoHelper 3、LoginLogUtils 4、…...
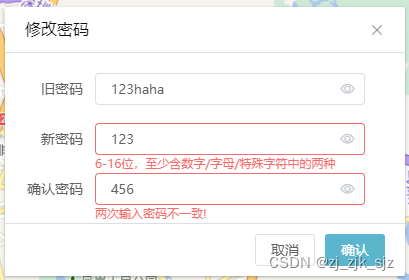
vue+elementUI用户修改密码的前端验证
用户登录后修改密码,密码需要一定的验证规则。旧密码后端验证是否正确;前端验证新密码的规范性,新密码规范为:6-16位,至少含数字/字母/特殊字符中的两种;确认密码只需要验证与新密码是否一致; 弹…...
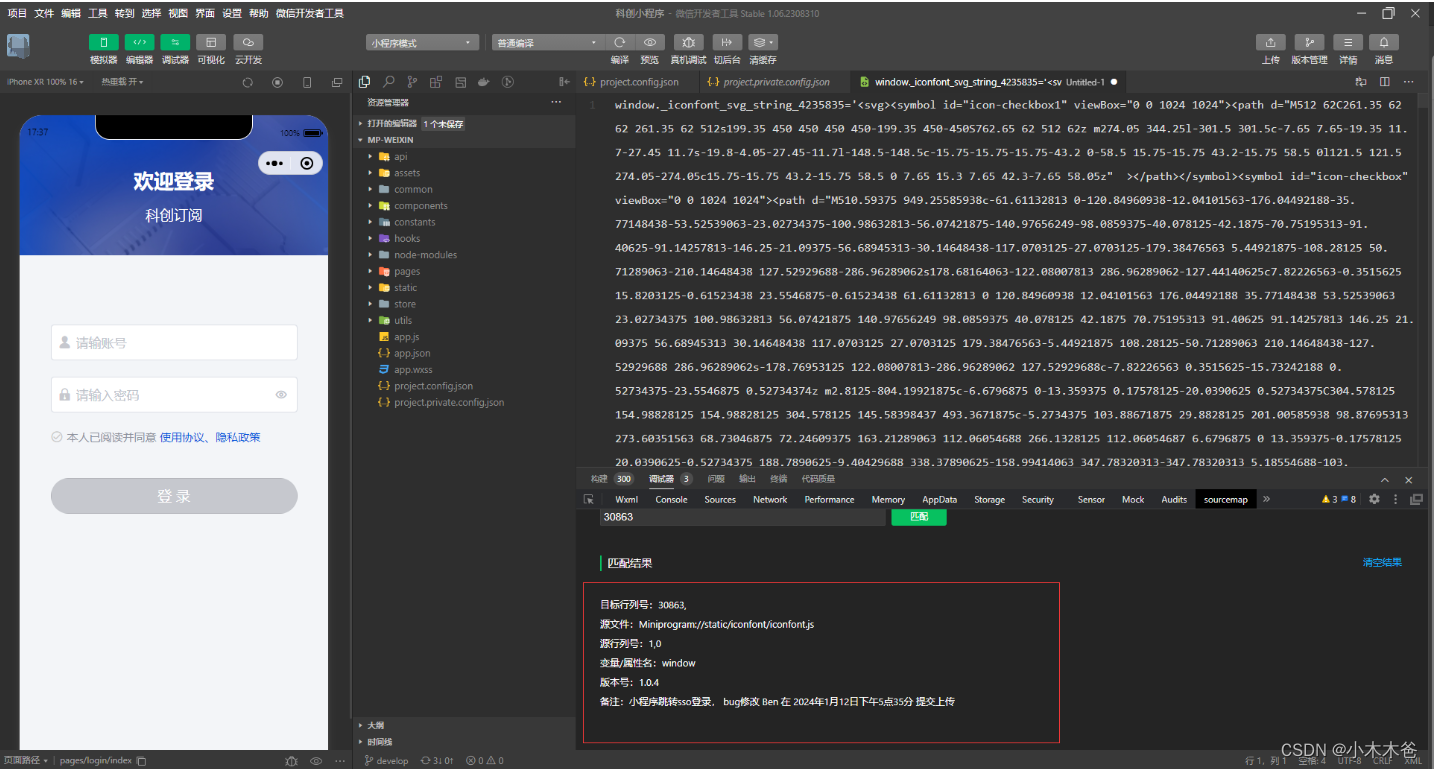
微信小程序问题定位——sourcemap文件
使用sourceMap在微信小程序中进行线上问题定位,主要可以通过以下步骤实现: 下载微信开发者工具首先,确保已经安装了微信开发者工具,这是进行小程序开发和调试的基础。登录微信公众平台并下载sourceMap文件:登录微信小…...

Photoshop_00000
简介 Adobe官网:https://www.adobe.com Adobe中文官网:https://www.adobe.com/cn Adobe中国服务商:http://adobe.sxbyu.cn/adobe/adobe_index?flag800&bd_vid5593893117402635109# Photoshop安装 基础操作 文件的打开和新建 打开文…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
)
window 显示驱动开发-如何查询视频处理功能(三)
D3DDDICAPS_GETPROCAMPRANGE请求类型 UMD 返回指向 DXVADDI_VALUERANGE 结构的指针,该结构包含特定视频流上特定 ProcAmp 控件属性允许的值范围。 Direct3D 运行时在D3DDDIARG_GETCAPS的 pInfo 成员指向的变量中为特定视频流的 ProcAmp 控件属性指定DXVADDI_QUER…...

联邦学习带宽资源分配
带宽资源分配是指在网络中如何合理分配有限的带宽资源,以满足各个通信任务和用户的需求,尤其是在多用户共享带宽的情况下,如何确保各个设备或用户的通信需求得到高效且公平的满足。带宽是网络中的一个重要资源,通常指的是单位时间…...
