java数据结构与算法刷题-----LeetCode47. 全排列 II
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 1. 暴力回溯
- 2. 分区法+回溯
此题为46题的衍生题,在46题的基础上,加上了是否重复的判断,除此之外完全一样。
| 🏆LeetCode46. 全排列https://blog.csdn.net/grd_java/article/details/136683863 |
|---|
1. 暴力回溯
| 解题思路:时间复杂度O( n n n^n nn),但是严格来说只到了O( n ∗ n ! n*n! n∗n!)。空间复杂度O(n) |
|---|
- 在46题的基础上增加一些判断是否重复的操作
- 首先我们先将数组排序,这样我们就能通过两个相邻值的比较,确定当前值是否是一个重复的值(不止一个它)
- 我们进行全排列时,每个位置可以选择任何不同的值,但是现在有重复的值,就必须确保同一个位置,重复的值只选一次
- 所以进行全排列时,通过比较相邻的值就可以判断了。但是必须是有序数组才行(重复数字会都挨在一起)
| 代码 |
|---|
int[] nums;boolean[] numsFlag;//flag数组,true表示当前这个值已经选过int len;List<List<Integer>> ans = new ArrayList<List<Integer>>();public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);this.nums = nums;this.len = nums.length;this.numsFlag = new boolean[len];ArrayList<Integer> records = new ArrayList<>();backTracking(records);return ans;}//回溯算法public void backTracking(List<Integer> records){if(records.size() == len) ans.add(new ArrayList<>(records));//全排列完成后,保存答案else{for(int i = 0;i<len;i++){//每个位置都可以选任何值,但是如果当前数字已被选过,则必须跳过这个值//如果当前值已被选,跳过! 或者 当前值和上一个一样 并且 上一个也没有被选(说明上一个就已经不能选,选了会重复了)if(this.numsFlag[i]==true || (i>0 && nums[i] == nums[i-1] && this.numsFlag[i-1] == false) ) continue;this.numsFlag[i] = true;//标志为被选过records.add(nums[i]);//选择这个数字backTracking(records);//进行下一个数字的枚举this.numsFlag[i] = false;//枚举完成后,放弃这个值records.remove(records.size()-1);//尝试当前位置下一个可能的值}}}
2. 分区法+回溯
| 解题思路:时间复杂度O( n ∗ n ! ∗ l o g 2 n n*n!*log_2{n} n∗n!∗log2n),其中 l o g 2 n log_2{n} log2n是判断是否重复的时间开销。空间复杂度O(n) |
|---|
- 含有重复的元素序列,进行全排列,这个方法就不太好用,因为处理重复很麻烦
- 所以这里只能通过笨办法,每次选择数字判断是否重复时,从当前位置可选值中,依次遍历判断我们当前要选的数字是否之前就存在过
- 这个算法依然不需要flag数组标志数字是否已经选择过,也不需要事先排序。
- 与46题代码几乎完全照搬,只单纯加了一个循环遍历数组,判断是否重复的方法而已。
| 代码 |
|---|
class Solution {int[] nums;int len;List<List<Integer>> ans = new ArrayList<List<Integer>>();public List<List<Integer>> permuteUnique(int[] nums) {this.nums = nums;this.len = nums.length;dfs(0);return ans;}private void dfs(int idx) {if (idx == len) {List<Integer> result = new ArrayList<>();for (int num: nums) result.add(num);ans.add(result);}for (int i = idx; i < len; i++) {if (isRepeat(nums, idx, i)) continue;//与46题唯一的不同swap(nums, idx, i);dfs( idx + 1);swap(nums, idx, i);}}//log_2{n},判断当前位置i的取值,是否是重复的(之前取过的值)//与46题唯一的不同private boolean isRepeat(int[] nums, int idx, int i) {while (idx < i) if (nums[idx++] == nums[i]) return true;return false;}private void swap(int[] nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}
相关文章:
java数据结构与算法刷题-----LeetCode47. 全排列 II
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 1. 暴力回溯2. 分区法回溯 此题为46题的衍生题,在46题…...

✅技术社区—MySQL和ES的数据同步策略
使用Canal框架实现MySQL与Elasticsearch(ES)的数据同步确实可以提高实时搜索的准确性和效率。Canal通过模拟MySQL的binlog日志订阅和解析,实现了数据的实时同步。在这样的同步机制下,ES中的数据可以非常接近于MySQL数据库中的实时…...

LinearLayout和RelativeLayout对比
LinearLayout和RelativeLayout是Android中应用最为广泛的两种布局, 绝大部分UI均可以通过两种布局中的任何一种进行实现,其对比如下: LinearLayout: 1. LinearLayout可以实现子View按照权重分配显示区域,RelativeLayou…...
蓝桥杯深度优先搜索|剪枝|N皇后问题|路径之谜(C++)
搜索:暴力法算法思想的具体实现 搜索:通用的方法,一个问题如果比较难,那么先尝试一下搜索,或许能启发出更好的算法 技巧:竞赛时遇到不会的难题,用搜索提交一下,说不定部分判题数据很…...

大门对楼梯,怎么办?
中国是一个非常重视风水的国家,风水学发扬和流传已有几千年的历史,很多懂风水的人都知道,大门风水是其中非常重要的一环,因为大门风水直接影响全家人的各种运势。大门风水好,能帮助你一臂之力;若大门风…...

解决驱动开发中<stdlib.h> no such file 的问题
前言 在进行驱动开发时,需要使用malloc等函数,导入C库<stdlib.h>出现bug。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏,一起讨论…...

Find My工牌|苹果Find My技术与工牌结合,智能防丢,全球定位
工作牌一般是由公司发行的,带有相关工作号及佩戴人信息的卡牌,一般由塑料制作而成。具有醒目.增强内部员工归属感等作用。主要构成为公司名字背景图片员工名字照片。胸牌是一种悬挂或串扣于上衣左方的一种工号牌或介绍小标牌,大多数佩戴在西装…...

Springboot解决跨域问题
跨域问题 在Spring Boot中解决跨域问题的原因是因为浏览器的同源策略(Same-Origin Policy)限制了从一个源加载的文档或脚本如何与来自另一个源的资源进行交互。如果前端页面和后端服务不在同一个源(域名、协议、端口号都不相同)&…...

UE5 C++ TPS开发 学习记录(10
p22 这节课把创建,查找,加入游戏房间的菜单类,以及插件内的系统类给补完了.说实话这节课有点绕,因为需要一直使用委托进行传值,先由菜单类Menu向系统类Subsystem发送函数传值请求,然后监听Subsystem的委托回调,同时系统类Subsystem向Session的工具发送请求,监听回调,再返回给M…...

ES6(一):let和const、模板字符串、函数默认值、剩余参数、扩展运算符、箭头函数
一、let和const声明变量 1.let没有变量提升,把let放下面打印不出来,放上面可以 <script>console.log(a);let a1;</script> 2.let是一个块级作用域,花括号里面声明的变量外面找不到 <script>console.log(b);if(true){let b1;}//und…...

Docker使用及部署流程
文章目录 1. 准备Docker环境2. 准备应用的Docker镜像3. 在服务器上运行Docker容器方法一:Docker Hub方法二:从构建环境传输镜像4. 管理和维护使用Docker Compose(可选)主要区别步骤 1: 安装Docker ComposeLinuxWindowMac步骤 2: 创建docker-compose.yml文件步骤 3: 使用Doc…...
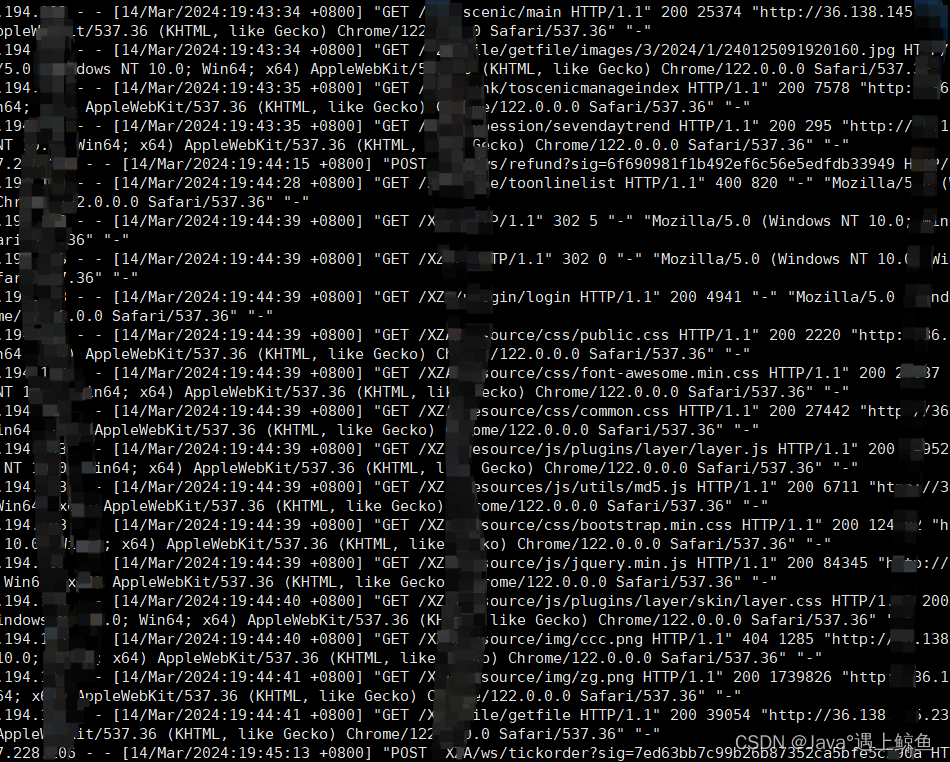
Nginx的日志怎么看,在哪看,access.log日志内容详解
Nginx 的日志文件通常位于服务器的文件系统中,具体位置可能因配置而异。以下是查看 Nginx 日志的几种方法: 1、查看访问日志:在默认配置下,Nginx 的访问日志文件路径为 /var/log/nginx/access.log。您可以通过命令 sudo cat /var…...
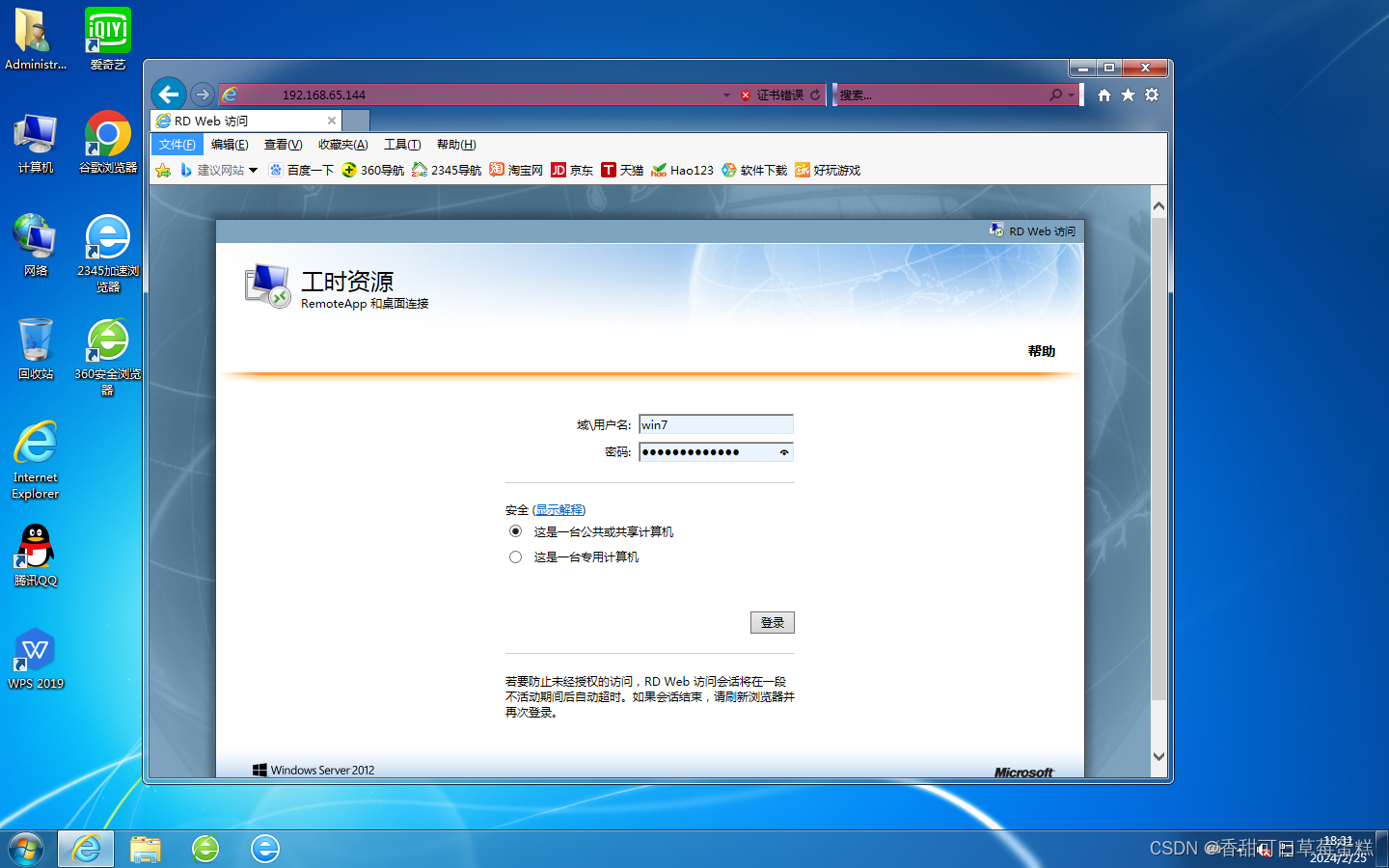
Windows Server 各版本搭建终端服务器实现远程访问(03~19)
一、Windows Server 2003 左下角开始➡管理工具➡管理您的服务器,点击添加或删除角色 点击下一步 勾选自定义,点击下一步 点击终端服务器,点击下一步 点击确定 重新登录后点击确定 点击开始➡管理工具➡计算机管理,展开本地用户…...
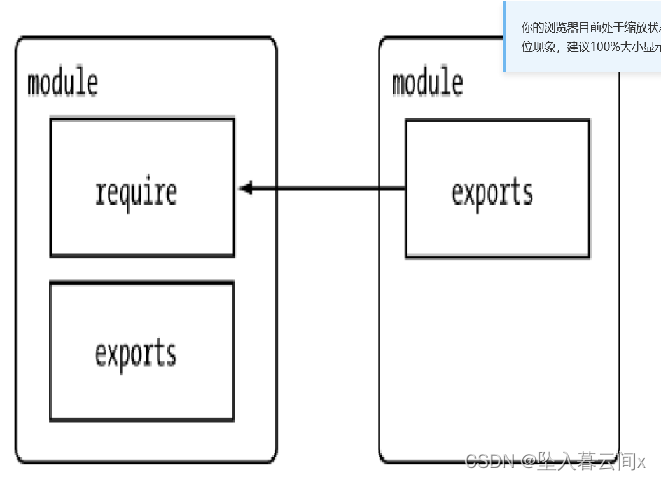
Node.js入门基础—day01
个人名片: 😊作者简介:一名大二在校生 🤡 个人主页:坠入暮云间x 🐼座右铭:给自己一个梦想,给世界一个惊喜。 🎅**学习目标: 坚持每一次的学习打卡 文章目录 初识node.js什…...

基于FPGA的PSRAM接口设计与实现
该系列为神经网络硬件加速器应用中涉及的模块接口部分,随手记录,以免时间久了遗忘。 一 PSRAM与HyperRAM 1、概述 2、异同 接口协议不同,因此在IP设计时需要注意。 Hyperram(Winbond):HyperBus协议 PSRAM(AP公司):X…...

OpenCV 图像的几何变换
一、图像缩放 1.API cv2.resize(src, dsize, fx0,fy0,interpolation cv2.INTER_LINEAR) 参数: ①src :输入图像 ②dsize:绝对尺寸 ③fx,fy:相对尺寸 ④interpolation:插值方法 2.代码演示 import cv2 …...
鸿蒙 - 读取 rawfile 中的 json 文件
一、说明 在以下目录中存放了一份地区 json 文件。 我想要将其读出来,并且转为我的实体类。 二、技术实现 import common from ohos.app.ability.common import { CityEntity } from ./entity/CityEntity import util from ohos.util;/*** App 内置的地区数据* r…...

【Stable Diffusion】入门-02:AI绘画提示词+参数设置攻略
目录 1 提示词1.1 分类和书写方式1.1.1 内容型提示词1.1.2 标准化提示词1.1.3 通用模板 1.2 权重1.2.1 套括号1.2.2 数字权重1.2.3 进阶语法 1.3 负面提示词 2 参数详解2.1 Sampling steps2.2 Sampling method2.3 Width, Height2.4 CFG Scale2.5 Seed2.6 Batch count, Batch si…...

Spring Boot启动时执行初始化操作的几种方式
场景 项目中,经常需要在启动过程中初始化一些数据,如从数据库读取一些配置初始化,或从数据库读取一些热点数据到redis进行初始化缓存。 方式一:实现CommandLineRunner 接口重写run方法逻辑 CommandLineRunner是Spring提供的接口࿰…...
考研失败, 学点Java打小工——Day3
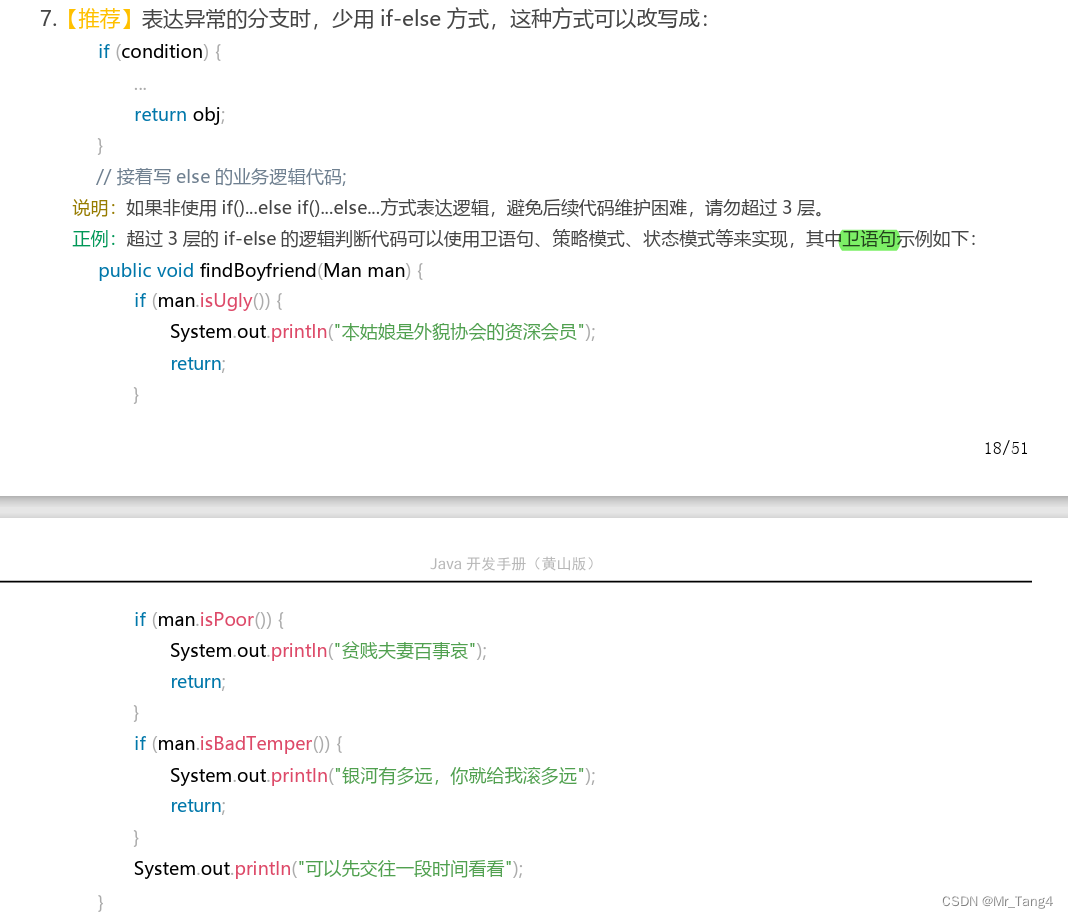
1 编码规范——卫语句 表达异常分支时,少用if-else方式。 比如成绩判断中对于非法输入的处理: /*>90 <100 优秀>80 <90 良好>70 <80 一般>60 <70 及格<60 不及格*/Testpu…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...