如何将办公资料文件生成二维码?扫码可看详情
日常办公的时候,经常会需要应用二维码来向同事或者客户发送和展示一些资料。比如包含企业介绍和产品介绍的资料、一些操作流程的资料、产品展示宣传视频、活动安排详情、比赛流程、会议资料… 这些都能通过一个文件二维码来展示。
文件二维码支持将PDF文件生成二维码,也支持将一个音频文件生成二维码,还可以将视频生成二维码,以及海报生成二维码…

一、文件二维码的优势
在二维彩虹,通过【文件】功能,就可以将文件资料生成二维码了。扫一扫二维码,便能立即阅读二维码里面的文件资料内容了。使用起来非常方便!
(1)随时阅读
和纸质的文件、电子版的文件不同,二维码可以被应用在线上线下多个场景中,不受空间、时间的限制,只要有手机,就能通过扫一扫即刻访问二维码背后的文件内容。你可以直接通过微信群将文件二维码分享给同时查阅,也可以将二维码打印在宣传手册上,供大家阅览。应用非常便利!
不论是图文内容,还是视频内容,都可以生成二维码。

(2)快速分享
有了文件二维码,也能轻松和位于不同城市、不同国家的同事、客户分享资料。而且在二维彩虹生成的文件二维码,会自带一个短链接。不论你扫描文件二维码,还是打开短链接,都可以访问页面的文件内容。所以,在电脑端浏览器访问文件二维码的短链接,也可以查看了。
(3)随时更新
因为这个文件二维码是一个动态二维码(活码),所以,在二维码生成后,已经发布使用的情况下,还可以随时在后台去更新二维码里面的文件。更新后,再扫描二维码,就能看到最新的内容了。
也就是说,在原二维码不变的情况下,可以随时更新二维码里面的内容。
(4)安全可加密
在二维彩虹,还可以为您制作的文件二维码设置一个查看密码,实现文件资料保密。只有知道密码的人,才能在扫码后查看到文件内容。
制作文件二维码
(5)追踪扫描数据
因为是一个活码,所以可以追踪文件二维码的扫描数据,比如扫描数量、扫描时间、扫描位置等数据。这些都可以在二维彩虹账号后台了解到。您只需要登录二维彩虹官网,从主页右上角【我的账号】-【数据概览】这个页面找到二维码,并查看数据即可。
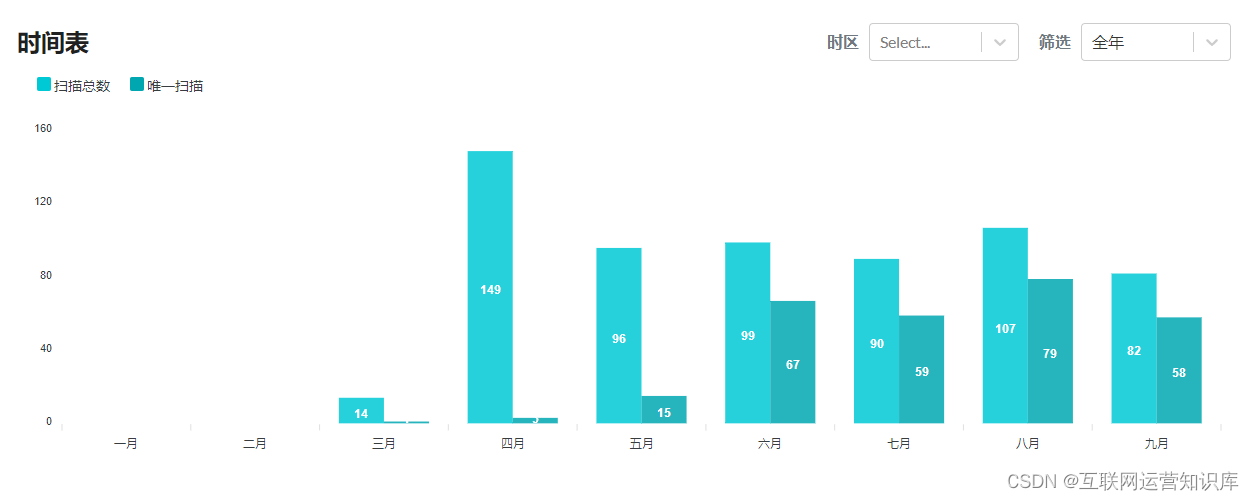
(6)应用范围广泛
其实,除了日常办公之外,文件二维码的应用范围也很广泛。比如在一些展览现场,用二维码来展示作品介绍;求职者将简历文件生成二维码;老师将学习资料生成二维码;商家在产品包装上展示产品说明书二维码…
二、如何将一个PDF文件生成二维码?
下面来和我们一起看看如何在二维彩虹生成PDF文件二维码吧。
第一步:登录二维彩虹二维码生成器官网
第二步:制作PDF文件二维码
选择【文件】选项,将准备好的PDF文件上传,然后点击生成二维码。不过这里需要注意,新用户使用需要先完成备案,且注意上传文件大小。
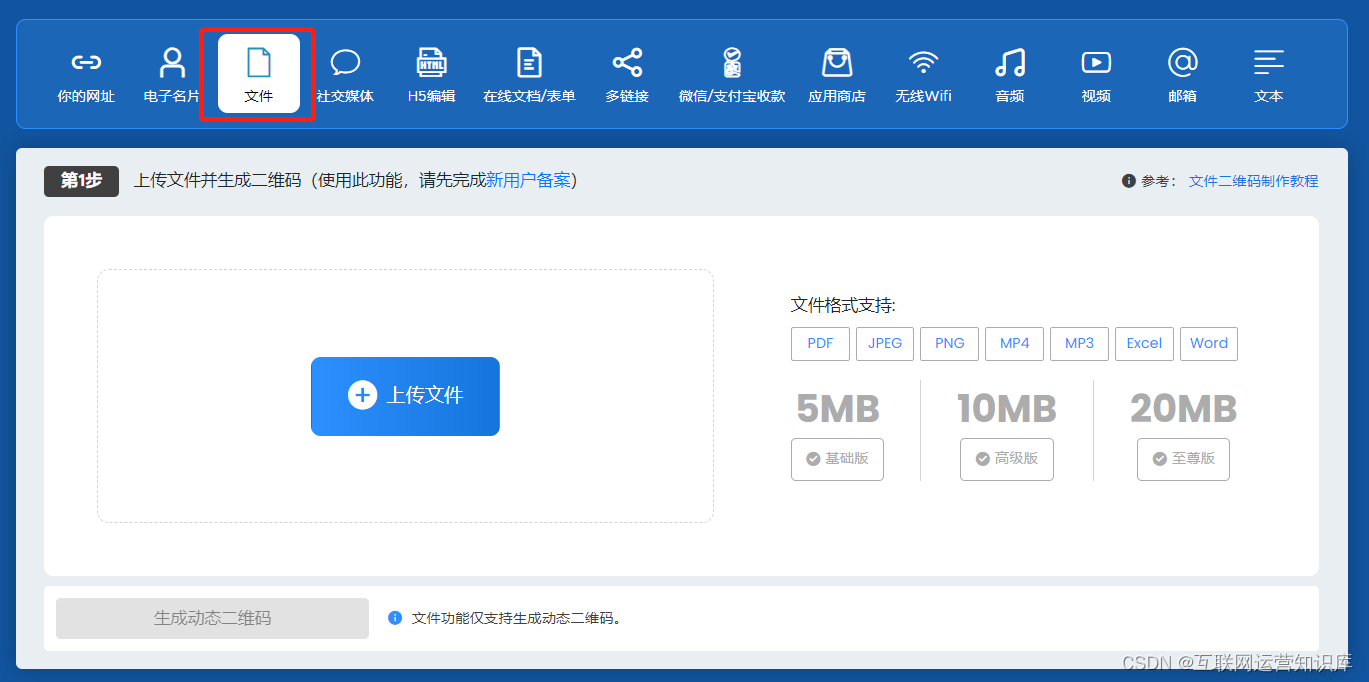
第三步:美化PDF文件二维码
根据使用需要,对二维码做一些美化和设计。二维码的颜色可以自己设计渐变彩色,且渐变方向可以自己调整。边框样式也有很多种选择,边框颜色自己设计,并且注意边框文字编辑,比如“立即扫描”、“会议资料”…之类的文字。还可以上传logo或相关图像展示在二维码图片中间。
第四步:测试文件二维码
在正式下载之前,请先对二维码做一个扫描测试。确保您的二维码可以被正常识别出来,并且展示的二维码内容都无误。最后,再点击下载二维码。
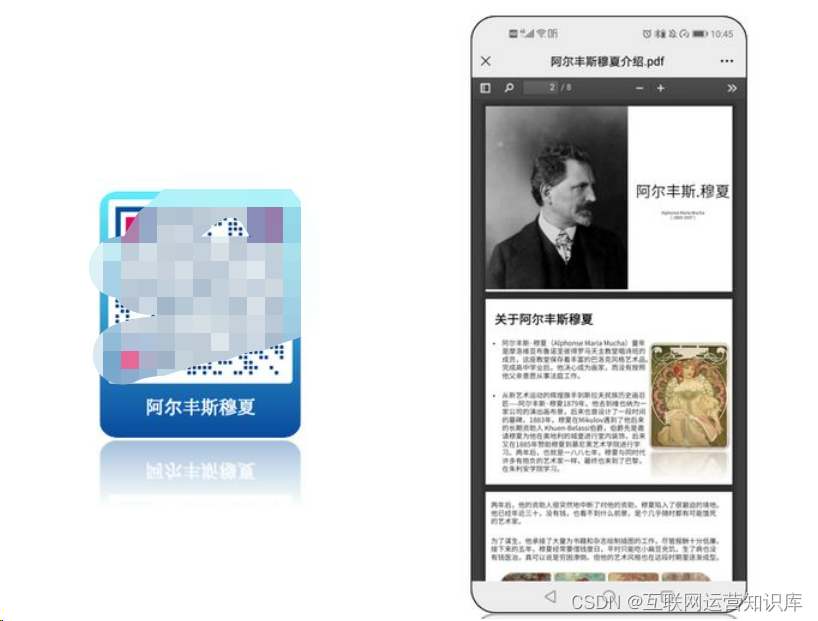
这样您的PDF文件就成功转成一个二维码了。扫码就就能查看内容。
三、怎样将多个文件生成一个二维码?
在二维彩虹,如果想要将多个文件展示在一个二维码中,或者希望将图文视频PDF等内容编辑在一个二维码中展示,那么可以通过二维彩虹的【H5编辑二维码】实现。
效果如下:

制作界面如下所示:
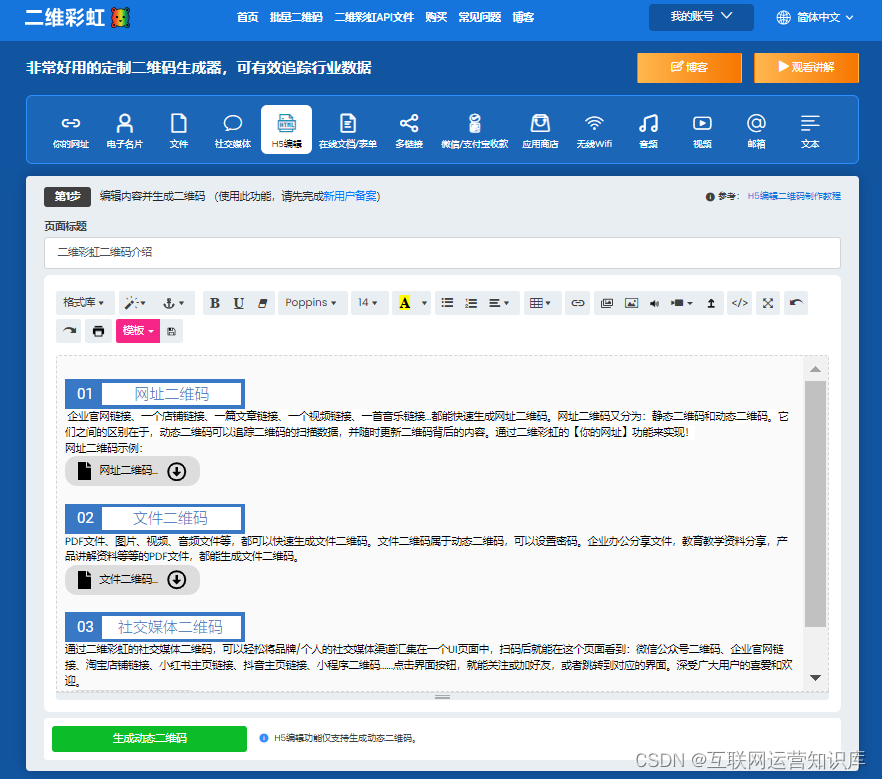
在H5编辑页面中,可以根据需要将多个文件上传,并编辑相关文字介绍,插入产品图片等。最后编辑排版完成,点击生成一个二维码!
以上就是今天关于文件生成二维码的全部内容了。
相关阅读:
音频故事二维码:如何制作一个扫码听故事的二维码?
这6款宝藏办公软件,真的好用到爆!
相关文章:

如何将办公资料文件生成二维码?扫码可看详情
日常办公的时候,经常会需要应用二维码来向同事或者客户发送和展示一些资料。比如包含企业介绍和产品介绍的资料、一些操作流程的资料、产品展示宣传视频、活动安排详情、比赛流程、会议资料… 这些都能通过一个文件二维码来展示。 文件二维码支持将PDF文件生成二维…...
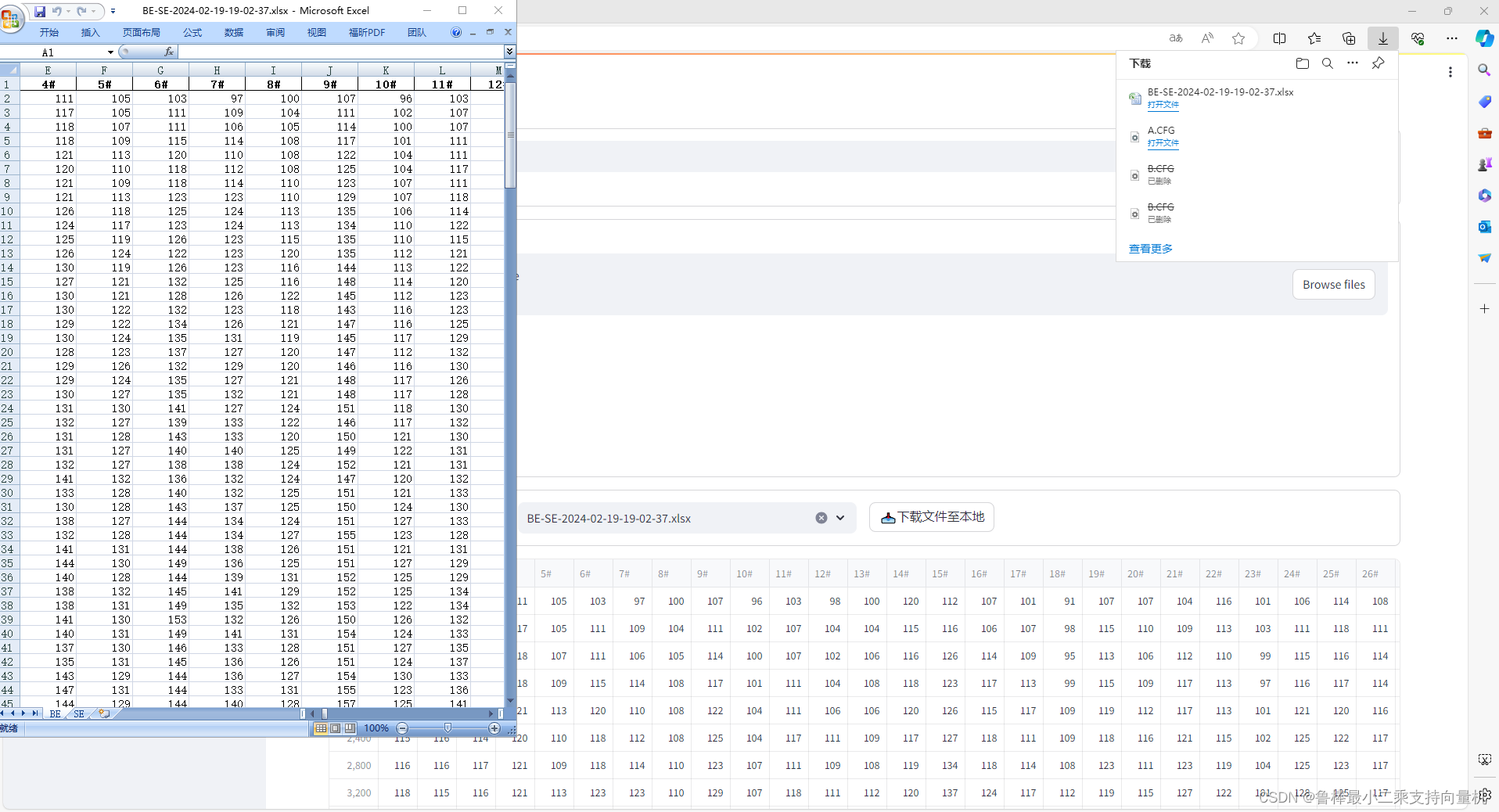
【Streamlit学习笔记】实现包含多个sheet的excel文件下载
1、什么是Streamlit Streamlit是一个免费的开源框架,用于快速构建和共享漂亮的机器学习和数据科学Web应用程序,官网链接 Streamlit Streamlit API链接 API reference 实际项目中遇到的问题:包含多个sheet的excel文件下载,下面将给…...

[Redis]——主从同步原理(全量同步、增量同步)
目录 Redis集群: 主从同步原理: replid和offset: 全量同步和增量同步: repl_baklog文件: 主从集群的优化: Redis集群: 部署多台Redis我们称之为Redis集群,他有一个主节点(负责写操作)&…...
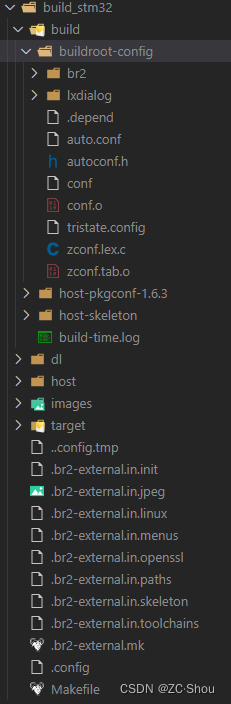
Buildroot 之二 详解构建架构、流程、external tree、示例
构建系统 Buildroot 中的构建系统使用的是从 Linux Kernel(4.17-rc2) 中移植的 Kconfig(配置) + Makefile & Kbuild(编译)这套构建系统,移植后的源码位于 support/kconfig/ 目录下。Buildroot 本身是一个构建系统,与直接编译源码不同,因此,它对这套系统进行了比较…...

牛客小白月赛61-C-小喵觅食
很经典的bfs,就是从猫咪和MM的坐标开始bfs搜索 不过这题有些小细节需要注意 1.认真审题,注意,猫一旦闻到小鱼干的味道,开始动,此时MM就不动了,一开始没仔细审题,很不好的习惯 2.注意移动的条件,vis,不是墙,距离是MM的移动距离范围内 3.这个猫咪的r2是闻味道的r2,不是移动距…...

200 名专家编写报告:AI 发展可能对人类构成「灭绝级威胁」
3 月 14 日消息,美国国务院委托编写了一份新报告,警告 AI 正呈指数级发展,可能会对人类构成「灭绝级威胁」。 这份报告全称为《提高先进人工智能安全保障的行动计划》,要求美国政府必须迅速、果断地采取行动,以避免 A…...

学习Android的第二十九天
目录 Android Service 与 Activity 通讯 范例 Android Service Alarm 定时广播 Alarm Alarm 使用流程 范例 Android IBinder Binder 为什么是 Binder ? Android Service 与 Activity 通讯 Activity 与 Service 通信的媒介就是 Service 中的 onBind() 方法࿰…...

SpringMVC重点记录
目录 1.学习重点2.回顾MVC3.回顾servlet4.初始SpringMVC4.1.为什么要学SpringMVC?4.2.SpringMVC的中重点DispatcherServlet4.3.SpringMVC项目的搭建4.4.MVC框架要做哪些事情?4.5.可能会遇到的问题 5.SpringMVC的执行原理6.使用注解开发SpringMVC7.Controller控制总结8.RestF…...

一条 SQL 更新语句如何执行的
Server 层 存储引擎层 总流程 查询语句 连接器 查询缓存 分析器 优化器 执行器 更新语句 redo log(节省的是随机写磁盘的 IO 消耗(转成顺序写&#x…...

Github上哪些好用的安全工具1
专注于web漏洞挖掘、内网渗透、免杀和代码审计,感谢各位师傅的关注!网安之路漫长,与君共勉! URLFinder 一款快速提取网页信息的工具。该项目可以快速爬取网页上的 URL 地址、JS 文件里的 API 接口等信息,支持批量抓取…...

手写Mybatis自动填充插件
目录 一、Mybatis插件简介🥙二、工程创建及前期准备工作🥫实现代码配置文件 三、插件核心代码实现🍗四、测试🥓 一、Mybatis插件简介🥙 Mybatis插件运行原理及自定义插件_简述mybatis的插件运行原理,以及如何编写一个…...
upload文件上传漏洞复现
什么是文件上传漏洞: 文件上传漏洞是指由于程序员在对用户文件上传部分的控制不足或者处理缺陷,而导致的用户可以越过其本身权限向服务器上上传可执行的动态脚本文件。这里上传的文件可以是木马,病毒,恶意脚本或者WebShell等。“…...
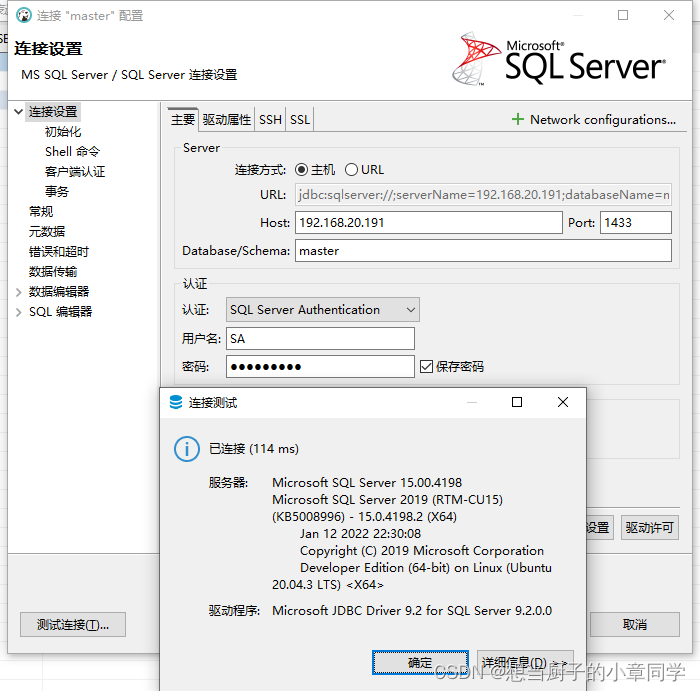
Docker 安装部署 SqlServer 数据库
Docker 安装部署 SqlServer 数据库 背景: 最近在开发数据中台数据集成模块,需要对接大量的数据做测试, 由于SqlServer 下载安装会耗费大量时间,所以采用 Docker 安装 Sqlserver 的方式部署数据库。 1、拉去 sqlserver 镜像 …...
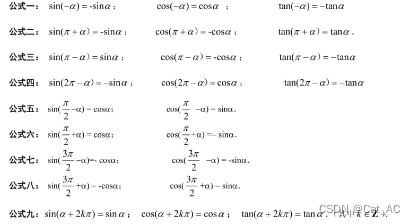
cmath 中cos sin等常用函数的坑(弧度角度换算)
cmath中三角函数的输入是弧度,不是角度.忘了这件事,找bug找了好久! 弧度是旧称弪。在数学和物理中,弧度是角的度量单位。它是由国际单位制导出的单位,单位缩写是rad。弧度是指在一个圆中,弧长和半径之比,即|弧度|弧长半径。 角度…...

深度解析HTTP反向代理-okey proxy
反向代理這個概念可能並不常見,但其實它對於提升網路安全和訪問速度方面發揮著很大作用。 HTTP反向代理(HTTP Reverse Proxy)是一種特殊的代理伺服器,首先它能夠接收互聯網上的連接請求,然後將這些請求轉發給內部網路…...

SwinIR训练报错解决
swinir训练报错解决 记录swinir图像超分重建算法复现过程中的报错信息,并提供相应的解决方案 报错信息 UserWarning: torch.meshgrid: in an upcoming release, it will be required to pass the indexing argument. (Triggered internally at C:\actions-runner\_work\pyto…...

C++类和对象一
#include <iostream> using namespace std;//设计一个学生类 class CStudent {public: //公有成员void InputData(){cout << "请输入学号";cin >> sno;cout << "请输入姓名";cin >> sname;cout << "请输入分…...

Linux之线程互斥
目录 一、问题引入 二、线程互斥 1、相关概念 2、加锁保护 1、静态分配 2、动态分配 3、锁的原理 4、死锁 三、可重入与线程安全 1、概念 2、常见的线程不安全的情况 3、常见的线程安全的情况 4、常见不可重入的情况 5、常见可重入的情况 6、可重入与线程安全联系…...
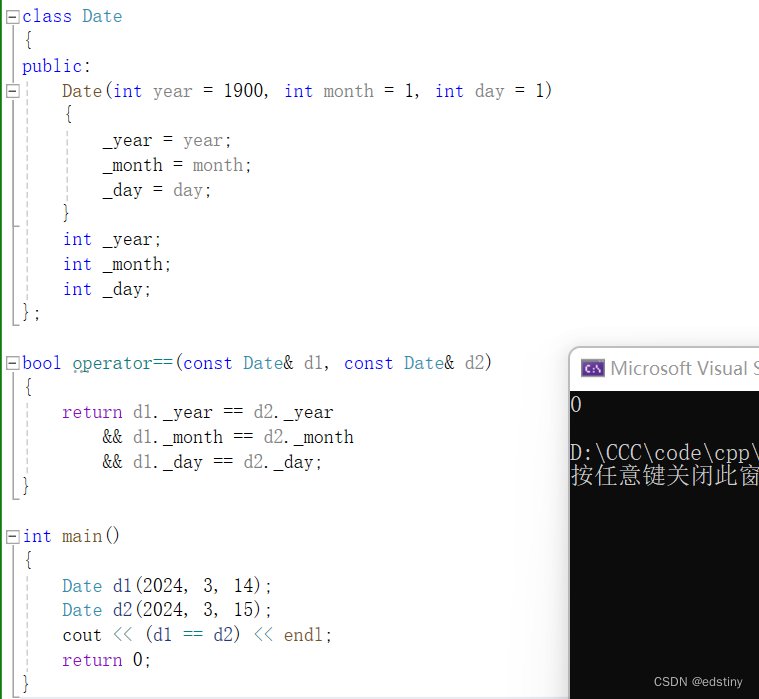
C++ 拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1. 引入 2. 拷贝构造的概念 3. 浅拷贝 4. 深拷贝 二. C运算符重载 1. 概念 2. 注意事项 3.举例 一. 拷贝构造函数 1. 引入 我们在创建对象时,能不能创建一个与原先对象一模一样的新对象呢?为了解决这个问题&#x…...

二刷代码随想录算法训练营第二十三天 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录 一、669. 修剪二叉搜索树 二、108. 将有序数组转换为二叉搜索树 三、538. 把二叉搜索树转换为累加树 一、669. 修剪二叉搜索树 题目链接:力扣 文章讲解:代码随想录 视频讲解: 你修剪的方式不对,我来给你纠正一下&#…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
