【分类讨论】【解析几何】【 数学】【推荐】1330. 翻转子数组得到最大的数组值
作者推荐
视频算法专题
本文涉及知识点
分类讨论 解析几何
LeetCode1330. 翻转子数组得到最大的数组值
给你一个整数数组 nums 。「数组值」定义为所有满足 0 <= i < nums.length-1 的 |nums[i]-nums[i+1]| 的和。
你可以选择给定数组的任意子数组,并将该子数组翻转。但你只能执行这个操作 一次 。
请你找到可行的最大 数组值 。
示例 1:
输入:nums = [2,3,1,5,4]
输出:10
解释:通过翻转子数组 [3,1,5] ,数组变成 [2,5,1,3,4] ,数组值为 10 。
示例 2:
输入:nums = [2,4,9,24,2,1,10]
输出:68
提示:
1 <= nums.length <= 3*104
-105 <= nums[i] <= 105
分类讨论
n = nums.length
一,不翻转。
二,翻转nums[0,i2)。i2 ∈ \in ∈ [0,n)。没必要翻转两个数组。
三,翻转nums[i1,n)。i1 ∈ \in ∈[0,n)。
四,翻转nums[i1,i2),i1不为0,i2不为n,i1和i2是合法下标,i1<i2。nums[i1-1]和nums[i2]都会发生变化。
翻转之前:|a-b|+|c-d| 翻转之后:|a-c|+|b-d|。
翻转后的数组值变大 ⟺ \iff ⟺ f(a,b,c,d) = |a-c|+|b-d| -|a-b|+|c-d| > 0。
令这4个数,下标从小大到大为a(nums[i1-1]),b(nums[i1]),c,d。
两点简化:
简化一,只需要考虑a <= c。
简化二,只需要考虑a <= b。
简化一证明
某组数a1,b1,c1,d1 ,a1 < c1 。
某外一组数{c1,d1,a1,b1} = f(c1,d1,a1,b1)=|c1-a1|+|d1-b1| - |c1-d1|-[a1-b1|
第一项第二项取反:|a1-c1|+|b1-d1|
第三项第四项互换:-|a1-b1|-|c1-d1|。
故:f(c1,d1,a1,b1) = f(a1,b1,c1,d1)
简化二证明:
某组数a1,b1,c1,d1 a1 > b1。
另外一组数{b1,a1,d1,c1} , f(b1,a1,d1,c1)=|b1-d1|+[a1-c1| -|b1-a1|-|d1-c1|
交换第一项和第二项目:|a1-c1|+|b1-d1|
第三项、第四项目,取反:-|a1-b1| - |c1,d1|
故:f(b1,a1,d1,c1) = f(a1,b1,c1,d1)。
等效问题
有一维四点a,b,c,d。 a <=b,a<=c。
线段ac的长度+线段bd的长度,能否大于线段ab的长度+线段cd的长度。
一,假定 b < c。

第一二种情况,两者有重合部分,长度不变。
第三四中情况,两者无重合部分,长度增加 两条线段的间隙 × \times × 2
二,b > c。

全部变短或不变,全部部分重合或全部重合。
结论
a<b a<c ,两条线段有重叠部分,则变短或不变。 没有重叠部分,变长间隙长度 × \times × 2。
上文已经证明了 两种简化的结果一样,现在来证明两个简化的判断条件一致。
简化一证明
某组数a1,b1,c1,d1 ,a1 < c1 。
简化前:线段a1b1和c1d1是否重叠。
简化后:线程c1d1和a1b1是否重叠。
两种显然等效。
简化二证明:
某组数a1,b1,c1,d1 a1 > b1。
线段a1b1就是b1a1,c1d1就是d1c1,所以无需证明。
重新简化
a<b 且b < c 且c<d。
ac的长度+bd的长度== ad的长度+bc的长度,都是ad的长度+bc的长度。
故调整a、b,使得a<b。调整c、d,使得c<d。
调整后增加的长度就是:(c-b)*2,结果为负数忽略。
代码
template<class ELE,class ELE2>
void MinSelf(ELE* seft, const ELE2& other)
{*seft = min(*seft,(ELE) other);
}template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}#define MacEnumMask(mask,maskMax) for (int mask = maskMax; mask; mask = (mask - 1) & maskMax) class Solution {
public:int maxValueAfterReverse(vector<int>& nums) {m_c = nums.size();long long ans = 0;for (int i = 0; i + 1 < m_c; i++){ans += abs(nums[i] - nums[i + 1]);}int iAdd = 0;for (int i = 1; i < m_c; i++){//交换nums[i,m_c)MaxSelf(&iAdd, abs(nums.back() - nums[i - 1]) - abs(nums[i] - nums[i - 1]));}for (int i = 1; i < m_c; i++){//交换nums[0,i)MaxSelf(&iAdd, abs(nums.front() - nums[i]) - abs(nums[i] - nums[i - 1]));}{//a,b在前 ,c,d在后int b = max(nums[0], nums[1]);for (int j = 2; j < m_c; j++){int c = min(nums[j - 1], nums[j]);int d = max(nums[j - 1], nums[j]);MaxSelf(&iAdd, 2 * c - 2 * b);MinSelf(&b, d);}}{//c,d在前 ,a,b在后int b = max(nums[m_c-1], nums[m_c-2]);for (int j = m_c-2; j >0 ; j--){int c = min(nums[j - 1], nums[j]);int d = max(nums[j - 1], nums[j]);MaxSelf(&iAdd, 2 * c - 2 * b);MinSelf(&b, d);}}return ans + iAdd;}int m_c;
};
测试用例
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{vector<int> nums;{Solution sln;nums = { 2,4,9,24,2,1,10 };auto res = sln.maxValueAfterReverse(nums);Assert(68, res);}{Solution sln;nums = { 2, 3, 1, 5, 4 };auto res = sln.maxValueAfterReverse(nums);Assert(10, res);}}
2023年5月
class Solution {
public:
int maxValueAfterReverse(vector& nums) {
m_c = nums.size();
int iTotal = 0;
for (int i = 0; i + 1 < m_c; i++)
{
iTotal += abs(nums[i] - nums[i + 1]);
}
//长度为1的子数组,结构不变。翻转整个数组结果不变
int iMaxAdd = 0;
//处理以索引0开头或m_c-1结尾的子数组
for (int i = 0; i + 1 < m_c; i++)
{
//翻转[0,i]
const int iLeft = abs(nums[i + 1] - nums[0]) - abs(nums[i + 1] - nums[i]);
//翻转[i+1,m_c)
const int iRight = abs(nums.back() - nums[i]) - abs(nums[i + 1] - nums[i]);
iMaxAdd = max(iMaxAdd, iLeft);
iMaxAdd = max(iMaxAdd, iRight);
}
int iMaxC = INT_MIN, iMinB = INT_MAX;
for (int i = 0; i + 1 < m_c; i++)
{
const int& x = nums[i];
const int& y = nums[i + 1];
iMaxC = max(iMaxC, min(x, y));
iMinB = min(iMinB, max(x, y));
}
iMaxAdd = max(iMaxAdd, 2 * (iMaxC - iMinB));
return iTotal + iMaxAdd;
}
int m_c;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【分类讨论】【解析几何】【 数学】【推荐】1330. 翻转子数组得到最大的数组值
作者推荐 视频算法专题 本文涉及知识点 分类讨论 解析几何 LeetCode1330. 翻转子数组得到最大的数组值 给你一个整数数组 nums 。「数组值」定义为所有满足 0 < i < nums.length-1 的 |nums[i]-nums[i1]| 的和。 你可以选择给定数组的任意子数组,并将该子…...

一文了解Spring的SPI机制
文章目录 一文了解Spring的SPI机制Java SPIServiceLoader Spring SPISpringboot利用Spring SPI开发starter 一文了解Spring的SPI机制 Java SPI SPI 全称 Service Provider Interface ,是 Java提供的一套用来被第三方实现或者扩展的接口,它可以用来启用…...
动态修改表名--方法一)
django根据时间(年月日)动态修改表名--方法一
方法一: 第一步:在models创建一个类,里边存放数据表中需要的字段,如下 class TemplateModel(models.Model):NowTime models.CharField(max_length5)name models.CharFiedld(max_length5)class Meta:abstract True # 基础类设…...
实现基本的登录功能
一、登录功能的前端处理过程 1、导入项目所需的图片和CSS等静态文件 参考代码存放client节点的/opt/code目录下 执行如下命令: [rootclient ~]# cp -r /opt/code/kongguan_web/src/assets/* /root/kongguan_web/src/assets/ 将参考代码中的css、icon、images等文…...

Java线程池实现原理及其在美团业务中的实践
随着计算机行业的飞速发展,摩尔定律逐渐失效,多核CPU成为主流。使用多线程并行计算逐渐成为开发人员提升服务器性能的基本武器。 J.U.C提供的线程池:ThreadPoolExecutor类,帮助开发人员管理线程并方便地执行并行任务。了解并合理…...

让AI给你写代码(四)—— 初步利用LangChain Agent根据输入生成,保存,执行
要进一步提升智能编码助手的效率,我觉得需要做到两点 1) 进一步让主人聚焦于设计输入以及结果验证的循环 2) 进一步让智能编码助手聚焦于代码实现和程序流程(保存、打开,修订、执行、合并…) 正好接触到LLM…...

Flutter does not exist
Flutter does not exist 原因:Generated.config 配置文件内路径缺失 原因:Flutter SDK缺失 通过配置文件查到Flutter SDK在本地的存放位置FLUTTER_FRAMEWORK_DIR/Users/haijunyan/Documents/flutter/bin/cache/artifacts/engine/ios 真机所需…...

AIX上安装gcc和g++
AIX的iso镜像中没有gcc的软件包,需要我们自己下载,我们可以在 Index of /download/rpmdb/deplists/aix72 下载对应gcc和g版本的依赖文件deps 我们使用的是4.9.4版本的软件包 我们首先安装gcc,在http://www.oss4aix.org/download/everythi…...
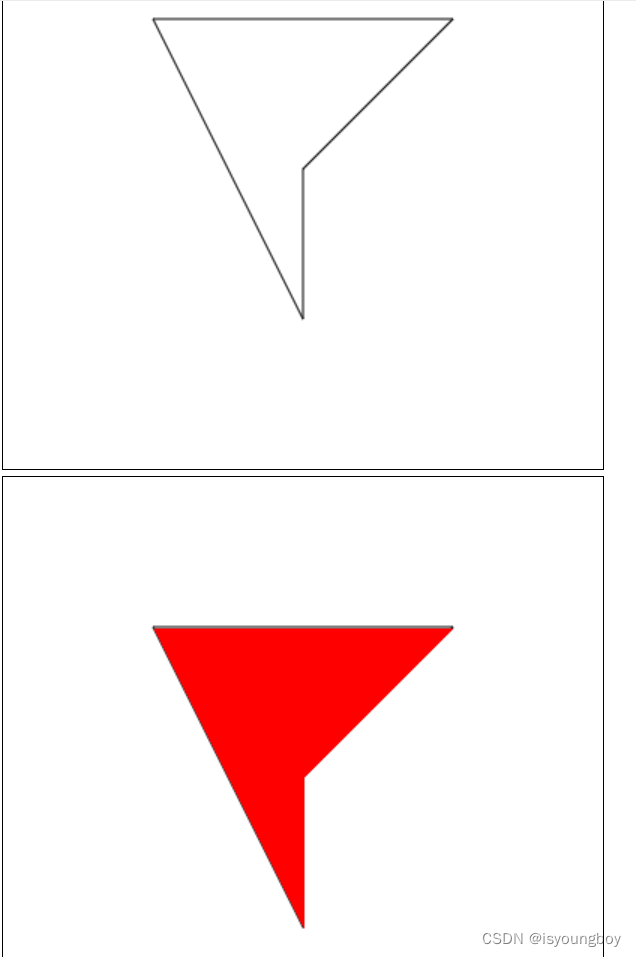
js实现扫描线填色算法使用canvas展示
算法原理 扫描线填色算法的基本思想是:用水平扫描线从上到下扫描由点线段构成的多段构成的多边形。每根扫描线与多边形各边产生一系列交点。将这些交点按照x坐标进行分类,将分类后的交点成对取出,作为两个端点,以所填的色彩画水平…...

考研模拟面试-题目【攻略】
考研模拟面试-题目【攻略】 前言版权推荐考研模拟面试-题目前面的问题通用问题专业题数据结构计算机网络操作系统数据库网络安全 手写题数据结构操作系统计算机网络 代码题基础代码题其他代码题 后面的问题补充题目 最后 前言 2023-10-19 12:00:57 以下内容源自《考研模拟面试…...

Frostmourne - Elasticsearch源日志告警配置
简介 配置Frostmourne 接入Elasticsearch源进行日志匹配告警,并静默规则,告警消息发送到企业微信,告警信息使用Markdown。 部署安装教程查看: https://songxwn.com/frostmourne_install ELK 安装教程:https://songx…...
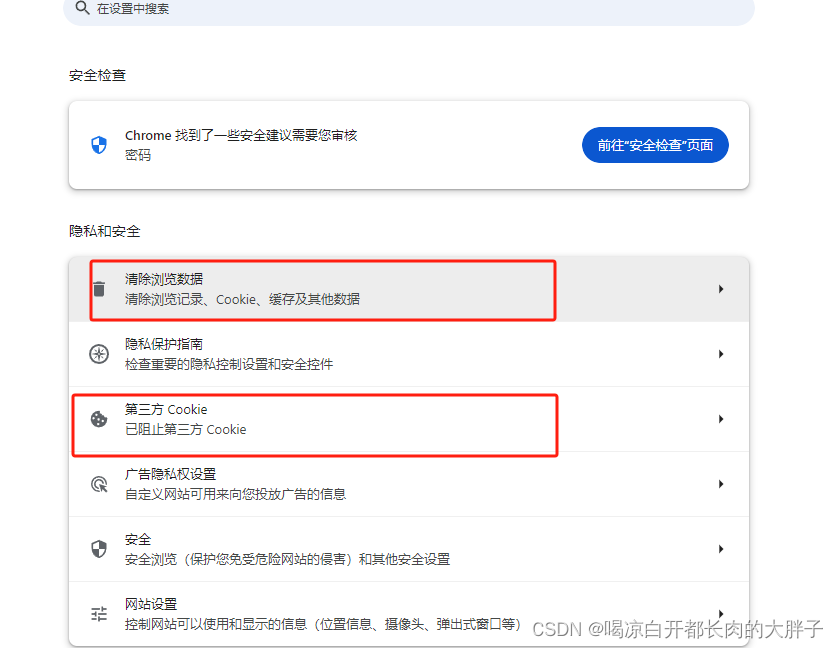
GPT出现Too many requests in 1 hour. Try again later.
换节点 这个就不用多说了,你都可以上GPT帐号了,哈…… 清除cooki 然后退出账号,重新登录即可...

python爬虫实战——小红书
目录 1、博主页面分析 2、在控制台预先获取所有作品页的URL 3、在 Python 中读入该文件并做准备工作 4、处理图文类型作品 5、处理视频类型作品 6、异常访问而被中断的现象 7、完整参考代码 任务:在 win 环境下,利用 Python、webdriver、JavaS…...
Linux信号机制
目录 一、信号的概念 二、定时器 1. alarm函数 2. setitimer函数 3.signal和sigaction函数 三、使用SIGCHLD信号实现回收子进程 一、信号的概念 概念:信号是在软件层次上对中断机制的一种模拟,是一种异步通信方式 。所有信号的产生及处理全部都是由内…...
区块链技术中的共识机制算法:以权益证明(PoS)为例
引言: 在区块链技术的演进过程中,共识机制算法扮演着至关重要的角色。除了广为人知的工作量证明(PoW)外,权益证明(Proof of Stake,PoS)也是近年来备受关注的一种共识算法。 …...

19113133262(微信同号)【征稿进行时|见刊、检索快速稳定】2024年区块链、物联网与复合材料与国际学术会议 (ICBITC 2024)
【征稿进行时|见刊、检索快速稳定】2024年区块链、物联网与复合材料与国际学术会议 (ICBITC 2024) 大会主题: (主题包括但不限于, 更多主题请咨询会务组苏老师) 区块链: 区块链技术和系统 分布式一致性算法和协议 块链性能 信息储存系统 区块链可扩展性 区块…...

Doris:使用表函数explode实现array字段列转行
文章目录 使用场景相关知识点介绍explodesplit_by_stringlateral view 具体实现和SQLlateral view explode列转行SPLIT_BY_STRING拆分字符串为数组element_at获取数据创建视图 使用场景 我们的大数据数据库,由clickhouse换成了doris我们有一张路口指标表࿰…...
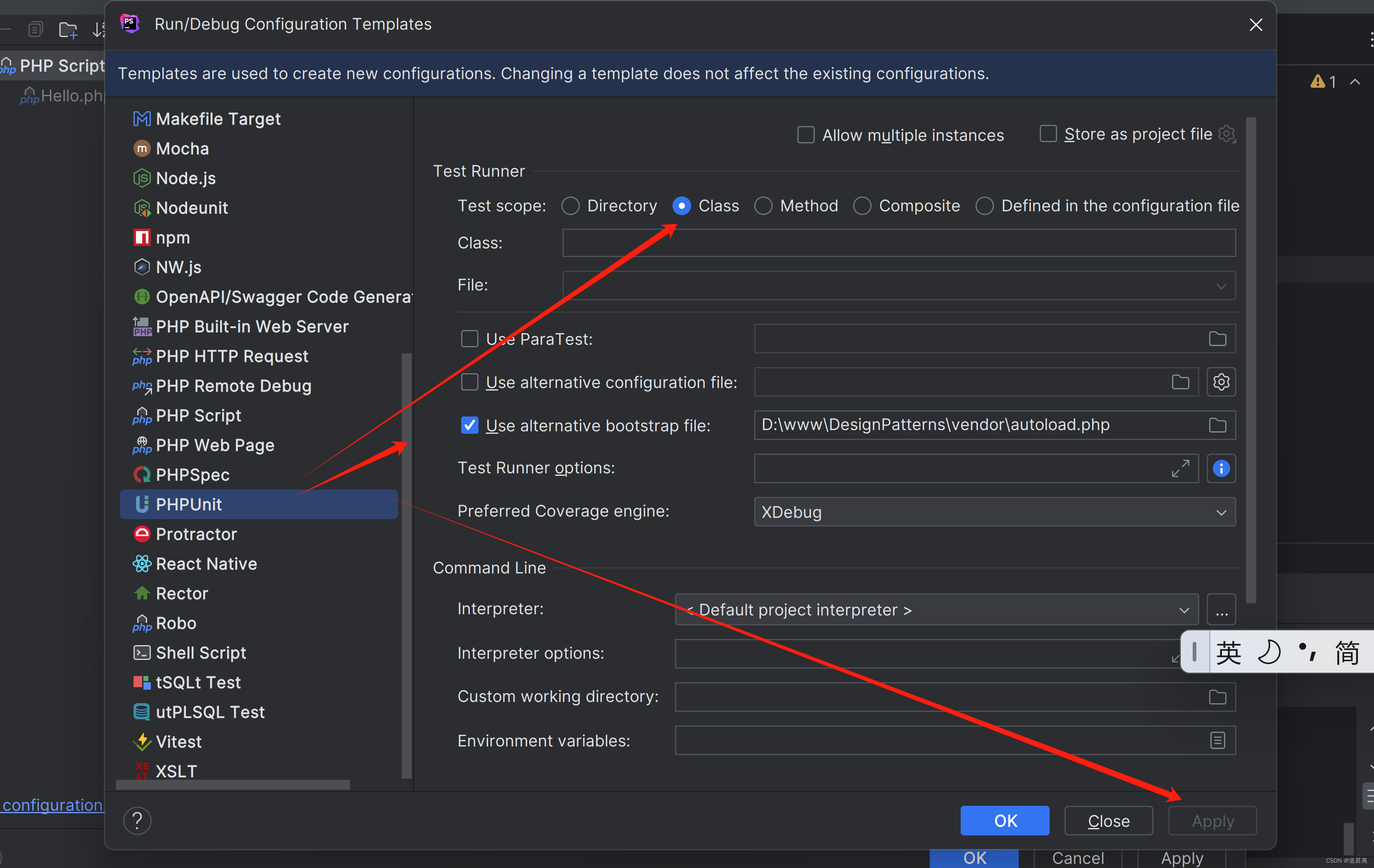
原生php单元测试示例
下载phpunit.phar https://phpunit.de/getting-started/phpunit-9.html 官网 然后win点击这里下载 新建目录 这里目录可以作为参考,然后放在根目录下 新建一个示例类 <?phpdeclare(strict_types1);namespace Hjj\DesignPatterns\Creational\Hello;class He…...
计算机毕业设计-springboot+vue前后端分离电竞社交平台管理系统部分成果分享
4.5系统结构设计 本系统使用的角色主要有系统管理员、顾客、接单员,本系统为后台管理系统,游客用户可以经过账号注册,管理员审核通过后,用账号密码登录系统,查看后台首页,模块管理(顾客信息&am…...

Stable Diffusion 详解
整体目标 文本生成图片;文本图片生成图片 网络结构 CLIP的文本编码器和图片生成器组成图像生成器,输入是噪声经过UNet得到图像特征,最后解码得到图像 前向扩散 模型直接预测图片难度比较大,所有让模型预测噪音然后输入-噪音…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
