WPF使用LiveCharts画图时,横坐标转换成时间
一、背景
使用LiveCharts画图时,横坐标通常为数值类型,要转换成时间等自定义类型,需要用到Formatter进行类型转换。
示例使用MVVM模式编写
二、View代码
关键是设置LabelFormatter属性
<lvc:CartesianChart Series="{Binding Series}"><lvc:CartesianChart.AxisX><lvc:Axis LabelFormatter="{Binding Formatter}"></lvc:Axis></lvc:CartesianChart.AxisX>
</lvc:CartesianChart>三、Model代码
public class DataPoint{public DateTime Date { get; set; }public double Value { get; set; }}四、ViewModel代码
4.1 设置数据映射
用Mappers将DateTime转换数值类型,这里使用了DateTime的Ticks进行转换
var dayConfig = Mappers.Xy<DataPoint>().X(dayModel => (double)dayModel.Date.Ticks / TimeSpan.FromHours(1).Ticks).Y(dayModel => dayModel.Value);4.2 设置数据映射转换格式
将转换后的数值类型还原成Datetime,再加上自定义的字符
Formatter = value => new DateTime((long)(value * TimeSpan.FromHours(1).Ticks)).ToString("t");4.3 后端代码
public ScatterChartViewModel(){// 初始化数据var dataPoints = new List<DataPoint>{new DataPoint { Date = new DateTime(2024, 3, 1), Value = 10 },new DataPoint { Date = new DateTime(2024, 3, 2), Value = 20 },new DataPoint { Date = new DateTime(2024, 3, 3), Value = 15 },// 添加更多数据点};var dayConfig = Mappers.Xy<DataPoint>().X(dayModel => (double)dayModel.Date.Ticks / TimeSpan.FromHours(1).Ticks).Y(dayModel => dayModel.Value);Series = new SeriesCollection(dayConfig){new ScatterSeries{Title = "Data Points",Values = new ChartValues<DataPoint>(dataPoints)}};Formatter = value => new DateTime((long)(value * TimeSpan.FromHours(1).Ticks)).ToString("t");}相关文章:

WPF使用LiveCharts画图时,横坐标转换成时间
一、背景 使用LiveCharts画图时,横坐标通常为数值类型,要转换成时间等自定义类型,需要用到Formatter进行类型转换。 示例使用MVVM模式编写 二、View代码 关键是设置LabelFormatter属性 <lvc:CartesianChart Series"{Binding Series…...
Qt客户端开发的技术难点
在Qt客户端开发中,可能会遇到一些技术难点,这些难点可能与UI设计、性能优化、跨平台兼容性等方面有关。以下是一些可能的技术难点,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作…...

杰理AD155儿童玩具语音集成电路
一、杰理AD155集成电路是由杰理科技设计、开发和销售的一款产品,AD15系列 SoC 芯片支持以下特性: 工作电压:2.0V-5.5V主频可达120MHz的32bitCPU,片上集成20K字节SRAM,8K字节ICache支持最多2路解码同时运行,支持F1A/A/…...
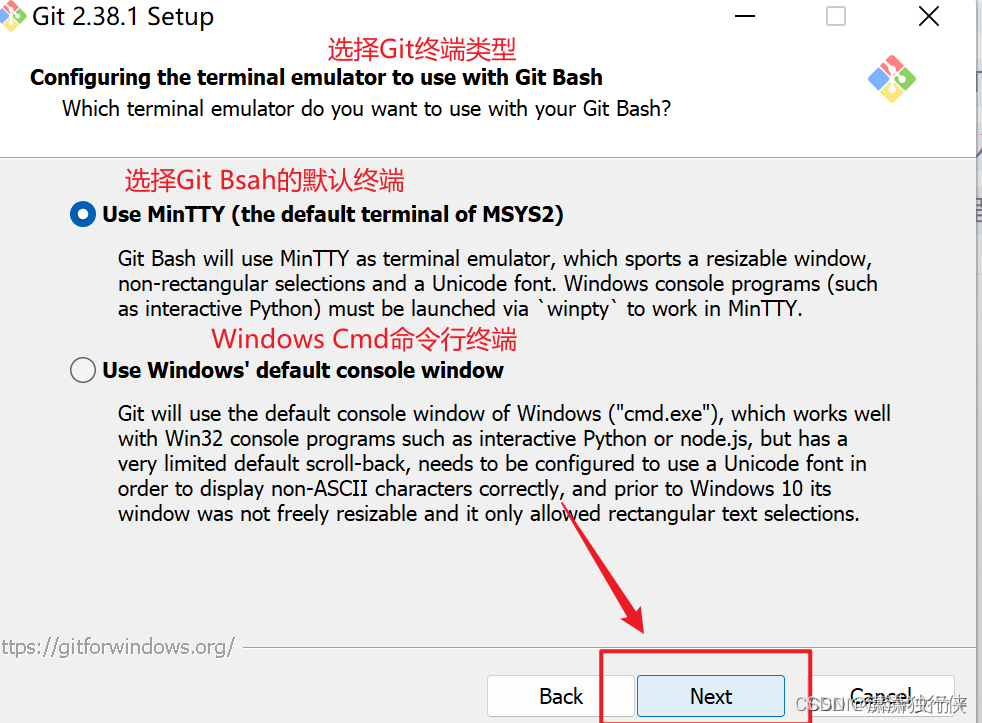
git bash 命令行反应慢、卡顿(定位出根本原因)
参考该博主: https://blog.csdn.net/weixin_50212044/article/details/131575987?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-131575987-blog-130024908.235v43pc_blog_bottom_relevance_base4&spm1001.210…...
)
Android 启动service(Kotlin)
一、使用startForegroundService()或startService()启用service **Activity //启动service val intent: Intent Intent(ServiceActivitythis,MyService::class.java) //Build.VERSION_CODES.O 26 // Android8以后,不允许后台启动Service i…...
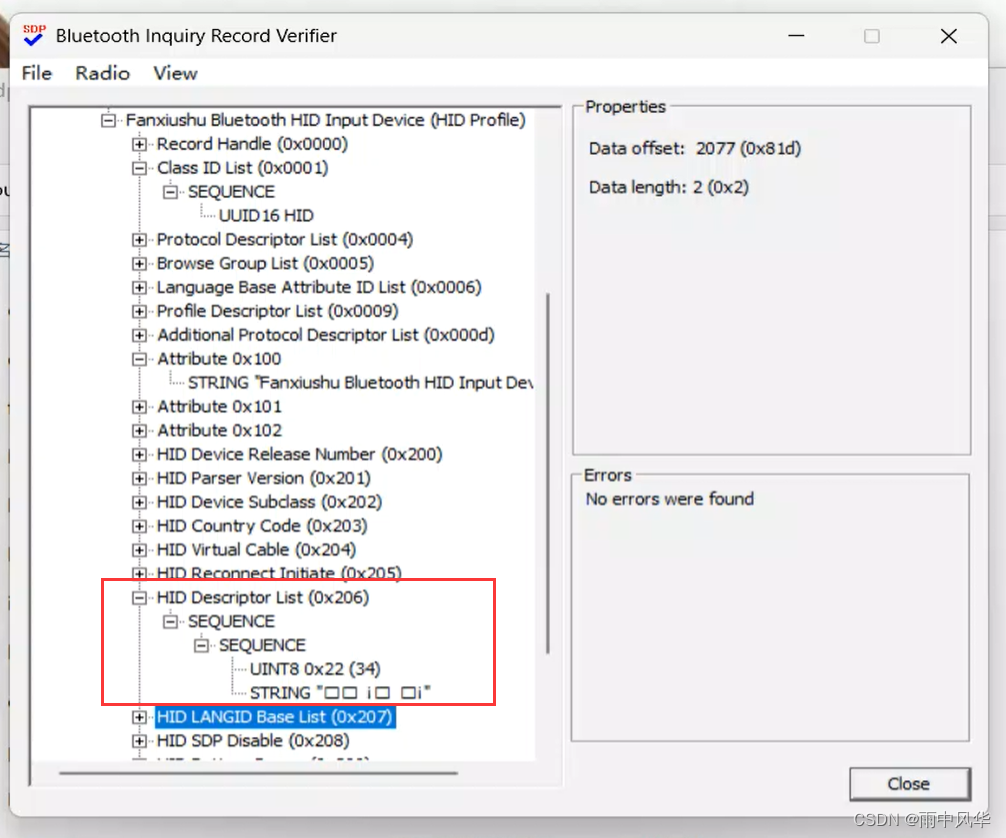
Windows蓝牙驱动开发之模拟HID设备(一)(把Windows电脑模拟成蓝牙鼠标和蓝牙键盘等设备)
by fanxiushu 2024-03-14 转载或引用请注明原作者 把Windows电脑模拟成蓝牙鼠标和蓝牙键盘,简单的说,就是把笨重的PC电脑当成鼠标键盘来使用。 这应该是一个挺小众的应用,但有时感觉也应该算比较好玩吧, 毕竟实现一种一般人都感觉…...

LlamaParse: 高效的PDF文件RAG解析工具
LlamaParse: 高效的PDF文件RAG解析工具 通过Thomas Reid的深入探索,LlamaParse成为了目前我所见最优秀的RAG实现用PDF解析器。基于AI的技术,尤其在处理像SEC Q10这样的复杂文件时表现出色,这些文件通常包含文本、数字及其组合构成的表格&…...

platform设备注册驱动模块的测试
一. 简介 上一篇文章编写了 platform设备注册代码,文章地址如下: 无设备树platform驱动实验:platform设备注册代码实现-CSDN博客 本文继续无设备树platform驱动实验,本文对编译好的 设备注册程序进行测试,测试所实…...

鸿蒙Harmony应用开发—ArkTS声明式开发(容器组件:ListItemGroup)
该组件用来展示列表item分组,宽度默认充满List组件,必须配合List组件来使用。 说明: 该组件从API Version 9开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。该组件的父组件只能是List。 使用说明 当List…...

Docker:常用命令
文章目录 docker作用常用指令 docker 作用 Docker 是一种容器化平台,可以让开发者打包应用程序及其依赖项,并以容器的形式进行发布、交付和运行。 Docker 的一些主要作用: 应用程序隔离:Docker 使用容器技术,将应用程…...

如何搭建“Docker Registry私有仓库,在CentOS7”?
1、下载镜像Docker Registry docker pull registry:2.7.1 2、运行私有库Registry docker run -d -p 5000:5000 -v ${PWD}/registry:/var/lib/registry --restartalways --name registry registry:2.7.1 3、拉取镜像 docker pull busybox 4、打标签,修改IP&#x…...

DBA面试题:MySQL缓存池LRU算法做了哪些改进?
下图是MySQL(MySQL5.7版本)体系架构图 MySQL的InnoDb Buffer Pool 缓冲池是主内存中的一个区域,用来缓存InnoDB在访问表和索引时的数据。对于频繁使用的数据可以直接从内存中访问,从而加快处理速度。如果一台服务器专用作MySQL数据…...
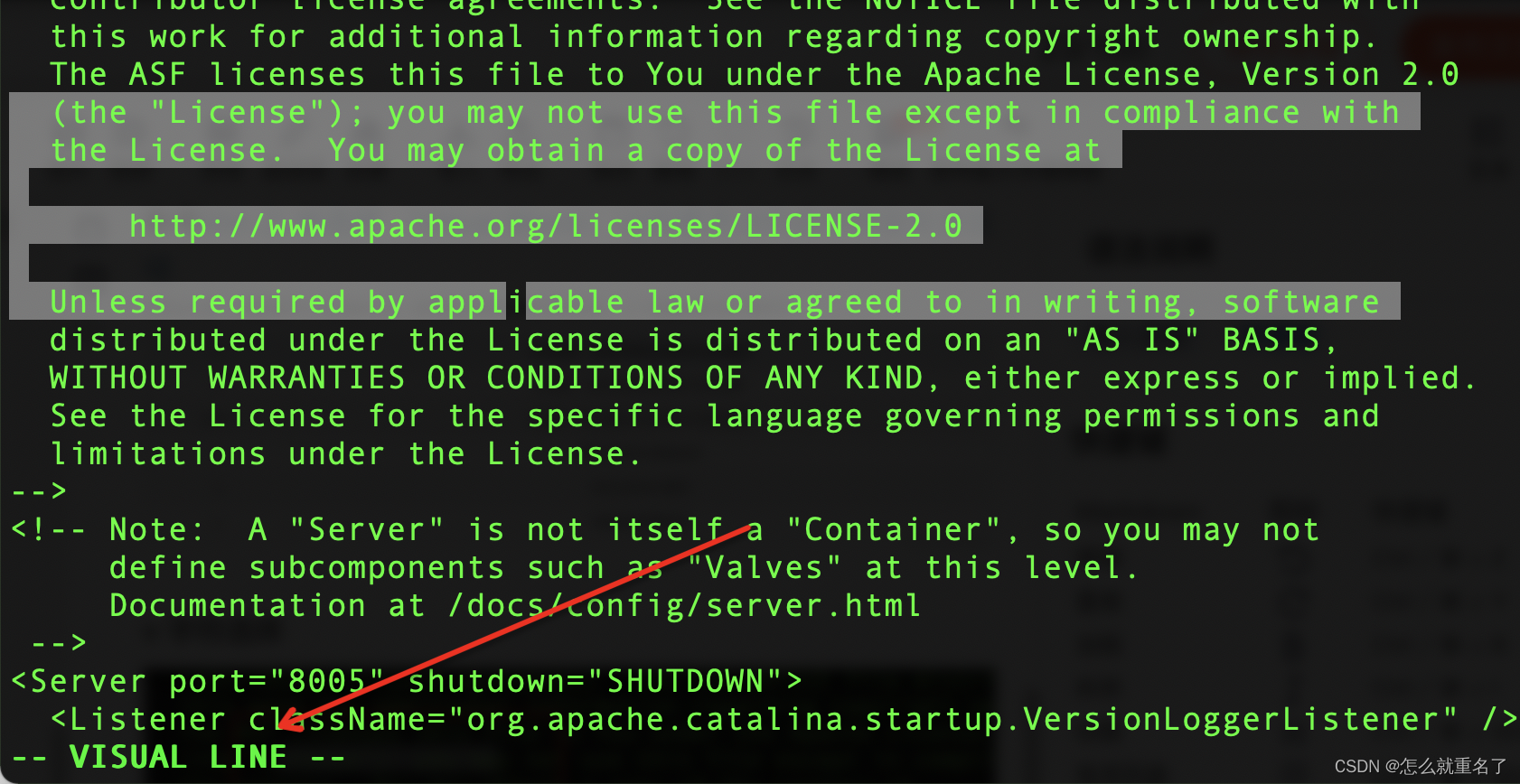
idea+vim+pycharm的块选择快捷键
平时开发的时候,有的时候我们想用矩形框住代码,或者想在某列上插入相同字符 例如下图所示,我想在22-24行的前面插入0000 1. Idea的快捷键:option 鼠标 2. Pycharm的快捷键:shift option 鼠标 2. Vim 块选择 v/V/c…...
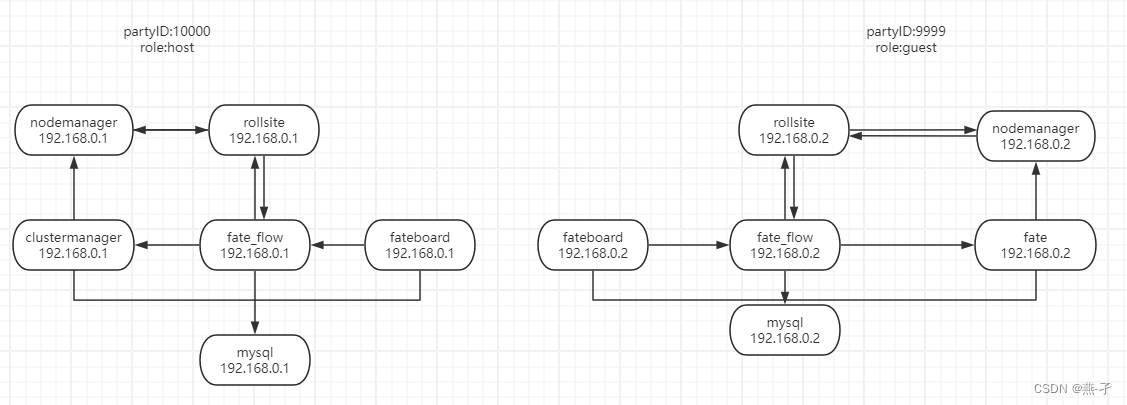
ansible 部署FATE集群单边场景
官方文档: https://github.com/FederatedAI/AnsibleFATE/blob/main/docs/ansible_deploy_FATE_manual.md https://github.com/FederatedAI/AnsibleFATE/blob/main/docs/ansible_deploy_two_sides.md gitee详细文档: docs/ansible_deploy_one_side.md…...

融入Facebook的世界:探索数字化社交的魅力
融入Facebook的世界,是一场数字化社交的奇妙之旅。在这个广袤的虚拟社交空间中,人们可以尽情展现自己、分享生活,与全球朋友、家人和同事保持紧密联系,共同探索社交互动的乐趣与魅力。让我们深入了解这个世界的魅力所在࿱…...
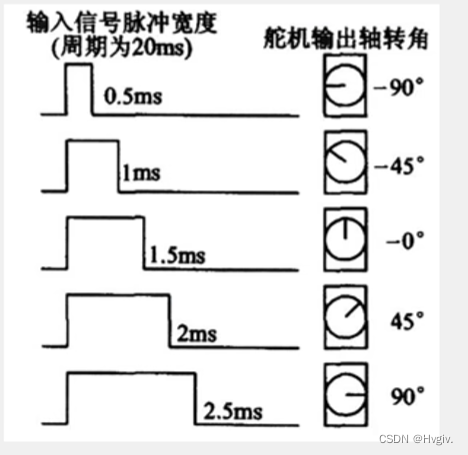
stm32-定时器输出比较PWM
目录 一、输出比较简介 二、PWM简介 三、输出比较模式实现 1.输出比较框图(以通用定时器为例) 2.PWM基本结构 四、固件库实现 1.程序1:PWM呼吸灯 2.程序2:PWM驱动直流电机 3.程序3:控制舵机 一、输出比较简介 死区生成和互补输出一般…...

Redis对过期key的删除策略
假设设置了一批 key 只能存活 1 个小时,那么 1 小时后,redis 是怎么对这批 key 进行删除的? 定期删除 惰性删除 定期删除: redis是默认每隔100ms就随机抽取一些设置了过期时间的key,检查是否过期,如果过期就删除。…...

http的body格式
body数据都通常放在 HTTP 请求的 body 部分。 在 HTTP 请求中,Content-Type 头用于指示 body 中的数据格式。例如,对于 x-www-form-urlencoded 格式的数据,通常会设置 Content-Type: application/x-www-form-urlencoded,而对于 fo…...

Java Web开发从0到1
文章目录 总纲第1章 Java Web应用开发概述1.1 程序开发体系结构1.1.1 C/S体系结构介绍1.1.2 B/S体系结构介绍1.1.3 两种体系结构的比较1.2 Web应用程序的工作原理1.3 Web应用技术1.3.1 客服端应用技术1.3.2 服务端应用技术1.4 Java Web应用的开发环境变量1.5 Tomcat的安装与配置…...

002——编译鸿蒙(Liteos -a)
目录 一、鸿蒙是什么 二、Kconfig 2.1 概述 2.2 编译器 2.3 make使用 本文章引用了很多韦东山老师的教程内容,算是我学习过程中的笔记吧。如果侵权请联系我。 一、鸿蒙是什么 这里我补充一下对鸿蒙的描述 这张图片是鸿蒙发布时使用的,鸿蒙是一个很…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
