十四届蓝桥杯省赛Java B组 合并区域

就是将两个矩阵进行拼接,两矩阵可以旋转90 180 270 度。
因为数据比较小,所以这基本上就是一个大的枚举模拟加搜索,直接暴力求解。
import java.io.*;
import java.util.*;public class Main{static int n;static int N = 101;static int mod = (int)1e9 + 7;static StreamTokenizer stt = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int[][] f = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
// static int[][] ff = {{0, -1, 0}, {0, 0, 1}, {0, 1, 0}, {0, 0, -1}, {1, 0, 0}, {-1, 0, 0}};
// static int[] month = {0, 31,28,31,30,31,30,31,31,30,31,30,31};static int[][] o = new int[N][N];static int[][] p = new int[N][N];static int[][] m = new int[3 * N][3 * N];static int maxi;private static int dfs(int x, int y) {int k = 1;m[x][y] = 0;for(int i = 0; i < 4; i ++) {int nx = x + f[i][0], ny = y + f[i][1];if(nx < 1 || nx > 3 * n || ny < 1 || ny > 3 * n || m[nx][ny] == 0) continue;k += dfs(nx, ny);}return k;}private static void draw(int bx, int by, int[][] o2) {for(int i = bx, ii = 1; ii <= n; ii ++, i ++) {for(int j = by, jj = 1; jj <= n; jj ++, j ++) {m[i][j] = o2[ii][jj];}}}static void asd(int x, int y) throws IOException {// 在地图上画o矩阵draw(n + 1, n + 1, o);// 在地图上画p矩阵draw(x, y, p);// 分别枚举o矩阵和p矩阵所有的1进行深搜for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {int nx = i + n, ny = j + n;if(m[nx][ny] == 1)maxi = Math.max(maxi, dfs(nx, ny));}}for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j++) {int nx = i + x - 1, ny = j + y - 1;if(m[nx][ny] == 1) maxi = Math.max(maxi, dfs(nx, ny));}}}private static void sov() throws IOException {// 在一个三倍大的地图中,枚举p矩阵的坐上角顶点,默认o在中心的n阶矩阵位置for(int i = 1; i <= 2 * n + 1; i ++) {asd(1, i);asd(2 * n + 1, i);asd(i, 1);asd(i, 2 * n + 1);}}static void rotate() {int[][] s = new int[N][N];for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {s[j][n - i + 1] = o[i][j];}}for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {o[i][j] = s[i][j];}}}static void sovle() throws Exception {n = readInt();for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {o[i][j] = readInt();}}for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {p[i][j] = readInt();}}maxi = 0;
// rotate();
// for(int i = 1; i <= n; i ++){
// for(int j = 1; j <= n; j ++) {
// bw.write(o[i][j] + " ");
// }
// bw.write("\n");
// }for(int i = 0; i < 4; i ++) {// 旋转o矩阵rotate();// 拼接两矩阵求解sov();}bw.write(maxi + "\n");}public static void main(String args[]) throws Exception {int t = 1;
// t = Integer.parseInt(br.readLine());
// t = readInt();while((t --) > 0) {
// while((n = Integer.parseInt(br.readLine())) != 0) {sovle();}bw.flush();bw.close();}static int readInt() {try {stt.nextToken();} catch (IOException e) {e.printStackTrace();}return (int)stt.nval;}
}相关文章:

十四届蓝桥杯省赛Java B组 合并区域
就是将两个矩阵进行拼接,两矩阵可以旋转90 180 270 度。 因为数据比较小,所以这基本上就是一个大的枚举模拟加搜索,直接暴力求解。 import java.io.*; import java.util.*;public class Main{static int n;static int N 101;static int mo…...
SpringBoot高级
1.自动配置-Condition Condition是Spring4.0后引入的条件化配置接口,通过实现Condition接口可以完成有条件的加载相应的Bean 进入 SpringBoot 启动类,点击进入 run() 可以看到这个方法是有返回值的,返回值为 ConfigurableApplicationConte…...
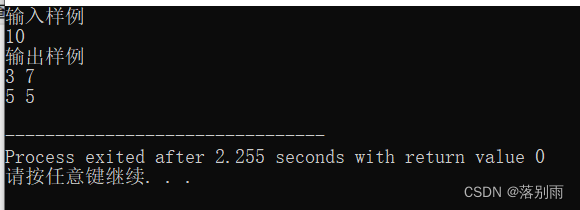
机试:偶数分解
题目描述: 代码示例: #include <bits/stdc.h> using namespace std; int main(){ // 算法思想1:遍历小于该偶数的所有素数,存入数组中,遍历数组找出两个数之和等于偶数的数int n;cout << "输入样例" << endl;cin >> n;int nums[n];int k …...
一周学会Django5 Python Web开发-Jinja3模版引擎-安装与配置
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计35条视频,包括:2024版 Django5 Python we…...

python前端开发
前端开发 快速网站开发 from flask import Flask appFlask(__name__) #创建网址/show/info 和函数index的对应关系, #访问网站,执行index()函数 app.route("/show/info") def index():return "中国联通" if __name__"__main_…...
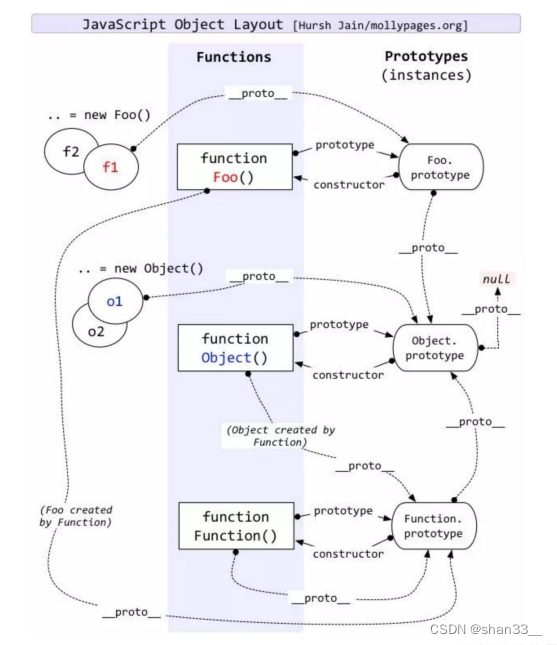
web学习笔记(三十三)
目录 1.严格模式 1.1严格模式的概念: 1.2严格模式在语义上更改的地方: 1.3如何开启严格模式 1.4严格模式应用上的变化 2.原型链 1.严格模式 1.1严格模式的概念: 严格模式有点像es5向es6过渡而产生的一种模式,因为es6的语法…...
flask库
文章目录 flask库1. 基本使用2. 路由路径和路由参数3. 请求跳转和请求参数4. 模板渲染1. 模板变量2. 过滤器3. 测试器 5. 钩子函数与响应对象 flask库 flask是python编写的轻量级框架,提供Werkzeug(WSGI工具集)和jinjia2(渲染模板…...
专业无网设备如何远程运维?向日葵远程控制能源场景案例解析
清洁能源领域,拥有庞大的上下游产业链,涉及的相关工业设备门类多、技术覆盖全、行业应用广。在这一领域内,相关专业设备的供应商的核心竞争力除了本身产品的技术能力之外,服务也是重要的一环。 某企业作为致力于节能环保方向的气…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的稻田虫害检测系统详解(深度学习+Python代码+UI界面+训练数据集)
摘要:本篇文章深入探讨了如何利用深度学习技术开发一个用于检测稻田虫害的系统,并且分享了完整的实现过程和资源代码下载。该系统采用了当前的YOLOv8、YOLOv7、YOLOv6、YOLOv5算法,对其进行了性能对比,包括mAP、F1 Score等关键指标…...

实现upt下客户端用tftp文件传输协议编写客户端发送下载文件
#include <myhead.h> #define SEP_IP #define SEP_PORT int main(int argc, const char *argv[]) {//创建套接字if(int crdsocket(AF_INET,SOCK-DGRAM)-1);{perror("socket error");return -1;}printf("创建成功\n");//填充地址struct sockaddr_in s…...

什么软件可以改ip地址
修改ip地址的软件有哪些,什么软件可以切换电脑手机的ip地址想必很多朋友都在寻找类似的软件,也想知道其中的答案,也能提高自己工作的效率。 经过小编在互联网摸爬滚打这些年,测试认证和整理后,发现一款名叫深度IP转换…...
C#,文字排版的折行问题(Word-wrap problem)的算法与源代码
1、英文的折行问题 给定一个单词序列,以及一行中可以输入的字符数限制(线宽)。 在给定的顺序中放置换行符,以便打印整齐。 假设每个单词的长度小于线宽。 像MS word这样的文字处理程序负责放置换行符。 这个想法是要有平衡的线条。…...

VUE+VScode+elementUI开发环境
0.vue官方文档 你正在阅读的是 Vue 3 的文档! 1.前端准备阶段 VUEVScodeelementUI开发环境 2.Vue外部组件 element-ui 3.angular外部组件 angular-ui 4.教学视频 尚学堂b站视频 5.教学视频配套文档 D:\BaiduNetdiskDownload\025【尚学堂】全新2022版WEB前端为初学者…...
第十四届蓝桥杯省赛真题 Java A 组【原卷】
文章目录 发现宝藏【考生须知】试题 A \mathrm{A} A : 特殊日期试题 B: 与或异或试题 C : \mathrm{C}: C: 平均试题 D: 棋盘试题 E : \mathrm{E}: E: 互质数的个数试题 F: 阶乘的和试题 G: 小蓝的旅行计划试题 H: 太阳试题 I: 高塔试题 J \mathrm{J} J : 反异或 01 串 发现…...
可视化展示与交互编辑:探索3D Web轻量化平台HOOPS WEB Platform在BIM中的新可能性
随着数字技术的飞速发展,建筑行业也在不断迈向数字化转型的道路。在这个过程中,BIM(Building Information Modeling,建筑信息模型)技术已经成为建筑设计、施工和管理领域中的一项重要工具。 而在BIM的应用中ÿ…...

Linux(centos)环境下安装Nginx的步骤文档
在Linux环境下安装Nginx是一个相对直接的过程,本篇文章将提供一个较为通用的安装指南,以及一些可能遇到的问题和解决方案。 目录 一、简介 二、先决条件 三、安装Nginx 1、使用包管理器安装 2、从源代码安装 四、验证安装 五、基本配置 六、常见…...
AI毕业论文降重GPTS,避免AI检测,高效完成论文
视频演示 AI毕业论文降重GPTS,避免AI检测,高效完成论文! 开发目的 “毕业论文降重”GPTS应用,作用为:重新表述学术论文,降低相似性评分,避免AI检测。 使用地址 地址:毕业论文降重…...

什么是线程死锁?形成死锁的四个必要条件是什么?如何避免线程死锁?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 什么是线程死锁 线程死锁是指两个或多个线程由于互相持有对方所需要的资源而无法继续执行的情况。当多个线程同时占用资源,并等待其他线程释放它们所需要…...

webpack一些常用的Loader和Plugin
文章目录 webpack4一些常用的Loader:webpack4一些常用的Plugin:关于webpack5的一些特点:新增特性:修复的问题:内置模块和工具: 关于webpack5的一些内置:内置Loader:内置Plugin: webp…...
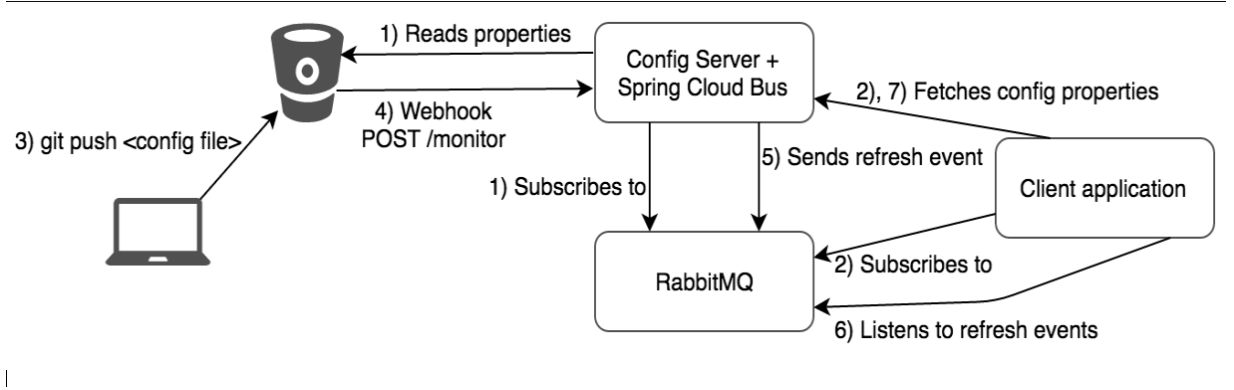
SpringCloud Bus 消息总线
一、前言 接下来是开展一系列的 SpringCloud 的学习之旅,从传统的模块之间调用,一步步的升级为 SpringCloud 模块之间的调用,此篇文章为第八篇,即介绍 Bus 消息总线。 二、概述 2.1 遗留的问题 在上一篇文章的最后,我…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
