函数连续性和Lipschitz连续性
摘要:
直观上,Lipschitz连续性的含义是函数图像的变化速度有一个全局的上限,即函数的增长速率不会无限增加。这种性质确保了函数在任何地方都不会过于陡峭,有助于分析函数的行为,并且在优化、动力系统理论、机器学习等领域有重要应用。例如,在深度学习中,限制神经网络层的Lipschitz常数可以提升模型的泛化能力并稳定训练过程。
1.函数连续性
以下是连续性从最一般到越来越强的要求的几种类型:
1. **连续性(Continuity)**:
- 对于函数 \( f: X \rightarrow Y \) (其中 \( X \) 和 \( Y \) 是拓扑空间),如果对于任意点 \( x_0 \in X \),对所有 \( \epsilon > 0 \),存在一个 \( \delta > 0 \),使得当 \( x \in X \) 满足 \( d_X(x, x_0) < \delta \) 时,有 \( d_Y(f(x), f(x_0)) < \epsilon \),则称函数 \( f \) 在点 \( x_0 \) 处连续。若 \( f \) 在其定义域的所有点都连续,则称其在整个定义域上是连续函数。
2. **局部 Lipschitz 连续性**:
- 函数在某一点或某个区域内满足Lipschitz条件,即存在常数 \( K \) 和该点/区域的一个邻域,在此邻域内函数的变化率不超过 \( K \) 倍的自变量变化。
3. **一致连续性(Uniform Continuity)**:
- 如果函数在它的整个定义域上满足这样的性质:对于任意 \( \epsilon > 0 \),都存在一个 \( \delta > 0 \),使得当对所有的 \( x, y \) 都满足 \( d_X(x, y) < \delta \) 时,就有 \( d_Y(f(x), f(y)) < \epsilon \)。这意味着函数在任何两点之间的变化都能通过控制它们之间的距离来全局地限制。
4. **Lipschitz 连续性**:
- 如前所述,函数 \( f \) 若在其定义域上满足 \( |f(x_1) - f(x_2)| \leq K |x_1 - x_2| \),则称为Lipschitz连续。这是比一致连续更强的形式,它不仅限定了任意两点间的最大变化量,而且这个最大变化量与两点间的距离成比例。
5. **Holder连续性(Hölder Continuity)**:
- 类似于Lipschitz连续性,但允许指数为 \( 0 < \alpha \leq 1 \) 的幂次关系:\( |f(x_1) - f(x_2)| \leq K |x_1 - x_2|^\alpha \)。当 \( \alpha = 1 \) 时,就是Lipschitz连续性。
6. **绝对连续性(Absolutely Continuous)**:
- 在实数区间上的函数 \( f: [a, b] \rightarrow \mathbb{R} \),如果对于任何 \( \epsilon > 0 \),都存在 \( \delta > 0 \),使得对于任意一组互不重叠的闭区间 \( [c_i, d_i] \subset [a, b] \),只要满足 \( \sum_{i} (d_i - c_i) < \delta \),就有 \( \sum_{i} |f(d_i) - f(c_i)| < \epsilon \),则称 \( f \) 在 \( [a, b] \) 上绝对连续。
7. **微分连续性(Differentiable Continuity)**:
- 函数在其定义域内可导意味着它在每一点处都是连续的,并且其导数函数也是连续的,即 \( f \) 在其定义域内的每个点都可微分,且 \( f' \) 是连续函数。
8. **光滑性(Smoothness)**:
- 平滑函数指的是函数及其各阶导数均在定义域内连续,例如 \( C^k \) 或 \( C^\infty \) 类函数,这些函数不仅连续,还可以进行多次微分,具有极高的连续性和结构稳定性。
以上所列各种连续性形式,反映了数学中对函数性质要求逐步提高的过程,也体现了函数行为和变化规律的不同层次理解。
2.Lipschitz连续性
Lipschitz连续性(也称为Lipschitzian continuity)是数学分析中的一种强于均匀连续的函数连续性条件,它以德国数学家Rudolf Lipschitz的名字命名。对于一个函数f定义在度量空间X到Y之间(通常X和Y是实数向量空间或者更一般的赋范向量空间),如果存在一个正常数K(称为Lipschitz常数),使得对任意x和y属于X有:
\[ |f(x) - f(y)| \leq K \cdot d(x, y) \]
其中\(d(x, y)\)表示X中的两点x和y之间的距离,则称函数f在X上满足Lipschitz条件或具有Lipschitz连续性。
简单来说,这意味着函数值的变化幅度与输入变量的变化幅度之间有一个固定的比例关系。直观上,这表明函数图像在任何地方都不会陡峭到无限的程度,从而为函数的行为提供了强有力的局部约束。
函数 \( f \) 在度量空间 \( X \) 上满足Lipschitz条件或具有Lipschitz连续性意味着对于任意在 \( X \) 中的两个点 \( x_1 \) 和 \( x_2 \),它们经过函数 \( f \) 映射后,在目标空间中的距离与它们在 \( X \) 中的距离之间存在一个固定的比例关系,这个比例由一个正常数 \( K \)(称为Lipschitz常数)来控制。具体表述为:
\[ |f(x_1) - f(x_2)| \leq K \cdot d_X(x_1, x_2) \]
其中 \( d_X(x_1, x_2) \) 表示在度量空间 \( X \) 中点 \( x_1 \) 和 \( x_2 \) 之间的距离。
直观上,Lipschitz连续性的含义是函数图像的变化速度有一个全局的上限,即函数的增长速率不会无限增加。这种性质确保了函数在任何地方都不会过于陡峭,有助于分析函数的行为,并且在优化、动力系统理论、机器学习等领域有重要应用。例如,在深度学习中,限制神经网络层的Lipschitz常数可以提升模型的泛化能力并稳定训练过程。
在机器学习、优化理论以及微分方程等领域,Lipschitz连续性有着广泛的应用,例如:
- 在非线性优化中,梯度具有Lipschitz连续性质意味着算法可能具备全局收敛的保证。
- 在生成对抗网络(GANs)的设计中,限制鉴别器的Lipschitz连续性有助于训练过程的稳定性和生成样本的质量。
- 在动态系统理论中,Lipschitz连续的函数可以确保相关的微分方程解的存在唯一性等。
3.非线性优化中梯度的Lipschitz连续性
在非线性优化中,梯度具有Lipschitz连续性质意味着算法可能具备全局收敛的保证。
在非线性优化中,如果目标函数的梯度(或雅可比矩阵)具有Lipschitz连续性,这意味着梯度的变化率有一个全局上界。具体来说,对于一个多元函数 \( f: \mathbb{R}^n \rightarrow \mathbb{R} \),若其梯度 \( \nabla f(x) \) 满足:
\[ ||\nabla f(x_1) - \nabla f(x_2)|| \leq L ||x_1 - x_2|| \]
其中 \( L \) 是常数,表示梯度的Lipschitz常数,那么我们说梯度 \( \nabla f \) 具有Lipschitz连续性。
这种性质对优化算法的设计和分析有着重要意义,特别是在设计迭代方法时。例如,在一些优化算法如梯度下降法、牛顿法以及它们的变种中,如果目标函数的梯度满足Lipschitz条件,则可以证明算法至少能在局部区域收敛到稳定点,甚至在某些条件下能够保证全局收敛。这是因为Lipschitz连续性有助于确保搜索方向的稳定性,并且能提供关于算法步长选择的合理依据,从而避免了因梯度变化过快而导致的不稳定性问题。
相关文章:

函数连续性和Lipschitz连续性
摘要: 直观上,Lipschitz连续性的含义是函数图像的变化速度有一个全局的上限,即函数的增长速率不会无限增加。这种性质确保了函数在任何地方都不会过于陡峭,有助于分析函数的行为,并且在优化、动力系统理论、机器学习等…...
Qt 鼠标滚轮示例
1.声明 void wheelEvent(QWheelEvent *event) override;2.实现(方便复制、测试起见用静态变量) #include <mutex> void MainWindow::wheelEvent(QWheelEvent *event) {static QLabel *label new QLabel("Zoom Level: 100%", this);st…...
【Unity】进度条和血条的三种做法
前言 在使用Unity开发的时候,进度条和血条是必不可少的,本篇文章将简单介绍一下几种血条的制作方法。 1.使用Slider Slider组件由两部分组成:滑动区域和滑块。滑动区域用于显示滑动条的背景,而滑块则表示当前的数值位置。用户可…...
多人聊天室 (epoll - Linux网络编程)
文章目录 零、效果展示一、服务器代码二、客户端代码三、知识点1.connect()2.socket()3.bind()4.send()5.recv() 四、改进方向五、跟练视频 零、效果展示 一个服务器作为中转站,多个客户端之间可以相互通信。至少需要启动两个客户端。 三个客户端互相通信 一、服务…...
vite配置
"vite": "^5.1.4" resolve.alias:配置别名 1、执行npm install -D types/node 或者 yarn add types/node -D 2、以下配置代表访问src时可以用“”代替 resolve: {alias: {"": path.resolve(__dirname, "./src"),},}, 使…...

服务器生产环境问题解决思路
游戏服务器开发节奏比较快,版本迭代很频繁,有一些项目甚至出现了周更新(每周准时停服更新维护)。由于功能开发时间短,研发人员本身技术能力等原因,线上出现bug很常见。笔者经历过的游戏项目,一年到头没几次更新不出现bug的(当然,配置问题也算bug)。那当出现bug,我们…...

鸿蒙Harmony应用开发—ArkTS声明式开发(容器组件:Column)
沿垂直方向布局的容器。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 可以包含子组件。 接口 Column(value?: {space?: string | number}) 从API version 9开始,该接口…...
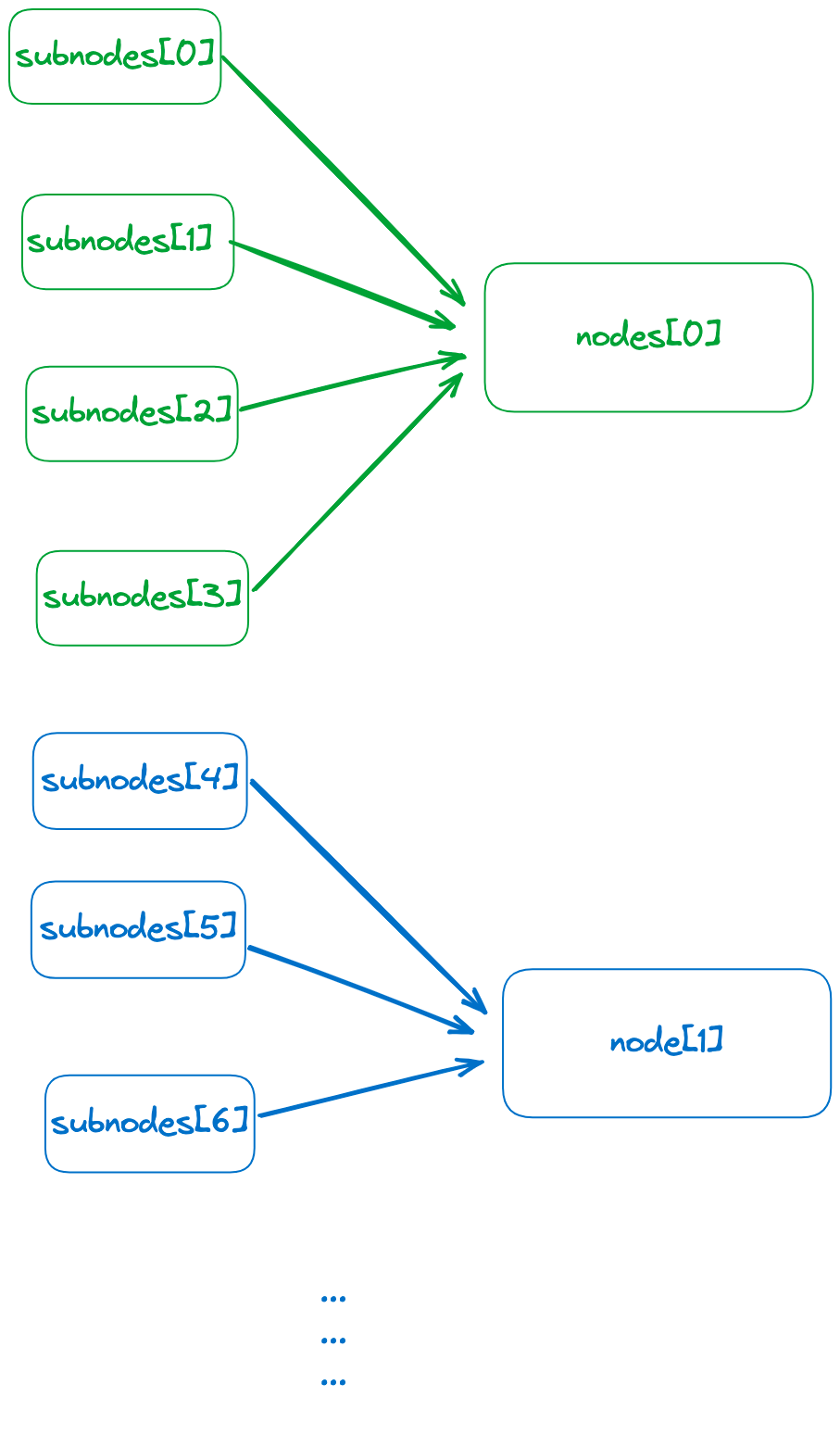
LLM之RAG实战(三十)| 探索RAG语义分块策略
在LLM之RAG实战(二十九)| 探索RAG PDF解析解析文档后,我们可以获得结构化或半结构化的数据。现在的主要任务是将它们分解成更小的块来提取详细的特征,然后嵌入这些特征来表示它们的语义,其在RAG中的位置如图1所示&…...

软件测试-------Web(性能测试 / 界面测试 / 兼容性测试 / 安全性测试)
Web(性能测试 / 界面测试 / 兼容性测试 / 安全性测试) 一、Web性能测试:(压力测试、负载测试、连接速度测试)1、压力测试: 并发测试 (如500人同时登录邮箱) 2、负载测试…...
)
工欲善其事,必先利其器,Markdown和Mermaid的梦幻联动(2)
该文章Github地址:https://github.com/AntonyCheng/typora-notes/tree/master/chapter03-mermaid 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文…...

STM32基础--使用寄存器点亮流水灯
GPIO 简介 GPIO 是通用输入输出端口的简称,简单来说就是 STM32 可控制的引脚,STM32 芯片的 GPIO 引脚与外部设备连接起来,从而实现与外部通讯、控制以及数据采集的功能。STM32 芯片的 GPIO被分成很多组,每组有 16 个引脚…...
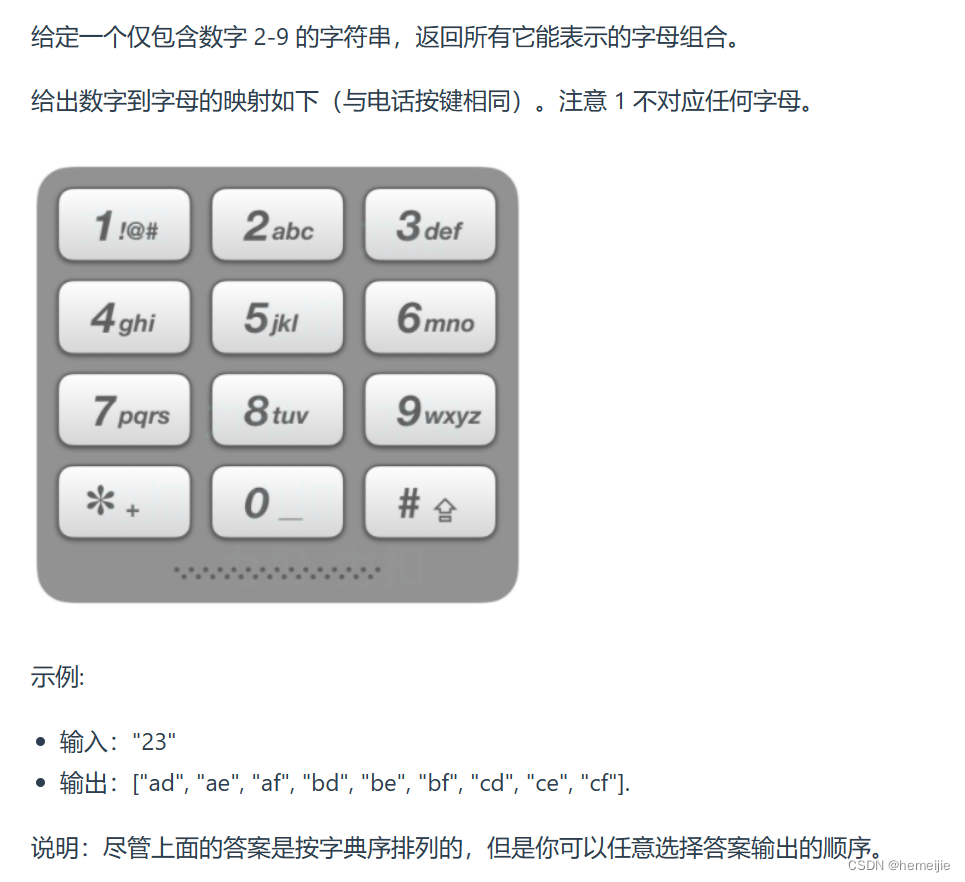
代码随想录训练营Day25:● 216.组合总和III ● 17.电话号码的字母组合
216.组合总和III 题目链接 https://leetcode.cn/problems/combination-sum-iii/description/ 题目描述 思路 自己写的效率会慢一些,而且没有用到剪枝 class Solution {List<List<Integer>> list new ArrayList<>();List<Integer> lis…...

SwiftUI的 特性 - ViewModify
SwiftUI的 特性 - ViewModify 记录一下SwiftUI的 特性 - ViewModify的使用方式 可以通过viewModify来管理视图的样式,结合extension来完成封装达到解偶效果 import SwiftUI/// 我们可以通过viewModify来管理视图的样式,来达到解偶效果 struct DefaultB…...
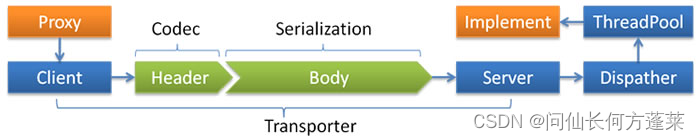
中间件 | RPC - [Dubbo]
INDEX 1 Dubbo 与 web 容器的关系2 注册发现流程3 服务配置3.1 注册方式 & 订阅方式3.2 服务导出3.3 配置参数 4 底层技术4.1 Dubbo 的 spi 机制4.2 Dubbo 的线程池4.3 Dubbo 的负载均衡策略4.3 Dubbo 的协议 1 Dubbo 与 web 容器的关系 dubbo 本质上是一个 RPC 框架&…...

【中等】保研/考研408机试-二叉树相关
目录 一、基本二叉树 1.1结构 1.2前序遍历(注意三种遍历中Visit所在的位置) 1.2中序遍历 1.3后序遍历 二、真题实战 2.1KY11 二叉树遍历(清华大学复试上机题)【较难】 2.2KY212 二叉树遍历二叉树遍历(华中科技大…...
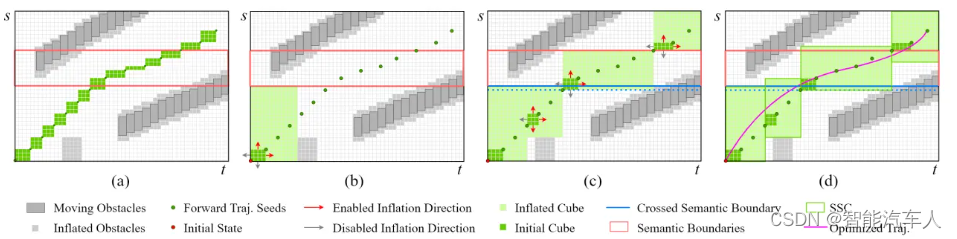
自动驾驶---Motion Planning之构建SLT Driving Corridor
1 背景 在上篇博客《自动驾驶---Motion Planning之Speed Boundary》中,主要介绍了Apollo中Speed Boundary的一些内容,可以构造ST图得到边界信息,最后结合粗糙的速度曲线和路径曲线,即可使用优化的方法求解得到最终的轨迹信息(s,s,s,l,l,l)。 本篇博客笔者主要介绍近…...
本地文件包含漏洞利用
目录 前期信息收集获取网站权限获取服务器权限纵向提权 前期信息收集 拿到目标的资产,先试一下IP能不能访问 探测一下目标的端口运行的是什么服务 nmap -sC -sV xx.xx9.95.185 -Pn获取网站权限 我们可以知道目标的80端口上运行着http服务,服务器是u…...
【docker】docker的常用命令
📝个人主页:五敷有你 🔥系列专栏:中间件 ⛺️稳中求进,晒太阳 常规命令 docker version #查看docker 版本信息docker info #显示docker 的系统信息,包括镜像和容器数量docker --help #查看所有的命…...

jmeter实战
jmeter学习 1,接口在定义时,post请求参数尽量放在body里面,get请求参数尽量放在parameters里面,否则会导致jmeter请求接口报错的问题(jmeter底层有较为严格的请求格式) 2,定义全局变量使用:Config Elemen…...

面试官常问问题
1、请你简单的自我介绍一下? 【Tips】① 口述内容不可与简历内容冲突;②阐述方式避免过度官方 且语速较快;③言简意赅,直击要害,抓重点突出项;④面试前应自己模拟练习几次,避免过度紧张导致的口…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
李沐--动手学深度学习--GRU
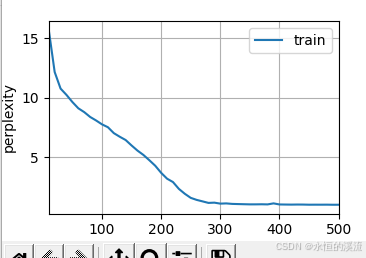
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
