这是二叉搜索树吗?
一棵二叉搜索树可被递归地定义为具有下列性质的二叉树:对于任一结点,
- 其左子树中所有结点的键值小于该结点的键值;
- 其右子树中所有结点的键值大于等于该结点的键值;
- 其左右子树都是二叉搜索树。
所谓二叉搜索树的“镜像”,即将所有结点的左右子树对换位置后所得到的树。
给定一个整数键值序列,现请你编写程序,判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果。
输入格式:
输入的第一行给出正整数 N(≤1000)。随后一行给出 N 个整数键值,其间以空格分隔。
输出格式:
如果输入序列是对一棵二叉搜索树或其镜像进行前序遍历的结果,则首先在一行中输出 YES ,然后在下一行输出该树后序遍历的结果。数字间有 1 个空格,一行的首尾不得有多余空格。若答案是否,则输出 NO。
输入样例 1:
7
8 6 5 7 10 8 11
输出样例 1:
YES
5 7 6 8 11 10 8
输入样例 2:
7
8 10 11 8 6 7 5
输出样例 2:
YES
11 8 10 7 5 6 8
输入样例 3:
7
8 6 8 5 10 9 11
输出样例 3:
NO代码:
#include<bits/stdc++.h>
using namespace std;
struct Node{int data;Node *l;Node *r;
};
vector<int>s,pre1,pre2,post1,post2;//先构造树
Node *build(Node *root,int x){if(root==NULL){root = new Node;root->l = root->r = NULL;root->data = x;}else if(x<root->data){ //小于根节点说明是左子树 root->l = build(root->l,x);}else{ //大于根节点说明是右子树 root->r = build(root->r,x);}return root;
} void preorder1(Node *root){ //前序遍历(根左右) if(root==NULL){return;}pre1.push_back(root->data);preorder1(root->l);preorder1(root->r);
}
void preorder2(Node *root){ //前序遍历的逆遍历(根右左) if(root==NULL){return;}pre2.push_back(root->data);preorder2(root->r);preorder2(root->l);
}
void postorder1(Node *root){ //后序遍历(左右根) if(root==NULL){return;}postorder1(root->l);postorder1(root->r);post1.push_back(root->data);
}
void postorder2(Node *root){ //后序遍历的逆遍历(右左根) if(root==NULL){return;}postorder2(root->r);postorder2(root->l);post2.push_back(root->data);
}
int main(){int n;cin>>n;Node *root = NULL;for(int i = 0;i<n;i++){int t;cin>>t;root = build(root,t);s.push_back(t);}preorder1(root); //进行前序遍历 if(s!=pre1){ //如果不是前序遍历就进行前序遍历的逆遍历 preorder2(root);if(s!=pre2){ //如果也不是前序遍历的逆遍历就输出NO cout<<"NO";}else{ //如果是前序遍历的逆遍历就输出YES cout<<"YES"<<endl;postorder2(root); //进行后序遍历的逆遍历然后输出 for(int i = 0;i<n;i++){cout<<post2[i];if(i!=n-1){cout<<" ";}}}}else{ //如果是前序遍历就输出YES cout<<"YES"<<endl;postorder1(root); //进行后序遍历然后输出 for(int i = 0;i<n;i++){cout<<post1[i];if(i!=n-1){cout<<" ";} }}
}
相关文章:

这是二叉搜索树吗?
一棵二叉搜索树可被递归地定义为具有下列性质的二叉树:对于任一结点, 其左子树中所有结点的键值小于该结点的键值;其右子树中所有结点的键值大于等于该结点的键值;其左右子树都是二叉搜索树。 所谓二叉搜索树的“镜像”…...

5.82 BCC工具之tcpdrop.py解读
一,工具简介 tcpdrop工具打印被内核丢弃的 TCP 数据包或段的详细信息,包括导致丢弃的内核堆栈跟踪。 当网络出现拥堵、资源不足或其他原因导致数据包被内核丢弃时,tcpdrop可以帮助开发者和网络管理员识别并定位问题。 该工具通过钩住内核中处理TCP数据包的相关函数,捕获…...

JavaScript 基础知识
一、初识 JavaScript 1、JS 初体验 JS 有3种书写位置,分别为行内、内部和外部。 示例: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"wid…...

【判断是否为回文数】
法一:用字符串形式判断(依次对比前面和后面的数是否相等) #include<stdio.h> #include<string.h> int main() {char st[100];scanf("%s",st);int flag1,nstrlen(st);for(int i0,jn-1;i<n,j>0;i,j--){if(st[i]!…...
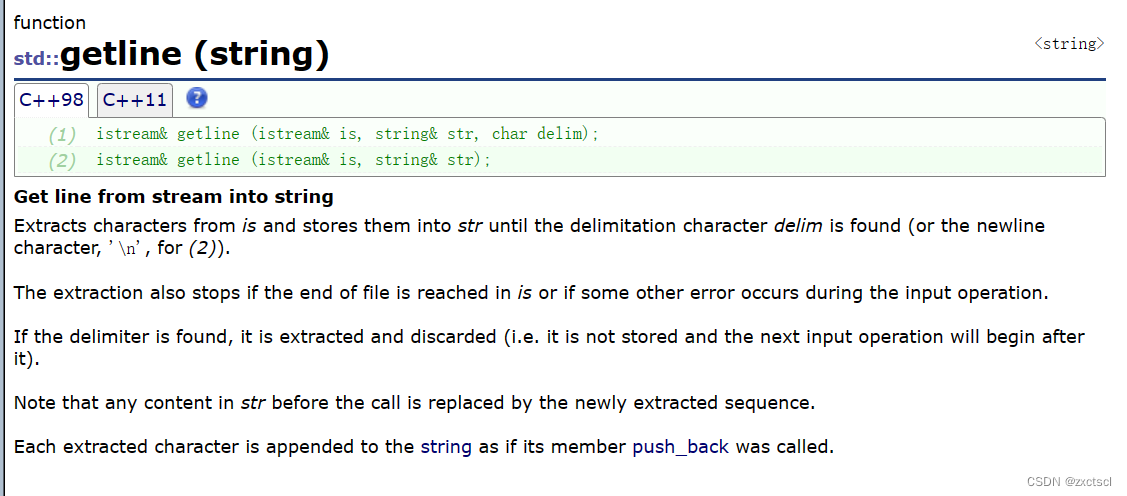
【C++】string进一步介绍
个人主页 : zxctscl 如有转载请先通知 文章目录 1. 前言2. 迭代器2.1 反向迭代器2.2 const对象迭代器 3. Capacity3.1 size和length3.2 max_size3.3 capacity3.4 clear3.5 shrink_to_fit (了解即可)3.6 reserve3.7 resize 4. Element access4…...

思科设备下面主机访问公网经常时好时坏延迟大丢包不稳定
环境: 思科防火墙ASA5555 Cisco Adaptive Security Appliance Software Version 9.4(2)6 Device Manager Version 7.5(2)153 内外为DMZ区域 思科交换机(C3560E-UNIVERSALK9-M), Version 12.2(55)SE5 主机 centos 7 问题描述: 思科设备下面主机访问公网经常时好时坏不稳定…...

nuxtjs 如何通过ecosystem.config.js配置pm2?
在 Nuxt.js 项目中,您可以通过 ecosystem.config.js 文件来配置 PM2,以便使用 PM2 来管理 Nuxt.js 应用的进程。ecosystem.config.js 是一个特殊的配置文件,它允许您定义应用的各种属性,如脚本路径、环境变量、日志设置等。 下面…...
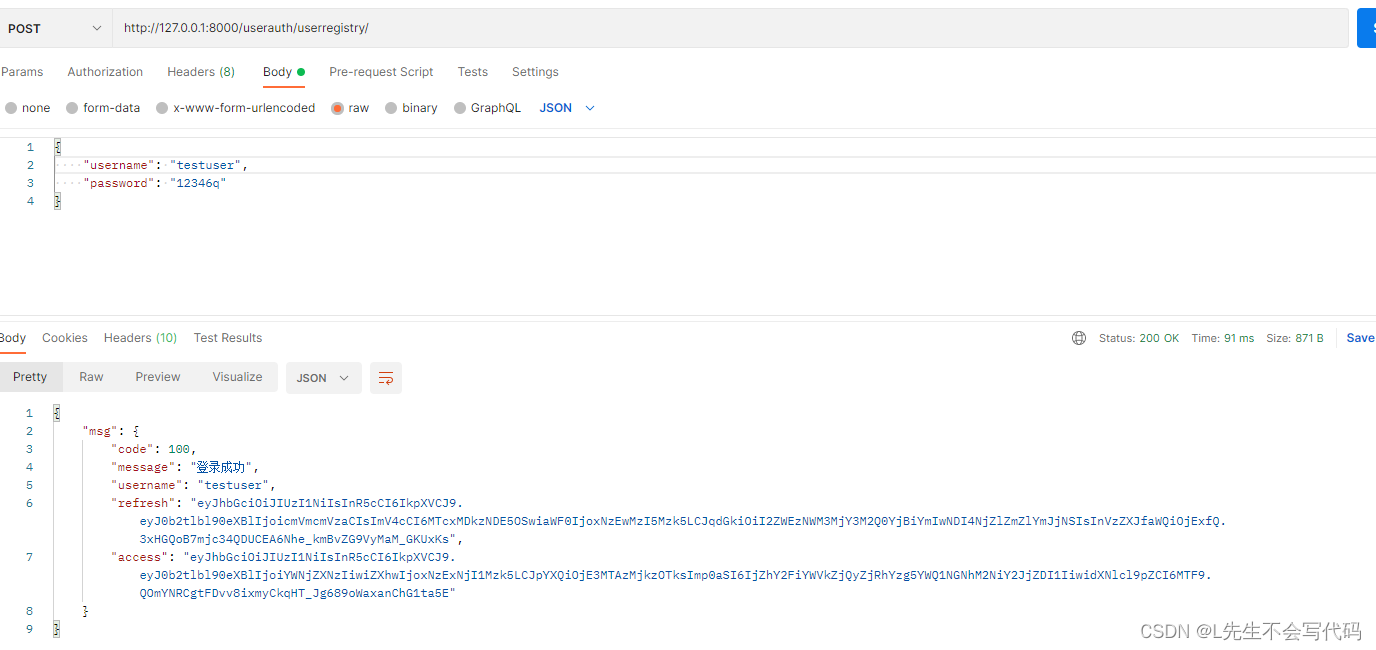
个人博客系列-后端项目-用户注册功能(7)
介绍 用户注册API的主要流程:1.前端用户提交用户名,密码 2. 序列化器校验用户名,密码是否合法。3.存入数据库。4.签发token 创建序列化器 from rest_framework import serializers from rest_framework_simplejwt.serializers import Toke…...
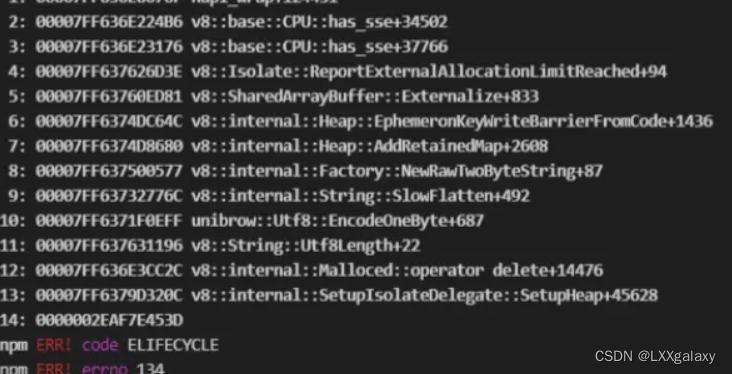
vue项目因内存溢出启动报错
前端能正常启动,但只要一改动就报错启动出错。 解决办法: 安装依赖 npm install cross-env increase-memory-limit 然后再做两件事:在node 在package.json 里的 script 里进行配置 LIMIT是你想分配的内存大小,这里的8192单位…...

UI 学习 二 可访问性 模式
教程:Accessibility – Material Design 3 一 颜色对比 颜色和对比度可以用来帮助用户看到和理解应用程序的内容,与正确的元素交互,并理解操作。 颜色可以帮助传达情绪、语气和关键信息。可以选择主色、辅助色和强调色来支持可用性。元素之…...
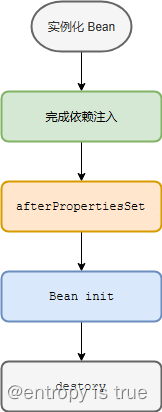
Spring学习
Maven 的配置文件是一个强约定的XML格式文件,它的文件名一定是pom.xml。 1、POM (Project Object Model) 一个 Java 项目所有的配置都放置在 POM 文件中,大概有如下的行为: 定义项目的类型、名字管理依赖关系定制插件的 1.maven坐标 <…...

鸿蒙开发-UI-动画-组件内转场动画
鸿蒙开发-UI-组件3 鸿蒙开发-UI-气泡/菜单 鸿蒙开发-UI-页面路由 鸿蒙开发-UI-组件导航-Navigation 鸿蒙开发-UI-组件导航-Tabs 鸿蒙开发-UI-图形-图片 鸿蒙开发-UI-图形-绘制几何图形 鸿蒙开发-UI-图形-绘制自定义图形 鸿蒙开发-UI-图形-页面内动画 文章目录 前言 一、基本概…...

Leet code 179 最大数
解题思路 贪心算法 贪心算法就是走一步看一步 每一步都取当前位置的最优解 这题我们该如何贪呢? 我们先把int数组转换为string数组 以示例2为例 3 30 34 5 9 排序哪个在前哪个在后? 3 30 (330)> 30 3 (30…...

swagger踩坑之请求类不显示具体字段
swagger踩坑之请求类不显示具体字段 省流:枚举字段需要加上ApiModelProperty注解 过程复现: TestEnum 枚举不加注解,swagger的UI类不显示详细字段 Data Accessors(chain true) ApiModel(value "test对象", description &quo…...
案例分析篇14:信息系统安全设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...

前端之用HTML弄一个古诗词
将进酒 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>将进酒</title><h1><big>将进酒</big> 君不见黄河之水天上来</h1><table><tr><td ><img…...

Linux 安装使用 Docker
目录 一、前提卸载命令:执行情况: 二、安装 Docker1. 通过仓库进行安装(在线方式)1.1 设置存储库1.2 查看可安装版本1.3 安装 Docker1.4 启动 Docker1.5 验证是否成功 2. 通过 RMP 包安装(离线方式)2.2 安装…...
Doris部署学习(一)
目录 前言 一、Docker容器支持 二、Doris编译步骤 1.拉取镜像 2.构建Docker编译容器 3.下载源码并编译 前言 本文档主要介绍如何通过源码在Docker编译 Doris,以及部署。 一、Docker容器支持 Docker教程:Docker & Docker-Compose 安装教程 - 知…...

QT下跨平台库实现及移植经验分享
最近在移植公司一个QT桌面软件到android上,有一些公司自定义的库,用了很多windows的api,移植过程很是曲折,在此有一些感悟分享一下~ 一.自编写跨平台库 1.有时候为了程序给第三方用需要编译一些qt封装库,并可能跨平台…...
8:00面试,8:06就出来了,问的问题有点变态。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到9月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
