C#求水仙花数
目录
1.何谓水仙花数
2.求三位数的水仙花数
3.在遍历中使用Math.DivRem方法再求水仙花数
1.何谓水仙花数
水仙花数(Narcissistic number)是指一个 n 位正整数,它的每个位上的数字的 n 次幂之和等于它本身。例如,153 是一个 3 位数,它的每个位上的数字的 3 次幂之和为 1^3+5^3+3^3=153,因此 153 是一个水仙花数。
水仙花数得名于希腊神话中的美少年纳西索斯(Narcissus),他因为爱上自己的倒影而化为水仙花。在数学中,水仙花数是一种具有特定性质的数字,这种性质类似于纳西索斯对自身的迷恋。
水仙花数在数学上并不常见,但在一些数学问题和谜题中可能会出现。例如,有人可能会要求找出所有三位数的水仙花数,或者找出所有 n 位数的水仙花数。这些问题可以通过编程和数学方法解决,但通常需要一定的计算和推理能力。
2.求三位数的水仙花数
// 求三位数的水仙花数
namespace _148
{class NarcissisticNumber{static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);for (int i = 100; i < 1000; i++){if (IsNarcissistic(i)){Console.WriteLine(i);}}}/// <summary>/// 这个水仙花数算法的实现很巧妙/// </summary>static bool IsNarcissistic(int number){int sum = 0;int temp = number;while (temp > 0) {int digit = temp % 10;sum += digit * digit * digit;temp /= 10;}return sum == number;}}
}
//运行结果:
/*
153
370
371
407*/
这段代码首先使用一个循环遍历 100 到 999 之间的所有三位数。对于每个数字,它调用 IsNarcissistic 函数来检查该数字是否为水仙花数。如果是,它将该数字输出到控制台。IsNarcissistic 函数计算给定数字的每个位上的数字的三次幂的和,以检查它是否为水仙花数。如果求和结果等于原始数字,则该数字是水仙花数,函数返回 true;否则,它返回 false。
3.在遍历中使用Math.DivRem方法再求水仙花数
换个思维,在遍历中使用Math.DivRem方法再求水仙花数,然后,再把找到的水仙花数输出到ListBox控件。
// 求解水仙花数
namespace _148_1
{public partial class Form1 : Form{private Label? label1;private ListBox? listBox1;private Button? button1;public Form1(){InitializeComponent();StartPosition = FormStartPosition.CenterScreen;Load += Form1_Load;}private void Form1_Load(object? sender, EventArgs e){// // label1// label1 = new Label{AutoSize = true,ForeColor = SystemColors.ActiveCaptionText,Location = new Point(12, 9),Name = "label1",Size = new Size(43, 17),TabIndex = 0,Text = "水仙花数的算法是一个三位数,每一位数的立方相" + "\r" + "加等于该数本身。",};// // listBox1// listBox1 = new ListBox{FormattingEnabled = true,ItemHeight = 17,Location = new Point(12, 43),Name = "listBox1",Size = new Size(270, 72),TabIndex = 1};// // button1// button1 = new Button{ForeColor = SystemColors.ActiveCaptionText,Location = new Point(207, 121),Name = "button1",Size = new Size(75, 23),TabIndex = 2,Text = "计算",UseVisualStyleBackColor = true};button1.Click += Button1_Click;// // Form1// AutoScaleDimensions = new SizeF(7F, 17F);AutoScaleMode = AutoScaleMode.Font;ClientSize = new Size(294, 156);Controls.Add(button1);Controls.Add(listBox1);Controls.Add(label1);ForeColor = SystemColors.ControlLightLight;Name = "Form1";Text = "求水仙花数";}private void Button1_Click(object? sender, EventArgs e){listBox1!.Items.Clear();for (int i = 100; i < 1000; i++){int a = i / 100;Math.DivRem(i, 100, out int b); //获取3位数中的后两位数b /= 10; //获取3位数中的第二位数Math.DivRem(i, 10, out int c); //获取3位数中的第3位数a = a * a * a; //计算第一位数的立方b = b * b * b; //计算第二位数的立方c = c * c * c; //计算第3位数的立方if ((a + b + c) == i) //如果符合水仙花数listBox1.Items.Add(i.ToString());//显示当前3位数}}}
}

相关文章:

C#求水仙花数
目录 1.何谓水仙花数 2.求三位数的水仙花数 3.在遍历中使用Math.DivRem方法再求水仙花数 1.何谓水仙花数 水仙花数(Narcissistic number)是指一个 n 位正整数,它的每个位上的数字的 n 次幂之和等于它本身。例如,153 是一个 3 …...
FFmpeg转码参数说明及视频转码示例
-b : 设置音频或者视频的转码码率 -b:v 只设置视频码率 -b:a 只设置音频码率 -ab: 只设置音频码率, 默认码率大小为: 128k bit/s -g: 设置视频GOP大小,表示I帧之间的间隔,默认为12 -ar: 设置音频采样率,默认0 -ac: 设置音频通道数量 默认0 -bf: 设置连…...

qiankun:vite/webpack项目配置
相关博文: https://juejin.cn/post/7216536069285429285?searchId202403091501088BACFF113F980BA3B5F3 https://www.bilibili.com/video/BV12T411q7dq/?spm_id_from333.337.search-card.all.click qiankun结构: 主应用base:vue3historyv…...

【Linux】深入了解Linux磁盘配额:限制用户磁盘空间的利器
🍎个人博客:个人主页 🏆个人专栏:Linux ⛳️ 功不唐捐,玉汝于成 前言 在多用户环境下管理磁盘空间是服务器管理中的一项重要任务。Linux提供了强大的磁盘配额功能,可以帮助管理员限制用户或组对文件系统…...

Kamailio Debian安装
新方法是: apt install -y gnupg2 wget -O- https://deb.kamailio.org/kamailiodebkey.gpg | gpg --dearmor | tee /usr/share/keyrings/kamailio.gpg 老方法是: apt install -y gnupg2 wget -O- http://deb.kamailio.org/kamailiodebkey.gpg | apt-key…...
)
web学习笔记(三十四)
目录 1.面向对象的特征 2.面向对象的继承方式 3.正则表达式 3.1如何创建正则表达式 3.2边界符 3.2[ ]方括号 3.3正则表达式中相关的方法汇总 1.面向对象的特征 封装性:就像是把东西放在一个密封的盒子里一样,只让外部使用者通过指定的接口来访…...

2024/03/16----面试中遇到的一些面试题
1.请简单的说一下IOC,AOP 1.1 IOC 控制反转(IOC)是一种设计思想,就是将原本在程序中需要手动创建对象,现在交由Spring管理创建,从而降低代码之间的耦合度。 IoC 最常见以及最合理的实现方式叫做依赖注入…...

【SysBench】Linux 安装 sysbench-1.20
安装目的是为了对 MySQL 8.0.x 、PostgreSQL 进行基准测试。 0、sysbench 简介 sysbench 是一个可编写脚本的多线程基准测试工具,基于 LuaJIT 。 它最常用于数据库基准测试,但也可以 用于创建任意不涉及数据库服务器的复杂工作负载。 sysbench 附带以…...

设计模式 — — 代理模式
一、是什么 代理模式(Proxy Pattern)是为一个对象提供一个代用品或占位符,以便控制对它的 生活场景: 租房、买房,比如链家等房屋中介机构,起到的作用就是代理 二、使用 const proxy new Proxy(target, …...
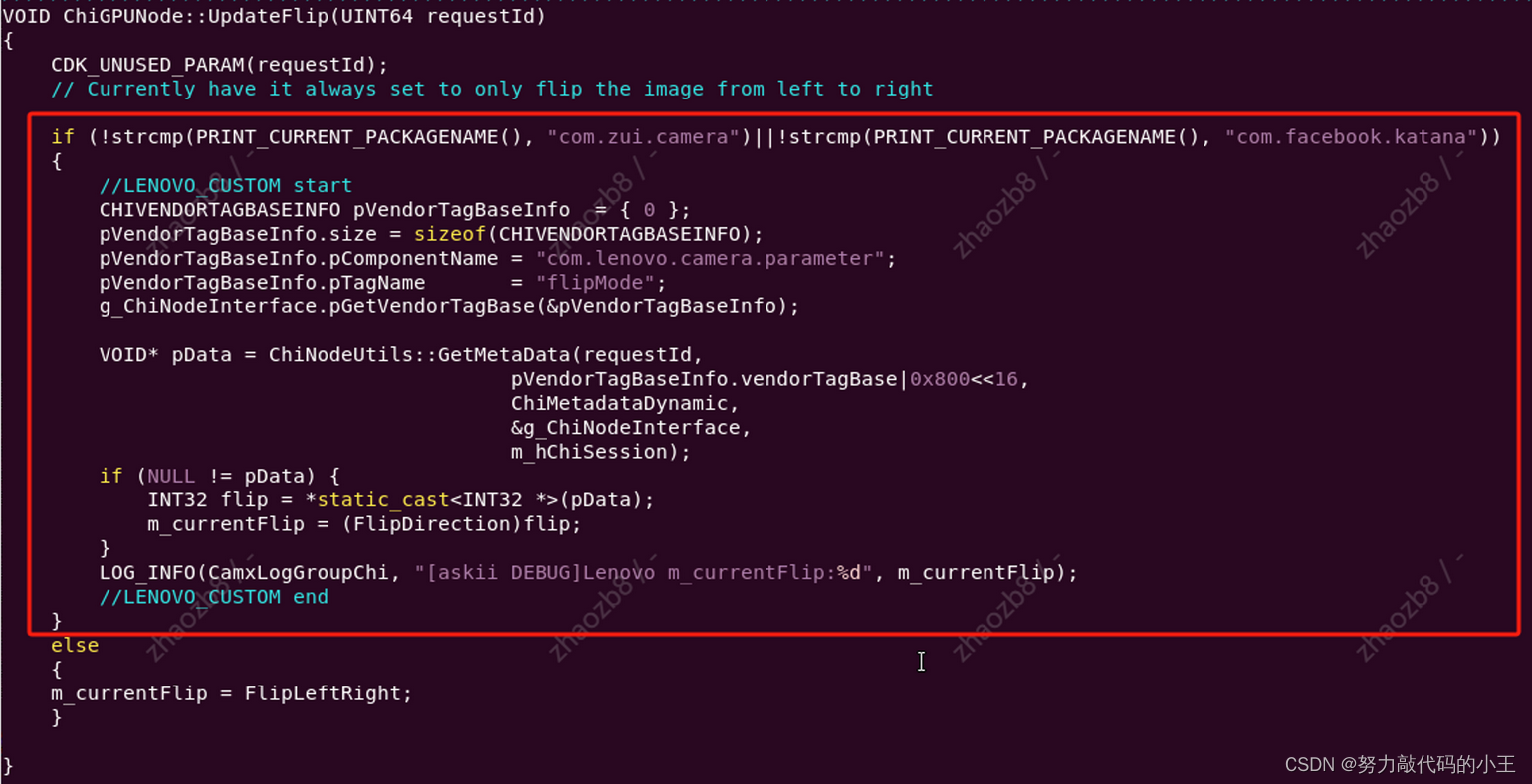
【高通camera hal bug分析】高通自带相机镜像问题
首先打了两个log,一个是开启镜像的log,还有一个是没有开启镜像的log,如果我们开启镜像以后,观察开启镜像log发现 , 这段代码走的没有任何问题,因为Flip的值等于1了。 关闭镜像log如下: 如果我们不开启镜像…...

EPICS和Arduino Uno之间基于串行文本协议的控制开发
Arduino Uno的串口服务程序设置如文本的串口通信协议设计以及在Arduino上的应用-CSDN博客中所示。通过在串口上发送约定的文本协议,它实现的功能如下: 实现功能: 读取三路0.0V~5.0V模拟量输入,读取端口A0~A2设置三路0.0V~5.0V的模…...
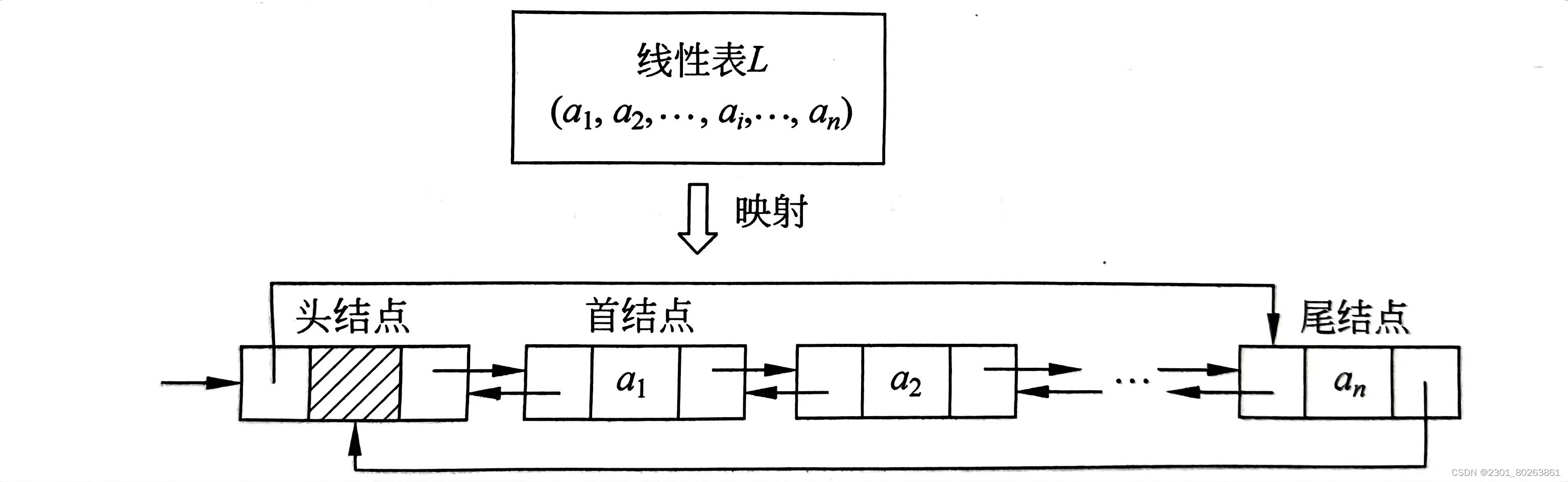
数据结构的概念大合集02(线性表)
概念大合集02 1、线性表及其逻辑结构1.1 线性表的定义1.2 线性表的基本操作 2、线性表的顺序存储结构2.1 顺序表 3、线性表的链式存储3.1 链表3.1.1 头结点(头指针),首指针,尾指针,尾结点3.1.2 单链表3.1.3 双链表3.1.…...
CSS3DRenderer, CSS3DSprite API 使用案例demo
CSS3DRenderer, CSS3DSprite API 使用案例demo <!DOCTYPE html> <html><head><title>three.js css3d - sprites</title><meta charset"utf-8"><meta name"viewport" content"widthdevice-width, user-scalabl…...
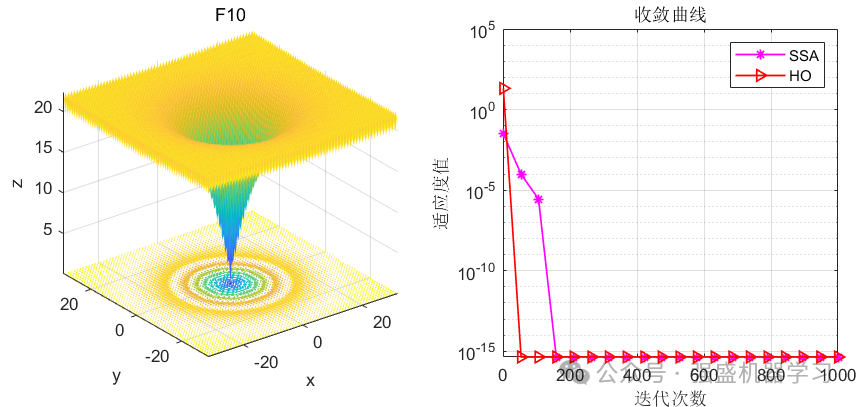
河马优化算法(HO)-2024年Nature子刊新算法 公式原理详解与性能测评 Matlab代码免费获取
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~ 目录 原理简介 一、种群初始化 二、河马在河流或…...
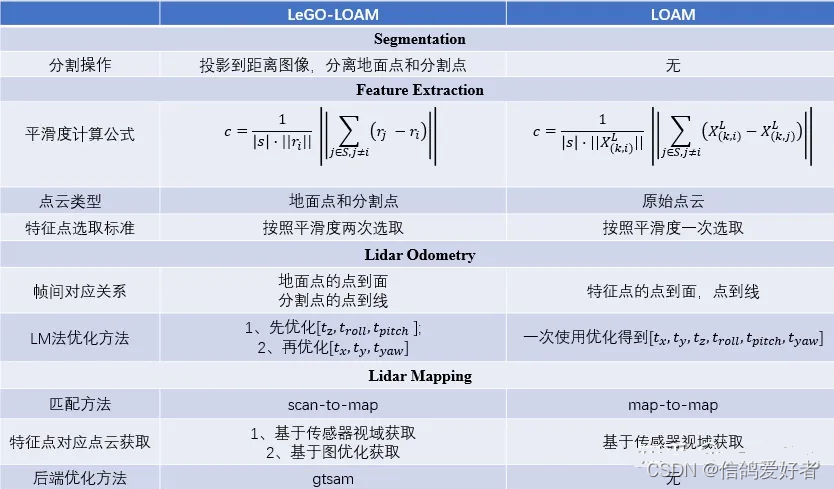
SLAM 算法综述
LiDAR SLAM 其主要思想是通过两个算法:一个高频激光里程计进行低精度的运动估计,即使用激光雷达做里程计计算两次扫描之间的位姿变换;另一个是执行低频但是高精度的建图与校正里程计,利用多次扫描的结果构建地图,细化位…...

搭建Hadoop3.x完全分布式集群
零、资源准备 虚拟机相关: VMware workstation 16:虚拟机 > vmware_177981.zipCentOS Stream 9:虚拟机 > CentOS-Stream-9-latest-x86_64-dvd1.iso Hadoop相关 jdk1.8:JDK > jdk-8u261-linux-x64.tar.gzHadoop 3.3.6&am…...
)
linux常用命令(二)
目录 前言 常用命令 1.ls命令 2. cd命令 3.pwd命令 4.mkdir 命令 5. rmdir 命令 6.rm 命令 7.cp命令 8.mv命令 9.touch命令 10.cat命令 11.more命令 12.less命令 13.head命令 14.tail命令 15.tail命令 16.find命令 17.tar命令 18.gzip命令 19.gunzip命令 …...

【Vue】Request模块 - axios 封装Vuex的持久化存储
📝个人主页:五敷有你 🔥系列专栏:Vue ⛺️稳中求进,晒太阳 Request模块 - axios 封装 使用axios来请求后端接口,一般会对axios进行一些配置(比如配置基础地址,请求响应拦截器…...

【2024第一期CANN训练营】4、AscendCL推理应用开发
文章目录 【2024第一期CANN训练营】4、AscendCL推理应用开发1. 创建代码目录2. 构建模型2.1 下载原始模型文件2.2 使用ATC工具转换模型2.3 注意事项 3. 模型加载3.1 示例代码 4. 模型执行4.1 获取模型描述信息4.2 准备输入/输出数据结构4.3 执行模型推理4.4 释放内存和数据类型…...
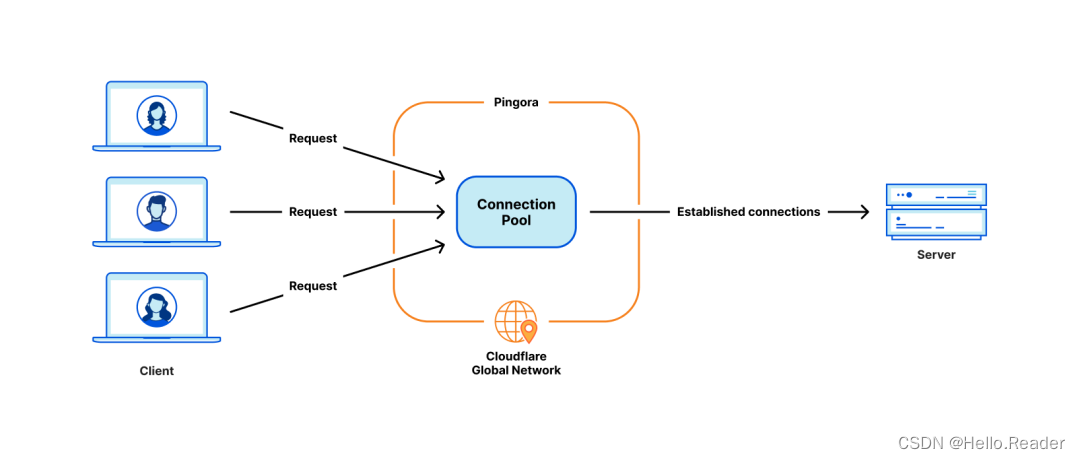
Rust 构建开源 Pingora 框架可以与nginx媲美
一、概述 Cloudflare 为何弃用 Nginx,选择使用 Rust 重新构建新的代理 Pingora 框架。Cloudflare 成立于2010年,是一家领先的云服务提供商,专注于内容分发网络(CDN)和分布式域名解析。它提供一系列安全和性能优化服务…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
