【LeetCode】动态规划--题目练习
有关动态规划算法的整理:添加链接描述
1.爬楼梯
- 爬楼梯:LeetCode70
int climbStairs(int n) {//1.确定dp数组和意义 dp[n]表示第n阶的方法//2.确定递推关系式 dp[n] = dp[n-1]+dp[n-2];//3.初始化int dp[50] = {0};dp[1] = 1;dp[2] = 2;for(int i = 3;i<=n;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];
}
2.第 N 个泰波那契数
1137.第 N 个泰波那契数:LeetCode1137
int tribonacci(int n){//1.确定dp数组和意义 dp[n]表示第n个数//2.确定递推关系式 dp[n] = dp[n-1]+dp[n-2]+dp[n-3];//3.初始化int dp[100] = {0};dp[0] = 0;dp[1] = 1;dp[2] = 1;for(int i = 3;i<=n;i++){dp[i] = dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
3.使用最小花费爬楼梯
746.使用最小花费爬楼梯:LeetCode746
int minCostClimbingStairs(int* cost, int costSize) {//1.确定dp数组和意义 dp[n]表示第n台阶最小花费//2.确定递推关系式 dp[n] = min(dp[n-1]+cost[n-1],dp[n-2]+cost[n-2]);//3.初始化 dp[0] = 0;dp[1] = 0int dp[costSize + 1];dp[0] = dp[1] = 0;for (int i = 2; i <= costSize; i++) {dp[i] = fmin(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[costSize];
}
4.打家劫舍
198.打家劫舍:LeetCode198
int rob(int* nums, int numsSize) {//1.确定dp数组和意义 dp[n]表示最大金额//2.确定递推关系式 dp[n] = max()//3.初始化 dp[0];dp[1] //考虑特殊情况int dp[numsSize+1];dp[0] = nums[0];if(numsSize == 1){return nums[0];}//只有两家if(nums[1]<nums[0]){dp[1] = dp[0];}else{dp[1] = nums[1];}//dp[1] = nums[1];for(int i = 2;i<numsSize;i++){dp[i]=fmax(dp[i-2]+nums[i],dp[i-1]);}//dp[numsSize-1]=fmax(dp[numsSize-3]+nums[numsSize-1],dp[numsSize-2]);return dp[numsSize-1];}
5.最小路径和
64.最小路径和:[LeetCode64]
int minPathSum(int** grid, int gridSize, int* gridColSize) {//向下 (i,j+1)向右(i+1,j)//1.确定dp数组和意义 dp[m-1][n-1]是最小的数字和//2.确定递推关系式 dp[m-1][n-1] = fmin(dp[m-1-1][n-1],dp[m-1][n-1-1])+grid[m-1][n-1];//向上寻找,向左寻找//3.初始化 dp[0][0] = grid[0][0];//考虑特殊情况int rows = gridSize, columns = gridColSize[0];if (rows == 0 || columns == 0) {return 0;}int dp[rows][columns];dp[0][0] = grid[0][0];for (int i = 1; i < rows; i++) {dp[i][0] = dp[i - 1][0] + grid[i][0];}for (int j = 1; j < columns; j++) {dp[0][j] = dp[0][j - 1] + grid[0][j];}for (int i = 1; i < rows; i++) {for (int j = 1; j < columns; j++) {dp[i][j] = fmin(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[rows - 1][columns - 1];
}6.不同路径
62.不同路径:[LeetCode62]
int uniquePaths(int m, int n) {//向下 (i,j+1)向右(i+1,j)//1.确定dp数组和意义 dp[m-1][n-1]是最多的路径//2.确定递推关系式 dp[m-1][n-1] = dp[m-1-1][n-1]+dp[m-1][n-1-1];//向上寻找,向左寻找//3.初始化 dp[0][0] = 0//考虑特殊情况 只有一行 一列int dp[m][n];dp[0][0] = 0;if(m==1||n==1){return 1;}for(int i = 0;i<m;i++){dp[i][0] = 1;}for(int j = 0;j<n;j++){dp[0][j] = 1;}dp[0][1]=1;dp[1][0]=1;for(int i = 1;i<m;i++){for(int j = 1;j<n;j++){dp[i][j] = dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];
}
7.下降路径最小和
931.下降路径最小和:LeetCode931
int minFallingPathSum(int** matrix, int matrixSize, int* matrixColSize) {int n=matrixSize;//n*n//int n=matrixColSize[0];//列数//三个位置 [i+1][j+1];[i+1][j];[i+1][j-1]//1.确定dp数组和意义 dp[][]最后比较大小//2.确定递推关系式 dp[i][j] = fmin(fmin(dp[i-1][j],dp[i-1][j-1]),dp[i-1][j+1])+ma[i][j];//3.初始化 第一行 dp = ma[][];//考虑特殊情况int dp[110][110]={{0}};//初始化for(int i = 0;i<n;i++){dp[0][i]=matrix[0][i];}if(n==1){return matrix[0][0];}if(n==2){dp[1][1]=fmin(dp[0][1],dp[0][0])+matrix[1][1];dp[1][0]=fmin(dp[0][1],dp[0][0])+matrix[1][0];return fmin(dp[1][1],dp[1][0]);}for(int i = 1;i<n;i++){for(int j=0;j<n;j++){if(j+1>=n){//右边界列dp[i][n-1]=fmin(dp[i-1][n-1],dp[i-1][n-2])+matrix[i][n-1];}else if(j-1<0){//左边界列dp[i][0]=fmin(dp[i-1][0],dp[i-1][1])+matrix[i][0];}else{dp[i][j]=fmin(fmin(dp[i-1][j],dp[i-1][j-1]),dp[i-1][j+1])+matrix[i][j];} }}int mm=99999;//求最后一行最小值for(int i = 1;i<n;i++){mm = fmin(fmin(dp[n - 1][i - 1], dp[n - 1][i]),mm);}return mm;
}
相关文章:

【LeetCode】动态规划--题目练习
有关动态规划算法的整理:添加链接描述 1.爬楼梯 爬楼梯:LeetCode70 int climbStairs(int n) {//1.确定dp数组和意义 dp[n]表示第n阶的方法//2.确定递推关系式 dp[n] dp[n-1]dp[n-2];//3.初始化int dp[50] {0};dp[1] 1;dp[2] 2;for(int i 3;i<n;i){dp[i] …...

【LeetCode热题100】101. 对称二叉树(二叉树)
一.题目要求 给你一个二叉树的根节点 root , 检查它是否轴对称。 二.题目难度 简单 三.输入样例 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true 示例 2: 输入:root [1,2,2,null,3,null,3] 输出&a…...

VLC抓取m3u8视频
前言 最近想看一些网络视频,但是很多时候网页上是m3u8推流的,如果在线看,速度又慢,所以就想下载下来,就想到了VLC的推流,转换能力,查阅资料,加上实践,总结心得。 设置中…...

聊聊Python都能做些什么
文章目录 一、Python简介二、Python都能做些什么1. Web开发2. 数据分析和人工智能3. 自动化运维和测试4. 网络爬虫5. 金融科技 三、Python开源库都有哪些1. Web开发2. 数据分析和科学计算3. 机器学习和深度学习4. 网络爬虫5. 自动化和测试6. 其他常用库 四、相关链接 一、Pytho…...

JavaWeb06-MVC和三层架构
目录 一、MVC模式 1.概述 2.好处 二、三层架构 1.概述 三、MVC与三层架构 四、练习 一、MVC模式 1.概述 MVC是一种分层开发的模式,其中 M:Model,业务模型,处理业务 V: View,视图,界面展…...

MySQL数据库实现增删改查基础操作
准备工作 安装mysql8.0 (安装时一定要记住用户名和密码)安装数据库可视化视图工具Navicat 请注意⚠️⚠️⚠️⚠️ a. 编程类所有软件不要安装在中文目录下 b. Navicat破解版下载安装教程:(由于文章审核提示版权问题,链接不方便给出ÿ…...
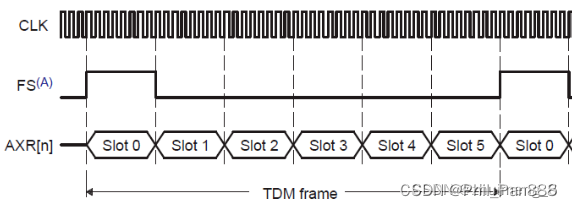
PCM和I2S区别
I2S和PCM接口都是数字音频接口,而所见的蓝牙到cpu以及codec的音频接口都是用PCM接口,是不是两个接口有各自不同的应用呢?先来看下概念。 PCM(PCM-clock、PCM-sync、PCM-in、PCM-out)脉冲编码调制,模拟语音信…...
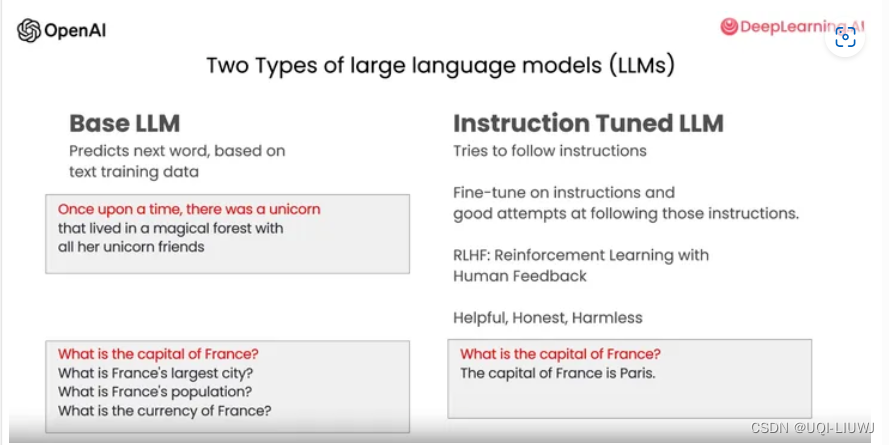
大模型笔记:吴恩达 ChatGPT Prompt Engineering for Developers(1) prompt的基本原则和策略
1 intro 基础大模型 VS 用指令tune 过的大模型 基础大模型 只会对prompt的文本进行续写 所以当你向模型发问的时候,它往往会像复读机一样续写几个问题这是因为在它见过的语料库文本(通常大多来自互联网)中,通常会连续列举出N个问…...

设计模式 — — 单例模式
一、是什么 单例模式只会在全局作用域下创建一次实例对象,让所有需要调用的地方都共享这一单例对象 二、实现 // 单例构造函数 function CreateSingleton (name) {this.name name;this.getName(); };// 获取实例的名字 CreateSingleton.prototype.getName func…...
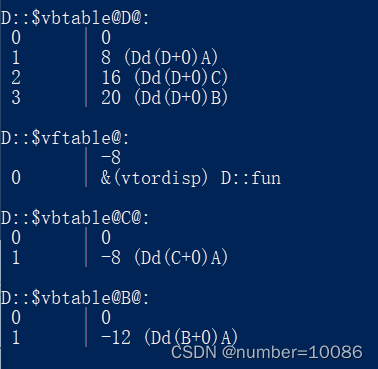
C++:菱形继承与虚继承
看下面这个示例代码 class A{ public: int num10; A(){cout<<"A构造"<<endl;} virtual void fun(){cout<<"A虚函数"<<endl;} };class B:public A{ public: B(){cout<<"B构造"<<endl;} void fun(){cout<…...

贡献法:USACO 2021 December Contest Bronze:孤独的照片
Farmer John 最近购入了 N 头新的奶牛,每头奶牛的品种是更赛牛(Guernsey)或荷斯坦牛(Holstein)之一。 奶牛目前排成一排,Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。 然而,他…...

Java实现简单的通讯录
每日一言 泪眼问花花不语,乱红飞过秋千去。 —欧阳修- 简单的通讯录实现,跟写Java实现图书管理系统差不多,用到的知识也差不多,就当个小练习,练习一下写Java程序的手感。 Java实现图书管理系统 关于通讯录的代码都写…...

服务器数据恢复—raid5热备盘上线同步数据失败的如何恢复数据
服务器数据恢复环境&故障&分析: 一台存储上有一组由多块硬盘组建的raid5阵列,该raid5阵列中的一块硬盘掉线,热备盘自动上线同步数据的过程中,raid阵列中又有一块硬盘掉线,热备盘的数据同步被中断,r…...
探索C语言中的循环结构
循环结构是程序设计中一种重要的控制结构,它允许程序重复执行特定的代码块,直到满足某个条件为止。在C语言中,循环结构有多种形式,如for循环、while循环和do-while循环。本文将介绍C语言中的循环结构,并讨论它们的用法…...

数学建模-估计出租车的总数
文章目录 1、随机抽取的号码在总体的排序 1、随机抽取的号码在总体的排序 10个号码从小到大重新排列 [ x 0 , x ] [x_0, x] [x0,x] 区间内全部整数值 ~ 总体 x 1 , x 2 , … , x 10 总体的一个样本 x_1, x_2, … , x_{10} ~ 总体的一个样本 x1,x2,…,x10 总体的一个样…...

设计模式在芯片验证中的应用——装饰器
一、装饰器模式 装饰器模式(Decorator)是一种结构化软件设计模式,它提供了一种通过向类对象添加行为来修改类对象的方法,而不会影响同一类的其它对象行为。该模式允许在不修改抽象类的情况下添加类功能。它从本质上允许基类代码对不可预见的修改具有前瞻…...

Python 查找并高亮PDF中的指定文本
在处理大量PDF文档时,有时我们需要快速找到特定的文本信息。本文将提供以下三个Python示例来帮助你在PDF文件中快速查找并高亮指定的文本。 查找并高亮PDF中所有的指定文本查找并高亮PDF某个区域内的指定文本使用正则表达式搜索指定文本并高亮 本文将用到国产第三方…...

LEETCODE LCS 03. 主题空间
题目描述如上,这个题主要运用了DFS的思想,同时走过的路径标记为6,即可在后续的遍历中过滤掉重复的元素,其他则类似边界条件的判断和题目条件的判断,求最大值,只需要一次遍历中累加对比每一次得即可。 模板&…...
【Spring Boot 源码学习】深入应用上下文初始化器实现
《Spring Boot 源码学习系列》 深入应用上下文初始化器实现 一、引言二、往期内容三、主要内容3.1 spring-boot 子模块中内置的实现类3.1.1 ConfigurationWarningsApplicationContextInitializer3.1.2 ContextIdApplicationContextInitializer3.1.3 DelegatingApplicationConte…...
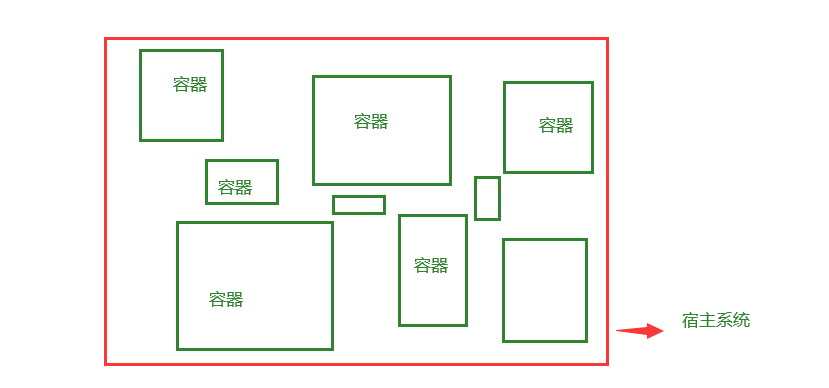
【Docker】一文趣谈Docker
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》《项目实战》 🛸学无止境,不骄不躁,知行合一 文章目录 …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
