C#八皇后算法:回溯法 vs 列优先法 vs 行优先法 vs 对角线优先法
目录
1.八皇后算法(Eight Queens Puzzle)
2.常见的八皇后算法解决方案
(1)列优先法(Column-First Method):
(2)行优先法(Row-First Method):
(3)对角线优先法(Diagonal-First Method):
(4)回溯法(Backtracking):
1.八皇后算法(Eight Queens Puzzle)
皇后问题是一个古老而著名的问题,它实质上就是使棋盘上的8个皇后不能在同一行、同一列或同一条斜线上,共有92种方案。
2.常见的八皇后算法解决方案
八皇后算法的解决方案有多种,以下是一些常见的解决方案:
(1)列优先法(Column-First Method):
八皇后问题是一个经典的回溯算法问题,可以使用列优先法(或称为逐列解决法)来解决。 首先选择一个空的棋盘,然后从第一行开始,尝试将皇后放置在每一列。如果当前列没有被攻击,那么就将皇后放置在该列。否则,尝试下一列。当找到一个有效的列时,将皇后放置在该列的最下方。重复这个过程,直到所有的皇后都被放置在棋盘上。
// 使用列优先法解决八皇后问题
// 列优先算法也叫逐列解决法namespace _144_4
{class Program{private const int Size = 8;private readonly int[] queens = new int[Size]; // 存储每行皇后的列位置private readonly bool[] columns = new bool[Size]; // 列是否已被占用private readonly bool[] diagonals1 = new bool[2 * Size - 1]; // 主对角线是否已被占用private readonly bool[] diagonals2 = new bool[2 * Size - 1]; // 副对角线是否已被占用public void Solve(){PlaceQueen(0);}int solnum = 0;private void PlaceQueen(int row){if (row == Size){solnum += 1;PrintQueens(solnum); // 所有皇后都已放置,打印结果return;}for (int col = 0; col < Size; col++){if (IsSafe(row, col)){queens[row] = col;columns[col] = true;diagonals1[row - col + Size - 1] = true;diagonals2[row + col] = true;PlaceQueen(row + 1);// 回溯diagonals2[row + col] = false;diagonals1[row - col + Size - 1] = false;columns[col] = false;}}}private bool IsSafe(int row, int col){return !columns[col] && !diagonals1[row - col + Size - 1] && !diagonals2[row + col];}private void PrintQueens(int solnum){Console.WriteLine("Solution{0}: ", solnum);for (int i = 0; i < Size; i++){for (int j = 0; j < Size; j++){if (queens[i] == j){Console.Write("Q ");}else{Console.Write("* ");}}Console.WriteLine();}Console.WriteLine();}public static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);Program solver = new();solver.Solve();}}
}- 算法流程
初始化所有数组。
从第一行开始,尝试在每一列放置皇后。
使用回溯法,如果在某一行找不到安全的位置,则返回到上一行并尝试下一个位置。
当所有皇后都成功放置时,打印解决方案。
- 方法分析
Solve():启动算法,从第一行开始放置皇后。
PlaceQueen(int row):递归方法,尝试在当前行的每一列放置皇后。如果找到一个安全的位置,则递归地尝试放置下一个皇后。如果所有皇后都已成功放置,则打印解决方案。
IsSafe(int row, int col):检查在给定位置 (row, col) 放置皇后是否安全。如果列、主对角线和副对角线都没有被占用,则返回 true。
PrintQueens(int solnum):打印解决方案。对于每一行,如果当前列有皇后,则打印 "Q",否则打印 "*"。
(2)行优先法(Row-First Method):
与列优先法类似,但不同之处在于,该方法从第一列开始,尝试将皇后放置在每一行。如果当前行没有被攻击,那么就将皇后放置在该行的最右侧。否则,尝试下一行。当找到一个有效的行时,将皇后放置在该行的当前列。重复这个过程,直到所有的皇后都被放置在棋盘上。
// 使用行优先法解决八皇后问题
// 行优先算法也叫回溯法
namespace _144_3
{class Program{static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);List<int[]> solutions = [];int[] solution = new int[8];Solve(0, solution, solutions);foreach (int[] sol in solutions){for (int i = 0; i < 8; i++){for (int j = 0; j < 8; j++){if (j == sol[i]){Console.Write("Q ");}else{Console.Write(". ");}}Console.WriteLine();}Console.WriteLine();}}static void Solve(int row, int[] solution, List<int[]> solutions){if (row == solution.Length){//solutions.Add(solution.ToArray()); // Add a copy of the solutionsolutions.Add([.. solution]);return;}for (int col = 0; col < solution.Length; col++){if (IsSafe(row, col, solution)){solution[row] = col;Solve(row + 1, solution, solutions);}}}static bool IsSafe(int row, int col, int[] solution){for (int i = 0; i < row; i++){if (solution[i] == col ||Math.Abs(solution[i] - col) == Math.Abs(i - row)){return false;}}return true;}}
}代码使用了行优先法(也称为回溯法)来解决八皇后问题,这是一个经典的递归回溯问题。 代码分析:
- Main 方法
Main 方法是程序的入口点。
它首先检查 args 是否为空,如果为空则抛出异常。
初始化一个空列表 solutions 来存储所有解决方案。
调用 Solve 方法来寻找解决方案。
遍历 solutions 列表,并打印出每一个解决方案。
- Solve 方法
Solve 方法是递归函数,用于寻找八皇后问题的解决方案。
如果当前行 row 等于解决方案数组的长度(即8),则找到一个解决方案,并将其添加到 solutions 列表中。
对于当前行的每一列,检查是否安全(没有冲突),如果安全则在该列放置皇后,并递归调用 Solve 方法处理下一行。
- IsSafe 方法
IsSafe 方法用于检查在当前位置 (row, col) 放置皇后是否安全。
它遍历已经放置皇后的行,检查当前列和左上方对角线是否有冲突。
如果没有冲突,返回 true;否则返回 false。
- 注意事项
在 Main 方法中,使用了 ArgumentNullException.ThrowIfNull(args); 来检查 args 是否为空。这通常用于命令行应用程序,但在没有实际命令行参数需求的程序中是不必要的。
在 Solve 方法中,使用了 solutions.Add([.. solution]); 来添加解决方案的副本到 solutions 列表。这是C# 9.0引入的切片语法,用于创建数组或列表的浅拷贝。用这个简洁的方式来避免直接添加引用到同一个数组。
(3)对角线优先法(Diagonal-First Method):
该方法首先选择一个空的棋盘,然后从左上角开始,尝试将皇后放置在对角线上。如果当前对角线没有被攻击,那么就将皇后放置在该对角线的最下方。否则,尝试下一个对角线。当找到一个有效的对角线时,将皇后放置在该对角线的当前列。重复这个过程,直到所有的皇后都被放置在棋盘上。
// 八皇后算法_对角线优先法
namespace _144_2
{class Program{static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);int n = 8;int[] queens = new int[n];List<int[]> solutions = [];SolveQueens(n, queens, 0, solutions);Console.WriteLine("Total solutions: " + solutions.Count);foreach (int[] solution in solutions){for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (j == solution[i]){Console.Write("Q ");}else{Console.Write(". ");}}Console.WriteLine();}Console.WriteLine();}}static void SolveQueens(int n, int[] queens, int index, List<int[]> solutions){if (index == n){solutions.Add([.. queens]);return;}for (int i = 0; i < n; i++){if (CanPlaceQueen(queens, index, i)){queens[index] = i;SolveQueens(n, queens, index + 1, solutions);}}}static bool CanPlaceQueen(int[] queens, int index, int col){for (int i = 0; i < index; i++){if (queens[i] == col || Math.Abs(queens[i] - col) == index - i){return false;}}return true;}}
}在这个示例中,使用一个整数数组queens来表示棋盘上皇后的位置。queens数组的每个元素表示对应行上皇后的列位置。
使用递归函数SolveQueens来解决八皇后问题。该函数接受当前皇后的位置、当前行号和已找到的解作为参数。在递归过程中,尝试在每一列上放置皇后,并检查是否满足问题的约束条件。如果满足,则将皇后放置在当前行的对应列上,并继续递归处理下一行。如果当前行的所有列都满足约束条件,则表示找到一个解,并将解添加到已找到的解列表中。
函数CanPlaceQueen用于检查在给定位置放置皇后是否满足约束条件。它接受棋盘大小、当前皇后的位置、当前行号和当前列号作为参数。在函数中,遍历当前行号之前的行,检查当前列号是否已经放置了皇后,或者当前行和列上的皇后是否在同一条对角线上。如果满足任一条件,则表示不能在当前位置放置皇后。
在Main函数中,输出找到的解决方案。对于每个解决方案,遍历8行8列,如果当前列是皇后的位置,则输出"Q",否则输出"."。
(4)回溯法(Backtracking):
该方法通过递归的方式尝试所有可能的皇后位置。算法步骤如下:
- 选择一个空的棋盘。
- 选择一个皇后,将其放置在棋盘的第一行的任意一列。
- 选择下一个皇后,将其放置在下一行的任意一列,但不能与第一个皇后位于同一列或同一对角线上。
- 重复步骤3,直到所有的皇后都被放置在棋盘上。
// 八皇后算法_回溯法
namespace _144
{class Program{#region 八皇后算法/// <summary>/// 解决八皇后问题/// </summary>/// <param name="size">皇后数量</param>static void QueenArithmetic(int size){int[] Queen = new int[size];//每行皇后的位置int y, x, i, j, d, t = 0;y = 0;Queen[0] = -1;while (true){for (x = Queen[y] + 1; x < size; x++){for (i = 0; i < y; i++){j = Queen[i];d = y - i;//检查新皇后是否能与以前的皇后相互攻击if ((j == x) || (j == x - d) || (j == x + d))break;}if (i >= y)break; //不攻击}if (x == size) //没有合适的位置{if (0 == y){Console.WriteLine("Over"); //回溯到了第一行break; //结束}Queen[y] = -1; //回溯y--;}else{Queen[y] = x; //确定皇后的位置y++; //下一个皇后if (y < size)Queen[y] = -1;else{Console.WriteLine("\n" + ++t + ':');//所有的皇后都排完了,输出for (i = 0; i < size; i++){for (j = 0; j < size; j++)Console.Write(Queen[i] == j ? 'Q' : '*');Console.WriteLine();}y = size - 1;//回溯}}}Console.ReadLine();}#endregionstatic void Main(string[] args){ArgumentNullException.ThrowIfNull(args);int size = 8; //皇后数QueenArithmetic(size);}}
}相关文章:

C#八皇后算法:回溯法 vs 列优先法 vs 行优先法 vs 对角线优先法
目录 1.八皇后算法(Eight Queens Puzzle) 2.常见的八皇后算法解决方案 (1)列优先法(Column-First Method): (2)行优先法(Row-First Method)&a…...

springboot整合swagger,postman,接口规范
一、postman介绍 1.1概述 工具下载 Postman(发送 http 请求的工具) 官网(下载速度比较慢):Download Postman | Get Started for Free 网盘下载:百度网盘 请输入提取码 1.2Http 请求格式 请求地址请求方法状…...

029—pandas 遍历行非向量化修改数据
前言 在 pandas 中,向量化计算是指利用 pandas 对象的内置方法和函数,将操作应用到整个数据结构的每个元素,从而在单个操作中完成大量的计算。 但在一些需求中,我们无法使用向量化计算,就需要迭代操作,本例…...

相机安装位置固定后开始调试设备供电公司推荐使用方法
摄像头安装位置固定后开始调试 设备供电:无电源设备需要连接12V/2A电源并连接到摄像机的DC端口,而有电源的摄像机可以直接连接到220V电源。 连接设备:如果是有线连接,请使用网线将设备连接到电脑(建议直接连接&#…...

AI视频批量混剪系统|罐头鱼AI视频矩阵获客
AI视频批量混剪系统助您轻松管理和编辑视频素材 如今,视频营销已成为企业推广的重要方式。为了满足用户对视频管理、发布和编辑的需求,《罐头鱼AI视频批量混剪系统》应运而生。这款智能化系统集成了多种功能,助您轻松管理和发布精彩视频内容…...

线程池学习-了解,自定义线程池
什么是线程池,这个池字是什么 线程池,主要利用池化思想,线程池,字符串常量池等 为什么要有一个线程池? 正常线程的创建:1,手动创建一个线程 2.给该线程分配任务,线程执行任务 3…...

CentOS7.9 安装SIPp3.6
epel里面的SIPp版本比较旧,先不要epel yum remove -y epel-release okay有很多CentOS软件,可以这样安装: 编辑 /etc/yum.repos.d/okay.repo,内容为: [okay] nameExtra OKay Packages for Enterprise Linux - $basearc…...
Java零基础入门-LinkedHashMap集合
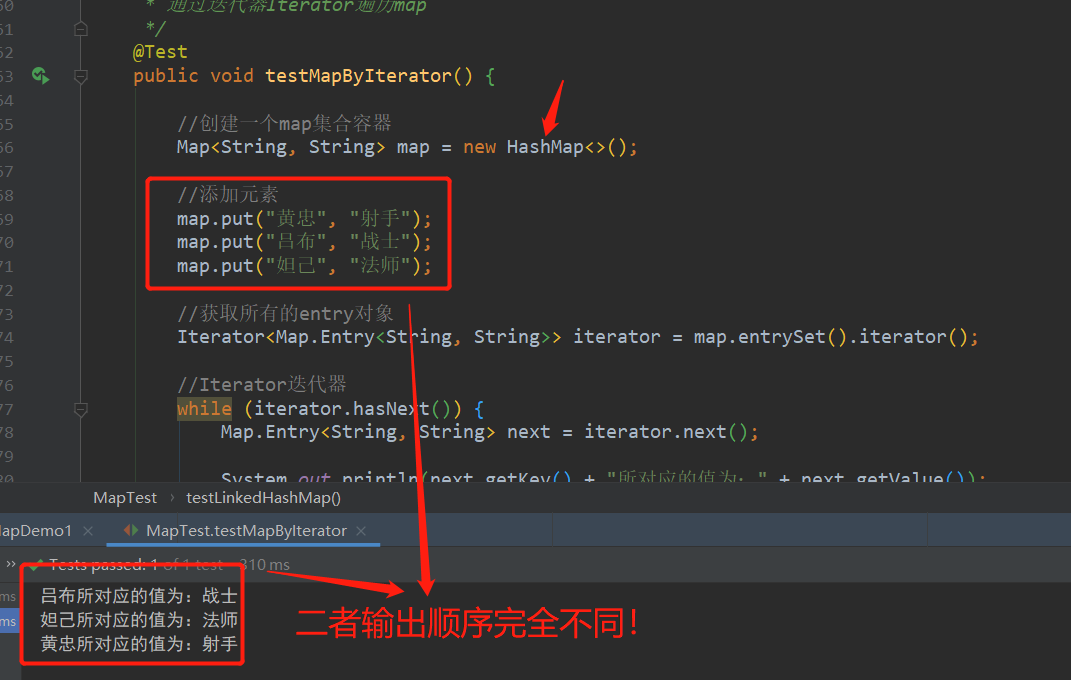
一、本期教学目标 学习LinkedHashMap集合的概念及特点。学习LinkedHashMap存储结构。学习LinkedHashMap集合常用方法及示例代码演示。 二、正文 1、概述 我们学习了map接口之HashMap集合,今天我们要来学习map接口的另一个实现类-LinkedHashMap,不知道…...

LRC转SRT
最近看到一首很好的英文MTV原版,没又字幕,自己找字幕,只找到LRC,ffmpeg不支持LRC,网上在线转了SRT。 Subtitle Converter | Free tool | GoTranscript 然后用 ffmpeg 加字幕 ffmpeg -i LoveMeLikeYouDo.mp4 -vf sub…...

mybatis源码阅读系列(二)
前言 上一篇文章mybatis源码阅读系列(一)介绍了mybatis和原生jdbc的区别,并通过代码展示了两者的运行过程和结果,下面让我们继续详细了解下mybatis的执行过程; package com.wyl.mybatis.service;import com.wyl.mybat…...
【Web开发】CSS教学(超详细,满满的干货)
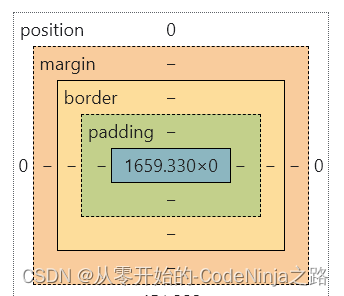
💓 博客主页:从零开始的-CodeNinja之路 ⏩ 收录文章:【Web开发】CSS教学(超详细,满满的干货) 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 CSS一. 什么是CSS?1.1 基本语法规范1.2 引入方式1.3 规范 二. CSS选…...

系列学习前端之第 5 章:学习 ES6 ~ ES11
1、什么是 ECMAScript ECMAScript 是由 Ecma 国际通过 ECMA-262 标准化的脚本程序设计语言。 从第 6 版开始,发生了里程碑的改动,并保持着每年迭代一个版本的习惯。 ES62015年,ES72016年,ES82017年,ES92018年&#…...
Linux学习(4)——使用编辑器
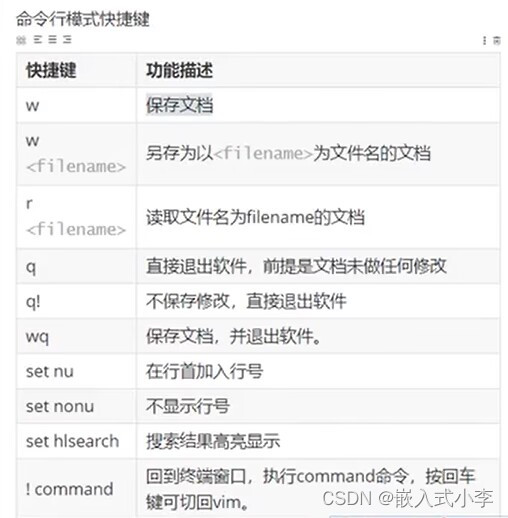
1.gedit编辑器 简单易懂,依赖图形界面。可以使用ctrlc ctrlv等快捷键,ctrls进行保存,与windows系统中相类似。 2.vi/vim编辑器 vi/vim可以直接通过控制台的终端完成文本的编辑,不依赖图形界面,使用范围更广。它的编辑…...

简单函数_短信计费
任务描述 用手机发短信,一条短信资费为0.1元,但限定一条短信的内容在70个字以内(包括70个字)。如果你一次所发送的短信超过了70个字,则会按照每70个字一条短信的限制把它分割成多条短信发送。假设已经知道你当月所发送…...
centos命令history设置记录10000行
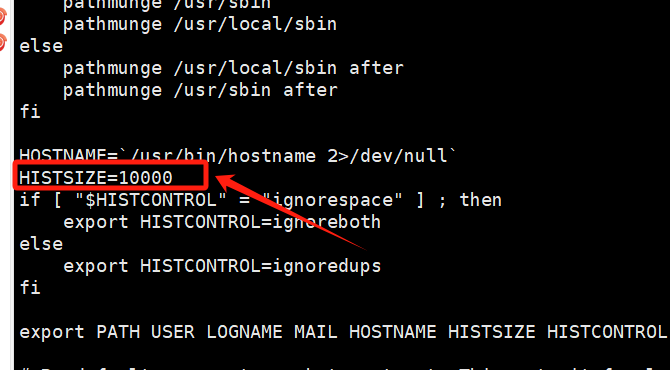
今天在操作服务器的时候,用history查看操作记录的时候,发现只能查看10条,这样不行啊,我想查看所有人对服务器操作的命令。 [rootbogon ~]# history解决办法: #1、找到/etc/profile文件中的histsize 把10改成10000 […...

SpringBoot打造企业级进销存储系统 第七讲
Transientprivate String roles; // 所拥有的角色package com.java1234.entity;import javax.persistence.Column; import javax.persistence.Entity; import javax.persistence.GeneratedValue; import javax.persistence.Id; import javax.persistence.Table; import javax.p…...
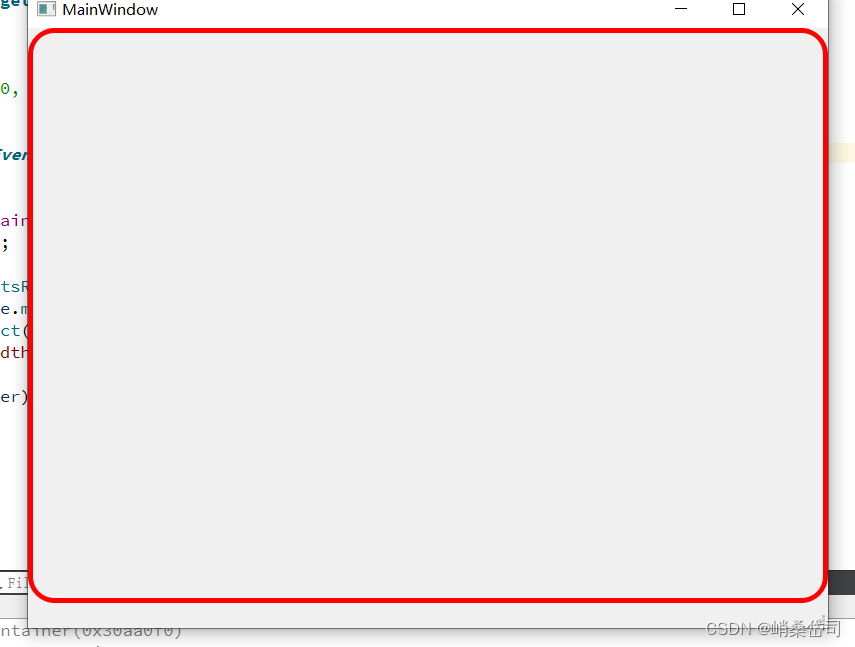
1.实用Qt:解决绘制圆角边框时,圆角锯齿问题
目录 问题描述 解决方案 方案1: 方案2: 结果示意图 问题描述 做UI的时候,我们很多时候需要给绘制一个圆角边框,初识Qt绘制的童鞋,可能绘制出来的圆角边框很是锯齿,而且粗细不均匀,如下图&…...
JavaWeb08-Filter和Listener
目录 一、Filter 1.概述 2.作用 3.快速入门 4.执行流程 5.拦截路径配置 6.拦截器链(多个过滤器) 7.登录验证 二、Listener(了解即可) 1.概述 2.主要作用 3.分类 4.快速入门 一、Filter 1.概述 Filter 表示过滤器&am…...

关于ClickHouse的一些小技巧
关于ClickHouse的一些小技巧 设置变量 set param_nameAlex; select {name:String};projection的使用 基于projection(投影)的优化需要打开开关optimize_use_projections。ClickHouse里的projection是物化的,也就是说数据会复制存一份。 Pr…...
有来团队后台项目-解析7
sass 安装 因为在使用vite 创建项目的时候,已经安装了sass,所以不需要安装。 如果要安装,那么就执行 npm i -D sass 创建文件 src 目录下创建文件 目录结构如图所示: reset.scss *, ::before, ::after {box-sizing: border-…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
