论文阅读_时序模型_iTransformer
1 2 3 4 5 6 7 8 | 英文名称: ITRANSFORMER: INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING 中文名称: ITRANSFORMER:倒置Transformers在时间序列预测中的有效性 链接: https://openreview.net/forum?id=X6ZmOsTYVs 代码: https://github.com/thuml/iTransformer 作者: Yong Liu, Tengge Hu, Haoran Zhang, Haixu Wu, Shiyu Wang, Lintao Ma, Mingsheng Long 机构: 清华大学软件学院, 清华大学国家数字化治理工程技术研究中心, 蚂蚁集团 日期: 2023-10-10 引用次数: 0 |
读后感
作者提出了一个疑问:为什么在很多情况下,时序问题使用 Transformer 结构反而不如线性模型好?按理说,Transformer 作为预测序列化数据的模型,应该更擅长处理时序问题。作者认为可能是数据组织方式不够优化引起。
文章主要讨论了多变量时序预测的问题,即使用多变量的 X 来预测 Y,例如使用过去的天气数据和地域数据等来预测未来的天气。
之前我们处理时序数据也存在相同的问题:每种数据的频率和范围都不一样,如果在某个时间点上对所有数据进行采样也不太合适。
因此,作者提出了针对时间序列的另一种输入方式。以前是将每个时间点的所有变量作为一个 token 传递给模型;而现在,将每个变量的整个时间序列独立地嵌入到一个 token 中。简单来说:如果想要预测明天的天气,就将之前一段时间的天气打包成一个 token 传入模型。这样既可以学习到数据时序的前后关系,也可以学习到不同特征之间的相互作用。

图 -2 基础模型 (上) 与将每个时间步嵌入到时间 token 的 Transformer,iTransformer 将单个变量的整个序列独立嵌入到变量 token 中,这样多变量相关性可以通过注意力机制来描述,序列表示由前馈网络编码。
摘要
目标: 解决 Transformer 模型在预测具有大范围回溯窗口的时间序列时性能下降和计算爆炸的问题。
方法: 提出 iTransformer 的模型,该模型通过重新利用 Transformer 架构的基本组件来解决问题。iTransformer 只对转置的维度应用注意力机制和前馈网络。将与单个变量相关联的一系列时间点嵌入到变量 token 中,这些 token 被注意力机制用于捕捉多变量之间的相关性;同时,对每个变量 token 应用前馈网络以学习非线性表示的时序规律。
结果: iTransformer 模型在具有挑战性的实际数据集上取得了最先进的结果。它提高了不同变量之间的泛化能力,并更好地利用了任意回溯窗口,成为时间序列预测的良好基础骨架。
方法
预测使用前 T 步的 X 来预测将来 S 步的 Y,其中 X,Y 都包含 N 个变量。模型结构如下:

图 4:iTransformer 的整体结构,它与 Transformer 的编码器有着相同的模块结构:(a)不同变量的原始系列独立嵌入到 token 中。(b)自注意力应用于嵌入的变量 token,具有增强的可解释性,揭示了多变量相关性。(c)每个 token 的序列表示由共享前馈网络提取。(d)采用层归一化法来减少变量之间的差异。
简单地说,该模型使用了自我注意力机制来学习变量之间的关系,并且利用前馈神经网络(MLP)来学习时序变化的规律。最后,通过一个简单的投影层(Projection)生成对未来各个变量的预测 Y。
实验
实验包括 6 个真实世界的数据集:ETT、天气、电力、交通、能源等。
主实验多变量预测结果如下:

相关文章:

论文阅读_时序模型_iTransformer
1 2 3 4 5 6 7 8英文名称: ITRANSFORMER: INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING 中文名称: ITRANSFORMER:倒置Transformers在时间序列预测中的有效性 链接: https://openreview.net/forum?idX6ZmOsTYVs 代码: https://github.com/thum…...
Docker 哲学 - 容器操作 -cp
1、拷贝 容器绑定的 volume的 数据,到指定目录 2、匿名挂载 volume 只定义一个数据咋在容器内的path,docker自动生成一个 sha256 的key作为 volume 名字。这个 sha256 跟 commitID 一致都是唯一的所以 ,docker利用这个机制,可以…...

作品展示ETL
1、ETL 作业定义、作业导入、控件拖拽、执行、监控、稽核、告警、报告导出、定时设定 欧洲某国电信系统数据割接作业定义中文页面(作业顶层,可切英文,按F1弹当前页面帮助) 涉及文件拆分、文件到mysql、库到库、数据清洗、数据转…...

python的集合应用
在Python中,集合是一种无序、可变的数据类型,用于存储不重复的元素。Python提供了内置的集合类型 set,以及 frozenset(不可变的集合)。以下是一些Python集合的常见应用场景: 去重: 集合是存储唯…...
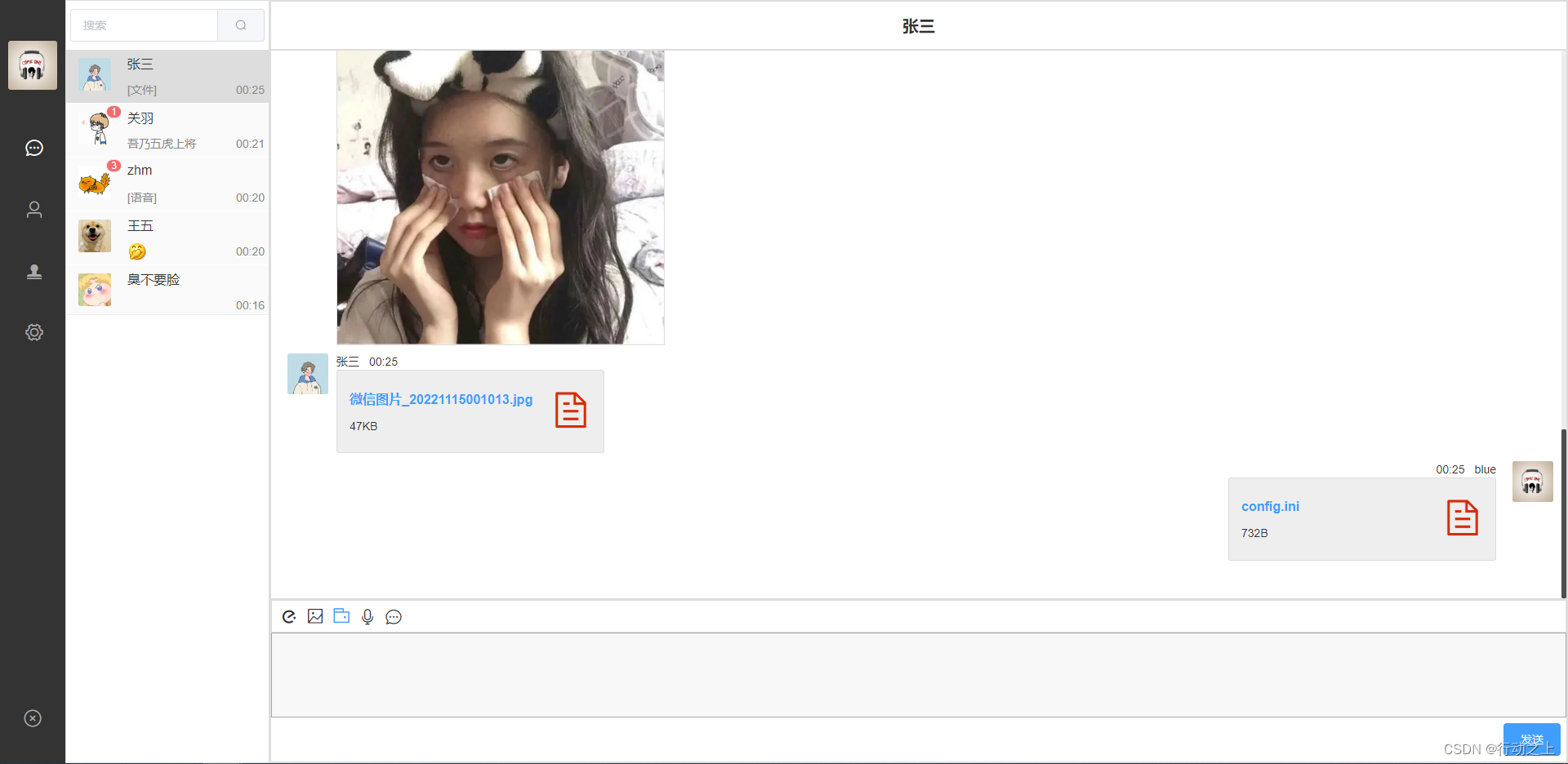
盒子IM开源仿微信聊天程序源码,可以商用
安装教程 1.安装运行环境 安装node:v14.16.0安装jdk:1.8安装maven:3.6.3安装mysql:5.7,密码分别为root/root,运行sql脚本(脚本在im-platfrom的resources/db目录)安装redis:5.0安装minio,命令端口使用9001,并创建一个名为”box-im”的bucket,…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Web)中篇
onBeforeUnload onBeforeUnload(callback: (event?: { url: string; message: string; result: JsResult }) > boolean) 刷新或关闭场景下,在即将离开当前页面时触发此回调。刷新或关闭当前页面应先通过点击等方式获取焦点,才会触发此回调。 参数…...
静默安装OGG21.3微服务版本FOR ORACLE版本
静默安装OGG21.3微服务版本FOR ORACLE版本 silent install ogg21.3 for oracle 某度找来找去都没有找到一份可靠的静默安装OGG21.3微服务版本的案例,特别难受,为此将自己静默安装的步骤一步步贴出来分享给大家,请指点,谢谢。 至…...

[二分查找]LeetCode2040:两个有序数组的第 K 小乘积
本文涉及的基础知识点 二分查找算法合集 题目 给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ,请你返回第 k (从 1 开始编号)小的 nums1[i] * nums2[j] 的乘积,其中 0 < i < nums1.…...

【Godot4.2】颜色完全使用手册
概述 本篇简单汇总Godot中的颜色的构造和使用,内容包括了: RGB、RGBA,HSV以及HTML16进制颜色值、颜色常量等形式构造颜色颜色的运算以及取反、插值用类型化数组、紧缩数组或PNG图片形式存储多个颜色 构造颜色 因为颜色是一种视觉元素&…...
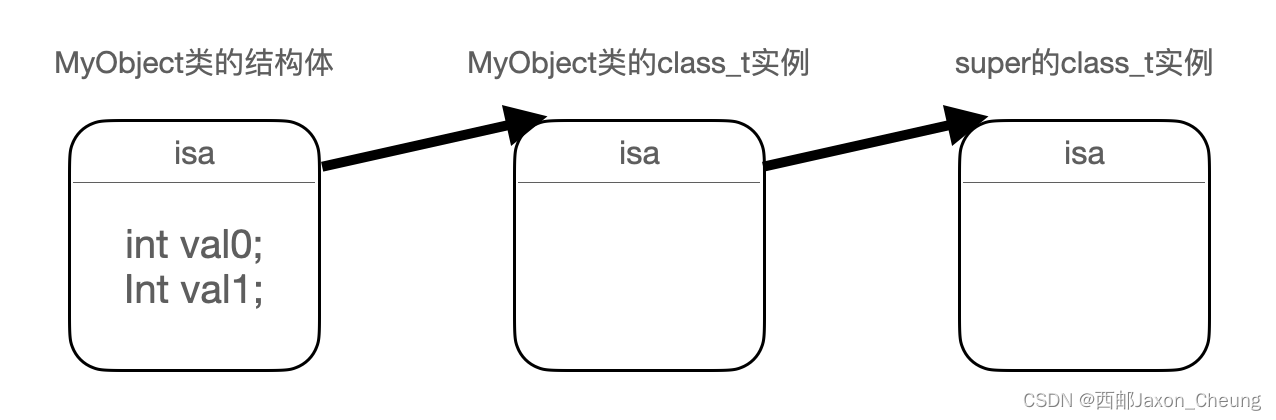
Blocks —— 《Objective-C高级编程 iOS与OS X多线程和内存管理》
目录 Blocks概要什么是BlocksOC转C方法关于几种变量的特点 Blocks模式Block语法Block类型 变量截获局部变量值__block说明符截获的局部变量 Blocks的实现Block的实质 Blocks概要 什么是Blocks Blocks是C语言的扩充功能,即带有局部变量的匿名函数。 顾名思义&#x…...

Python零基础---爬虫技术相关
python 爬虫技术,关于数据相关的拆解: 1.对页面结构的拆解 2.数据包的分析(是否加密了参数)(Md5 aes)难易程度,价格 3.对接客户(433,334) # 数据库 CSV 4.结单(发一部分数据&a…...
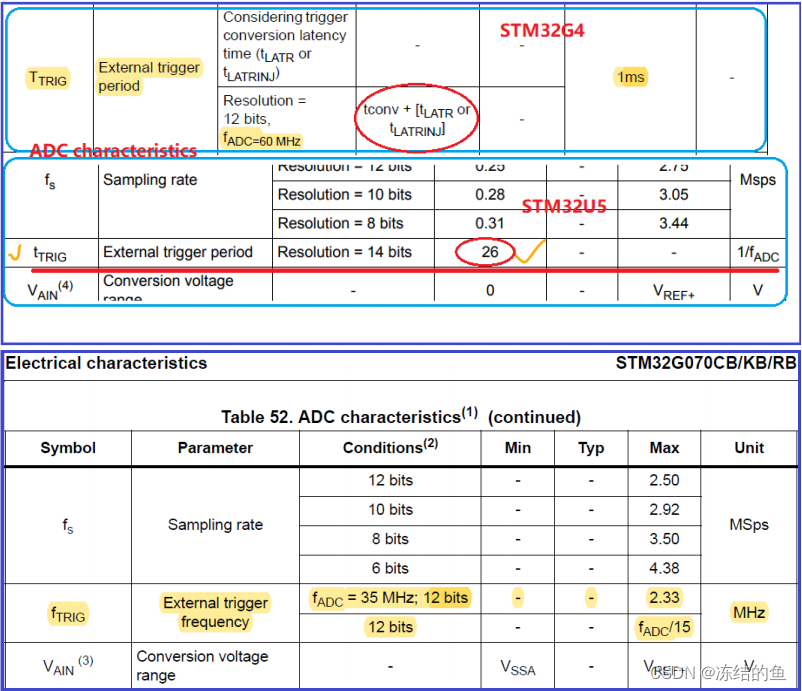
利用 STM32 TIMER 触发 ADC 实现分组转换
1、问题描述 使用 STM32G4 系列芯片开发产品,用到其中一个 ADC 模块的多个通道,他希望使 用 TIMER 来定时触发这几个通道的转换。不过他有两点疑惑。第一,他期望定时器触发这几个 通道是每触发一次则只转换一个通道,这样依次触发…...

2024 年(第 12 届)“泰迪杯”数据挖掘挑战赛——B 题:基于多模态特征融合的图像文本检索完整思路与源代码分享
一、问题背景 随着近年来智能终端设备和多媒体社交网络平台的飞速发展,多媒体数据呈现海量增长 的趋势,使当今主流的社交网络平台充斥着海量的文本、图像等多模态媒体数据,也使得人 们对不同模态数据之间互相检索的需求不断增加。有效的信…...

Java12~14 switch语法
JDK8以后的语法没学习了,现在时代发展这么快,所以得加紧时间学习了。JDK12只有一个特性就是switch语法,算是比较容易学习的一个版本吧。总体来说就是三部分内容。具体内容可以看JEP-325的内容。 箭头语法 每个case可以放箭头了。以下是一个例…...
小狐狸ChatGPT智能聊天系统源码v2.7.6全开源Vue前后端+后端PHP
测试环境包括Linux系统的CentOS 7.6,宝塔面板,PHP 7.4和MySQL 5.6。网站的根目录是public, 使用thinkPHP进行伪静态处理,并已开启SSL证书。 该系统具有多种功能,包括文章改写、广告营销文案创作、编程助手、办公达人…...
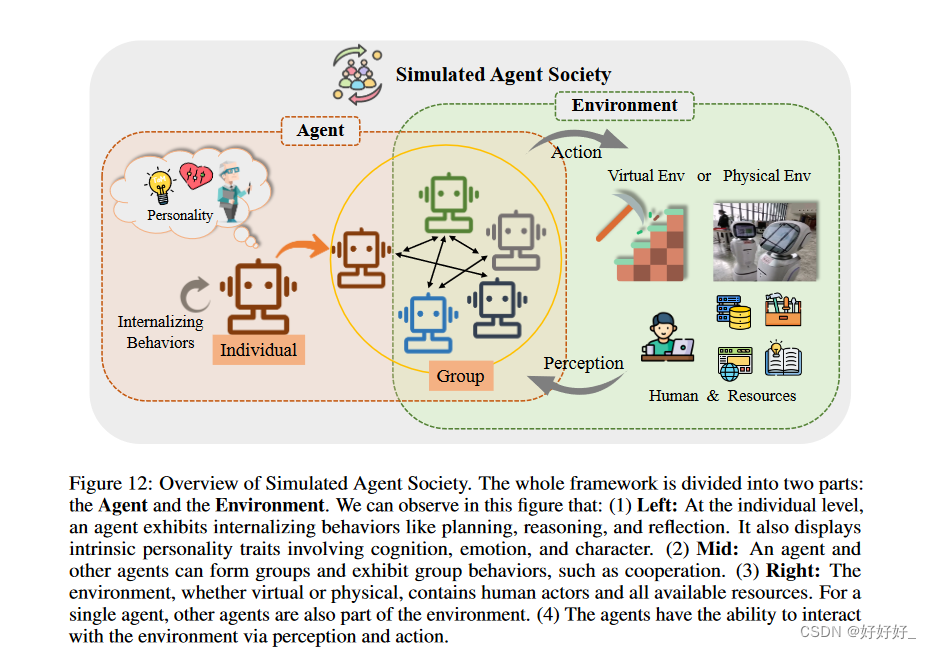
The Rise and Potential of Large Language Model Based Agents: A Survey
OpenAI AI的应用研究主管Lilian Weng发布了关于AI Agents的《大语言模型(LLM)支持的自主代理》,在文章中她定义了基于LLM构建AI Agents的应用框架:AgentLLM(大型语言模型)记忆(Memory࿰…...
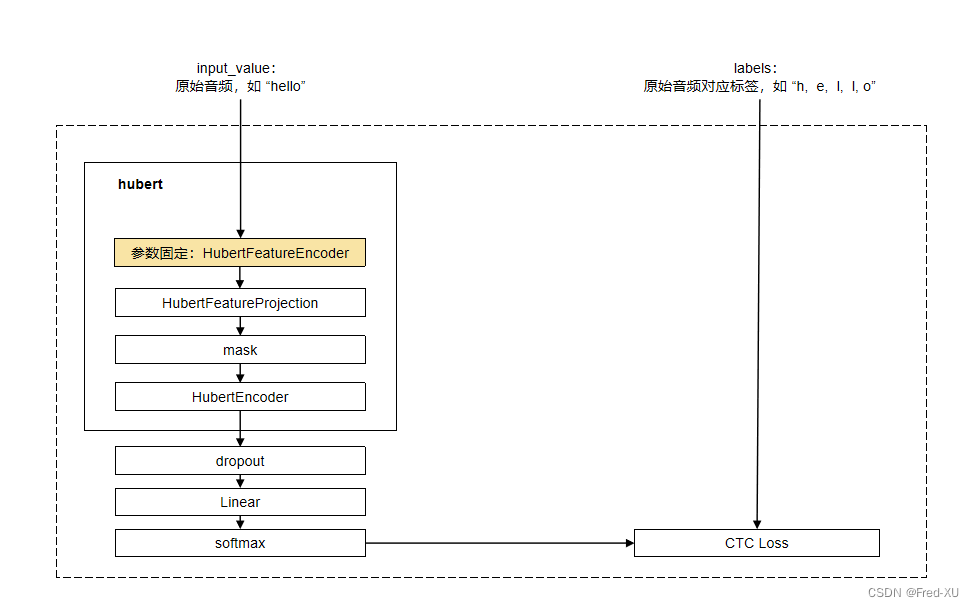
【GPT-SOVITS-06】特征工程-HuBert原理
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...
ros小问题之差速轮式机器人轮子不显示(rviz gazebo)
在rviz及gazebo练习差速轮式机器人时,很奇怪,只有个机器人的底板及底部的两个万向轮,如下图, 后来查看相关.xacro文件,里面是引用包含了轮子的xacro文件,只需传入不同的参数即可调用生成不同位置的轮子&…...
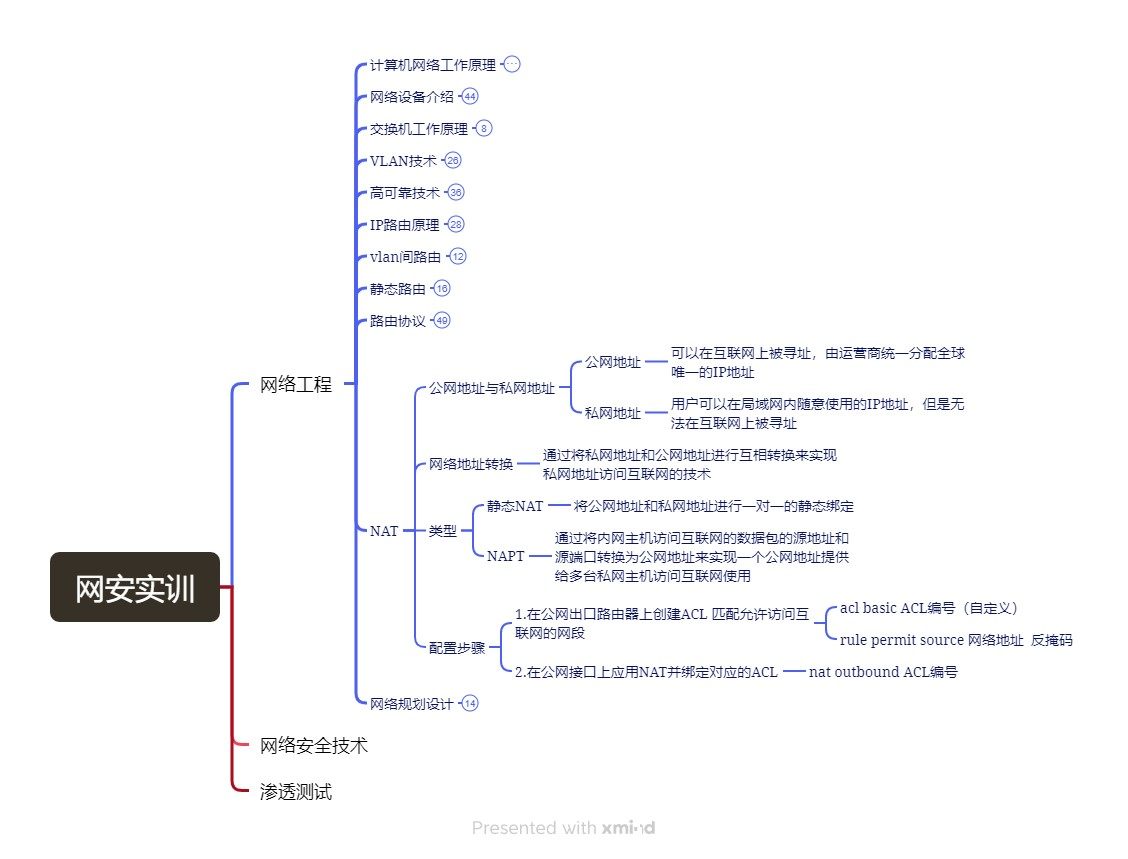
网络安全实训Day5
写在前面 昨天忘更新了......讲的内容不多,就一个NAT。 之前记的NAT的内容:blog.csdn.net/Yisitelz/article/details/131840119 网络安全实训-网络工程 NAT 公网地址与私网地址 公网地址 可以在互联网上被寻址,由运营商统一分配全球唯一的I…...

【Unity入门】详解Unity中的射线与射线检测
目录 前言一、射线的创建方法二、射线检测1、Raycast()Raycast()不使用射线RayRaycast()使用射线Ray 2、RaycastAll()使用射线RayRaycastAll() 不使用射线Ray 3、射线的碰撞信息 三、示例四、具体使用场景射线的调试方法1、Debug.DrawLine()2、Debug.DrawRay利用Gizmos 前言 碰…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
