D-Star 寻路算法
D-Star 寻路算法
下面简写 D-Star 为 D*
-
D算法:D 算法”的名称源自 Dynamic A Star,最初由Anthony Stentz于“Optimal and Efficient Path Planning for Partially-Known Environments”中介绍。它是一种启发式的路径搜索算法, 适合面对周围环境未知或者周围环境存在动态变化的场景。
-
同 A算法类似,D 通过维护一个优先队列 OpenList 来对场景中的路径节点进行搜索,不同的是 D* 不是从起点节点开始搜索,而是从目标点开始搜索,首先将目标点放置进OpenList开始搜索,直到起点节点从OpenList队列中出队为止,即为搜索完成,否则视为搜索失败。
-
D*算法采用反向搜索的目的在于后期需要重新规划路径的时候,能够用到之前搜索到的最短路径信息,减少搜索量,以为从目标节点到起始节点进行搜索得到的最短路径,是以目标点为中心辐射出的最短路径图,图上目标点到各个点之间的路径都是最短的,因此当在既定路径上遇到障碍需要重新规划路径的时候,可以很好的利用之前得到的信息。
-
而从起点节点向目标节点搜索得到的最短路径图,是以起点为中心辐射出的最短路径图,当沿着路径前行遇到障碍后,需要重新进行路径规划时,没有办法很好的利用原先搜索到的信息。
-
E-Star 算法分为两个阶段
第一个阶段:使用 Dijkstra/A*算法找到从目标点到起始点的路径,然后机器人从开始节点向目标点移动。
第二阶段:是动态避障搜索阶段,当机器人移动到一个节点要向下一给节点移动的时候,发现下一个节点由可行走变成障碍时,需要重新规划路径。 -
参考D论文
D算法有几个重要的概念及函数
6.1. G : Goal State目标节点6.2. **State :**路径节点,路径节点包含以下几个信息
6.2.1. BackPointer:指向前一个 State 的指针,一般 Dijkstra/A 用 Parent表示,路径搜索结束后,机器人从所在的 State,通过 BackPointer 即可一步一步地移动到目标 Goal State
6.2.2. b(X) = Y 表示 X 的BackPointer*(父节点)是 Y
6.2.3. New:该State 从未被放置于 OpenList 中
Open:该State 此时正存放于 OpenList中
**Closed:**该 State 已经从 OpenList 中出队6.3. H(X):代价函数,表示当前 State 到 G 的开销计算,如果节点X的父节点是Y,H(X) = H(Y) + C(X,Y)
6.4. K(X):Key Function,该值是优先队列OpenList中的排序依据,K 值最小的State位于队列头(Dijkstra/A中 OpenList 排序是以H值为排序依据),D是针对动态环境设计的算法,由于环境的改变节点的H值可能发生改变,而节点的K值记录的是该点的最小H值,也就是说对于为遍历到的点,K=H=inf,对于表示为 Open或Closed的节点 K = min(K,H_new)
6.5. C(X,Y):表示X与Y之间的路径开销
注意:OpenList 是依据节点K值由小到大进行排序的优先队列
-
算法最主要的函数:
PROCESS-STATE:计算到目标G的最优路径
MODIFY-COST:改变两个 State 之间的开销C(X,Y),并将受影响的State置于OpenList 中
INSERT: 用来修改节点 X 状态以及 H(X)值和K(X)
D* 寻路算法伪代码如下
下面代码是论文中的代码

下面是代码的注释翻译
-- 下面代码包含:
-- 开始寻路过程
-- 行走过程
-- 遇到障碍再寻路的过程
{-- 初始设置目标节点 H 值为 0,将 G 加入到 OpenListh(G)=0;-- 开始寻路过程do{-- 循环调用 PROCESS-STATE(), 函数返回当前 OpenList 优先队列中节点K值最小的K值-- 如果 OpenList 优先队列中没有节点则返回 -1kmin=PROCESS-STATE();-- while 判定条件-- kmin = -1:说明还没有找到 开始节点(start state),OpenList 优先队列中没有节点了,则寻路失败-- start state not removed from open list:开始节点(start state)从 OpenList 队列出队,则已经从目标节点找到 开始节点了}while(kmin != -1 && start state not removed from open list);if(kmin == -1){-- 如果 kmin = -1 说明寻路失败返回,退出goal unreachable; exit;}else{-- 寻路成功,在 do-while 中包含了 行走、do{-- 行走过程do{-- 迭代行走trace optimal path();-- while 判定条件-- goal is not reached:没有到大 G 目标节点-- map == environment:假如当前走到节点X,要向下一个节点Y行走时,判断节点Y状态发生了变化(变成了障碍等)}while ( goal is not reached && map == environment);-- 如果已经到大 G 目标点,退出if (goal_is_reached){exit;}else{-- 没有到达目标点,肯定是行走过程中一个本来可以通过的节点,状态发生了变化-- 机器人行走过程中发现障碍时所在的 state 节点X-- 向节点Y行走时发现节点Y状态发生变化了,导致路径开销的更改已经传播到了节点XY = State of discrepancy reached trying to move from some State X;-- 改变节点Y、X 的CostMODIFY-COST(Y,X,newc(Y,X));-- 遇到障碍再寻路的过程do{kmin=PROCESS-STATE();-- while 判定条件-- kmin< h(X):经过不断地处理直到 kmin 小于节点 X 的 H值-- kmin != -1:当 kmin = -1 时表示寻路失败}while(kmin< h(X) && kmin != -1);-- 寻路失败,退出if(kmin==-1)exit();}}while(1);}
}
另论文中另一个版本的逻辑如下

两者的不同在于遇到障碍重新规划路径的 do-while 中的 while 部分
两个代码不同点只在下面 while 部分,经过测试,两种判定都是可以完成再次寻路的,时间原因论文没有仔细阅读,有疑问的读着可以自行去看论文,然后给我说一下结果
do
{kmin=PROCESS-STATE();
}while(kmin< h(X) && kmin != -1);do
{kmin=PROCESS-STATE();
}while( k(Y) < h(Y) && kmin != -1);
PROCESS-STATE() 函数

MODIFY-COST(X,Y,cval)
MIN-STATE()
GET-KMIN()
INSERT(X, newCost)

上面截图中函数代码不全,下面是各个函数补齐
MODIFY-COST(X,Y,cval)
c(X,Y)=cvalh(Y) = cvalif t(X) =CLOSED then INSERT (X,h(X))Return GET-MIN ( )
INSERT(X,Hnew)
if t(X) = NEW thenk(X)=hnew -- 然后就是 X 加入到 OpenList 队列这部分X and to OpenListif t(X) = OPEN then k(X)=min(k(X),hnew)if t(X) = CLOSED then k(X)=min(k(X),hnew)-- 然后就是 X 加入到 OpenList 队列这部分X and to OpenList-- 漏掉了 h(X) = hnewh(X) = hnewt(X)= OPENSort open list based on increasing k values;
MIN-STATE()
返回 OpenList 优先队列中 节点K 值最小的 节点
GET-KMIN()
返回 OpenList 优先队列中 节点K 值最小的 节点的 K 值
D* 核心逻辑就是上面几个截图
Originally stated D* Algorithm 或者 D* Algorithm, again
加 下面几个方法
PROCESS-STATE()
MODIFY-COST(X,Y,cval)
MIN-STATE()
GET-KMIN()
INSERT(X, newCost)
一个 使用 Unity 实现的 Demo 链接
算法在路径 PathFindingUnity\Assets\Script\PathFinding\Algorithms\DStar
效果如下

相关文章:

D-Star 寻路算法
D-Star 寻路算法 下面简写 D-Star 为 D* D算法:D 算法”的名称源自 Dynamic A Star,最初由Anthony Stentz于“Optimal and Efficient Path Planning for Partially-Known Environments”中介绍。它是一种启发式的路径搜索算法, 适合面对周围环境未知或者…...

mysql5.7编译安装
MySQL 5.7在不同操作系统上的编译安装过程略有不同,以下是在Linux系统上编译安装MySQL 5.7的一般步骤: 1. 安装编译所需的依赖包 sudo yum install gcc-c cmake ncurses-devel bison openssl-devel 2. 下载MySQL源码包和Boost库并解压 wget https://dev.mysql.com/get/Dow…...

Java项目实战记录:雷达数据渲染
目录 Java项目实战记录:雷达数据渲染业务背景代码逻辑数据结构颜色渲染MapContent加载数据并输出截图 完整代码GenerateMapImage地图渲染工具测试代码 渲染效果 Java项目实战记录:雷达数据渲染 业务背景 我之前已经成功使用Java语言解析了C处理的雷达数…...

进程的概念 | PCB | Linux下的task_struct | 父子进程和子进程
在讲进程之前首先就是需要去回顾一下我们之前学的操作系统是干嘛的,首先操作系统是一个软件,它是对上提供一个良好高效,稳定的环境的,这是相对于用户来说的,对下是为了进行更好的软硬件管理的,所以操作系统…...
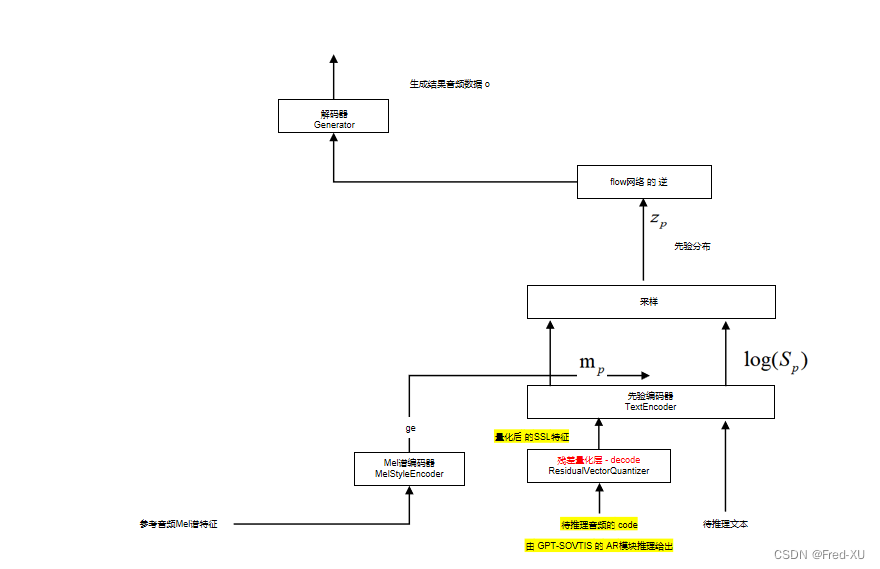
【GPT-SOVITS-03】SOVITS 模块-生成模型解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...

2024HVV行动-进军蓝中研判(log4j2、fastjson、Struts2、Shiro)
1、log4j2 特征: 恶意请求中包含 JNDI 协议地址,如"ldap://"、"rmi://"等,被 log4j2 解析为 JNDI 查找。 原理: 在日志输出中,未对字符进行严格的过滤,执行了 JNDI 协议加载的远程恶…...

亮点抢先看!4月16-17日,百度Create大会开设“AI公开课”,大咖带你打造赚钱工具
3月16日,2024百度Create AI开发者大会正式开放售票,嘉宾套票定价399元。据悉,本次大会以“创造未来(Create the Future)”为主题,设有20深度论坛、超30节AI公开课、3000平AI互动体验区和AI音乐节等精彩环节…...
【笔记本清灰/实用经验】荣耀Magicbook14-2020款-R5-4500U-清灰实战
清灰有风险,动手需谨慎,本文只分享本人的清灰过程,对使用它所产生的任何后果不任何负责任 文章目录 背景信息准备阶段工具准备信息收集 正式清灰初始化清灰流程放掉身体的静电(重要)拆笔记本后盖断开电源(重…...

如何写好Stable Diffusion的prompt
Stable Diffusion是一种强大的文本到图像生成模型,其效果在很大程度上取决于输入的提示词(Prompt)。以下是一些关于如何编写有效的Stable Diffusion Prompt的秘诀: 明确描述:尽量清晰地描述你想要的图像内容。使用具体…...

计算机毕业设计 | SpringBoot+vue 移动端社区物业管理系统(附源码+论文)
1, 概述 课题背景 近几年来,随着物业相关的各种信息越来越多,比如报修维修、缴费、车位、访客等信息,对物业管理方面的需求越来越高,我们在工作中越来越多方面需要利用网页端管理系统来进行管理,我们所需…...
玩转C语言——数组初探
一、前言 通过前面的学习,我们已了解C语言的结构变量、分支结构和循环结构。今天,我们一起来认识C语言的另一知识点——数组。先赞后看,养成习惯。 二、数组概念 学习数组,我们要明白数组是什么。在我看来:数组是⼀组…...

Nginx指令配置大全
基本命令 nginx -t 检查配置文件是否有语法错误 nginx -s reload 热加载,重新加载配置文件 nginx -s stop 快速关闭 nginx -s quit 等待工作进程处理完成后关闭配置块介绍 全局块 全局块是默认配置文件从开始到events块之间的…...

富格林:安全出金关注可信操作
富格林悉知,现货黄金投资凭借着诸多优势,成为了热门的投资产品之一,也获得了投资者的追捧。在投资中想要安全盈利出金,投资者一定要沉下心来学习专业知识和技术,这样才能在以后的投资操作中避免亏损,顺畅盈…...

DELETE、TRUNCATE 和 DROP 在MySQL中的区别及使用示例
在MySQL数据库中,DELETE、TRUNCATE TABLE 和 DROP 这三个命令分别适用于不同的数据删除需求,它们在工作原理、应用场景以及特性上有所区别。接下来,我们通过实例演示来明确这三者的不同之处。 DELETE 命令 功能与示例:DELETE 语…...

程序员应该如何选择职业赛道?
程序员选择职业赛道是一个涉及个人兴趣、技能匹配、市场需求和长远发展规划的综合决策过程。以下是一些关键步骤和考虑因素: 自我评估: 技能与专长:分析自己在编程语言、算法、数据结构等方面的现有技能,并思考这些技能更适合前端…...

深入浅出Hive性能优化策略
我们将从基础的HiveQL优化讲起,涵盖数据存储格式选择、数据模型设计、查询执行计划优化等多个方面。会的直接滑到最后看代码和语法。 目录 引言 Hive架构概览 示例1:创建表并加载数据 示例2:优化查询 Hive查询优化 1. 选择适当的文件格…...

利用卷积神经网络进行人脸识别
利用卷积神经网络(Convolutional Neural Networks, CNNs)进行人脸识别是计算机视觉领域的一个热门话题。下面是一个简化的指南,涵盖了从理论基础到实际应用的各个方面,可以作为你博文的基础内容。 理论基础 卷积神经网络简介&am…...

固态硬盘有坏道怎么恢复数据 固态硬盘坏道怎么修复
固态硬盘是一种高速、低噪音、低功耗的存储设备,但是它也有一个致命的问题——坏道。坏道是指存储芯片中的某些存储单元出现了故障,导致数据无法正常读取或写入。如果你的固态硬盘出现了坏道,那么你的数据就有可能会丢失,带来了很大的困扰。那么,固态硬盘有坏道怎么恢复数…...
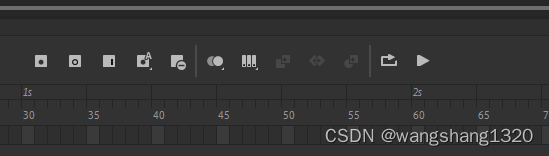
adobe animate 时间轴找不到编辑多个帧按钮
如题,找了半天,在时间轴上找不到编辑多个帧按钮,导致无法批量处理帧 然后搜索发现原来是有些版本被隐藏了,需要再设置一下 勾选上就好了...

5 亿欧元巨额奖励!法国国防部启动量子初创公司项目
内容来源:量子前哨(ID:Qforepost) 编辑丨王珩 编译/排版丨沛贤 深度好文:800字丨6分钟阅读 据C4ISNET报道,法国国防部采购机构宣布向五家法国量子计算研究初创公司授予合同,用于开发量子计算技…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
