力扣● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 编辑距离总结篇
● 583. 两个字符串的删除操作
注意审题:
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
删除最少的字符使两者相同,说明留下来的就是最大公共子序列。不要求连续,所以可以使用● 1143.最长公共子序列 来做,最长公共子序列之外的字母都要删除,所以返回 (n1+n2-2*dp[n1][n2]) 即可。
这是间接求法,直接求:
1.dp数组含义。
dp[i][j]:以word1[i-1]为结尾的字符串,和以word2[j-1]位结尾的字符串,想要达到相等,所需要删除元素的最少次数为dp[i][j]。
2.递推公式。
如果相等:删除次数要最少,那么相等的话就不能删除,得留着,所以dp[i][j]=dp[i-1][j-1];
如果不等:2个字符串没有谁长谁短的前提,所以应该有3种情况。
①可能删掉word1[i-1],那么dp[i][j]代表的子序列和dp[i-1][j]代表的子序列删除的字母,就多了一个:word1[i-1],所以dp[i][j]=dp[i-1][j]+1;
②可能删掉word2[j-1],同样,dp[i][j]=dp[i][j-1]+1;
③都删除。都删除的话,dp[i][j]代表的子序列和dp[i-1][j-1]代表的子序列删除的字母,就多了2个:word1[i-1]和word2[j-1],所以是dp[i][j]=dp[i-1][j-1]+2;这其实也是满足情况①和情况②的,删掉2个,和dp[i-1][j]相比多删了一个word2[j-1],和dp[i][j-1]相比多删了一个word1[i-1]。所以情况①/情况②就把③包含了。所以只取①和②的最小删除数量,即Min值就是对的。
dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);
3.初始化。
dp[i][0]。i>0时,word1[i-1]:非空串;word2[0,-1]:空串。所以应该删除word1的前i个达到相等。
dp[0][j]。同样应该删除word2的前j个达到相等。
dp[0][0]。不用删除,=0。
4.遍历顺序。
5.打印。
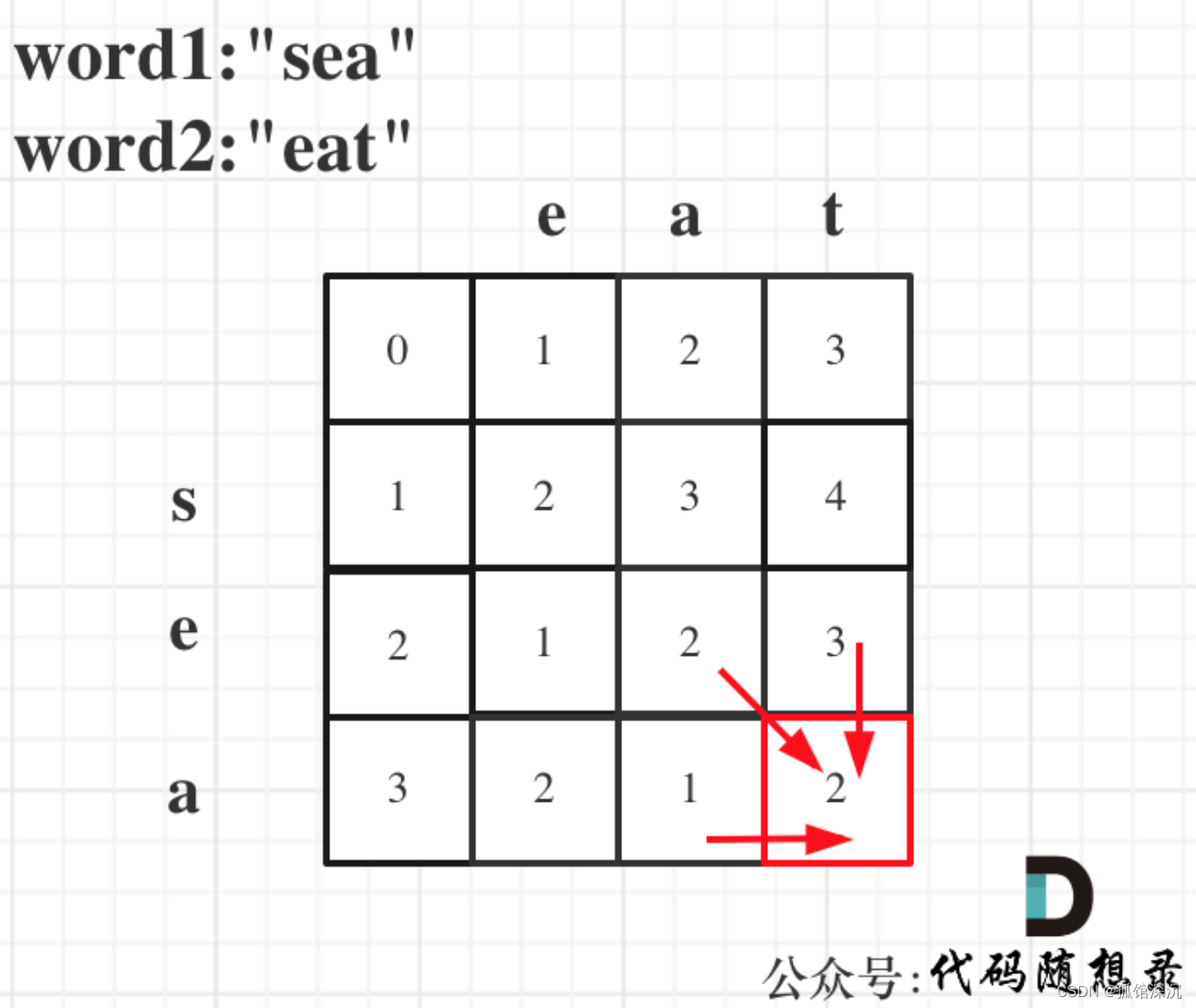
代码如下:
class Solution {
public:int minDistance(string word1, string word2) {int n1=word1.size();int n2=word2.size();vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));for(int i=1;i<=n1;++i)dp[i][0]=i;for(int j=1;j<=n2;++j)dp[0][j]=j;for(int i=1;i<=n1;++i){for(int j=1;j<=n2;++j){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1];}else{dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//省略dp[i-1][j-1]+2;}}}return dp[n1][n2];}
};
● 72. 编辑距离
1.dp数组含义。
dp[i][j]:数组1[0,i-1]中操作(插删换)dp[i][j]次,得到的序列是数组2[0,j-1]。注意这个操作过程是可逆的,2[0,j-1]中操作(删插换)dp[i][j]次,得到的序列是1[0,i-1]。
所以每一步操作,既可以对数组1操作,也可以对数组2操作。我觉得变换一下题目解法也没有变:请返回操作后使word1和word2相同的最大操作数。
举例:“horse”变成“ros”:
horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
因为,对数组1 的 插入 等同于对数组2 的删除,删除同理,那么:
ros -> rose (插入 'e');horse-> rorse(将 'h' 替换为 'r');rose -> rorse(插入 'r')。
即中间每步可以选择对1操作,也可以对2操作。可见操作后可以得到很多种相同字符串(horse、rorse、rose或ros),但是过程中数组1和数组2操作的次数之和是固定的,即编辑距离是固定的。
2.递推公式。
(1)不相等的话,这3个操作都有可能发生,那么是肯定要加上1(做一个操作)。
①替换:
可以1[i-1]替换成2[j-1],也可以2[j-1]替换成1[i-1]。改了之后,得到的2个子数组最后元素相同,所以应该是在dp[i-1][j-1]的基础上替换了1或2的一个元素,所以+1。
即dp[i][j]=dp[i-1][j-1]+1。
②可以删除:
删除1[i-1]达到相同,说明[0,i-2]中操作之后,就能得到2[0,j-1]了,所以是在这个基础(dp[i-1][j])之上加一个删除操作即可,即dp[i][j]=dp[i-1][j]+1。
也可以删除2[j-1]达到相同,那么同理,dp[i][j]=dp[i][j-1]+1。
③可以插入:
插入1[i-1]达到相同,代表着删除2[i-1]达到相同,上面说了只是操作不同但次数相同,所以在1或2插入的情况都可以用删除表示,所以1[i-1]后面插入的情况下dp[i][j]==dp[i][j-1]+1。2[j-1]后面插入的情况下dp[i][j]=dp[i-1][j]+1。上面都包含了。
所以:dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
(2)相等:和上题同样是求最少操作数,所以相等的话不操作,即dp[i][j]=dp[i-1][j-1]。
3.初始化。
回忆dp的含义:
dp[i][0]=i。以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
dp[0][j]=j。同理。
4.遍历顺序。
从上到下,从左到右。
5.打印。
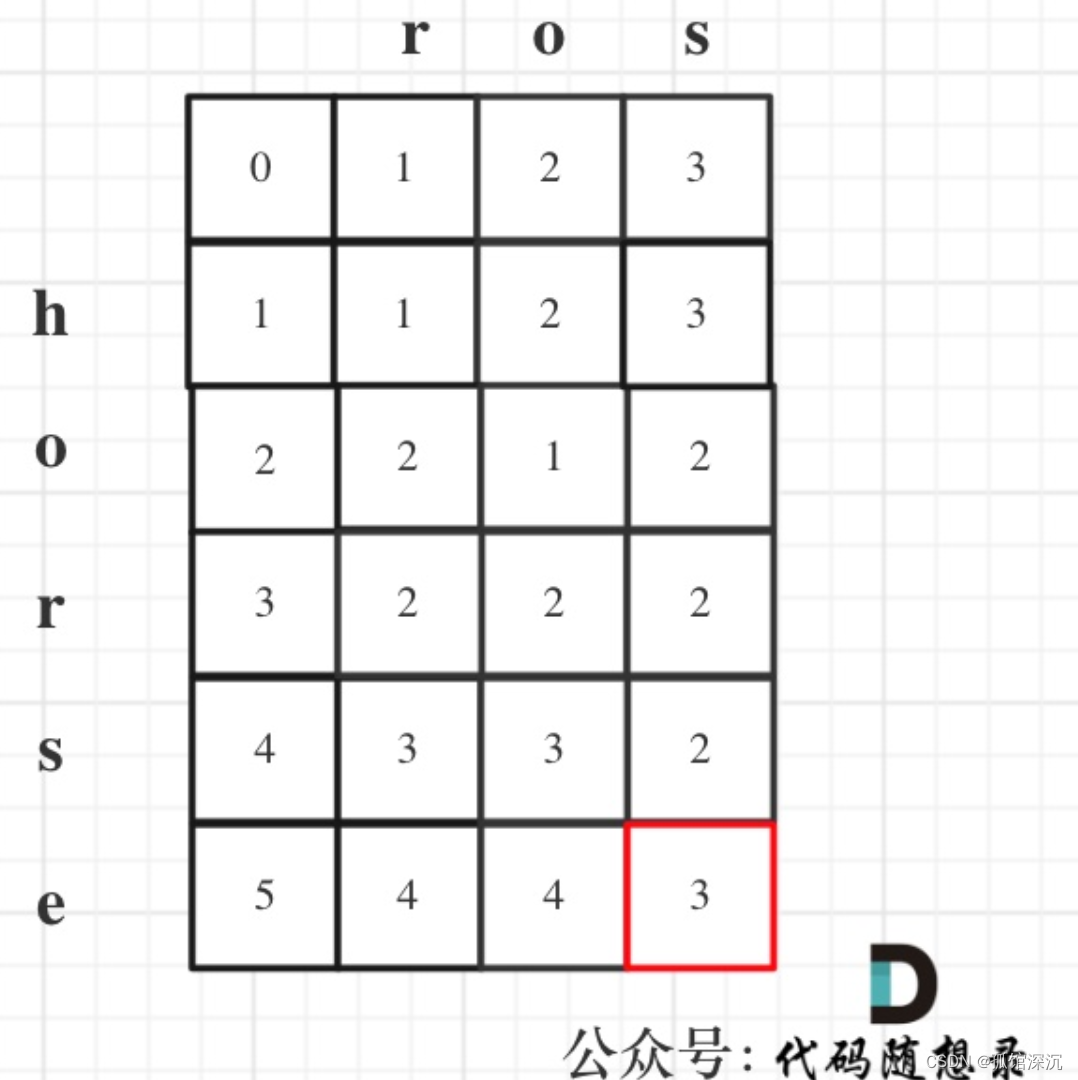
代码如下:
class Solution {
public:int minDistance(string word1, string word2) {int n1=word1.size();int n2=word2.size();vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));for(int j=0;j<=n2;++j)dp[0][j]=j;//删除for(int i=0;i<=n1;++i)dp[i][0]=i;//插入for(int i=1;i<=n1;++i){for(int j=1;j<=n2;++j){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1];}else{dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;//,}}}return dp[n1][n2];}
};
● 编辑距离总结篇
做多了总结一下:都是在dp[i-1][j-1]、dp[i-1][j]、dp[i][j-1]的基础上得到dp[i][j],要得到这个递推公式,就是得清楚,什么情况下,对A[i-1](B[j-1])做什么操作,比如上面● 72. 编辑距离,不相同的话,可能对A[i-1]和B[j-1]这一对,修改其中一个就行,所以是在dp[i-1][j-1]基础上+1……
总结一下3个编辑距离前导题:
判断子序列
判断s是不是t的子序列。根据最长公共子序列来做,dp[i][j]不要求si-1、t[j-1]结尾。
2个元素相等的时候。dp[i][j]=dp[i-1][j-1]+1;
不相等。因为序列1一定比序列2短,不相等的话dp[i][j-1]一定大于dp[i-1][j],所以dp[i][j]=dp[i][j-1];
不同的子序列
统计序列s在序列t中出现的个数。
2个元素相同。s[i-1]有可能匹配t[j-1]以及t[j-1]之前的与之相等的元素。
所以dp[i][j]=dp[i-1][j-1]+dp[i-1][j-1];
不相同。s[i-1]只可能匹配t[j-1]之前的,所以dp[i][j]=dp[i-1][j]。
两个字符串的删除操作
统计序列s和序列t,删除最少几个元素变成一样。
相同。dp[i][j]=dp[i-1][j-1]
不同。省略了删除2个dp[i-1][j-1]+2。dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);
相关文章:

力扣● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 编辑距离总结篇
● 583. 两个字符串的删除操作 注意审题: 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 删除最少的字符使两者相同,说明留下来的就是最大公共子序列。不要求…...
Git速成
文章目录 Git 分布式版本控制工具课程内容1. 前言1.1 什么是Git1.2 使用Git能做什么 2. Git概述2.1 Git简介2.2 Git下载与安装 3. Git代码托管服务3.1 常用的Git代码托管服务3.2 码云代码托管服务3.2.1 注册码云账号3.2.2 登录码云3.2.3 创建远程仓库3.2.4 邀请其他用户成为仓库…...

一文看懂softmax loss
文章目录 softmax loss1.softmax函数2.交叉熵损失函数3.softmax loss损失函数(重点)4.带有temperature参数的softmax loss参考 softmax loss 1.softmax函数 softmax函数是一种常用的激活函数,通常用于多分类任务中。给定一个向量࿰…...

用C语言链表实现图书管理
#include <stdio.h> #include <stdlib.h> #include <string.h> struct ListNode {int val;//编号char title[50];//书名float price;//价格struct ListNode* next; };// 在尾部插入节点 struct ListNode* insertAtTail(struct ListNode* head, int val,char …...
Hello,Spider!入门第一个爬虫程序
在各大编程语言中,初学者要学会编写的第一个简单程序一般就是“Hello, World!”,即通过程序来在屏幕上输出一行“Hello, World!”这样的文字,在Python中,只需一行代码就可以做到。我们把这第一个爬虫就称之为“HelloSpider”&…...
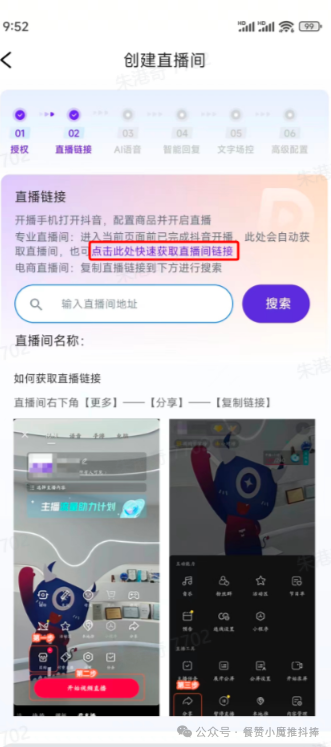
AI实景无人自动直播间怎么搭建?三步教你轻松使用
最近很多朋友看到AI自动直播带货玩法,也想开启自己的自动直播间,但还是有些问题比较担心,这种自动讲解、自动回复做带货的直播间是不是很麻烦? 实景无人自动直播 实际上这种直播间搭建相当简单便捷!今天跟着笔者&…...
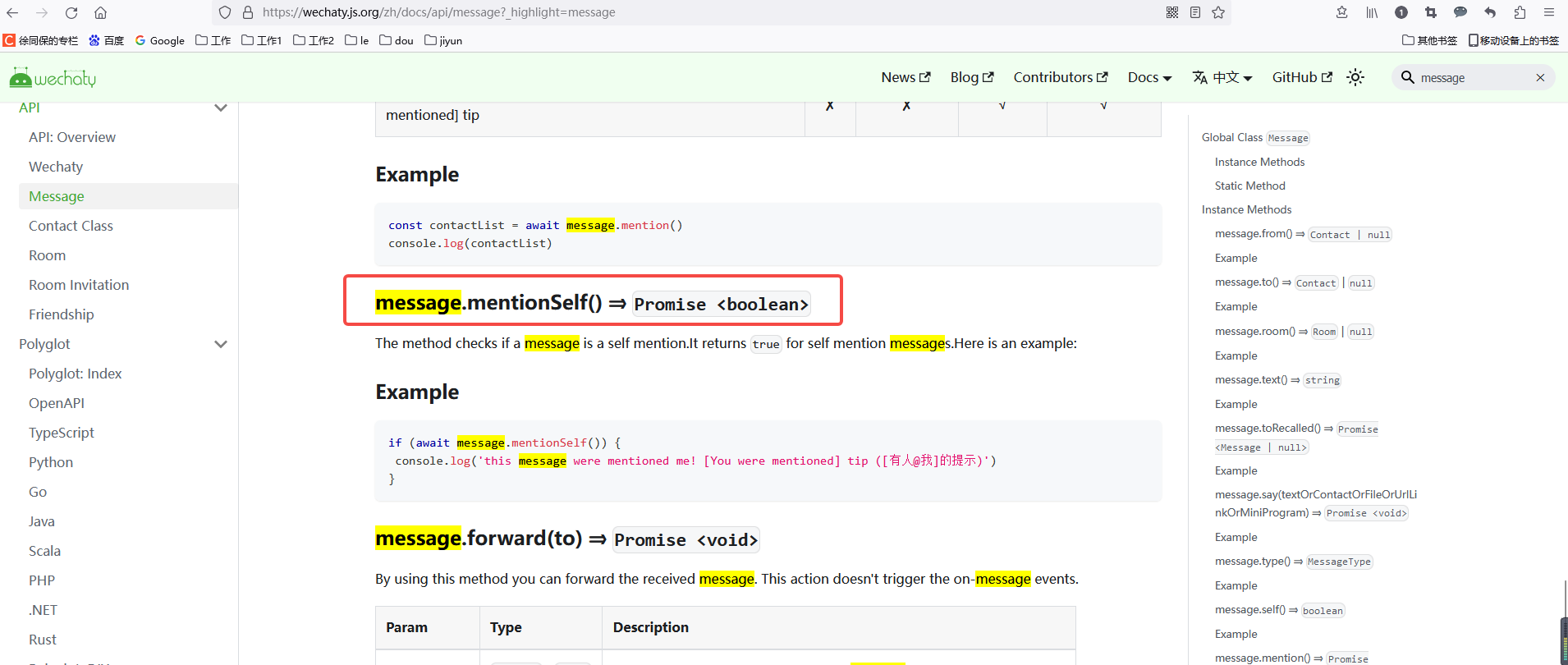
wechaty微信机器人,当机器人被@时做出响应
https://wechaty.js.org/zh/docs/api/message?_highlightmessage if (await msg.mentionSelf()) {console.log(this message were mentioned me! [You were mentioned] tip ([有人我]的提示))await room.say(不要微信机器人)} 我开发的人工智能学习网站: https://…...

8.6 Springboot项目实战 Spring Cache注解方式使用Redis
文章目录 前言一、配置Spring Cache1. @EnableCaching2. 配置CacheManager3. application.properties配置二、使用注解缓存数据1. 使用**@Cacheable** 改造查询代码2. 使用**@CacheEvict** 改造更新代码前言 在上文中我们使用Redis缓存热点数据时,使用的是手写代码的方式,这…...
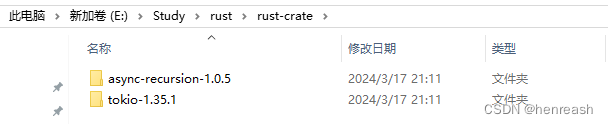
rust引用本地crate
我们可以动态引用crate,build时从crate.io下载,但可能因无法下载导致build失败。首次正常引用三方crate,build时自动下载的crate源码,我们将其拷贝到固定目录中; build后可在RustRover中按住Ctrl键,在crat…...

分布式(计算机算法)
目录 分布式计算 分布式编辑 分布式和集群 分布式和集群的应用场景 分布式应用场景 集群应用场景 哪种技术更优、更快、更好呢 性能 稳定性 以下概念来源于百度百科 分布式计算 分布式计算是近年提出的一种新的计算方式。所谓分布式计算就是在两个或多个软件互相共享信息…...

CSS概念及入门
文章目录 1. CSS 概念及入门1.1. 简介1.2. 组成1.2.1. 选择器1.2.2. 属性 1.3. 区别 2. CSS 引入方式2.1. 行内样式2.1.1. 语法2.1.2. 特点 2.2. 内部样式2.2.1. 语法2.2.2. 特点 2.3. 外部样式2.3.1. 特点 2.4. 三种引入优先级 1. CSS 概念及入门 1.1. 简介 CSS 的全称为&am…...

用 C 语言模拟 Rust 的 Result 类型
在 Rust 中,Result<T, E> 类型是一个枚举,它表示一个操作可能成功并返回一个值 T,或者失败并返回一个错误 E。在 C 语言中,没有直接对应的 Result 类型,但我们可以使用结构体和枚举来模拟它。 下面是一个用 C 语…...
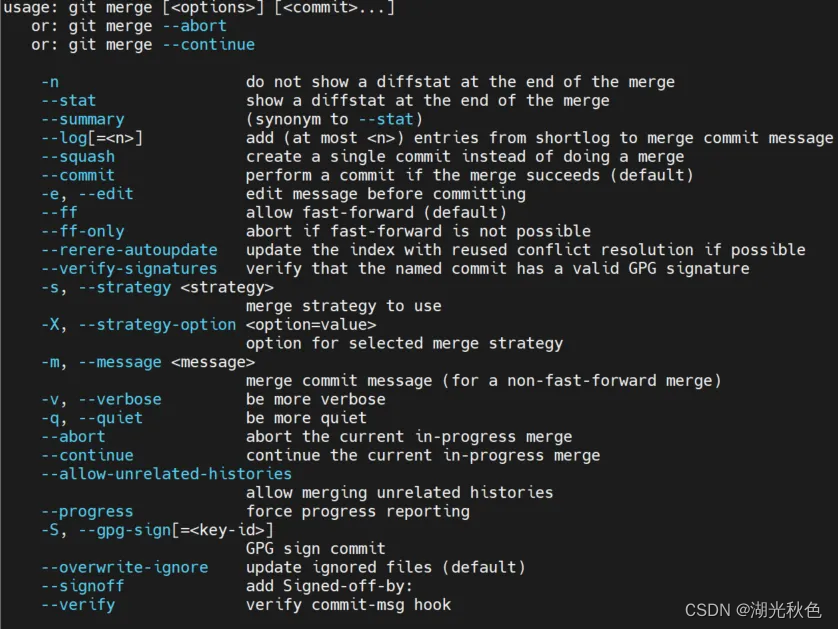
git基础命令(四)之分支命令
目录 基础概念git branch-r-a-v-vv-avv重命名分支删除分支git branch -h git checkout创建新的分支追踪远程分支同时切换到该分支创建新的分支并切换到该分支撤销对文件的修改,恢复到最近的提交状态:丢弃本地所有修改git checkout -h git merge合并指定分…...
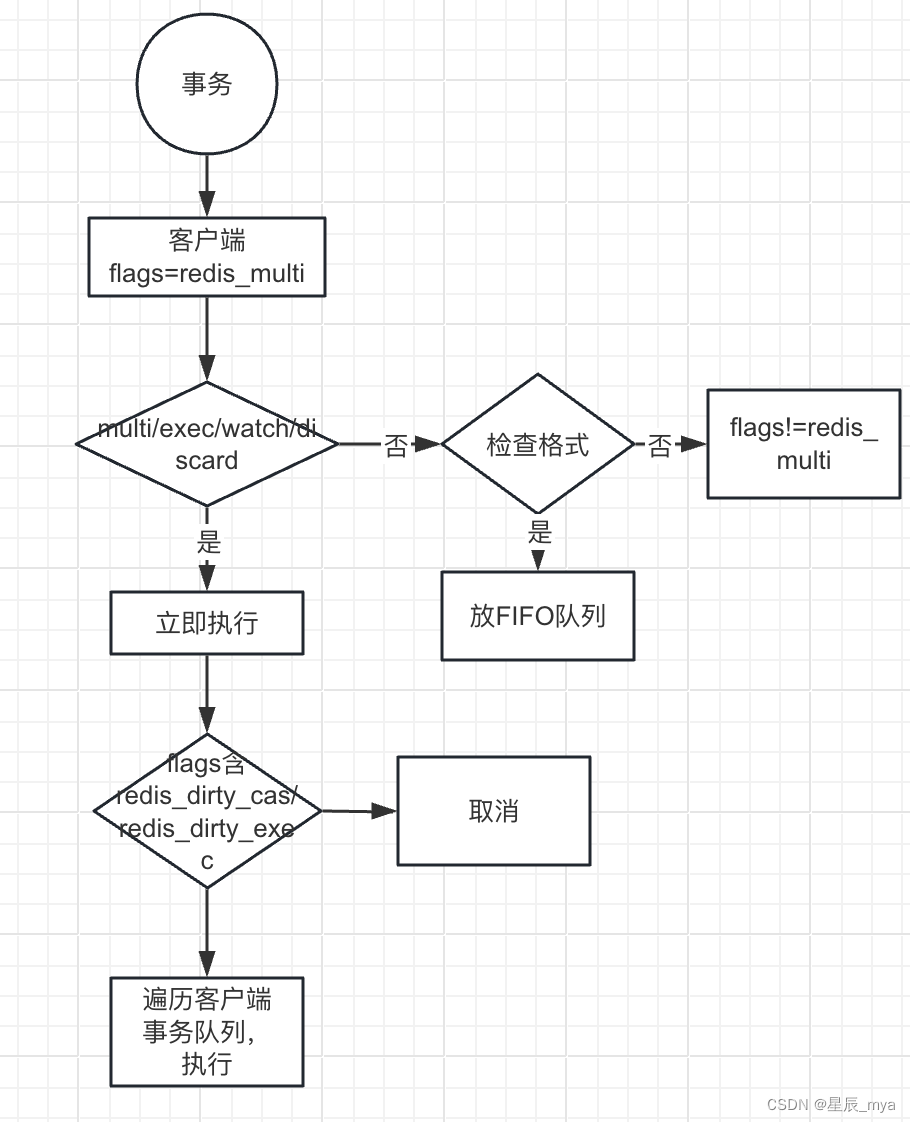
redis瘦身版
线程模型 纯内存操作/非阻塞io多路复用/单线程避免多线程频繁上下文切换 基于Reactor模式开发了网络事件处理器:文件事件处理器,单线程的 io多路监听多个socket,据socket事件类型选择对应的处理器,高性能网络通信模型,…...
使用ChatGPT高效完成简历制作[中篇]-有爱AI实战教程(五)
演示站点: https://ai.uaai.cn 对话模块 官方论坛: www.jingyuai.com 京娱AI 导读:在使用 ChatGPT 时,当你给的指令越精确,它的回答会越到位,举例来说,假如你要请它帮忙写文案,如果没…...
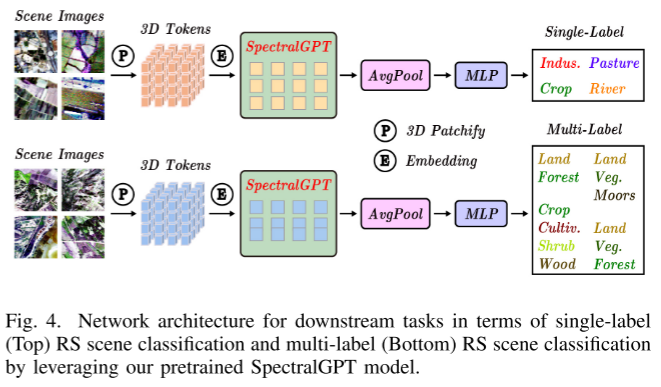
论文阅读——SpectralGPT
SpectralGPT: Spectral Foundation Model SpectralGPT的通用RS基础模型,该模型专门用于使用新型3D生成预训练Transformer(GPT)处理光谱RS图像。 重建损失由两个部分组成:令牌到令牌和频谱到频谱 下游任务:...

Redis的过期键是如何处理的?过期键的删除策略有哪些?请解释Redis的内存淘汰策略是什么?有哪些可选的淘汰策略?
Redis的过期键是如何处理的?过期键的删除策略有哪些? Redis的过期键处理是一个重要的内存管理机制,它确保在键过期后能够释放相应的内存空间。Redis对过期键的处理主要依赖于其删除策略,这些策略包括被动删除(惰性删除…...

软件测试方法 -- 等价类边界值
测试用例的定义 测试用例是为了特定的目的而设计的一组测试输入、执行条件和预期的结果,以便测试是否满足某个特定需求。通过大量的测试用例来检验软件的运行效果,他是指导测试工作进行的依据。 下面我们介绍几种常用的黑盒测试方法 等价类划分法 定…...

LeetCode——贪心算法(Java)
贪心算法 简介[简单] 455. 分发饼干[中等] 376. 摆动序列[中等] 53. 最大子数组和[中等] 122. 买卖股票的最佳时机 II[中等] 55. 跳跃游戏 简介 记录一下自己刷题的历程以及代码。写题过程中参考了 代码随想录的刷题路线。会附上一些个人的思路,如果有错误…...
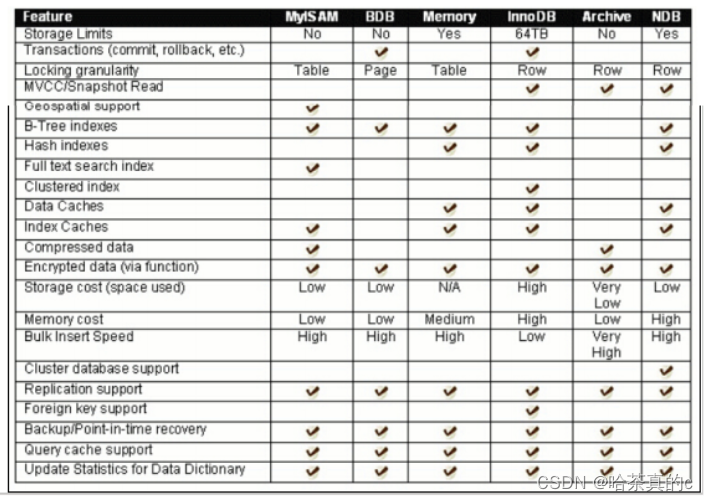
【MySQL】2. 数据库基础
1. 数据库基础(重点) 1.1 什么是数据库 存储数据用文件就可以了,为什么还要弄个数据库? 文件保存数据有以下几个缺点: 文件的安全性问题 文件不利于数据查询和管理 文件不利于存储海量数据 文件在程序中控制不方便 数据库存储介…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
