当前位置： 首页 > news >正文

Java毕业设计 基于springboot vue招聘网站 招聘系统

news 文章来源：https://blog.csdn.net/yinjl123/article/details/136818649 2025/5/5 5:25:14

Java毕业设计 基于springboot vue招聘网站 招聘系统

springboot vue招聘网站 招聘系统 功能介绍

用户：登录 个人信息 简历信息 查看招聘信息

企业：登录 企业信息管理 发布招聘信息 职位招聘信息管理 简历信息管理

管理员：注册 登录 管理员管理 用户管理 企业管理 简历信息管理 招聘信息管理

角色：用户 企业 管理员

开发环境和技术

  • 开发语言：Java

  • 使用框架: SpringBoot + Mybaits

  • 前端: vue

  • 数据库：Mysql

  • 架构：B/S

  • 源码类型： Web

  • 编译开发工具：Idea、Eclipse、MyEclipse (选其一)

  • 其他：jdk1.8

功能图片展示

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

后台运行

idea导入项目

创建数据库

使用navicat导入sql表结构和数据

修改resources目录下 application.yml 配置文件的mysql的ip和帐号和密码连接信息

启动 Application 类的main方法

vue运行

nom install 安装依赖

npm run serve 运行

Nom run build 编译

总结

源码获取：

大家可点赞、收藏、关注、评论、私信

相关文章：

Java毕业设计 基于springboot vue招聘网站 招聘系统

Java毕业设计 基于springboot vue招聘网站 招聘系统 springboot vue招聘网站 招聘系统 功能介绍 用户：登录 个人信息 简历信息 查看招聘信息 企业：登录 企业信息管理 发布招聘信息 职位招聘信息管理 简历信息管理 管理员：注册 登录 管理员…...

编程日记 2024/3/18 20:47:40

Leetcode 1. 两数之和

心路历程： 很简单的题，双层暴力就可以，用双指针的话快一点。暴力时间复杂度O( n 2 n^2 n2)，双指针时间复杂度O(nlogn) O(n) O(n) O(nlogn)。 注意的点： 1、题目需要返回原数组的索引，所以排序后还需要…...

编程日记 2024/3/18 20:46:39

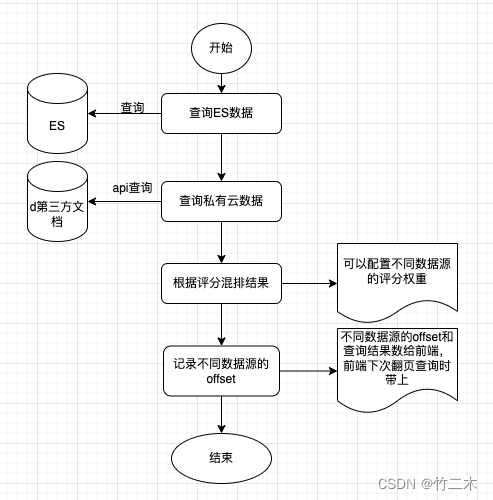
【elasticsearch实战】从零开始设计全站搜索引擎

业务需求 最近需要一个全站搜索的功能，我们的站点的特点是数据多源，即有我们本地数据库，也包含了第三方数据源，我们的数据类型除了网页，还包括了各种类型的文档，例如：doc、pdf、excel、ppt等格…...

编程日记 2024/3/18 20:45:38

基于tcp协议的网络通信(基础echo版.多进程版,多线程版,线程池版),telnet命令

目录 基础版 思路 辅助函数 服务端 代码 运行情况 -- telnet ip 端口号 传输的数据为什么没有转换格式 客户端 思路 代码 多进程版 引入 问题 解决 注意点 服务端 代码 运行情况 进程池版(简单介绍) 多线程版 引入 问题解决 注意点 服务端 代码 …...

编程日记 2024/3/18 20:43:36

Ubuntu20系统安装完后没有WIFI

Ubuntu20系统安装完后没有WIFI 查看后发现是缺少网卡&#xff0c;经过查询之后&#xff0c;发现是HRex39/rtl8852be 然后查询了Kernel版本 Check the Kernel Version in Linux $ uname -srm Linux 5.15.0-67-generic x86_64然后进行下载安装 Build(for kernel < 5.18) …...

编程日记 2024/3/18 20:40:33

计算机视觉——目标检测（R-CNN、Fast R-CNN、Faster R-CNN ）

前言、相关知识 1.闭集和开集 开集&#xff1a;识别训练集不存在的样本类别。闭集&#xff1a;识别训练集已知的样本类别。 2.多模态信息融合 文本和图像&#xff0c;文本的语义信息映射成词向量&#xff0c;形成词典&#xff0c;嵌入到n维空间。 图片内容信息提取特征&…...

编程日记 2024/3/18 20:38:31

log4j2.xml配置文件不生效

问题 使用springboot配置log4j2&#xff0c;添加了依赖并排除默认的logging依赖&#xff0c;配置了log4j2.xml文件&#xff0c;放在scr目录下&#xff0c;运行可以在控制台输出日志&#xff0c;但不受配置文件影响 解决 配置文件log4j2.xml放在resources目录下生效...

编程日记 2024/3/18 20:36:29

QT信号与槽实现方式

1、第一种实现方式 在QT开发工具UI界面先拖入按钮&#xff0c;然后鼠标右键拖入按钮&#xff0c;点击选中槽&#xff0c;在页面选着需要的信号&#xff0c;然后OK&#xff0c;随即将会跳转到类的.cpp文件&#xff0c;&#xff08;这种UI代码结合的方式&#xff0c;会自动去绑定…...

编程日记 2024/3/18 20:35:28

Yarn面试重点

文章目录 1. 简述Yarn集群的架构2. Yarn 的任务提交流程是怎样的&#xff1f;3. yarn的资源调度的三种模型 1. 简述Yarn集群的架构 YARN&#xff08;Yet Another Resource Negotiator&#xff09;是Hadoop 2.x引入的资源管理器&#xff0c;用于管理Hadoop集群中的资源和作业调…...

编程日记 2024/3/18 20:34:27

高速口光口通信

1.通过transceiver ip 设置好硬件连接配置 2.open example 用自己的模块替换掉tx和rx数据模块 3.大小端问题—— 4.配置gt收发器的rx的k码时候需要设置anybyte便于高效率接收。 5.开发数据产生模块和接收校验模块都需要使用TXUSRCLK2,但是TXUSRCLK线速度/内部数据位宽。——…...

编程日记 2024/3/18 20:33:26

python--剑指offer--15. 二进制中1的个数

编写一个函数&#xff0c;输入是一个无符号整数&#xff08;以二进制串的形式&#xff09;&#xff0c;返回其二进制表达式中数字位数为 ‘1’ 的个数&#xff08;也被称为 汉明重量).&#xff09;。 提示&#xff1a; 请注意&#xff0c;在某些语言&#xff08;如 Java&…...

编程日记 2024/3/18 20:32:25

uniapp h5 部署

uniapp 配置 服务器文件路径 打包文件结构 //nginx 配置 server {listen 8300;server_name bfqcwebsiteapp;charset utf-8;#允许跨域请求的域&#xff0c;* 代表所有add_header Access-Control-Allow-Origin *;#允许带上cookie请求add_header Access-Control-Allow-C…...

编程日记 2024/3/18 20:31:24

排序算法：快速排序(递归)

文章目录 一、创始人托尼霍尔的快速排序二、挖坑法三、前后指针法 所属专栏:C初阶 引言&#xff1a;这里所说的快速排序有三种&#xff0c;第一种是霍尔大佬自创的&#xff0c;还有一种叫做挖坑法&#xff0c;另外一种叫前后指针法 一、创始人托尼霍尔的快速排序 1.这里我们先…...

编程日记 2024/3/18 20:30:22

蓝桥杯每日一题（BFS）

1562 微博转发 开始思路错误点&#xff1a;在用拉链法保存关注信息的时候&#xff0c;因为要看一个用户发的有多少转发的&#xff0c;所以要以用户为坑位&#xff0c;所有关注这个坑位的用户为链表。&#xff08;开始弄反了&#xff09; e数组存某个用户的idx&#xff0c;ne是…...

编程日记 2024/3/18 20:29:21

【C语言】linux内核pci_save_state

一、中文注释 //include\linux\pci.h /* 电源管理相关的例程 */ int pci_save_state(struct pci_dev *dev);//drivers\pci\pci.c /*** pci_save_state - 在挂起前保存PCI设备的配置空间* dev: - 我们正在处理的PCI设备*/ int pci_save_state(struct pci_dev *dev) {int i;/* X…...

编程日记 2024/3/18 20:28:20

轻松打造完美原型：9款在线工具推荐

早年&#xff0c;UI设计师选择的工具有限&#xff0c;功能相对单一&#xff0c;大多数在线原型设计工具都是国外的&#xff0c;语言和网络都增加了设计工作的负担。如今&#xff0c;国内外有许多在线原型设计工具&#xff0c;不仅可以在浏览器上使用&#xff0c;而且还具有团队…...

编程日记 2024/3/18 20:27:20

Vue3中Pinia状态管理库学习笔记

pinia的基本使用 <template><div><h2>Home View</h2> <h2>count:{{ counterStore.count }}</h2><h2>count:{{ count }}</h2><button click"increment">count1</button></div> </template>…...

编程日记 2024/3/18 20:26:18

共谋企业出海新篇章纷享销客荣获数字中国企业峰会“卓越成果奖”

3月9日&#xff0c;2024数字中国企业峰会在杭州西湖中维香溢大酒店成功举办&#xff0c;众多数字化领域专家、知名企业 CIO 代表到场。峰会旨在推动数字化转型与创新发展&#xff0c;为企业出海和国际合作搭建交流与合作的平台。本次峰会的颁奖环节&#xff0c;纷享销客凭借其卓…...

编程日记 2024/3/18 20:24:16

【MySQL】group_concat 函数和 locate 函数运用之找到每篇文章的主题

力扣题 1、题目地址 2199. 找到每篇文章的主题 2、模拟表 表&#xff1a;Keywords Column NameTypetopic_idintwordvarchar (topic_id, word) 是该表的主键&#xff08;具有唯一值的列的组合&#xff09;。该表的每一行都包含一个主题的 id 和一个用于表达该主题的词。可…...

编程日记 2024/3/18 20:20:13

RedisCluster集群中的插槽为什么是16384个？

RedisCluster集群中的插槽为什么是16384个&#xff1f; CRC16的算法原理。 1.根据CRC16的标准选择初值CRCIn的值2.将数据的第一个字节与CRCIn高8位异或3.判断最高位&#xff0c;若该位为0左移一位&#xff0c;若为1左移一位再与多项式Hex码异或4.重复3至9位全部移位计算结束5…...

编程日记 2024/3/18 20:19:12

一直出现问题，发现服务器磁盘空间已满导致，腾出服务器磁盘空间命令

要解决服务器磁盘空间已满的问题&#xff0c;你可以按照以下步骤操作&#xff1a; 查看磁盘使用情况&#xff1a;使用df -h&#xff0c; du -s -h ./*命令来查看服务器的磁盘空间使用情况。查找大文件&#xff1a;使用du -a | sort -rn | head -5命令来找出占用空间最大的前5个…...

编程日记 2024/3/18 20:18:10

吴恩达机器学习笔记 二十三 倾斜数据集的误差指标 精确率 召回率 精确率与召回率的平衡 F1分数

如果数据集的正例和反例的比例非常倾斜&#xff0c;常用的错误指标如 准确率(accuracy) 并不好用。此时可以用精确率和召回率。 精确率&#xff08;precision&#xff09;&#xff1a;真阳的样本数/预测为阳的样本数真阳数/&#xff08;真阳假阳&#xff09; 召回率(recall):…...

编程日记 2024/3/18 20:14:06

无人游艇的研发和开发对于多个领域具有重要

无人游艇的研发和开发对于多个领域具有重要性。 首先&#xff0c;无人游艇可以在海上进行各种任务&#xff0c;如海洋科学研究、资源勘探和监测、海洋环境保护等。相比传统的人工操作船只&#xff0c;无人游艇可以长时间在海上工作&#xff0c;可以自动化执行任务&#xff0c;…...

编程日记 2024/3/18 20:11:03

在AI创业热潮下，如何抓住AI赚钱机会，实现人生逆袭

随着人工智能技术的迅猛发展，AI创业热潮正席卷全球。这不仅为科技领域的专业人士提供了无限的商机，也为普通人开辟了全新的赚钱途径。本文将为您揭示在AI创业热潮下，普通人如何抓住AI赚钱机会，实现人生逆袭，同时探讨哪些行业适合应用AI技术。 一、普通人如何抓住AI赚钱机…...

编程日记 2024/3/18 20:09:01

JETSON 配置并跑通 NanoDet

JETSON 配置 NanoDet 文章目录 JETSON 配置 NanoDetNanoDet 介绍源码环境搭建及测试配置 NanoDet 的环境环境配置过程中遇到的问题&#xff1a;环境配置完毕验证 NanoDet NanoDet 介绍 可以参考这个博客&#xff1a;NanoDet&#xff1a;这是个小于4M超轻量目标检测模型 源码 …...

编程日记 2024/3/18 20:08:00

突破编程_C++_C++11新特性（unordered_multimap）

1 概述 std::unordered_multimap 是一个哈希表实现的无序容器&#xff0c;它存储的元素是键值对&#xff0c;并且允许键的重复。这意味着同一个键可以关联多个值。在 std::unordered_multimap 中&#xff0c;元素的插入顺序是不确定的&#xff0c;并且不会因为元素的插入、删除…...

编程日记 2024/3/18 20:06:59

15.WEB渗透测试--Kali Linux（三）

免责声明&#xff1a;内容仅供学习参考&#xff0c;请合法利用知识&#xff0c;禁止进行违法犯罪活动&#xff01; 内容参考于&#xff1a; 易锦网校会员专享课 上一个内容&#xff1a;14.WEB渗透测试--Kali Linux&#xff08;二&#xff09;-CSDN博客 Kali工具使用 3389远…...

编程日记 2024/3/18 20:05:58

Android-Framework pm list packages和pm install返回指定应用信息

一、环境 高通 Android 13 注&#xff1a;Android10 和Android13有些差异&#xff0c;代码位置不变&#xff0c;参照修改即可 二、pm简单介绍 pm工具为包管理&#xff08;package manager&#xff09;的简称 可以使用pm工具来执行应用的安装和查询应用宝的信息、系统权限、…...

编程日记 2024/3/18 20:03:56

CSS

什么是CSS&#xff1f; CSS是一门语言&#xff0c;用于控制网页表现 CSS&#xff08;Cascading Style Sheet&#xff09;&#xff1a;层叠样式表 W3C标准&#xff1a;网页主要由三部分组成 结构&#xff1a;HTML表现&#xff1a;CSS行为&#xff1a;JavaScript CSS导入方式…...

编程日记 2024/3/18 20:02:55

算法详解——选择排序和冒泡排序

一、选择排序 选择排序算法的执行过程是这样的&#xff1a;首先&#xff0c;算法遍历整个列表以确定最小的元素&#xff0c;接着&#xff0c;这个最小的元素被置换到列表的开头&#xff0c;确保它被放置在其应有的有序位置上。接下来&#xff0c;从列表的第二个元素开始&#x…...

编程日记 2024/3/18 19:56:50