蓝桥杯-带分数
法一
/*
再每一个a里去找c,他们共用一个st数组,可以解决重复出现数字
通过ac确定b,b不能出现<=0 b出现的数不能和ac重复*/import java.util.Scanner;public class Main {static int n,res;static boolean[] st = new boolean[15];static boolean[] backup = new boolean[15];static int[] data = new int[15];public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();dfs_a(1,0);System.out.println(res);}public static void dfs_a(int u,int a){if (a > n) return;//每一个a里去找不出现a中数字的c的全排列if (a > 0)dfs_c(u,a,0);for(int i = 1;i <= 9;i++){if (!st[i]){st[i] = true;dfs_a(u + 1,a * 10 + i);st[i] = false;}}}public static void dfs_c(int u,int a,int c){if (u == 9) return;if (c > 0)//通过ac确定bif (check(a,c)) res++;for(int i = 1;i <= 9;i++){if (!st[i]){st[i] = true;dfs_c(u + 1,a,c * 10 + i);st[i] = false;}}}public static boolean check(int a,int c){//n 和 c 可能会溢出long b = n * (long)c - a * c;if (b <= 0) return false;backup = st.clone();while (b > 0){//b的每一位不能再之前出现过,并且不能等于0int ge = (int)b % 10;b /= 10;if (backup[ge] || ge == 0) return false;backup[ge] = true; //记得出现出的数字也要标记一下}for(int i = 1;i <= 9;i++){if (!backup[i]) return false;}return true;}
}
法二
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;public class Main {static int n;// 目标数static int[] a = new int[10];// 全排列数组static boolean visi[] = new boolean[10]; // 放入数组就进行记录,避免重复使用static int ans = 0;// 统计public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();dfs(1);System.out.println(ans);}//枚举全排列public static void dfs(int u){if(u == 10){check();return;}for (int i = 1; i <= 9; i++){if(!visi[i]){visi[i] = true;a[u] = i;dfs(u + 1);// 回溯visi[i] = false;}}}//切割成三份是否满足题目给定式子public static void check(){for(int i = 1 ; i <= 7;i++){//a最多可以取七位,取前七位即可,全排列有对称关系int num1 = Test(1, i);//枚举num1所有可能得长度//num1再继续加下面num2与num3也是超标已经超过了N,没有必要再继续if(num1 >= n)continue;for(int j = i + 1 ; j <= 8;j++){int num2 = Test(i + 1,j);//分子数int num3 = Test(j + 1, 9);//分母数if(num2 % num3 == 0 && num1 + num2 / num3 == n){//进行判断ans++;}}}}public static int Test(int start,int end){int number1 = 0;for (int i = start; i <= end; i++){number1 = number1 * 10 + a[i];}return number1;}
}相关文章:

蓝桥杯-带分数
法一 /* 再每一个a里去找c,他们共用一个st数组,可以解决重复出现数字 通过ac确定b,b不能出现<0 b出现的数不能和ac重复*/import java.util.Scanner;public class Main {static int n,res;static boolean[] st new boolean[15];static boolean[] backup new boolean[15];…...
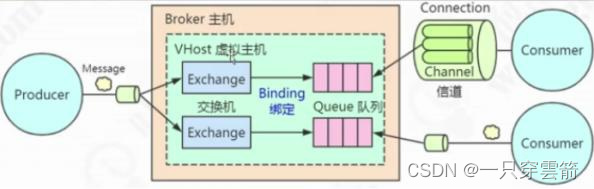
消息队列面试题
目录 1. 为什么使用消息队列 2. 消息队列的缺点 3. 消息队列如何选型? 4. 如何保证消息队列是高可用的 5. 如何保证消息不被重复消费(见第二条) 6. 如何保证消息的可靠性传输? 7. 如何保证消息的顺序性(即消息幂…...

Android和IOS应用开发-Flutter 应用中实现记录和使用全局状态的几种方法
文章目录 在Flutter中记录和使用全局状态使用 Provider步骤1步骤2步骤3 使用 BLoC步骤1步骤2步骤3 使用 GetX:步骤1步骤2步骤3 在Flutter中记录和使用全局状态 在 Flutter 应用中,您可以使用以下几种方法来实现记录和使用全局状态,并在整个应…...

若依 ruoyi-cloud [网关异常处理]请求路径:/system/user/getInfo,异常信息:404
这里遇到的情况是因为nacos中的配置文件与项目启动时的编码不一样,若配置文件中有中文注释,那么用idea启动项目的时候,在参数中加上 -Dfile.encodingutf-8 ,保持编码一致,(用中文注释的配置文件,…...
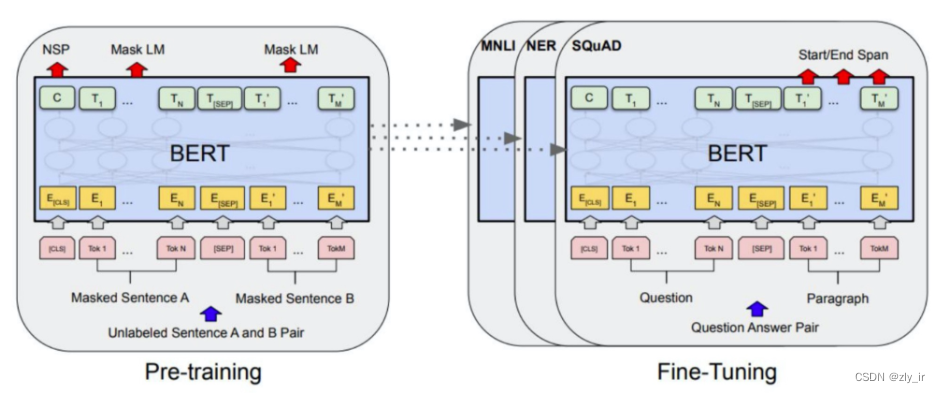
自然语言处理里预训练模型——BERT
BERT,全称Bidirectional Encoder Representation from Transformers,是google在2018年提出的一个预训练语言模型,它的推出,一举刷新了当年多项NLP任务值的新高。前期我在零、自然语言处理开篇-CSDN博客 的符号向量化一文中简单介绍…...

2024年信息技术与计算机工程国际学术会议(ICITCEI 2024)
2024年信息技术与计算机工程国际学术会议(ICITCEI 2024) 2024 International Conference on Information Technology and Computer Engineering ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 大会主题: 信息系统和技术…...

渗透测试修复笔记 - 02 Docker Remote API漏洞
需要保持 Docker 服务运行并且不希望影响其他使用 Docker 部署的服务,同时需要禁止外网访问特定的 Docker API 端口(2375):通过一下命令来看漏洞 docker -H tcp://ip地址:2375 images修改Docker配置以限制访问 修改daemon.json配…...
)
Spring(创建对象的方式3个)
3、Spring IOC创建对象方式一: 01、使用无参构造方法 //id:唯一标识 class:当前创建的对象的全局限定名 <bean id"us1" class"com.msb.pojo.User"/> 02、使用有参构造 <bean id"us2&…...
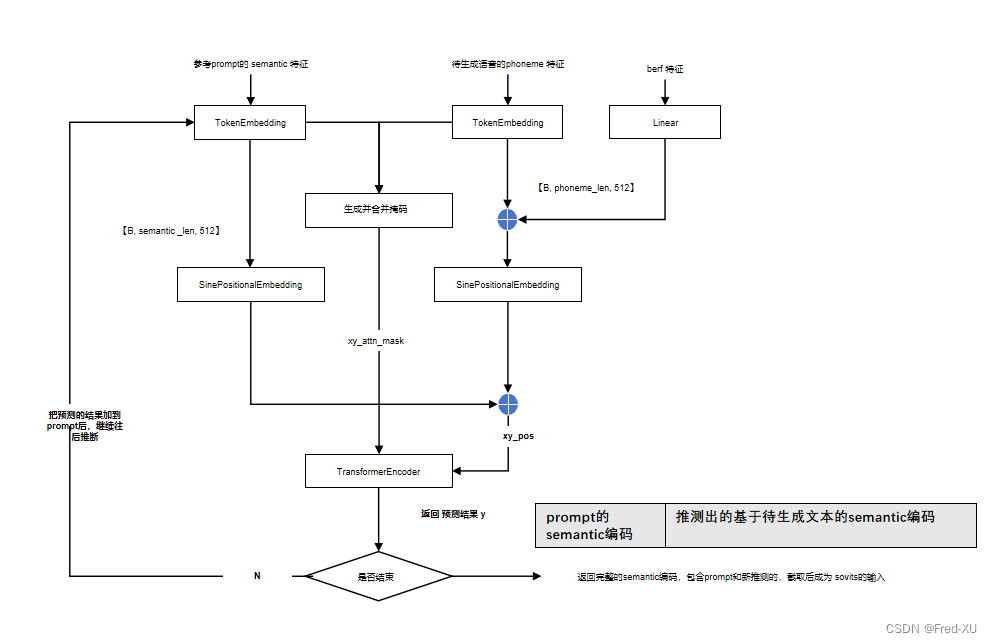
【GPT-SOVITS-02】GPT模块解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...
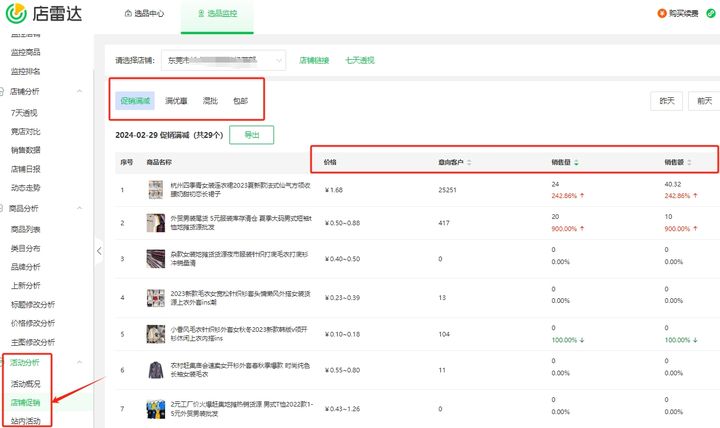
6个选品建议,改善你的亚马逊现状。
一、市场热点与需求调研 深入研究当前市场趋势,了解消费者需求的变化。使用亚马逊的销售数据、评价、问答等功能,以及第三方市场研究工具,比如店雷达,分析潜在热销产品的特点。注意季节性需求,提前布局相关选品&#…...

SQL中的SYSDATE函数
前言 在SQL语言中,SYSDATE 是一个非常实用且常见的系统内置函数,尤其在Oracle和MySQL数据库中广泛使用。它主要用来获取服务器当前的日期和时间,这对于进行实时数据记录、审计跟踪、有效期计算等场景特别有用。本文将详细解析SYSDATE函数的使…...

Rust的async和await支持多线程运行吗?
Rust的async和await的异步机制并不是仅在单线程下实现的,它们可以在多线程环境中工作,从而利用多核CPU的并行计算优势。然而,异步编程的主要目标之一是避免不必要的线程切换开销,因此,在单线程上下文中,asy…...

P2676 [USACO07DEC] Bookshelf B
[USACO07DEC] Bookshelf B 题目描述 Farmer John 最近为奶牛们的图书馆添置了一个巨大的书架,尽管它是如此的大,但它还是几乎瞬间就被各种各样的书塞满了。现在,只有书架的顶上还留有一点空间。 所有 N ( 1 ≤ N ≤ 20 , 000 ) N(1 \le N…...
)
【数学】第十三届蓝桥杯省赛C++ A组/研究生组《爬树的甲壳虫》(C++)
【题目描述】 有一只甲壳虫想要爬上一棵高度为 n 的树,它一开始位于树根,高度为 0,当它尝试从高度 i−1 爬到高度为 i 的位置时有 Pi 的概率会掉回树根,求它从树根爬到树顶时,经过的时间的期望值是多少。 【输入格式…...

Java毕业设计 基于springboot vue招聘网站 招聘系统
Java毕业设计 基于springboot vue招聘网站 招聘系统 springboot vue招聘网站 招聘系统 功能介绍 用户:登录 个人信息 简历信息 查看招聘信息 企业:登录 企业信息管理 发布招聘信息 职位招聘信息管理 简历信息管理 管理员:注册 登录 管理员…...

Leetcode 1. 两数之和
心路历程: 很简单的题,双层暴力就可以,用双指针的话快一点。暴力时间复杂度O( n 2 n^2 n2),双指针时间复杂度O(nlogn) O(n) O(n) O(nlogn)。 注意的点: 1、题目需要返回原数组的索引,所以排序后还需要…...
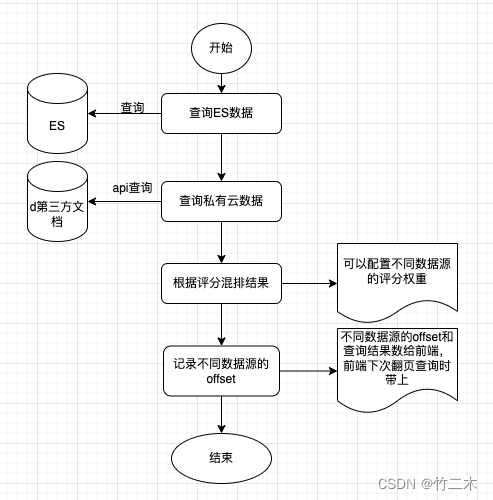
【elasticsearch实战】从零开始设计全站搜索引擎
业务需求 最近需要一个全站搜索的功能,我们的站点的特点是数据多源,即有我们本地数据库,也包含了第三方数据源,我们的数据类型除了网页,还包括了各种类型的文档,例如:doc、pdf、excel、ppt等格…...

基于tcp协议的网络通信(基础echo版.多进程版,多线程版,线程池版),telnet命令
目录 基础版 思路 辅助函数 服务端 代码 运行情况 -- telnet ip 端口号 传输的数据为什么没有转换格式 客户端 思路 代码 多进程版 引入 问题 解决 注意点 服务端 代码 运行情况 进程池版(简单介绍) 多线程版 引入 问题解决 注意点 服务端 代码 …...

Ubuntu20系统安装完后没有WIFI
Ubuntu20系统安装完后没有WIFI 查看后发现是缺少网卡,经过查询之后,发现是HRex39/rtl8852be 然后查询了Kernel版本 Check the Kernel Version in Linux $ uname -srm Linux 5.15.0-67-generic x86_64然后进行下载安装 Build(for kernel < 5.18) …...

计算机视觉——目标检测(R-CNN、Fast R-CNN、Faster R-CNN )
前言、相关知识 1.闭集和开集 开集:识别训练集不存在的样本类别。闭集:识别训练集已知的样本类别。 2.多模态信息融合 文本和图像,文本的语义信息映射成词向量,形成词典,嵌入到n维空间。 图片内容信息提取特征&…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
