考研机试题
目录
- 头文件与STL
- 动态规划
- 最大数组子串和
- 最长公共子序列
- 最长连续公共子串
- 最长递增子序列
- 最大上升子序列和
- 0-1背包
- 多重背包
- 多重背包问题 I
- 整数拆分
- 最小邮票
- 最大子矩阵
- 数学问题
- 朴素法筛素数
- 线性筛素数
- 快速幂
- 石子合并
- 锯木棍
- 并查集
- Dijkstra单源最短路
- Python进制转换(整数无限大)
- 全排列
- 神奇的口袋
- 全排列II
- 放苹果
- 求第k小
- 八皇后问题
- 哈夫曼编码
- KMP算法
- 遍历建立二叉树
头文件与STL
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;vector.insert(vector.begin(),2,99)//在头部插入2个99
vector.erase(vector.begin() + 5, vector.end()) //删除第5个以后的元素map<string,int>
map.insert(pair<string, int>())
map.count() //0或1
map.earse() //删除string s;
s.find()
s.substr(int start,int length) //切割子串
//输入含空格字符串
getline(cin,s); //优先队列
priority_queue<int,vecotr<int>,greater<int>>; //less是降序python输入
import sys
for line in sys.stdin:arr = line.split()
//拼接列表' '.join(list)a = int(arr[0])动态规划
最大数组子串和
dp[i]其实代表的是以i结尾的最大子串和
for(int i=0;i<n;i++){cin>>a[i];// 需要额外的ans存储max,因为是子串dp[i+1]=max(dp[i]+a[i],a[i]);ans=max(dp[i+1],ans);
}
最长公共子序列
动态规划
for(int i=1;i<=s1.size();i++){for(int j=1;j<=s2.size();j++){if(s1[i-1]==s2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}
}
最长连续公共子串
//t存储公共子串在s1中的末尾位置
int t=0;
//最大长度,要额外的maxLen存储max,因为是子串
int maxLen=0;
for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s1[i-1]==s2[j-1]){dp[i][j]=dp[i-1][j-1]+1;// =号确保 如果不唯一,则输出s1中的最后一个。if(dp[i][j]>=maxLen){maxLen=dp[i][j];//存储公共子串在s1中的末尾位置,可以输出子串t=i-1;}} }
}
最长递增子序列
https://www.nowcoder.com/practice/cf209ca9ac994015b8caf5bf2cae5c98?tpId=40&tags=&title=&difficulty=0&judgeStatus=0&rp=1&sourceUrl=
dp[i]只代表以i结尾的最长递增子序列数
for(int i=0;i<n;i++){//初始化:最长为本身 1dp[i]=1;for(int j=0;j<i;j++){//dp[i]代表以i结尾的最长递增子序列数if(a[i]>a[j])dp[i]=max(dp[j]+1,dp[i]);ans=max(dp[i],ans);}
}
最大上升子序列和
和上述最长递增子序列思路一致,不过dp[i]代表以i结尾的最长递增子序列的和,用ans存储结果
0-1背包
int dp[1001][1001];//代表前i个物体,背包为j的最大价值
int n,bag;
int v[10001],w[10001];
cin>>n>>bag;
for(int i=1;i<=n;i++){cin>>v[i]>>w[i];
}
dp[0][0]=0;
for(int i=1;i<=n;i++){for(int j=1;j<=bag;j++){if(j>=v[i]){dp[i][j]=max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);}else{dp[i][j]=dp[i-1][j];}}
}
cout<<dp[n][bag];
多重背包
每种物品无限件
for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}
}
多重背包问题 I
第 i 种物品最多有 si件,
//将 si拆成多个物品,即01背包while(s--)
{a[++t]=v;b[t]=w;
}//死拆,把多重背包拆成01背包
整数拆分
一个整数总可以拆分为2的幂的和
//奇数
if(i%2)dp[i]=dp[i-1];
//偶数 ?没想明白***
else dp[i]=(dp[i-1]+dp[i/2])%1000000000;
最小邮票
dp[0][0]=0;
for(int i=1;i<=m;i++){//代表集不齐dp[0][i]=1e9;
}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j-a[i]>=0)dp[i][j]=min(dp[i-1][j-a[i]]+1,dp[i-1][j]);elsedp[i][j]=dp[i-1][j];}
}
最大子矩阵
子矩阵的和:pivot - dp[k-1][j] - dp[i][q-1] + dp[k-1][q-1]
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cin >> matrix[i][j];//计算机前缀和dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + matrix[i][j];}}int ans = INT_MIN;//记录最大子矩阵位置int x1,x2,y1,y2;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {int pivot = dp[i][j];for (int k = 1; k <= i; k++) {for (int q = 1; q <= j; q++) {if((pivot - dp[k-1][j] - dp[i][q-1] + dp[k-1][q-1])>ans){ans = max(ans, pivot - dp[k-1][j] - dp[i][q-1] + dp[k-1][q-1]);x1=k;x2=i;y1=q;y2=j;}}}}}cout << ans<<endl;cout<<x1<<y1<<" "<<x2<<y2<<endl;
数学问题
朴素法筛素数
求n以内的所有素数,时间O(nlog(logn))【不是最优:例如14会被2和7筛重复2次】
void get_primes(int n){for(int i=2;i<n;i++){//i被筛了,直接跳过if(st[i]) continue;//i是素数,添加进数组,并筛掉与i成倍数的非素数else {primes[cnt ++ ] = i;for(int j=2*i;j<=n;j+=i){//j一定不是素数st[j]=true;}}}
}
线性筛素数
时间O(n),解决重复筛
for(int i=2;i<=n;i++){//i没被筛,加入if(!st[i]) primes[prime_count++]=i;for(int j=0;j<prime_count;++j){if(prime[j]*i>n) break;//翻倍,一个数 * 素数一定为合数 st[primes[j]*i]=true;//退出循环,避免之后重复进行筛选if(i%primes[j]==0) break;}
}
快速幂
int qmi(int a,int b, int p){if(b==0)return 1 ; int k = qmi(a,b/2,p)%p;// k*k可能会超过int if(b%2==0)return (1LL*k*k) %p;else return ((1LL*k*k)%p*a)%p;}
石子合并
贪心:只能合并相邻的最小的两堆
int n;int min_idx=0;int min_sum=1e7;
// 边界处理ve.push_back(1e7);int ans=0;cin>>n;for(int i=1;i<=n;i++){int x;cin>>x;ve.push_back(x);if(min_sum>ve[i]+ve[i-1]){min_sum=ve[i]+ve[i-1];min_idx=i;}}while(ve.size()>2){ans += min_sum;ve[min_idx]=ve[min_idx]+ve[min_idx-1];ve.erase(ve.begin()+min_idx-1);min_sum=1e7;
// min_idx=0;if(ve.size()<=2) break; for(int i=1;i<ve.size();i++){if(min_sum>ve[i]+ve[i-1]){min_sum=ve[i]+ve[i-1];min_idx=i;}}}cout<<ans<<endl;锯木棍
贪心-思想是WPL最小带权路径,永远合并最小的两个
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
//自定义比较结构体
struct cmp{//函数重载 注意两个括号!!!bool operator()(int a,int b){//稳定if(a==b) return false;else return a>b;}
};int main(int argc, char** argv) {//priority_queue<int,vector<int>,greater<int>> que;priority_queue<int,vector<int>,cmp> que;int n,l;cin>>n>>l;int tmp;int ans=0;while(n--){cin>>tmp;que.push(tmp);} while(que.size()!=1){int a=que.top();que.pop();int b=que.top();que.pop();que.push(a+b);ans=ans+a+b;}cout<<ans; return 0;
}
并查集
int Find(int a){int x=a;while(s[x]>0){x=s[x];}return x;
}
void Union(int a,int b){root1=Find(a);root2=Find(b);if(root2==root1)return ;else{s[root2]=root1;}}
Dijkstra单源最短路
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i ++ ){int t = -1; // 在还未确定最短路的点中,确定一个最短的点for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;// 用t更新其他点的距离for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];}
Python进制转换(整数无限大)
import sysfor line in sys.stdin:a = line.split()a=int(a[0])b=bin(a)s=(b[2:][::-1])print(int(s,2))全排列
回溯法
void dfs(int k){if(k==n+1){for(int i=1;i<=n;i++){cout<<arr[i]<<' ';}cout<<'\n';return ;}for(int i=1;i<=n;i++){//还没访问的数if(!st[i]){st[i]=true;// 存储第k个数arr[k]=i;dfs(k+1);// 恢复-现场st[i]=false;}}
}
int main() { cin>>n;dfs(1);}神奇的口袋
有一个神奇的口袋,总容积是40,有n个物品,体积为Vi,装满40有多少种装法
void dfs(int u,int j){if(u==40){ans++; }else{//从j开始,前面用过的舍弃掉,防止重复for(int i=j;i<n;i++){if(!st[i]){st[i]=true;dfs(u+v[i],i);st[i]=false;}}}
}
全排列II
带有重复元素的全排列
void dfs(int k){if(k==n+1){for(int i=1;i<=n;i++){cout<<arr[i]<<' ';}cout<<'\n';return ;}for(int i=1;i<=n;i++){//还没访问的数if(!st[i]){st[i]=true;// 存储第k个数arr[k]=i;dfs(k+1);// 恢复-现场st[i]=false;//***当与后一个元素重复时,跳过不排列,且这一步要在恢复现场之后做while(s[i+1]==s[i])i++;}}
}
int main() { cin>>n;//使重复的元素排在一起sort(a,a+n);dfs(1);}
放苹果
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
//处理边界
for(int i=0;i<=m;i++){//为0的可以不用处理,数组默认为0//1个盘子的dp[i][1]=1;
}
for(int i=0;i<=n;i++){//0个苹果的dp[0][i]=1;
}for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){//如果盘子多,多余的用不到的盘子都是没用的if(j>i){dp[i][j]=dp[i][i];}//如果苹果多,dp[i][j]等于 有空盘子的(挑一个盘子为空)+没有空盘子(每个盘子初始都放一个苹果)的状态else{dp[i][j]=dp[i][j-1]+dp[i-j][j];}}
}
求第k小
使用快排划分的思想
#include <iostream>
#include <algorithm>
/**求第k小 */
using namespace std;
int n;
int a[10001];
int k;
void partition(int start,int end) {int pivot=a[start];int l=start;int r=end;while(l<r) {while(a[l]<pivot) {l++;}while(a[r]>pivot) {r--;}swap(a[l],a[r]);}a[l]=pivot;if(l==k-1) {cout<<a[l];return ;}else if(l<k){partition(l+1,end);}else{partiton(start,l);}
}int main(int argc, char** argv) {cin>>n;cin>>k;for(int i=0; i<n; i++) {cin>>a[i];}partition(0,n-1);return 0;
}
八皇后问题
哈夫曼编码
priority_queue<int,vector<int>,greater<int> q;
int alpha[26];
//去最小的两个
KMP算法
//字符串下标都从0开始
void getNextTable(int m){int j=0;next[0]=-1;int i=-1;while(j<m){if(i==-1 || pattern[j]==pattern[i]){i++;j++;next[j]=i;}else{i=next[i];}}return ;
}int kMP(string a,string b){int i=0,j=0;while(i<n&&j<m){if(j==-1 || s[i]==pattern[j]){i++;j++;}else{j=next[j];}}if(j==m){return i-j+1;}else{//匹配失败return -1;}
}
遍历建立二叉树
TNode(char c):data©,left(nullptr),right(nullptr){};
using TreeNode = struct TNode{char data;struct TNode* left;struct TNode* right;TNode(char c):data(c),left(nullptr),right(nullptr){};
};TreeNode* Build(TreeNode* root,char c){if(c=='#')return NULL;
// C style:(TreeNode*)malloc(sizeof(TreeNode))root=new TNode(c);char c1=s[cnt++];root->left=Build(root->left,c1);char c2=s[cnt++];root->right=Build(root->right,c2);return root;
}void Inorder(TreeNode* root){if(root->left)Inorder(root->left);cout<<root->data<<endl;if(root->right)Inorder(root->right);}
void postOrder(TreeNode* root){}int main(int argc, char** argv) {TreeNode* T=NULL;T=Build(T,s[cnt++]);Inorder(T);return 0;
}
相关文章:

考研机试题
目录 头文件与STL动态规划最大数组子串和最长公共子序列最长连续公共子串最长递增子序列最大上升子序列和0-1背包多重背包多重背包问题 I整数拆分最小邮票最大子矩阵 数学问题朴素法筛素数线性筛素数快速幂 石子合并锯木棍并查集Dijkstra单源最短路Python进制转换(整数无限大)全…...
)
Java基础知识总结(6)
String类中常用的类方法: 方法名称描述format(String format, Object... args)使用指定的格式字符串和参数返回一个格式化字符串。 format - 格式字符串 args - 格式字符串中由格式说明符引用的参数。如果还有格式说明符以外的参数,则忽略这些额外的参数…...

JAVA基础—关于Java的反射机制
1. Java的反射机制是什么? 反射(reflection) 当我们谈及反射,可以将其比作正在照镜子的行为。就像你可以在禁止中看到自己的反射一样,程序在运行时可以检查自身的机构和行为。这意味这程序可以动态地了解自己地组成部分,比如类、…...

Hive中的explode函数、posexplode函数与later view函数
1.概述 在离线数仓处理通过HQL业务数据时,经常会遇到行转列或者列转行之类的操作,就像concat_ws之类的函数被广泛使用,今天这个也是经常要使用的拓展方法。 2.explode函数 2.1 函数语法 -- explode(a) - separates the elements of array …...

北京市委统战部领导一行莅临百望云视察调研
“当今时代,数字技术、数字经济是世界科技革命和产业变革的先机,是新一轮国际竞争重点领域”。 为了解数字标杆企业的发展现状,促进新质生产力与实体产业的协同与赋能,近日,北京市委统战部非公经济处处长王雷、副处长徐…...

使用Python进行数据库连接与操作SQLite和MySQL【第144篇—SQLite和MySQL】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 使用Python进行数据库连接与操作:SQLite和MySQL 在现代应用程序开发中…...

How to manage Python environment based on virtualenv in Ubuntu 22.04
How to manage Python environment based on virtualenv in Ubuntu 安装使用创建环境激活环境安装软件包退出环境移除环境 安装 pip3 install virtualenv使用 创建环境 lwkqwfys:~$ mkdir ~/project/harbin lwkqwfys:~$ cd ~/project/harbin lwkqwfys:~/project/harbin$ vir…...
一款基于 SpringCloud 开发的AI聊天机器人系统,已对接GPT-4.0,非常强大
简介 一个基于SpringCloud的Chatgpt机器人,已对接GPT-3.5、GPT-4.0、百度文心一言、stable diffusion AI绘图、Midjourney绘图。用户可以在界面上与聊天机器人进行对话,聊天机器人会根据用户的输入自动生成回复。同时也支持画图,用户输入文本…...

C语言自定义库
编写 xx.c 和xx.h文件\将源代码编译为目标文件 gcc -c add.c sub.c 执行完毕后会生产add.o和sub.o文件静态库创建使用ar命令; ar -r libmymath.a add.o sub.o将库和main.c文件一起编译 gcc -o main main.c -lmymath -L./ 注意 上述书写格式不要错乱 -L 是指定文件路…...
)
目标检测常见数据集格式(YOLO、VOC、COCO)
目录 1.YOLO格式数据 1.1数据格式 1.2YOLO格式数据示例 1.3YOLO格式可视化 2.COCO数据格式 2.1数据格式 2.2COCO格式数据示例 2.3COCO格式可视化 3.VOC数据格式 3.1数据格式 3.2VOC格式数据示例 3.3COCO格式可视化 🍓🍓1.YOLO格式数据 &…...
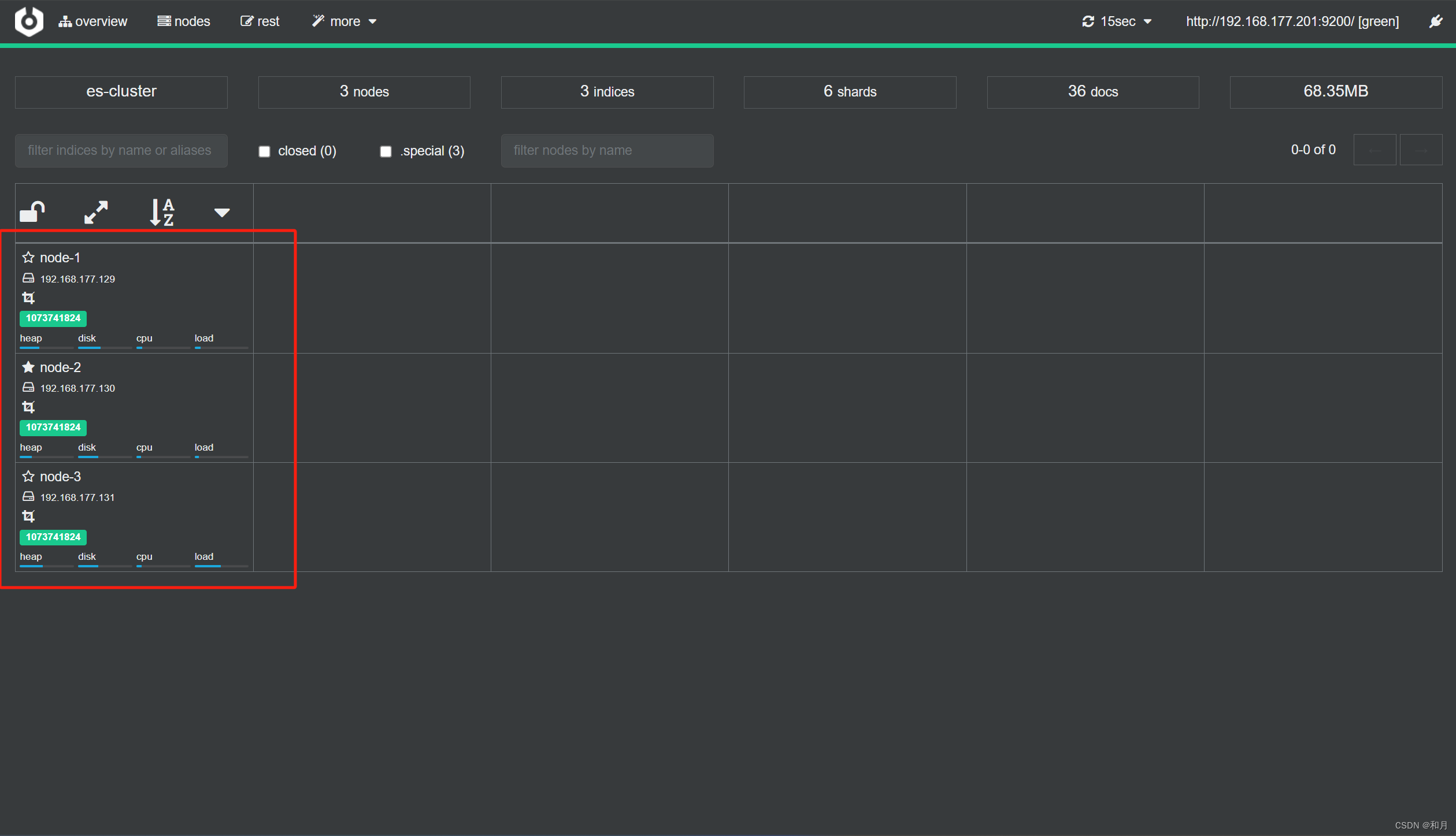
搭建 es 集群
一、VMware准备机器 首先准备三台机器 这里我直接使用 VMware 构建三个虚拟机 都是基于 CentOS7 然后创建新用户 部署 es 需要单独创建一个用户,我这里在构建虚拟机的时候直接创建好了 然后将安装包上传 可以使用 rz 命令上传,也可以使用工具上传 工…...

Android弹出通知
发现把Android通知渠道的重要性设置为最高时,当发送通知时,通知能直接弹出来显示,以前一直搞不明白为什么别的app的通知可以弹出来,我的不行,搞了半天原来是这个属性在作怪,示例如下: class Ma…...

如何用 UDP 实现可靠传输?并以LabVIEW为例进行说明
UDP(用户数据报协议)本身是一个无连接的、不可靠的传输协议,它不提供数据包的到达确认、排序保证或重传机制。因此,如果要在UDP上实现可靠传输,就需要在应用层引入额外的机制。以下是一些常见的方法: 确认和…...

【任职资格】某大型商业金融银行任职资格体系搭建项目纪实
【客户背景】某大型商业金融银行位于南方某省,成立于上个世纪九十年代,是一家具有独立法人资格的股份制商业银行,经过多年发展,下辖20多家分行,近200多个营业网点,并于21世纪初成功上市,规模不断…...

如何利用IP地址分析风险和保障网络安全
随着网络攻击的不断增加和演变,保障网络安全已经成为了企业和组织不可忽视的重要任务。在这样的背景下,利用IP地址分析风险和建立IP风险画像标签成为了一种有效的手段。本文将深入探讨IP风险画像标签的作用以及如何利用它来保障网络安全。 IP风险画像查…...

轧钢自动化中的智能仪器:监控、控制和优化新视角
摘要:轧钢自动化是现在及未来的发展趋势,而自动化的轧钢发展,更是离不开形形色色的智能仪器,本文来看看那些应用于轧钢生产中的测量仪。 关键词:智能仪器,在线测量仪,测径仪,测宽仪,测厚仪,测长仪,工业数据分析采集软件…...

第十四届蓝桥杯省赛C++B组题解
考点 暴力枚举,搜索,数学,二分,前缀和,简单DP,优先队列,链表,LCA,树上差分 A 日期统计 暴力枚举: #include<bits/stdc.h> using namespace std; int …...

语音控制模块_雷龙发展
一 硬件原理 1,串口 uart串口控制模式,即异步传送收发器,通过其完成语音控制。 发送uart将来自cpu等控制设备的并行数据转换为串行形式,并将其串行发送到接收uart,接收uart然后将串行数据转换为接收数据接收设备的并行…...
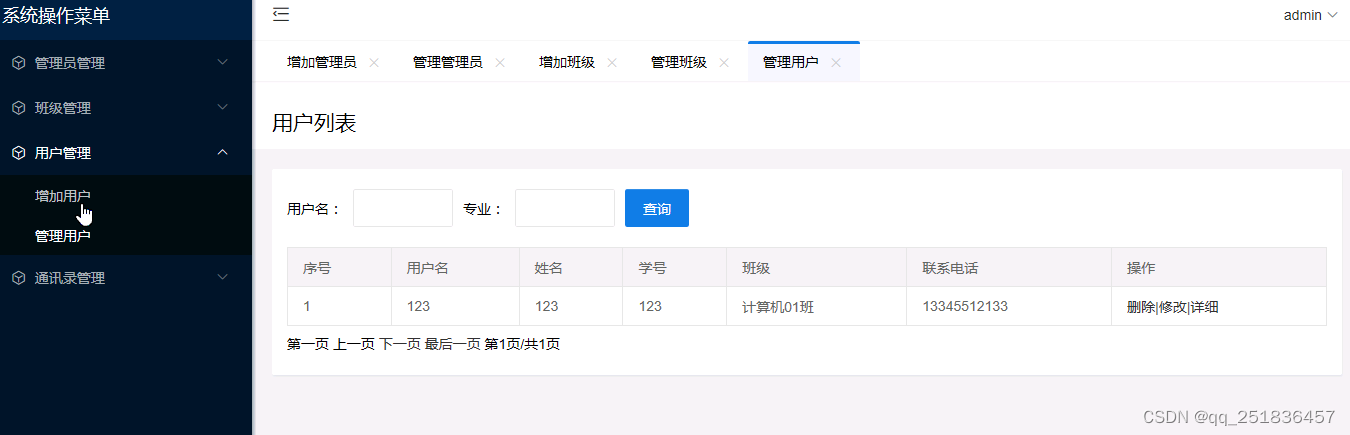
idea 开发serlvet班级通讯录管理系统idea开发mysql数据库web结构计算机java编程layUI框架开发
一、源码特点 idea开发 java servlet 班级通讯录管理系统是一套完善的web设计系统mysql数据库 系统采用serlvetdaobean mvc 模式开发,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 servlet 班…...

Python高级语法
Python高级语 1 列表推导式1.1 什么是列表推导式1.2 列表推导式的使用 2 字典推导式2.1 什么是字典推导式2.2 字典推导式的使用 3 元组推导式4 集合推导式5 三元表达式5.1 什么是三元表达式5.2 三元表达式的使用 1 列表推导式 1.1 什么是列表推导式 列表推导式的英文…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
