el-table按钮获取当前行元素
el-table按钮获取当前行元素
vue2
<el-table-column label="操作" width="240px"><template slot-scope="scope"><el-button size="mini" @click="toItem(scope.row)">用户详情</el-button><el-button size="mini" @click="toUpdate(scope.row)">编辑</el-button><el-button size="mini" type="danger" @click="handleDelete(scope.row)">删除</el-button></template></el-table-column>
el-table-column标签内部使用了 Vue 的插槽功能(slot),具体来说是使用了作用域插槽(scoped slot),通过 slot-scope=“scope” 来声明作用域,然后在插槽内容中可以使用 scope 对象来获取当前行的数据对象。
vue3
<template><div><el-table :data="tableData" style="border-radius: 5px;" :header-cell-style="{ 'text-align': 'center' }":cell-style="{ 'text-align': 'center' }"><el-table-column prop="date" label="Date" width="120" /><el-table-column prop="name" label="Name" width="120" /><el-table-column prop="address" label="Address" /><el-table-column label="操作" width="200px"><template #default="{ row }"><el-button type="danger" @click="handleDelete(row)">删除</el-button></template></el-table-column></el-table></div>
</template><script setup>
import { ref } from 'vue'const tableData = ref([])const handleDelete = (row) => {console.log(row)
}
</script>该组件中通过 Vue 的插槽功能和事件处理函数来获取和处理表格中每一行的数据对象。当用户点击编辑或删除按钮时,会触发相应的事件处理函数,并且可以在函数内部获取到相应行的数据对象进行进一步的处理。
相关文章:

el-table按钮获取当前行元素
el-table按钮获取当前行元素 vue2 <el-table-column label"操作" width"240px"><template slot-scope"scope"><el-button size"mini" click"toItem(scope.row)">用户详情</el-button><el-butto…...
MySQL数据导入的方式介绍
MySQL数据库中的数据导入是一个常见操作,它涉及将数据从外部源转移到MySQL数据库表中。在本教程中,我们将探讨几种常见的数据导入方式,包括它们的特点、使用场景以及简单的示例。 1. 命令行导入 使用MySQL命令行工具mysql是导入数据的…...

构建部署_Docker常用命令
构建部署_Docker常见命令 启动命令镜像命令容器命令 启动命令 启动docker:systemctl start docker 停止docker:systemctl stop docker 重启docker:systemctl restart docker 查看docker状态:systemctl status docker 开机启动&…...

Spring Boot Actuator介绍
大家在yaml中经常见到的这个配置 management: endpoints: web: exposure: #该配置线上需要去掉,会有未授权访问漏洞 include: "*" 他就是Actuator! 一、什么是 Actuator Spring Boot Actuator 模块提供了生产级别…...

数据库中DQL、DML、DDL、DCL的概念与区别
目录 DQL (Data Query Language) DML (Data Manipulation Language) DDL (Data Definition Language) DCL (Data Control Language) 数据库语言可以根据其功能被分为几个不同的类别:DQL(数据查询语言)、DML(数据操纵语言&…...

MacOS---设置Java环境变量
介绍 在MacOS系统配置Java环境变量。 操作步骤 第一步:打开.bash_profile文件 vim ~/.bash_profile第二步:添加或修改配置 如果是第一次配置需要添加配置如果是已经配置过想更换其他版本需要修改配置 在文件末尾添加或修改下面的配置 export JAVA…...
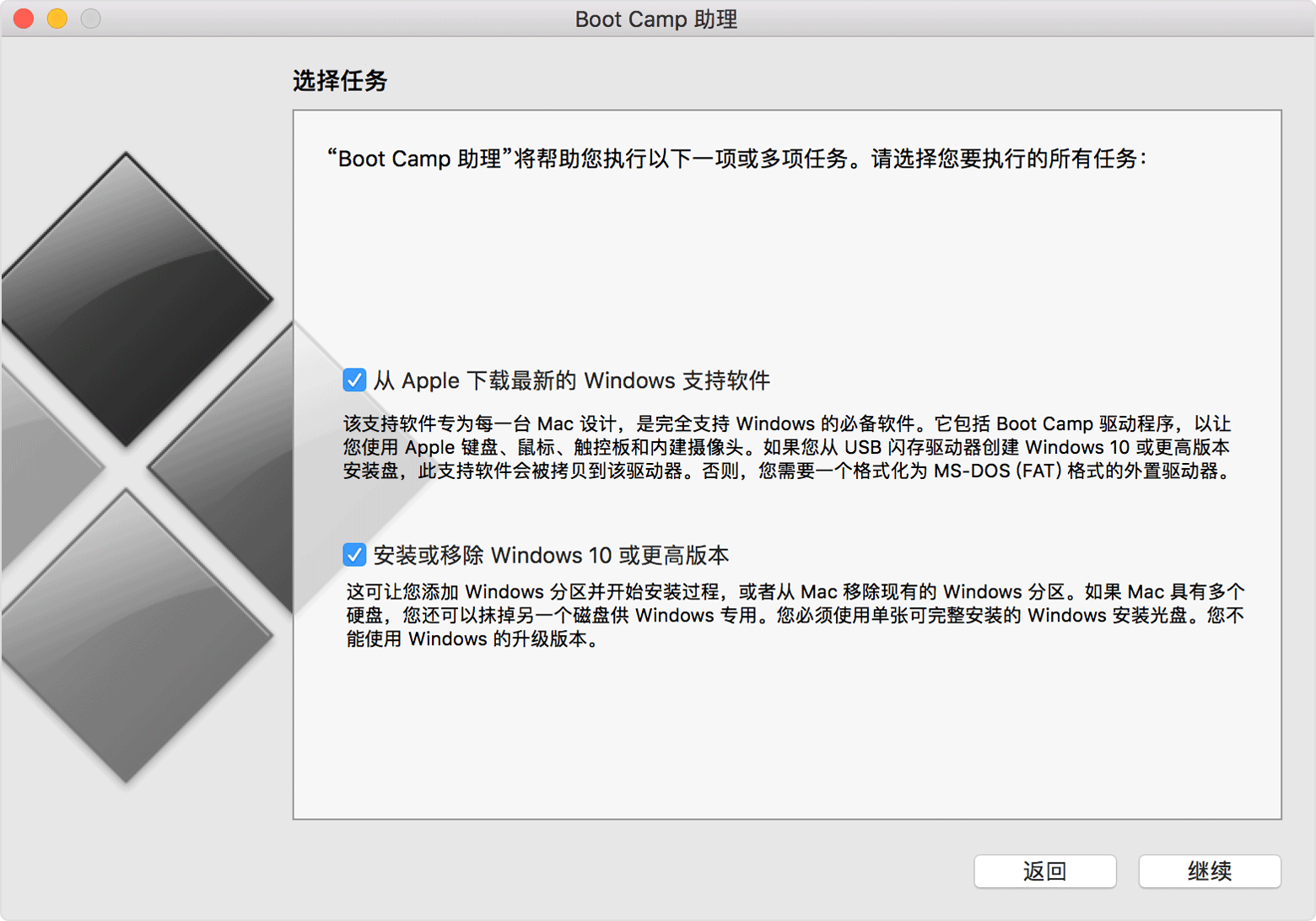
使用 Boot Camp 助理查明您的 Mac 需不需要 Windows 安装介质
使用 Boot Camp 助理查明您的 Mac 需不需要 Windows 安装介质 当前的 Mac 机型无需介质即可安装 Windows,也就是说,您不需要用到外置驱动器。较早的 Mac 机型需要用到 USB 驱动器或光盘驱动器。使用 Boot Camp 助理可查明您需要用到什么。 Boot Camp 助…...
)
KY105 整除问题(用Java实现)
描述 给定n,a求最大的k,使n!可以被a^k整除但不能被a^(k1)整除。 输入描述: 两个整数n(2<n<1000),a(2<a<1000) 输出描述: 一个整数. 示例1 输入: 6 10输出: 1代…...

C++ 接口的实现,及作用通俗理解方式
接口 C中的接口,一般就是指抽象类,是一种用来描述类对外提供的操作、方法或功能的集合——注意,一般只是描述(声明),而不对这些方法或功能进行定义实现,通常在类的继承或多态中作为基类使用&am…...
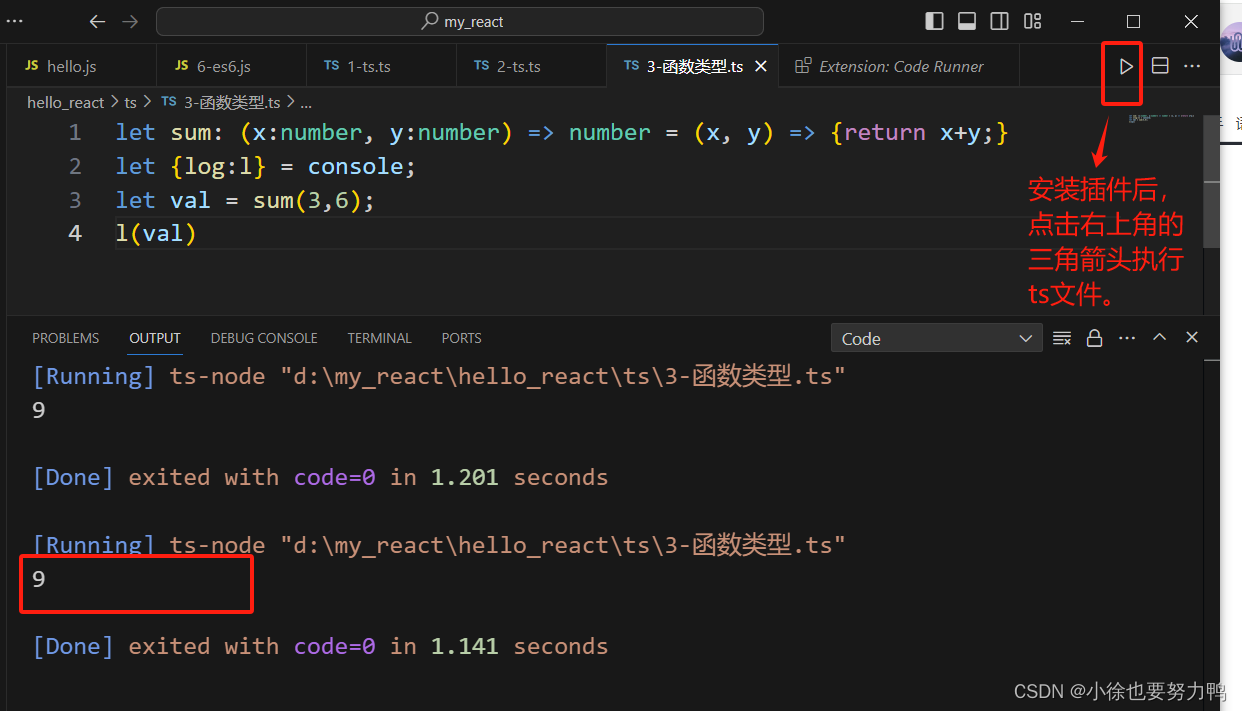
TypeScript:typescript的安装与运行
TypeScript:typescript的安装与运行 1 安装方式 -g全局安装TypeScript: npm install -g typescript2 运行方式 (1)ts编译成js,使用node命令运行js文件 打开vscode,进入ts文件所在目录下并打开终端term…...

【代码随想录Day27】
Day 27 回溯算法03 今日任务 组合总和 40.组合总和II131.分割回文串 代码实现 组合总和,直接套模板可解 public List<List<Integer>> combinationSum(int[] candidates, int target) {backtracking(candidates, target, 0);return result;}void back…...
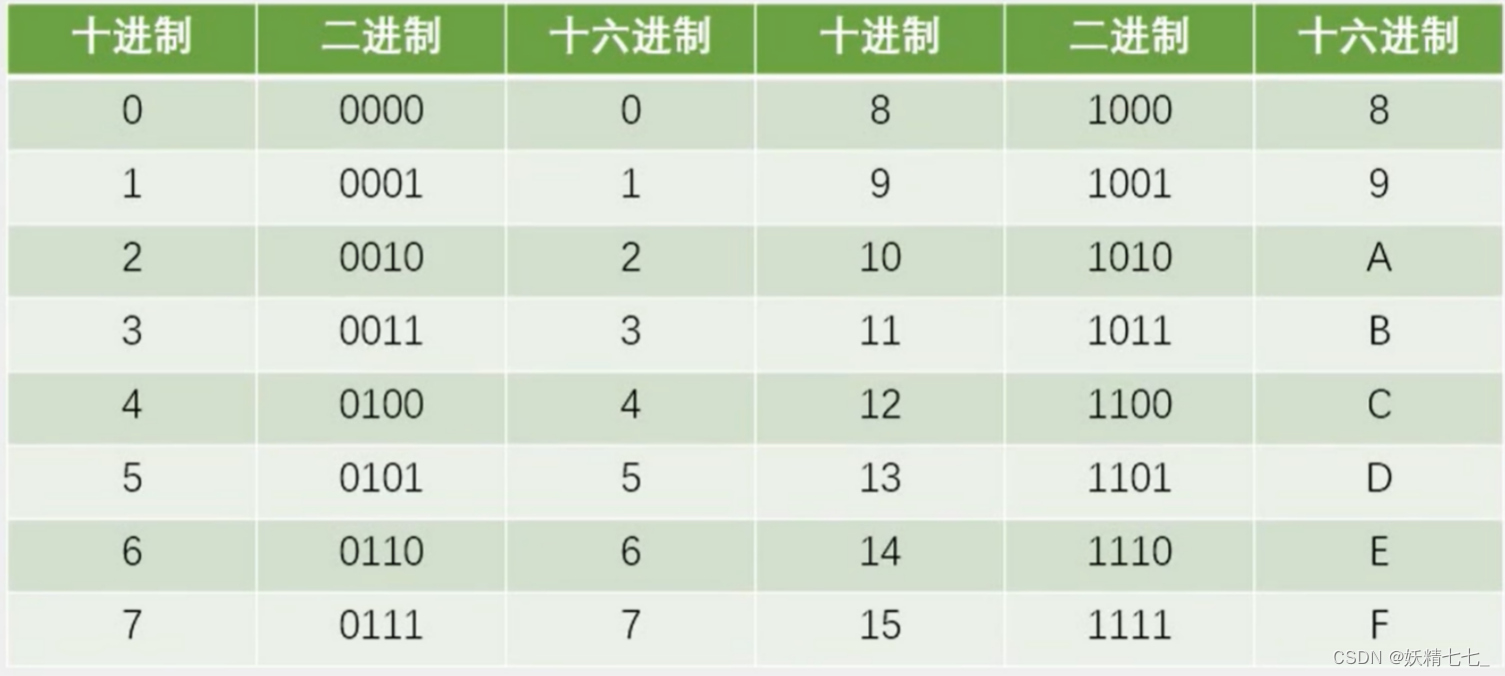
【一】【单片机】有关LED的实验
点亮一个LED灯 根据LED模块原理图,我们可以知道,通过控制P20、P21...P27这八个位置的高低电平,可以实现D1~D8八个LED灯的亮灭。VCC接的是高电平,如果P20接的是低电平,那么D1就可以亮。如果P20接的是高电平,…...

面试算法-49-缺失的第一个正数
题目 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出:3 解释:范围 [1,2] 中的数字都…...
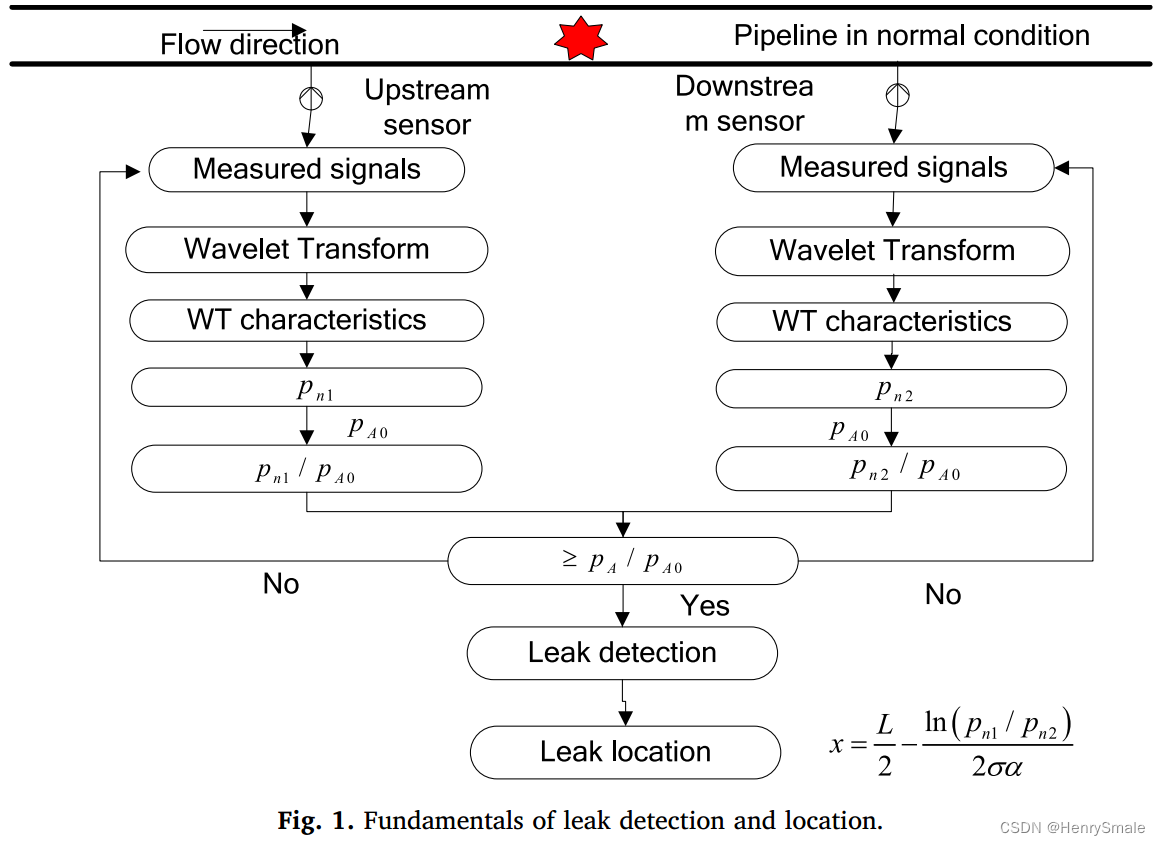
论文笔记:液体管道泄漏综合检测与定位模型
0 简介 An integrated detection and location model for leakages in liquid pipelines 1 摘要 许多液体,如水和油,都是通过管道运输的,在管道中可能发生泄漏,造成能源浪费、环境污染和对人类健康的威胁。本文描述了一种集成的…...

抖音视频批量提取软件|无水印视频下载
抖音视频批量提取软件,让您高效下载精彩内容! 您是否经常需要下载抖音视频,但传统的下载方式繁琐且低效?别担心,我们为您提供了一款强大而智能的抖音视频批量提取软件,让您轻松实现下载无水印的精彩内容&am…...

Linux docker1--环境及docker安装
一、基础环境要求 Docker分为ce版本(免费,试用7个月)和ee版本(收费)。 最低配置要求:64位操作系统,centOS 7及以上,内核版本不低于3.10 二、部署docker 1、查看服务的基础环境是否满…...
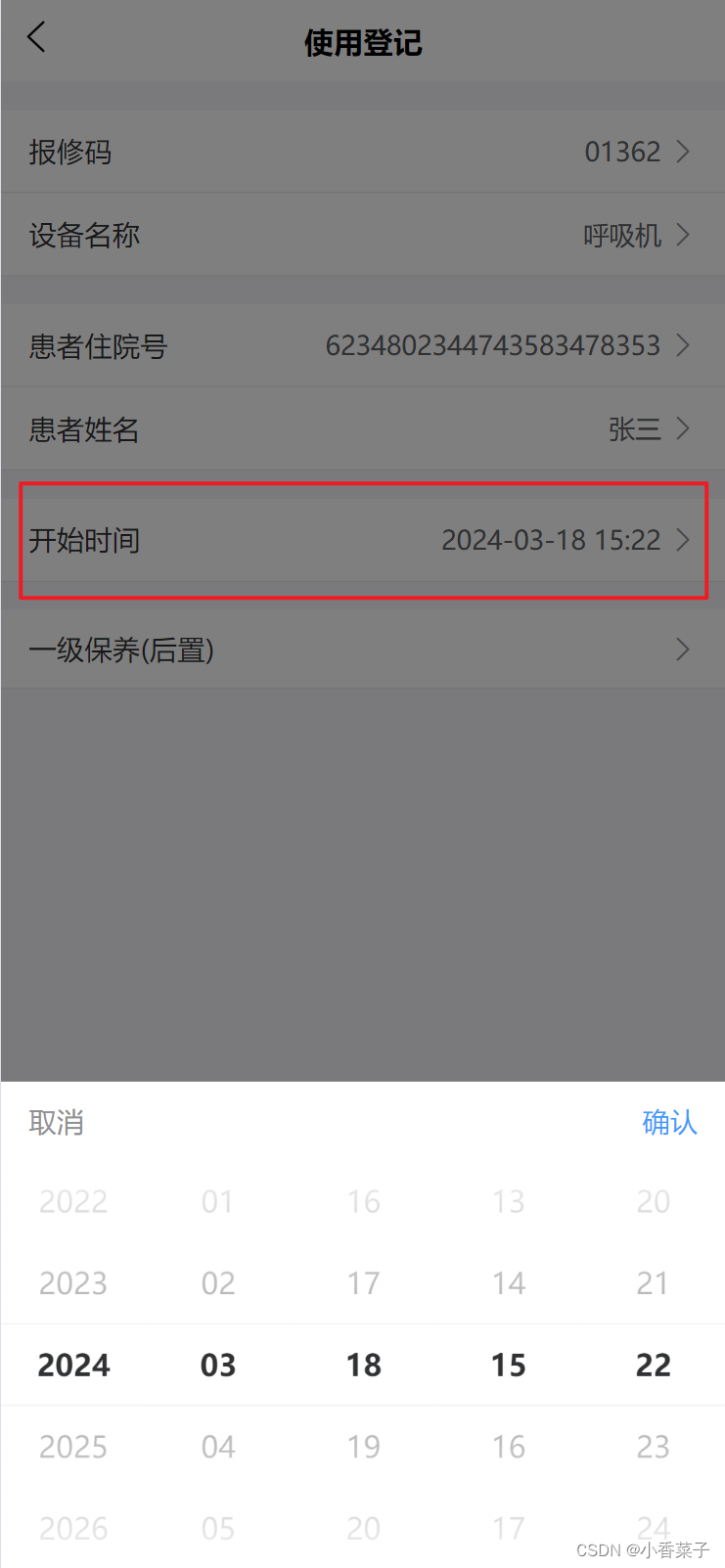
uniapp使用uview - DatetimePicker 时间选择器 /时间戳转化
uniapp使用uview - DatetimePicker 时间选择器 /时间戳转化时转换日期格式后页面仍显示时间戳 单元格内显示时间,点击可出现时间选择器切换时间 <u-cell :isLinktrue click"selectTime" title"开始时间" :value"startTime">…...

python实现websocket
WebSocket 是一种在单个 TCP 连接上进行全双工通信的协议。它允许客户端和服务器之间进行实时数据传输,而不是像 HTTP 协议那样,每次请求都需要建立新的连接。WebSocket 协议最初是由 HTML5 定义的,旨在提供一种更有效的替代方案,…...

ElasticSearch简介及常见用法
简介 Elasticsearch 是 Elastic Stack 核心的分布式搜索和分析引擎。 Logstash 和 Beats 有助于收集、聚合和丰富您的数据并将其存储在 Elasticsearch 中。 Kibana 使您能够以交互方式探索、可视化和分享对数据的见解,并管理和监控堆栈。 Elasticsearch 可以快速索…...

js iframe获取documen中的对象为空问题
原因其实是iframe加载是需要时间的,它还没加载完我就在js中直接获取对象了,所以获取为空 var idocument.getElementById("iframe"); i.onloadfunction(){console.log(i.contentDocument)console.log(i.contentWindow.document.getElementById…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
