连续纯合片段(runs of homozygosity, ROH)的原理
连续纯合片段(Runs of Homozygosity, ROH)的原理及其结果查看方式包含以下几个方面:
原理
-
定义和识别: ROH是指基因组中由相同祖先遗传下来的连续纯合等位基因组成的片段。它们可以通过比较个体基因组上的等位基因序列来识别。当一段DNA在某个个体中从其两个亲本那里继承了相同的等位基因时,这段DNA就形成了一个ROH。
-
产生机制: ROH的形成主要与近亲繁殖、种群规模减小(导致遗传漂变)、选择性压力等因素有关。近亲繁殖是最常见的原因,因为近亲繁殖增加了遗传物质相同的几率,从而在基因组中形成ROH。
-
遗传学意义: ROH在研究遗传疾病、种群遗传结构、人口历史等方面具有重要意义。长的ROH片段通常与近亲繁殖相关,而广泛分布的短ROH片段则可能指示古老的共同祖先或种群历史事件。
结果查看
-
基因组测序与分析软件: 通过高通量基因组测序技术,可以获取个体的完整基因组数据。随后,使用各种生物信息学软件和工具(如PLINK、GEMINI等)来分析这些数据,并识别出ROH。
-
结果呈现: 分析软件通常会提供ROH的位置、长度、所在染色体等详细信息。这些信息可以以表格的形式呈现,也可以通过图形界面展示,如基因组浏览器中的可视化图谱,展示ROH在某个个体基因组中的分布情况。
-
数据解读: 通过对ROH数据的解读,研究人员可以推断出个体的近亲繁殖程度、种群的遗传结构和历史。在医学研究中,通过关联分析,可以探索特定ROH区域与遗传疾病之间的联系。
应用
在遗传疾病的研究中,特别是对于那些受纯合有害变异影响的疾病,ROH的分析尤为重要。通过识别与疾病相关的ROH,科学家可以找到潜在的致病基因,为疾病的诊断和治疗提供线索。此外,ROH的研究还有助于理解人类历史和进化,以及保护生物多样性。
相关文章:
的原理)
连续纯合片段(runs of homozygosity, ROH)的原理
连续纯合片段(Runs of Homozygosity, ROH)的原理及其结果查看方式包含以下几个方面: 原理 定义和识别: ROH是指基因组中由相同祖先遗传下来的连续纯合等位基因组成的片段。它们可以通过比较个体基因组上的等位基因序列来识别。当…...
UCORE 清华大学os实验 lab0 环境配置
打卡 lab 0 : 环境配置 : 首先在ubt 上的环境,可以用虚拟机或者直接在windows 上面配置 然后需要很多工具 如 qemu gdb cmake git 就是中间犯了错误,误以为下载的安装包,一直解压不掉,结果用gpt 检查 结…...
linux 安装常用软件
文件传输工具 sudo yum install –y lrzsz vim编辑器 sudo yum install -y vimDNS 查询 sudo yum install bind-utils用法可以参考文章 《掌握 DNS 查询技巧,dig 命令基本用法》 net-tools包 yum install net-tools -y简单用法: # 查看端口占用情况…...

OpenMP使用教程:入门到精通
在并行编程的领域中,OpenMP无疑是一个强大而又便捷的工具,它让程序员能够以最少的努力实现程序的并行化。本文将详细介绍OpenMP的基本概念、环境配置、核心指令以及实际代码示例,旨在帮助读者从入门到精通OpenMP的使用。 什么是OpenMP&#…...
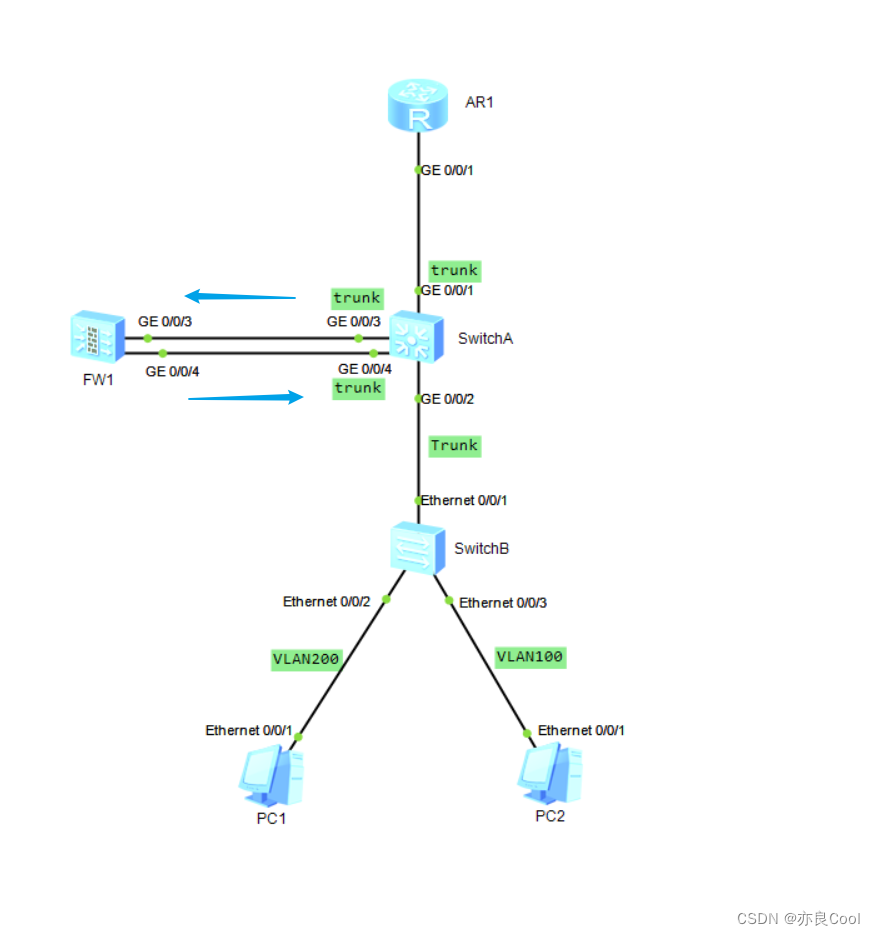
华为组网:核心交换机旁挂防火墙,基于ACL重定向配置实验
如图所示,由于业务需要,用户有访问Internet的需求。 用户通过接入层交换机SwitchB和核心层交换机SwitchA以及接入网关Router与Internet进行通信。为了保证数据和网络的安全性,用户希望保证Internet到服务器全部流量的安全性,配置重…...

HarmonyOS NEXT应用开发—投票动效实现案例
介绍 本示例介绍使用绘制组件中的Polygon组件配合使用显式动画以及borderRadius实现投票pk组件。 效果预览图 使用说明 加载完成后会有一个胶囊块被切割成两个等大的图形来作为投票的两个选项,中间由PK两字分隔开点击左边选项,两个图形会随着选择人数…...
服务器端(Debian 12)配置jupyter与R 语言的融合
融合前: 服务器端Debian 12,域名:www.leyuxy.online 1.安装r-base #apt install r-base 2.进入R并安装IRkernel #R >install.packages(“IRkernel”) 3.通过jupyter notebook的Terminal执行: R >IRkernel::installspec() 报错 解决办…...

C语言---指针的两个运算符:点和箭头
目录 点(.)运算符箭头(->)运算符需要注意实际例子 C语言中的指针是一种特殊的变量,它存储了一个内存地址。点(.)和箭头(->)是用于访问结构体和联合体成员的运算符。…...
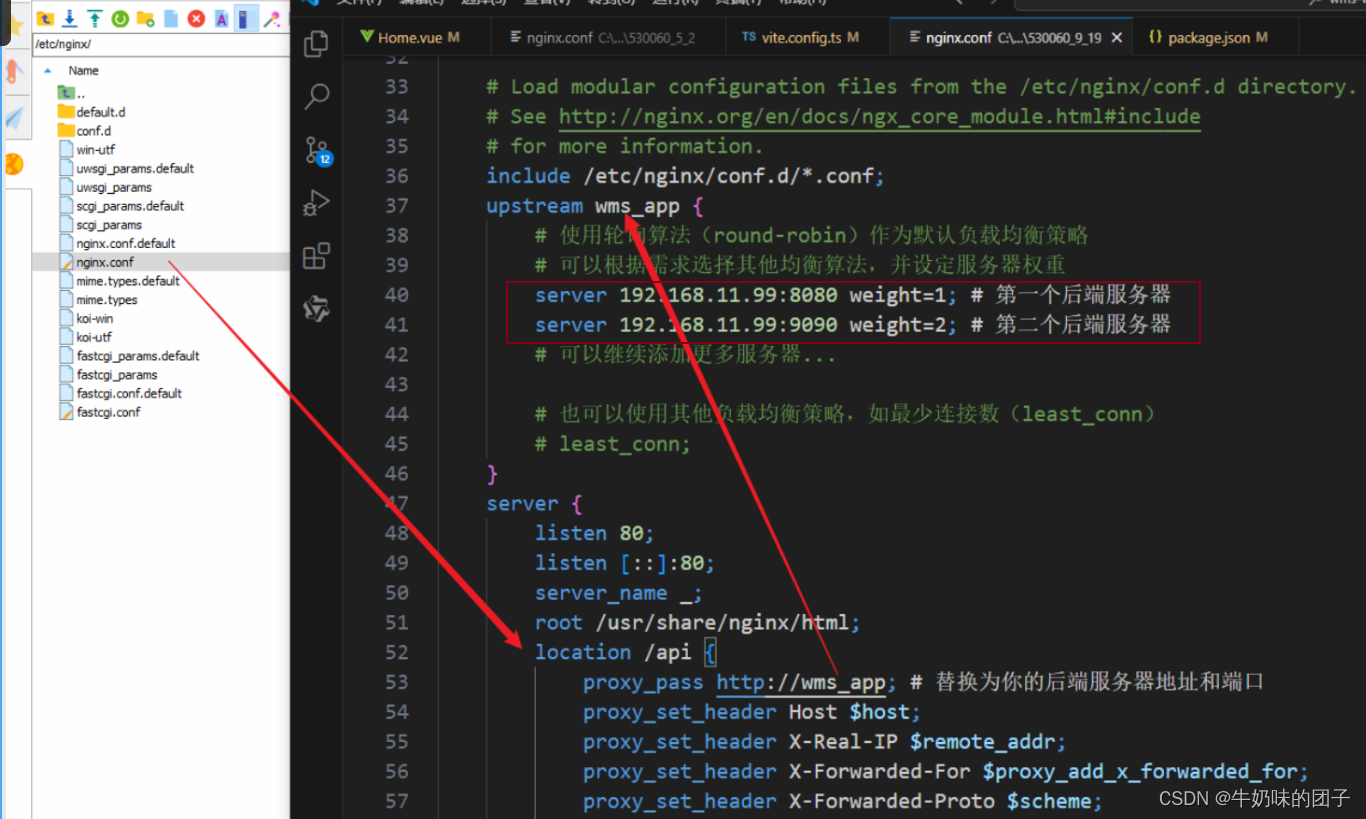
Linux 发布项目到OpenEuler虚拟机
后端:SpringBoot 前端:VUE3 操作系统:Linux 虚拟机:OpenEuler 发布项目是需要先关闭虚拟机上的防火墙 systemctl stop firewalld 一、运行后端项目到虚拟机 1、安装JDK软件包 查询Jdk是否已安装 dnf list installed | grep jd…...
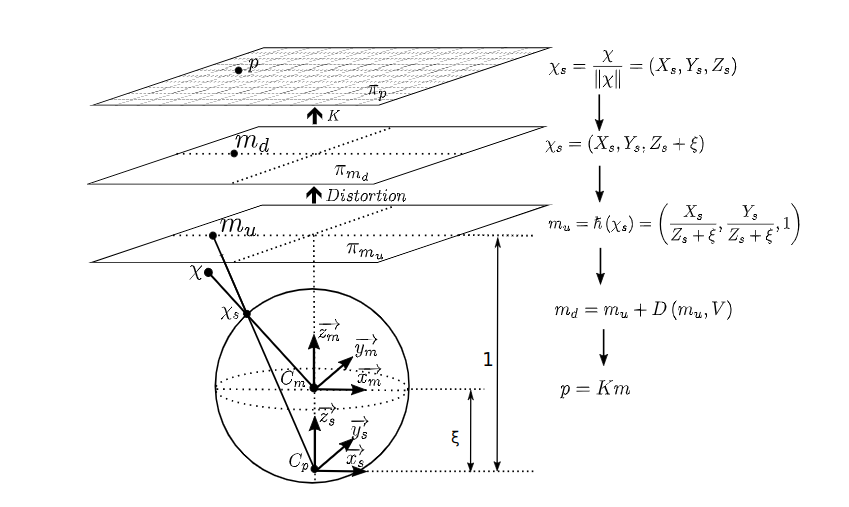
相机与相机模型(针孔/鱼眼/全景相机)
0. 摘要 本文旨在较为直观地介绍相机成像背后的数学模型,主要的章节组织如下: 第1章用最简单的针孔投影模型为例讲解一个三维点是如何映射到图像中的一个像素 第2章介绍除了针孔投影模型外其他一些经典投影模型,旨在让读者建立不同投影模型…...

ARM32day4
1.思维导图 2.实现三个LED灯亮灭 .text .global _start _start: 使能GPIO外设时钟 LDR R0,0x50000A28 LDR R1,[R0]使能GPIOE ORR R1,R1,#(0X1<<4)使能GPIOF ORR R1,R1,#(0X1<<5) STR R1,[R0]设置引脚状态 LDR R0,0X50006000 LDR R1,[R0] 设置PE10为输出 BIC…...

从零开始写 Docker(六)---实现 mydocker run -v 支持数据卷挂载
本文为从零开始写 Docker 系列第六篇,实现类似 docker -v 的功能,通过挂载数据卷将容器中部分数据持久化到宿主机。 完整代码见:https://github.com/lixd/mydocker 欢迎 Star 推荐阅读以下文章对 docker 基本实现有一个大致认识: …...
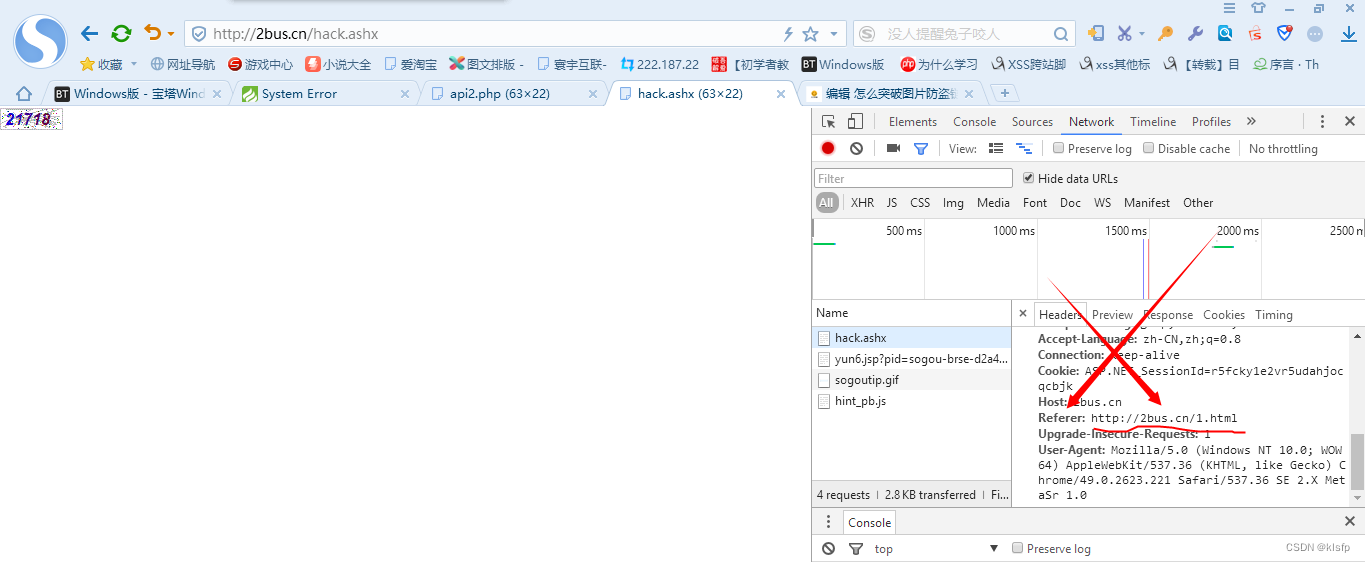
网站引用图片但它域名被墙了或者它有防盗链,我们想引用但又不能显示,本文附详细的解决方案非常简单!
最好的办法就是直接读取图片文件,用到php中一个常用的函数file_get_contents(图片地址),意思是读取远程的一张图片,在输出就完事。非常简单~话不多说,直接上代码 <?php header("Content-type: image/jpeg&quo…...

Java八股文(RabbitMQ)
Java八股文のRabbitMQ RabbitMQ RabbitMQ RabbitMQ 是什么?它解决了哪些问题? RabbitMQ 是一个开源的消息代理中间件,用于在应用程序之间进行可靠的异步消息传递。 它解决了应用程序间解耦、消息传递、负载均衡、故障恢复等问题。 RabbitMQ …...
)
科研学习|论文解读——一种用于短文本消息中的释义检测的深度网络模型(IPM, 2018)
论文原标题 A deep network model for paraphrase detection in short text messages 摘要 本文研究释义检测,即识别语义相同的句子。检测用自然语言编写的相似句子的能力对一些应用程序至关重要,如文本挖掘、文本摘要、剽窃检测、作者身份认证和问题回答。认识到这一…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Web)下篇
onRequestSelected onRequestSelected(callback: () > void) 当Web组件获得焦点时触发该回调。 示例: // xxx.ets import web_webview from ohos.web.webviewEntry Component struct WebComponent {controller: web_webview.WebviewController new web_webv…...
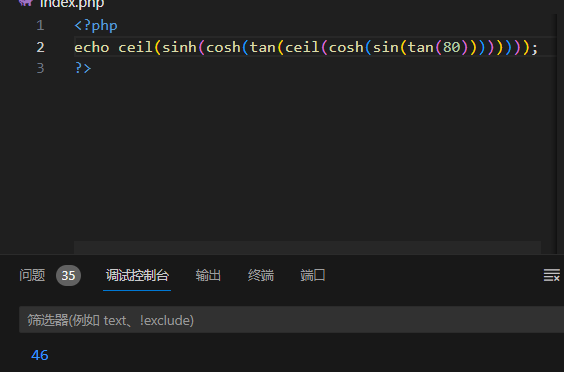
3月19日做题
[NPUCTF2020]验证🐎 if (first && second && first.length second.length && first!second && md5(firstkeys[0]) md5(secondkeys[0]))用数组绕过first1&second[1] 这里正则规律过滤位(Math.) (?:Math(?:\.\w)?) : 匹配 …...
Java8中Stream流API最佳实践Lambda表达式使用示例
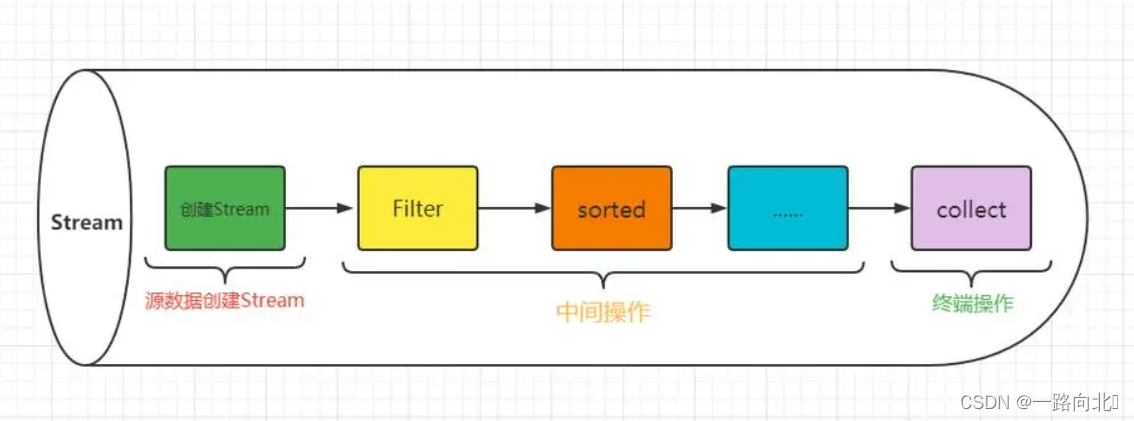
文章目录 一、创建流二、中间操作和收集操作筛选 filter去重distinct截取跳过映射合并多个流是否匹配任一元素:anyMatch是否匹配所有元素:allMatch是否未匹配所有元素:noneMatch获取任一元素findAny获取第一个元素findFirst归约数值流的使用中…...

构建Helm chart和chart使用管道与函数简介
目录 一.创建helm chart(以nginx为例) 1.通过create去创建模板 2.查看模板下的文件 3.用chart模版安装nginx 二.版本更新和回滚问题 1.使用upgrade -f values.yaml或者命令行--set来设置 2.查看历史版本并回滚 三.helm模板内管道和函数 1.defau…...

深入理解OnCalculate函数的运行机制
文章目录 一、学习 OnCalculate 函数的运行原理的意义二、OnCalculate 函数原型三、OnCalculate 函数在MT4与MT5区别四、OnCalculate 函数的运行原理 一、学习 OnCalculate 函数的运行原理的意义 OnCalculate函数是MQL语言中的一个重要函数,它用于计算技术指标的值。…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
