矩阵消元-MIT
文章目录
- 1. 行变换消元法,XA 左乘行变换
1. 行变换消元法,XA 左乘行变换
- 假设我们有一个方程组表示如下:
x + 2 y + z = 2 ; 3 x + 8 y + z = 12 ; 4 y + z = 2 (1) x+2y+z=2;\quad 3x+8y+z=12;\quad4y+z=2\tag{1} x+2y+z=2;3x+8y+z=12;4y+z=2(1) - 矩阵表示如下:
[ 1 2 1 3 8 1 0 4 1 ] → [ 1 2 1 0 2 − 2 0 4 1 ] → [ 1 2 1 0 2 − 2 0 0 5 ] (2) \begin{bmatrix}1&2&1\\\\3&8&1\\\\0&4&1\end{bmatrix}\rightarrow\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&4&1\end{bmatrix}\rightarrow\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&0&5\end{bmatrix}\tag{2} 130284111 → 1002241−21 → 1002201−25 (2) - 矩阵右乘AX列变换,矩阵左乘XA行变换
- 第一行乘以-3 加到第二行,矩阵表示如下:
[ 1 0 0 − 3 1 0 0 0 1 ] [ 1 2 1 3 8 1 0 4 1 ] = [ 1 2 1 0 2 − 2 0 4 1 ] (3) \begin{bmatrix}1&0&0\\\\-3&1&0\\\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&1\\\\3&8&1\\\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&4&1\end{bmatrix}\tag{3} 1−30010001 130284111 = 1002241−21 (3) - 第二行乘以-2 加到第三行,矩阵表示如下:
[ 1 0 0 0 1 0 0 − 2 1 ] [ 1 2 1 0 2 − 2 0 4 1 ] = [ 1 2 1 0 2 − 2 0 0 5 ] (4) \begin{bmatrix}1&0&0\\\\0&1&0\\\\0&-2&1\end{bmatrix}\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&0&5\end{bmatrix}\tag{4} 10001−2001 1002241−21 = 1002201−25 (4) - 小结:可以用矩阵形式表示消元如下:
[ 1 0 0 0 1 0 0 − 2 1 ] [ 1 0 0 − 3 1 0 0 0 1 ] [ 1 2 1 3 8 1 0 4 1 ] = [ 1 2 1 0 2 − 2 0 0 5 ] (5) \begin{bmatrix}1&0&0\\\\0&1&0\\\\0&-2&1\end{bmatrix}\begin{bmatrix}1&0&0\\\\-3&1&0\\\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&1\\\\3&8&1\\\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\\\0&2&-2\\\\0&0&5\end{bmatrix}\tag{5} 10001−2001 1−30010001 130284111 = 1002201−25 (5) - 上述矩阵转换成方程组可得:
x + 2 y + z = 2 2 y − 2 z = 6 5 z = − 10 (6) \begin{aligned}x+2y+z=2\\\\2y-2z=6\\\\5z=-10\end{aligned}\tag{6} x+2y+z=22y−2z=65z=−10(6) - 得出结果如下:
x = 2 ; y = 1 ; z = − 2 (7) x=2;\quad y=1\quad ;z=-2\tag{7} x=2;y=1;z=−2(7) - 小结
A X = b → 表示的是矩阵 A 的列向量通过 X 进行右乘列变换求和得到 b (8) AX=b\rightarrow 表示的是矩阵A的列向量通过 X 进行右乘列变换求和得到b\tag{8} AX=b→表示的是矩阵A的列向量通过X进行右乘列变换求和得到b(8)
Y A = c → 表示的是矩阵 A 的行向量通过 Y 进行左乘行变换求和得到 c (9) YA=c\rightarrow 表示的是矩阵A的行向量通过 Y 进行左乘行变换求和得到c\tag{9} YA=c→表示的是矩阵A的行向量通过Y进行左乘行变换求和得到c(9)
相关文章:

矩阵消元-MIT
文章目录 1. 行变换消元法,XA 左乘行变换 1. 行变换消元法,XA 左乘行变换 假设我们有一个方程组表示如下: x 2 y z 2 ; 3 x 8 y z 12 ; 4 y z 2 (1) x2yz2;\quad 3x8yz12;\quad4yz2\tag{1} x2yz2;3x8yz12;4yz2(1)矩阵表示如下: [ 1 2 1 3 8 1…...
基于nodejs+vue班级管理系统的设计与实现-flask-django-python-php
随着电子技术的普及和快速发展,线上管理系统被广泛的使用,有很多事业单位和商业机构都在实现电子信息化管理,班级管理系统也不例外,由比较传统的人工管理转向了电子化、信息化、系统化的管理。随着互联网技术的高速发展࿰…...

2024年起,游戏开发团队62%的从业人员使用AI智能技术
易采游戏网3月19日消息:游戏引擎制造商最新发布的《Unity》报告证实,近六成的全球游戏开发团队已在各个环节全面采用人工智能技术,以大幅提升生产效率并节约宝贵时间。 伴随着科技的快速发展,游戏开发领域逐渐转向借助人工智能技术…...

mysql 主从复制、读写分离、高可用
MySQL 的主从复制、读写分离和高可用性是数据库架构中常见的概念,它们旨在提高数据库的可靠性、性能和可扩展性。下面我将分别解释这三个概念: 1. MySQL 主从复制 主从复制 是 MySQL 中的一个功能,允许数据从一个 MySQL 数据库服务器&#…...

力扣爆刷第100天之hot100五连刷86-90
力扣爆刷第100天之hot100五连刷86-90 文章目录 力扣爆刷第100天之hot100五连刷86-90一、139. 单词拆分二、300. 最长递增子序列三、152. 乘积最大子数组四、416. 分割等和子集五、32. 最长有效括号 一、139. 单词拆分 题目链接:https://leetcode.cn/problems/word-…...
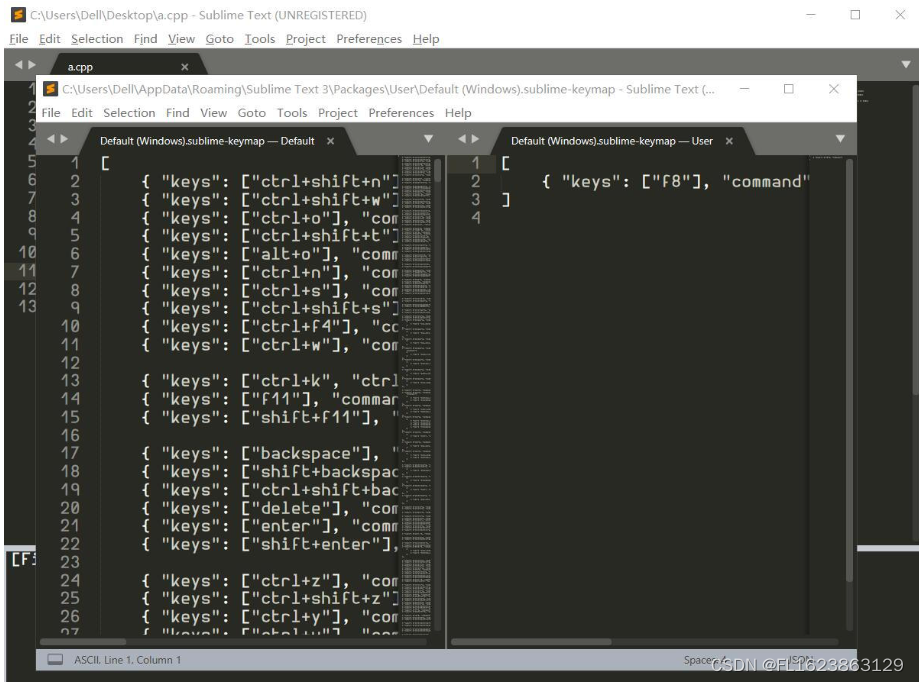
Sublime Text3 C/C++一键调试运行代码
minGW的系统环境配置: 使用的C/C编译器是minGW,点此进入官网链接,下载后需要在线安装,安装后需要将安装目录下的bin目录所在路径加入path环境变量。本菜鸡的电脑里安装了CodeBlocks,在CodeBlocks的安装目录下有MinGW&…...

robots协议详解:爬虫也要有边界感
随着互联网的迅猛发展,信息的获取变得越来越便捷,而网络爬虫(Spider)技术就是其中之一。网络爬虫是一种自动化程序,它能够遍历互联网上的网页,提取信息,用于各种用途,例如搜索引擎索引、数据挖掘、价格比较等。但是,爬虫技术虽然强大,但是也是一把双刃剑,在正当使用…...

C#面:简述 var 和 dynamic
var 关键字: var 关键字是在编译时进行类型推断的。也就是说,编译器会根据变量的初始化表达式来确定变量的类型,并在编译时将其替换为实际的类型。var 关键字只能用于局部变量,不能用于字段、方法参数或返回类型。var 关键字声明…...

S32 Design Studio PE工具配置DMA
工具配置 DMA位置跟设备不一样,在Referenced_components里面。 Configurations里面就默认配置就行 channels是比较重要的,一条信号传输用到一个通道。可以选择UART、ADC、CAN之类的,这里用在了SPI通讯里面。 生成代码 在 Generated_Code\dm…...

【Effective C++】36绝不重新定义继承而来的non-virtual 函数
例子如下: class B { public:void mf(); };class D : public B {};D x; // x是一个类型为D的对象 // 方式一 B* pB &x // 获得一个pB 指向 x pB->mf(); // 经由指针调用mf// 方式二 D* pD &x // 获得一个指针指向x pD->mf(); // 经由指针调用mf我…...
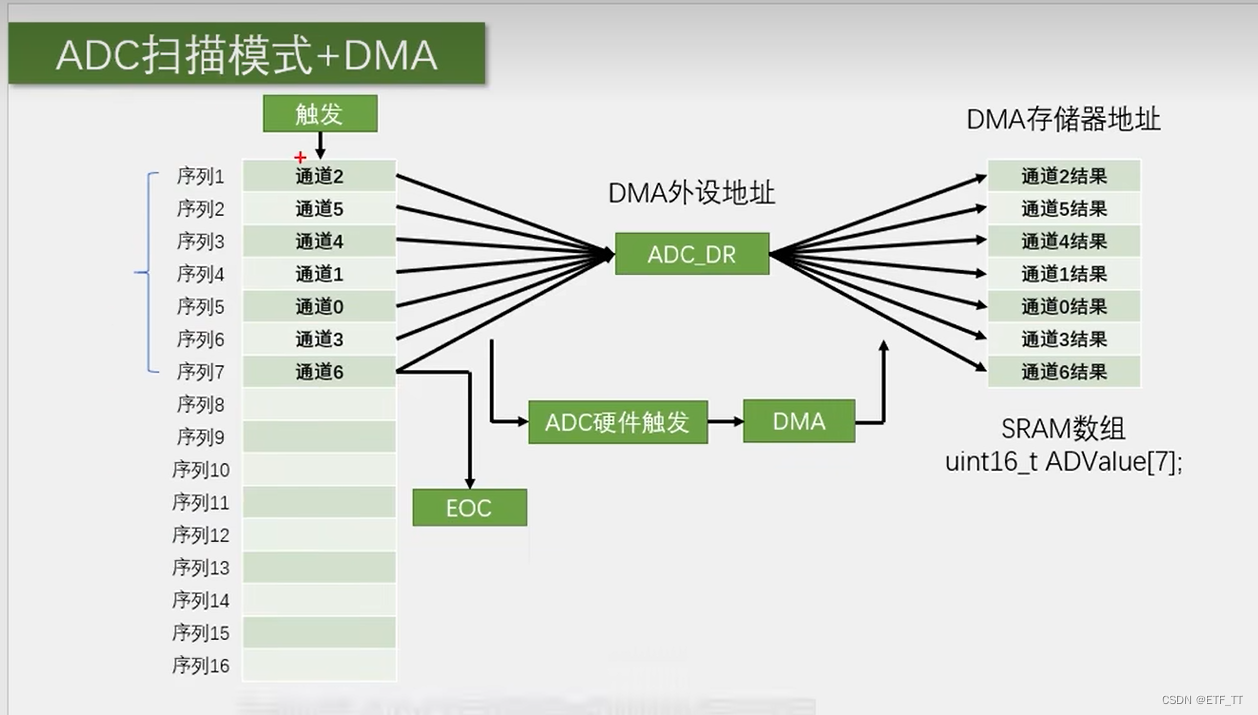
STM32-DMA数据转运
DMA进行转运的条件 1:开关控制,DMA_CMD必须使能2:传输计数器必须大于03:触发源必须有触发的信号...

Vue 3 + TypeScript 项目中全局挂载并使用工具函数
一、proxy方式 1.封装日期选择工具函数: 在untils文件夹下新建index.ts,并导出工具函数 /*** 获取不同类型日期* param:类型 dateVal: 是否指定*/ export function getSystemDate(param: any, dateVal: any) {let systemDate dateVal ? new Date(da…...

第二门课:改善深层神经网络<超参数调试、正则化及优化>-超参数调试、Batch正则化和程序框架
文章目录 1 调试处理2 为超参数选择合适的范围3 超参数调试的实践4 归一化网络的激活函数5 将Batch Norm拟合进神经网络6 Batch Norm为什么会奏效?7 测试时的Batch Norm8 SoftMax回归9 训练一个SoftMax分类器10 深度学习框架11 TensorFlow 1 调试处理 需要调试的参…...
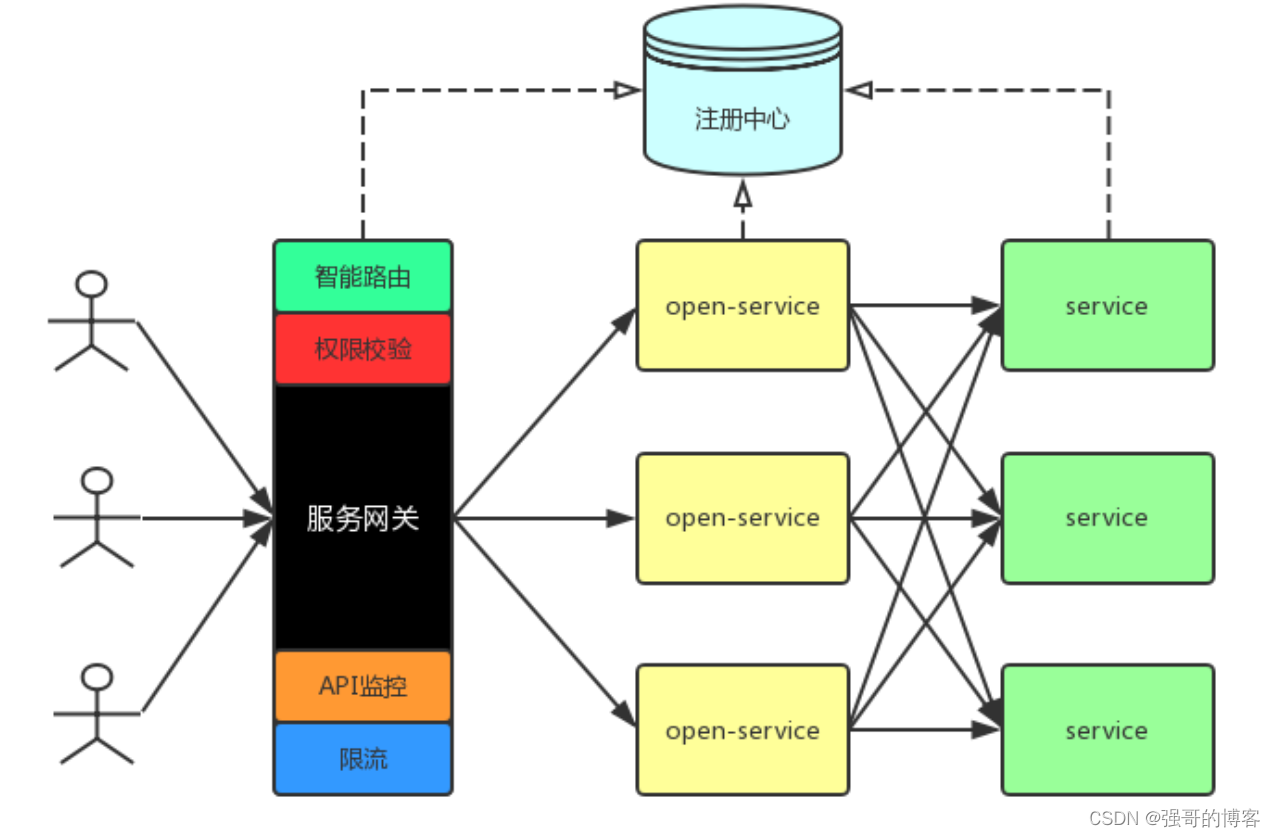
漫谈微服务网关
一、什么是服务网关 服务网关 路由转发 过滤器 1、路由转发:接收一切外界请求,转发到后端的微服务上去; 2、过滤器:在服务网关中可以完成一系列的横切功能,例如权限校验、限流以及监控等,这些都可以通过…...

进击的PostgreSQL
目录 前言 一、什么是PostgreSQL 1.PostgreSQL的定义 2.PostgreSQL功能和特性 2.1数据类型 2.2数据完整性 2.3并发性、性能 2.4可靠性、灾难恢复 2.5安全 2.6扩展 2.7国际化、文本搜索 二、部署PostgreSQL 1.下载与安装 2.配置数据库 3.配置远程访问 4.修改配置…...
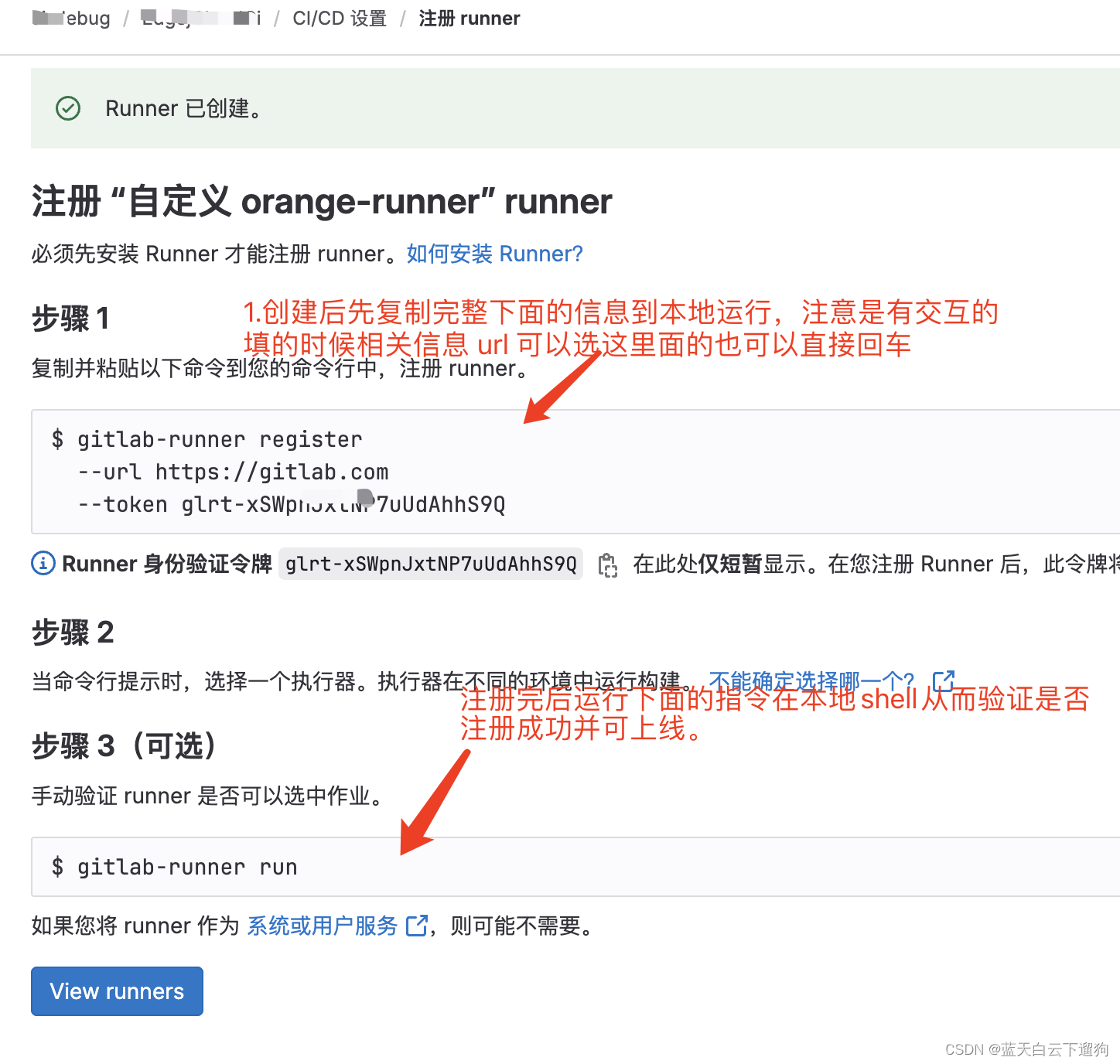
本地gitlab-runner的创建与注册
引言 之前通过一些方式在本地创建runner,时而会出现一些未知的坑,所以写下本文记录runner可以无坑创建的方式。 以下注册runner到相应仓库的前提是已经在本地安装了gitlab-runner 具体安装方式见官网 本地gitlab-runner安装常用的指令 查看gitlab r…...

《UE5_C++多人TPS完整教程》学习笔记28 ——《P29 Mixamo 动画(Mixamo Animations)》
本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P29 Mixamo动画(Mixamo Animations)》 的学习笔记,该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版,UP主(也是译者…...

剑指offer力扣题集
剑指offer Krahets前辈整理的题解,这个博客为了方便自己刷题和复习,加油! 01. 数组中重复的数字 力扣链接 02. 二维数组中的查找 力扣链接 03. 替换空格 力扣链接 04. 从尾到头打印链表 力扣链接 05. 重建二叉树 力扣链接好难 -_-…...

【商业|数据科学主题会议推荐】2024年商业分析与数据科学国际学术会议(ICBADS 2024)
【商业|数据科学主题会议推荐】2024年商业分析与数据科学国际学术会议(ICBADS 2024) 征稿主题 (以下主题包括但不限于) 多媒体决策 决策理论与决策科学 数字市场设计与运营 降维 电子商务 道德决策 财务分析 群体决策与软件 医疗保…...

爬虫技术实战案例解析
目录 前言 案例背景 案例实现 案例总结 结语 前言 作者简介: 懒大王敲代码,计算机专业应届生 今天给大家聊聊爬虫技术实战案例解析,希望大家能觉得实用! 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
