数位DP
数位dp的题目一般会问,某个区间内,满足某种性质的数的个数。
- 利用前缀和,比如求区间[l,r]中的个数,转化成求[0,r]的个数 [0,l-1]的个数。
- 利用树的结构来考虑(按位分类讨论)
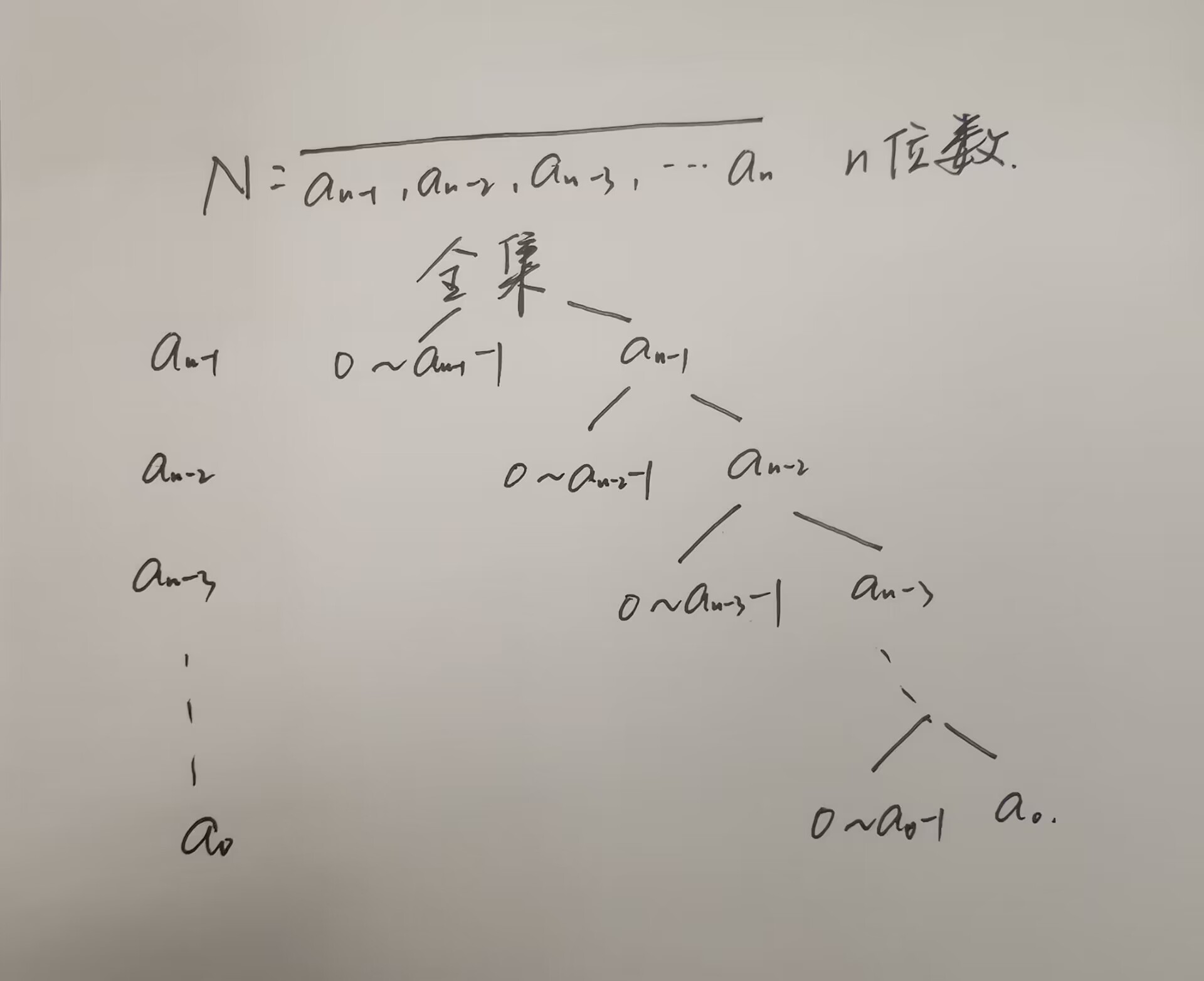
1081. 度的数量
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int f[N][N],l,r,K,B;
//预处理组合数
int init()
{for(int i=0;i<N;i++)for(int j=0;j<=i;j++)if(!j) f[i][j]=1;else f[i][j]=f[i-1][j]+f[i-1][j-1];
}int dp(int n)
{if(!n) return 0;vector<int>vec;while(n) vec.push_back(n%B),n/=B;//十进制转成B进制int res=0,last=0;//res记录答案数,last表示用了多少个1for(int i=vec.size()-1;i>=0;i--){int x=vec[i];//取出第i位数if(x)//(如果当前位x==0直接进入右分支,讨论下一位){res+=f[i][K-last];//当前位填0,从剩下的所有位(共有i位)中选K-last个数。//对应于:左分支中0的情况,合法if(x>1){res+=f[i][K-last-1];break;}else//x==1,直接讨论下一位,可用的1的个数减1{last++;if(last>K) break;}}if(i==0&&last==K) res++;//遍历到最后一位且最后一位取1}return res;
}
int main()
{init();cin>>l>>r>>K>>B;cout<<dp(r)-dp(l-1)<<endl;return 0;
}
1082. 数字游戏
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数int init()
{for(int j=0;j<=9;j++) f[1][j]=1;for(int i=2;i<N;i++)for(int j=0;j<=9;j++)for(int k=j;k<=9;k++)f[i][j]+=f[i-1][k];
}int dp(int n)
{if(!n) return 1;vector<int>vec;while(n) vec.push_back(n%10),n/=10;int res=0,last=0;//res记录答案数,last表示上一位的数字for(int i=vec.size()-1;i>=0;i--){int x=vec[i];//取出第i位数if(last>x) break;//这一位数无论怎么取都比上一位小for(int j=last;j<vec[i];j++)//进入左分支讨论res+=f[i+1][j];last=x;//更新latif(!i) res++;//到了最后一位,剩下一种合法的情况}return res;
}
int main()
{init();while(cin>>l>>r)cout<<dp(r)-dp(l-1)<<endl;return 0;
}
1083. Windy数
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数
//存的是(包含前导零)的情况
int init()
{for(int j=0;j<=9;j++) f[1][j]=1;for(int i=2;i<N;i++)for(int j=0;j<=9;j++)for(int k=0;k<=9;k++)if(abs(j-k)>=2) f[i][j]+=f[i-1][k];
}
int dp(int n)
{if(!n) return 0;vector<int>vec;while(n) vec.push_back(n%10),n/=10;int res=0,last=-2;//res记录答案数,last表示上一位的数字for(int i=vec.size()-1;i>=0;i--){int x=vec[i];//取出第i位数for(int j=(i==vec.size()-1);j<x;j++)//首位不能取到零,其他位可以if(abs(j-last)>=2) res+=f[i+1][j];if(abs(x-last)>=2) last=x;else break;if(!i) res++;}for(int i=1;i<vec.size();i++)for(int j=1;j<=9;j++)res+=f[i][j];//特判首位为零的情况return res;
}int main()
{init();cin>>l>>r;cout<<dp(r)-dp(l-1)<<endl;return 0;
}
1084. 数字游戏 II
f[i][j][k] 表示一共有i位,且最高位数字是j,且所有位数字和%P结果为k的数的个数,若要转移到f[i][j][k]的状态,在i-1位对于每个x(x取值0~9)都应使第三维为(k-j)%P
状态转移方程:
f[i][j][k]=∑k=0P−1∑x=09f[i−1][x][(k−j)%P]f[i][j][k]=\sum_{k=0}^{P-1}\sum_{x=0}^{9}f[i-1][x][(k-j)\%P]f[i][j][k]=∑k=0P−1∑x=09f[i−1][x][(k−j)%P]
用last表示到当前为止,前面数位上的数字之和,对此,当前第i位数字为j,前面数字之和为last,那么
后i位(包括j这一位)数字之和sum与last的关系就是
(last+sum)%N==0,那么sum%N==(-last)%N,
所以res+=f[i+1][j][(-last%N)];
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N][110],l,r,P;
//f[i][j][k]表示一共有i位,且最高位数字是j,且所有位数字和%P结果为k的数的个数
int mod(int u,int v)
{return (u%v+v)%v;
}
int init()
{memset(f,0,sizeof f);for(int i=0;i<=9;i++) f[1][i][i%P]++;for(int i=2;i<N;i++)for(int j=0;j<=9;j++)for(int k=0;k<P;k++)for(int x=0;x<=9;x++)f[i][j][k]+=f[i-1][x][mod(k-j,P)];
}int dp(int n)
{if(!n) return 1;vector<int>vec;while(n) vec.push_back(n%10),n/=10;int res=0,last=0;//res记录答案数,last表示前面所有位数上数字的和for(int i=vec.size()-1;i>=0;i--){int x=vec[i]; for(int j=0;j<x;j++) //第i位放0~x-1res+=f[i+1][j][mod(-last,P)]; //0~i位,所以一共有i+1位last+=x;if(!i&&last%P==0) res++;}return res;
}int main()
{while(cin>>l>>r>>P){init();cout<<dp(r)-dp(l-1)<<endl;}return 0;
}
1085. 不要62
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int f[N][N],l,r;
//f[i][j]表示一共有i位,且最高位为j的数的个数int init()
{for(int j=0;j<=9;j++) if(j!=4) f[1][j]=1;//一位不含5for(int i=2;i<N;i++)for(int j=0;j<=9;j++){if(j==4) continue;for(int k=0;k<=9;k++){if(k==4||(j==6&&k==2)) continue;f[i][j]+=f[i-1][k];}}
}
int dp(int n)
{if(!n) return 1;vector<int>vec;while(n) vec.push_back(n%10),n/=10;int res=0,last=0;//res记录答案数,last表示上一位的数字for(int i=vec.size()-1;i>=0;i--){int x=vec[i];//取出第i位数for(int j=0;j<x;j++) {if(j==4||(j==2&&last==6)) continue;res+=f[i+1][j];}if(x==4||(x==2&&last==6)) break;last=x;if(!i) res++;}return res;
}int main()
{init();while(cin>>l>>r,l||r)cout<<dp(r)-dp(l-1)<<endl;return 0;
}
相关文章:

数位DP
数位dp的题目一般会问,某个区间内,满足某种性质的数的个数。 利用前缀和,比如求区间[l,r]中的个数,转化成求[0,r]的个数 [0,l-1]的个数。利用树的结构来考虑(按位分类讨论) 1081. 度的数量 #include<…...
-链表)
剑指offer(一)-链表
(一)找出链表的环的入口结点 JZ23 链表中环的入口结点 中等 通过率:36.78% 时间限制:1秒 空间限制:64M 知识点链表哈希双指针 描述 给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点…...
CDH大数据平台入门篇之搭建与部署
一、CDH介绍 1.CDH 是一个强大的商业版数据中心管理工具 提供了各种能够快速稳定运行的数据计算框架,如Spark; 使用Apache Impala做为对HDFS、HBase的高性能SQL查询引擎; 使用Hive数据仓库工具帮助用户分析数据; 提供CM安装HBas…...

Spark Join
Spark Join关联形式内关联外关联左外关联右外关联全外关联左半/逆关联关联机制NLJSMJHJ分发模式Join 选择等值 Join不等值 JoinJoin 按照关联形式(Join Types)划分 : 内关联、外关联、左关联、右关联 Join 按实现机制划分 : NLJ (Nested Loop Join) 、S…...

数字的转化规则?
数字的转化规则?js将字符串转换为数字的方式有哪些?1. 使用 parseInt()2. 使用 Number()3. 使用一元运算符 ()4.使用parseFloat()5. 使用 Math.floor()和Math.ceil()6.乘以数字7. 双波浪号 (~~) 运算符其它值到数字的转化规则1.Undefined 类型2.Null 类型…...

MySQL面试题-锁相关
目录 1.MySQL 锁的类型有哪些呢? 2.如何使用全局锁 3.如果要全库只读,为什么不使用set global readonlytrue的方式? 4.表级锁和行级锁有什么区别? 5.行级锁的使用有什么注意事项? 6.InnoDB 有哪几类行锁ÿ…...

Windows 终端编译 C代码
E:\My_SoftWare\Window gcc\windowbianji\mingw64\bin 此电脑--》属性--》系统--》高级系统设置--》环境变量--》Path--》新建--》粘贴路径 E:\My_SoftWare\Window gcc\windowbianji\mingw64\bin 打开命令终端 E: 回车 dir 显示所有文件 cd E:\My_SoftWare\Window gcc\C_co…...
SpringCloud:Feign的使用及配置
目录 Feign的使用及配置 1、Feign替代RestTemplate 2、使用Fegin步骤 3、自定义配置 4、Feign使用优化 5、Feign的最佳实践方式 Feign的使用及配置 1、Feign替代RestTemplate RestTemplate方式远程调用的问题 问题: 1、代码可读性差,编程体验不同…...

Parquet学习与使用之BloomFilter的应用
写在前面 最近在自己做自定义的OLAP系统,文件格式上用的是Parquet,但是发现Parquet各个API的示例代码很少。所以就打算把这个系列的文章写一下。 1. Parquet的Filter Parquet的过滤支持两大类,一类是基于Footer中的元数据进行RowGroup级别…...

95%置信区间计算-理解
机器学习中做多次试验后,需要计算指标的95%置信区间。 假设做了10次试验,计算得出的某指标分别为{x1,…,x10} 其均值为μ(x1...x10)/10\mu(x1 ... x10)/10μ(x1...x10)/10 方差σ∑(xi−μ)2/10\sigma\sum(x_i -\mu)^2/10σ∑(xi−μ)2/10 95%置信…...
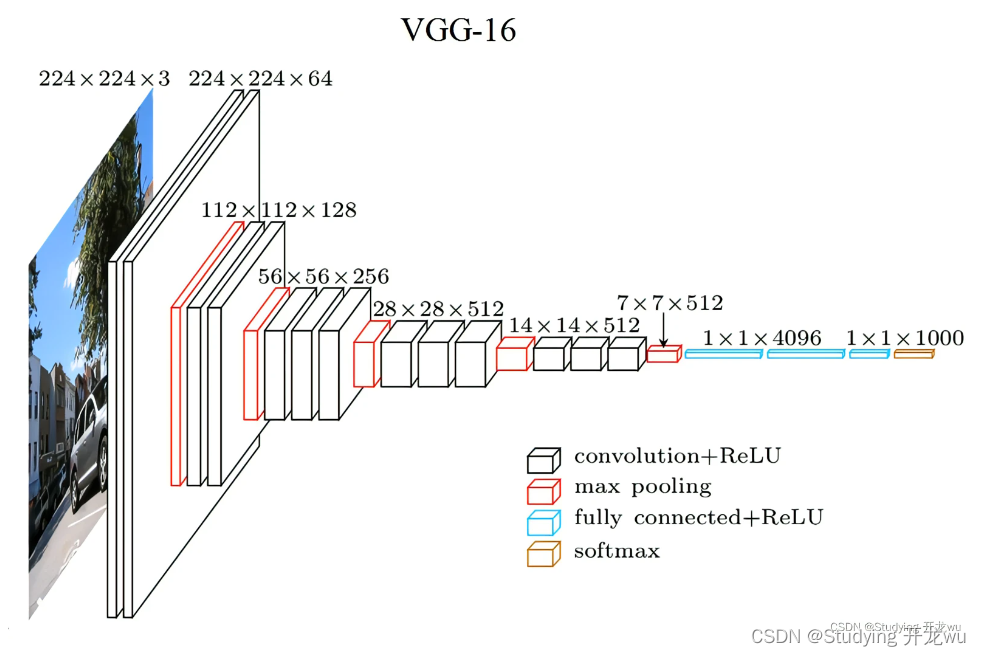
深度学习pytorch实战三:VGG16图像分类篇自建数据集图像分类三类
1.自建数据集与划分训练集与测试集 2.模型相关知识 3.model.py——定义AlexNet网络模型 4.train.py——加载数据集并训练,训练集计算损失值loss,测试集计算accuracy,保存训练好的网络参数 5.predict.py——利用训练好的网络参数后,…...

2023年3月软考高项(信息系统项目管理师)报名走起!!!
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...
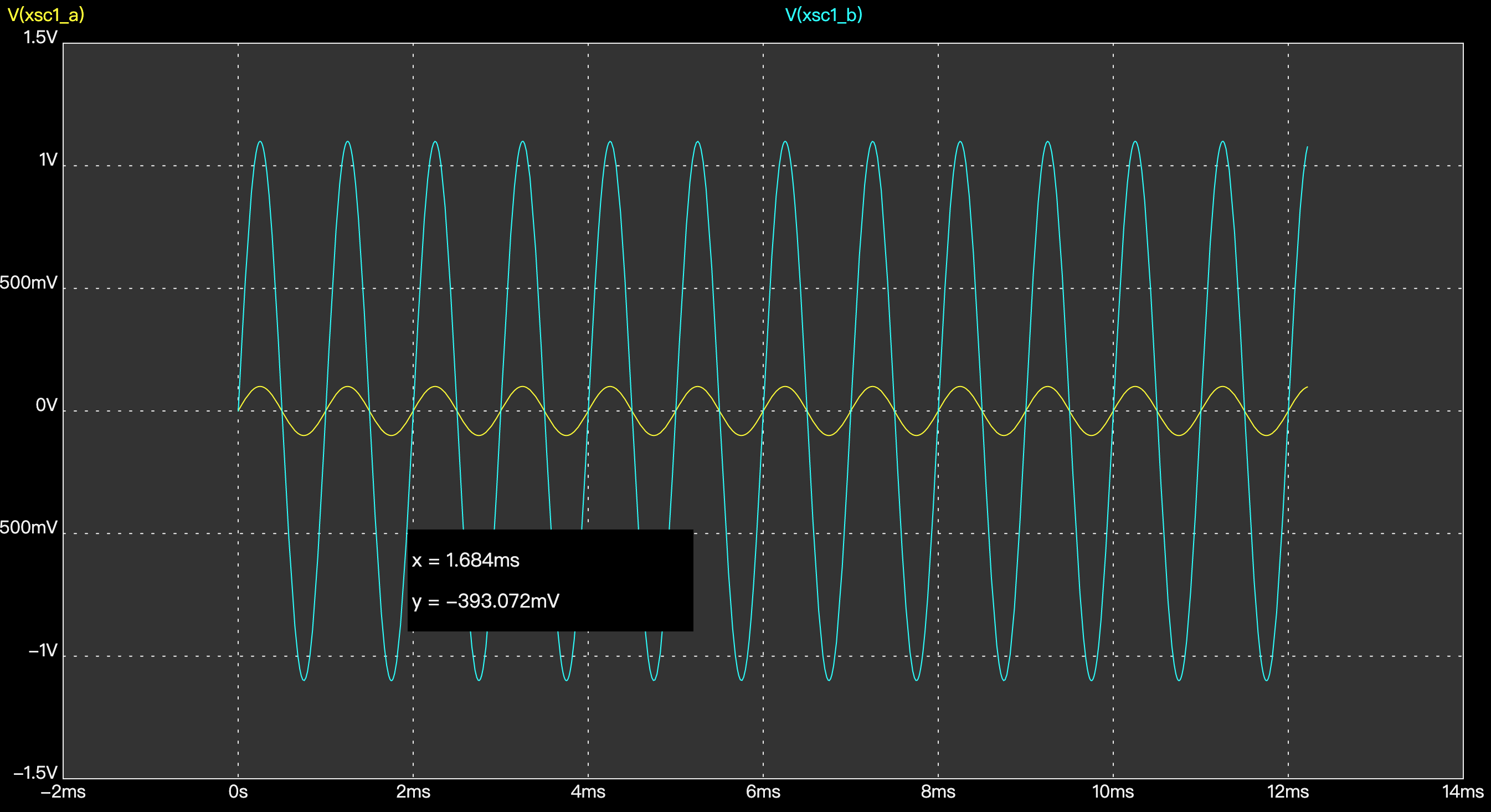
模电学习11 运算放大器学习入门
一、基本概念 运算放大器简称运放,是一种模拟电路实现的集成电路,可以对信号进行很高倍数的放大。一般有正相输入端、反相输入端、输出端口、正电源、负电源等接口。 运放可工作在饱和区、放大区,其中放大区极其陡峭,因为运放的放…...

spring学习3.5
Bean是什么 Spring里面的Bean就类似是定义的一个组件,而这个组件的作用就是实现某个功能的,这里所定义的Bean就相当于给了你一个更为简便的方法来调用这个组件去实现你要完成的功能。 IoC是什么 谁控制谁,控制什么? 传统Java SE程…...

名创优品:国内“触礁”,海外“提速”
在互联网经济十分发达、实体经济不太景气的时代背景下,自有品牌零售商代表名创优品却逆势而上,开始向着全球品牌类生活用品零售市场发起冲击,并凭借着“极致性价比大规模跑量”的独特优势在该领域取得了十分可观的成绩。 随着“Z时代”人群逐…...
Java学习笔记 --- Tomcat
一、JavaWeb 的概念 JavaWeb 是指,所有通过 Java 语言编写可以通过浏览器访问的程序的总称,叫 JavaWeb。 JavaWeb是基于请求和响应来开发的。请求是指客户端给服务器发送数据,叫请求 Request。 响应是指服务器给客户端回传数据,叫…...

面向对象设计模式:行为型模式之状态模式
文章目录一、引入二、状态模式2.1 Intent 意图2.2 Applicability 适用性2.3 类图2.4 Collaborations 合作2.5 Implementation 实现2.5 状态模式与策略模式的对比2.5 状态模式实例:糖果机2.6 状态模式实例:自行车升降档一、引入 State Diagram 状态图&am…...

【Python入门第二十五天】Python 作用域
变量仅在创建区域内可用。这称为作用域。 局部作用域 在函数内部创建的变量属于该函数的局部作用域,并且只能在该函数内部使用。 实例 在函数内部创建的变量在该函数内部可用: def myfunc():x 100print(x)myfunc()运行实例 100函数内部的函数 如…...
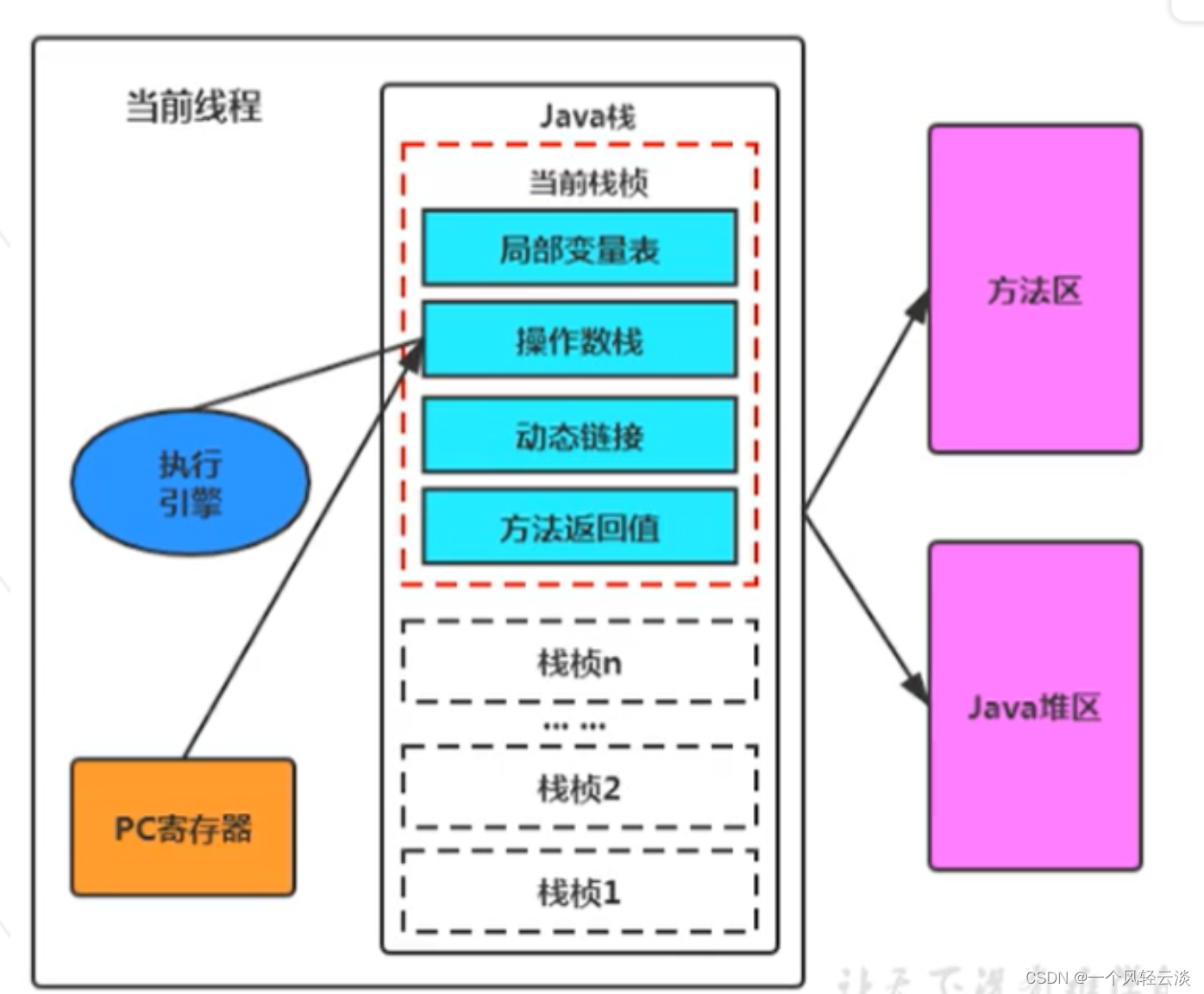
运行时数据区及程序计数器
运行时数据区 概述 运行时数据区,也就是下图这部分,它是在类加载完成后的阶段 当我们通过前面的:类的加载-> 验证 -> 准备 -> 解析 -> 初始化 这几个阶段完成后,就会用到执行引擎对我们的类进行使用,同时…...
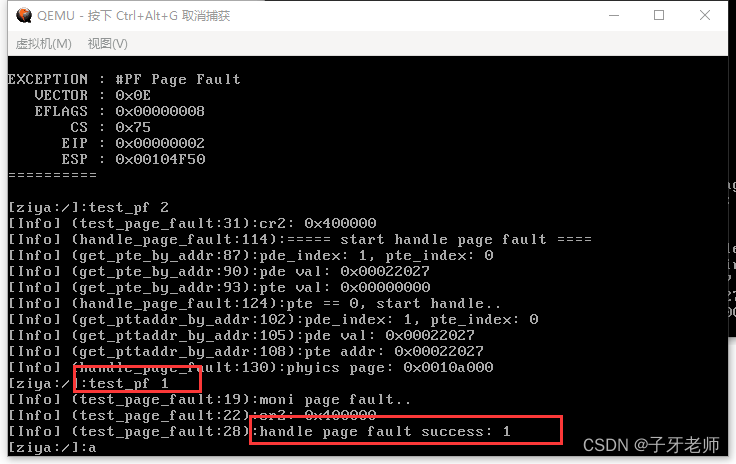
手写操作系统+文件系统开源啦
哈喽,我是子牙,一个很卷的硬核男人。喜欢研究底层,聚焦做那些大家想学没地方学的课程:手写操作系统、手写虚拟机、手写模拟器、手写编程语言… 今年是我创业的第二年,已经做了两个课程:手写JVM、手写操作系…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
