AcWing 727. 菱形——像拼图一样做题
题目描述]
分析:
利用程序根据输入的整数,画出由字符*构成的该整数阶的实心菱形。给出一个示例: n = 7 n=7 n=7。
* * * * * * * * *
* * * * * * * * * * * * * * * *
我们将采取拆解问题,通过四个部分的组合最终拼出这个菱形。通过观察,可以看出不管给出的整数是多少,最终形成的图形一定是一由空格 和星星*构成个正方形(记为s)。如图1所示。


基于此我们可以先将这两条对角线画出来,是不是就成功了一半了呢?这两条对角线也很容易画,一条线是 x = 3 ( n / 2 ) x=3(n/2) x=3(n/2),另一条是 y = n / 2 y=n/2 y=n/2。给出画对角线的代码:
for (int i = 0; i < n; i ++) { // 画出十字架对角线for (int j = 0; j < n; j ++) {if (i == n / 2 || j == n / 2) res[i][j] = '*';}}
通过这一步画出的图形为:
* * *
* * * * * * * * * *
拼出第二部分-左上角
有了这两条相交的对角线,我们只需要处理左上角需要描的点即可,然后利用相交的对角线通过关于 x x x轴对称与 y y y轴对称的方法映射到其他的三个区域!如图3所示。

那么该怎么计算左上角的该描的点呢?我们可以观察这三个点的坐标 ( 1 , 2 ) , ( 2 , 1 ) , ( 2 , 2 ) {(1,2), (2,1), (2, 2)} (1,2),(2,1),(2,2),也可以表示为 ( 1 , n / 2 − 1 ) , ( 2 , 1 ) , ( 2 , n / 2 − 1 ) {(1,n/2-1), (2,1), (2, n/2-1)} (1,n/2−1),(2,1),(2,n/2−1)。因此可以用双层循环进行遍历,伪代码如下:
// 左上角描点for (int i = 1; i <= n / 2 - 1; i ++) { // 1到n/2-1行for (int j = n / 2 - 1; j>= n / 2 - i; j --) { // 倒着来,从n/2-1到n/2-i列res[i][j] = '*';}}
经过这一步,我们所画出来的图形为:
* * * * * *
* * * * * * * * * *
拼出第二部分-右上角
当我们画出左上角后,可以将 n / 2 n/2 n/2视作 y y y轴,进行关于y轴的对称实现映射效果。具体流程为:先遍历一遍左上角,遇到为*的就进行映射,只需要更改列的坐标即可,给出代码:
for (int i = 1; i <= n / 2 - 1; i ++) { // 对称到右上角for (int j = 1; j <= n / 2 - 1; j ++) {if (res[i][j] == '*') {res[i][n / 2 + (n / 2 - j)] = res[i][j];}}}
此时生成的图形为:
* * * * * * * * *
* * * * * * * * * *
接下来该怎么拼?
后面有多种拼法,可以先做左上角/右上角关于 x x x轴的对称,映射到左下角/右下角。这里我将上半部分当作一个整体,进行 x x x轴对称,一步到位!代码为:
for (int i = 1; i <= n - 1; i ++) { // 对称到整个下方for (int j = 1; j <= n - 1; j ++) {if (res[i][j] == '*') {res[n / 2 + (n / 2 - i)][j] = res[i][j];}}}
图像为:
* * * * * * * * *
* * * * * * * * * * * * * * * *
至此,菱形就被我们画出来。这道题有需要不同的画法,上面只是笔者自己的理解,关于其他更优雅更简洁的方法请大家开动脑筋去尽情尝试吧!!
代码(Java)
import java.util.*;public class Main {public static void main(String args[]) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int x = n / 2;char[][] res = new char[n][n];for (int i = 0; i < n; i ++) { // 画出十字架for (int j = 0; j < n; j ++) {if (i == n / 2 || j == n / 2) res[i][j] = '*';}}for (int i = 1; i <= n / 2 - 1; i ++) { // 左上角for (int j = n / 2 - 1; j>= n / 2 - i; j --) {res[i][j] = '*';}}for (int i = 1; i <= n / 2 - 1; i ++) { // 对称到右上角for (int j = 1; j <= n / 2 - 1; j ++) {if (res[i][j] == '*') {res[i][n / 2 + (n / 2 - j)] = res[i][j];}}}for (int i = 1; i <= n - 1; i ++) { // 对称到整个下方for (int j = 1; j <= n - 1; j ++) {if (res[i][j] == '*') {res[n / 2 + (n / 2 - i)][j] = res[i][j];}}}for (int i = 0; i < n; i ++) {for (int j = 0; j < n; j ++) {if (res[i][j] == '*') System.out.print('*');else System.out.print(' ');}System.out.println();}}
}
相关文章:

AcWing 727. 菱形——像拼图一样做题
题目描述] 分析: 利用程序根据输入的整数,画出由字符*构成的该整数阶的实心菱形。给出一个示例: n 7 n7 n7。 * * * * * * * * * * * * * * * * * * * * * * * * * 我们将采取拆解问题,通过四个部分的…...

深入理解生成型大型语言模型:自监督预训练、细调与对齐过程及其应用
分析概述 本文主要介绍了生成型大型语言模型(LLM)的预训练过程,特别是通过下一个令牌(token)预测的自监督学习方法,以及后续的细调(finetuning)和对齐(alignment&#x…...
个人简历主页搭建系列-03:Hexo+Github Pages 介绍,框架配置
今天的更新内容主要是了解为什么选择这个网站搭建方案,以及一些前置软件的安装。 Why Hexo? 首先我们了解一下几种简单的网站框架搭建方案,看看对于搭建简历网站的需求哪个更合适。 在 BuiltWith(网站技术分析工具)上我们可以…...

【堆、位运算、数学】算法例题
目录 十九、堆 121. 数组中的第K个最大元素 ② 122. IPO ③ 123. 查找和最小的K对数字 ② 124. 数据流的中位数 ③ 二十、位运算 125. 二进制求和 ① 126. 颠倒二进制位 ① 127. 位1的个数 ① 128. 只出现一次的数字 ① 129. 只出现一次的数字 II ② 130. 数字范围…...
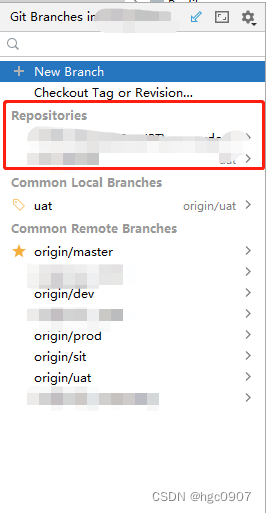
IDEA 多个git仓库项目放一个窗口
1、多个项目先通过新建module或者CtrlAltShiftS 添加module引入 2、重点是右下角有时候git 分支视图只有一个module的Repositories。这时候需要去设置把多个git仓库添加到同一个窗口才能方便提交代码。 3、如果Directory Mappings已经有相关项目配置,但是灰色的&…...
)
全球变暖(蓝桥杯,acwing每日一题)
题目描述: 你有一张某海域 NN 像素的照片,”.”表示海洋、”#”表示陆地,如下所示: ....... .##.... .##.... ....##. ..####. ...###. .......其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿,例如上图就…...

多数据源 - dynamic-datasource | 集成 Quartz 及 ShardingJDBC
文章目录 集成 Quartz引入 quartz-starter配置数据源参数创建任务配置 Quartz 实际使用的数据源方式一: 自定义 SchedulerFactoryBeanCustomizer方式二: 使用@QuartzDataSource来指明quartz数据源集成 ShardingJDBC项目引入 shardingsphere 依赖分别配置shardingjdbc和多数据…...

四连杆机构运动学仿真 | 【Matlab源码+理论公式文本】| 曲柄滑块 | 曲柄摇杆 | 机械连杆
【程序简介】💻🔍 本程序通过matlab实现了四连杆机构的运动学仿真编程,动态展现了四连杆机构的运动动画,同时给出了角位移、角速度和角加速度的时程曲线,除了程序本身,还提供了机构运动学公式推导文档&…...

Lightroom Classic 2024 for mac 中文激活:强大的图像后期处理软件
对于追求极致画面效果的摄影师来说,Lightroom Classic 2024无疑是Mac平台上的一款必备软件。它凭借其强大的功能和出色的性能,赢得了众多摄影师的青睐。 软件下载:Lightroom Classic 2024 for mac 中文激活版下载 在Lightroom Classic 2024中…...

程序员下班以后做什么副业合适?
我就是一个最普通的网络安全工程师,出道快10年了,不出意外地遭遇到瓶颈期,但是凭技术在各大平台挖漏洞副业,硬是妥妥扛过来了。 因为对于程序员来讲,这是个试错成本很低、事半功倍的选择。编程技能是一种强大生产力&a…...
HSE化工应急安全生产管理平台:衢州某巨大型化工企业的成功应用
在化工行业中,安全生产一直是至关重要的议题。为了提高生产安全性、降低成本并提升企业形象,衢州某巨大型化工企业引入了HSE化工应急安全生产管理平台,取得了显著的改善和获益。 该平台的核心功能包括风险管理和应急预案制定。通过对化工生产…...

塑料工厂5G智能制造数字孪生可视化平台,推进塑料行业数字化转型
塑料工厂5G智能制造数字孪生可视化平台,推进塑料行业数字化转型。塑料制造行业作为重要的工业领域,亟需借助这一平台实现产业升级与转型,以适应市场的变化和提高生产效率。传统的塑料制造过程往往存在生产效率低下、资源浪费、环境污染等问题…...
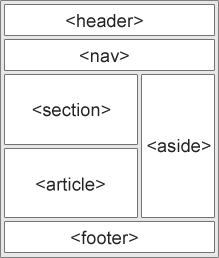
HTML万字学习总结
html文本标签特殊符号图片音频与视频超链接表单列表表格语义标签(布局) html文本标签 标签简介<html></html>根目录<head></head>规定文档相关的配置信息(元数据<body></body>元素表示文档的内容<meta></meta>表示…...

Linux网络编程: 以太网帧Frame/ARP/RARP详解
一、TCP/IP五层模型 物理层(Physical Layer):物理层是最底层,负责传输比特流(bitstream)以及物理介质的传输方式。它定义了如何在物理媒介上传输原始的比特流,例如通过电缆、光纤或无线传输等。…...

【SpringCloud微服务实战09】Elasticsearch 搜索引擎
一、Elasticsearch 安装 1、Docker安装ES #创建一个网络 docker network create es-net#拉取ES镜像(这里使用7.17.18版本) docker pull elasticsearch:7.17.18#新建一个目录存放es数据 mkdir es cd es#docker运行 单机启动es docker run -d \--name es \-e "ES_JAVA_O…...

Leetcode 31. 删除无效的括号
心路历程: 一开始看到有点懵,后来发现有点像按照一定规则穷举所有可能情况,想到了排列组合问题,再结合问题长度不固定,无法用已知个for循环表示,从而想到了回溯。这个题相当于需要在一定规则下枚举。 按照…...
首页效果炫酷的wordpress免费主题模板
视频背景免费WP主题 简洁大气的视频背景wordpress主题,找大视频背景的主题可以看看这个。 https://www.wpniu.com/themes/193.html 红色全屏大图WP主题 非常经典的一款免费wordpress主题,红色全屏大图满足多行业使用。 https://www.wpniu.com/themes…...

网络安全的几个关键领域
网络安全是一个复杂且多维度的领域,涵盖了多个关键领域,涉及到信息保护、网络防护、应用安全、用户教育以及物理安全等多个方面。这些关键领域相互交织,共同构成了网络安全这一宏大且细致入微的领域。 今天德迅云安全就分享下网络安全的几个…...

Vue 计算属性和监视属性
Vue 计算属性和监视属性 computed computed 计算属性 规则: 用已有的属性计算不存在的属性默认调用一次get()只有值不发生改变的时候才可以使用简写(函数);值发生改变 使用对象式写法,才可以配置set()方法底层原理使…...

【Python】反编译PyInstaller打包的exe
查看exe基本信息 需要反编译的exe 查看exe文件的打包工具,查看exe信息的软件叫Detect It Easy(查壳工具) 由图我们可以看出当前选中的exe文件是由名叫PyInstaller的打包工具打包好的exe 反编译 exe反编译工具:pyinstxtractor.py 使用方法 python py…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
