Leetcode 31. 删除无效的括号

心路历程:
一开始看到有点懵,后来发现有点像按照一定规则穷举所有可能情况,想到了排列组合问题,再结合问题长度不固定,无法用已知个for循环表示,从而想到了回溯。这个题相当于需要在一定规则下枚举。
按照回溯的模板,递归循环是整个字符串s,for循环是候选集合。候选集合为第i个元素 “选” 或者 “不选” ,按照这个思路,其实就已经可以把所有可能组成的情况给遍历到,然后再从所有结果里搜集满足条件的即可。
这道题在回溯问题里很有代表性,考察了很多点,包括怎么对排列问题进行建模(选or不选)、如何判断满足括号条件(栈)、如何剪枝。一开始把问题想简单了,导致写完之后花了很长时间解决未通过的案例,这里面还是有一些细节需要考虑的,比如任何回溯都得在递归函数调用结束后“恢复现场”。
注意的点:
1、回溯算法在记录path时一定要记得copy
2、回溯函数中任何递归调用后都得恢复路径,比如这个问题里遇到字母时,虽然形成的树只有一个分支,但是返回后也得恢复path才行;当时第一次想这个问题以为单分支不用恢复路径导致de了半天bug。还是需要理解回溯是遍历边这个概念。
3、剪枝的判断直接返回就行,把剪枝的部分当作不需要记录path的终止条件即可。
4、每个节点候选集合都有空字符串和括号两个选择,需要遍历,没法贪婪地认为有括号选括号,因为需要考虑所有的组合。
5、注意题目中找的是删除最少括号后的所有可能组合,也就是最长的合法解,并且不能包含重复元素。
感悟:
1、算法题主要考察两类能力:一是对问题进行建模的能力;二是逻辑条件的想全能力。很多时候知道问题大概怎么做,但是具体想各种情况时还是会漏掉一些情况或者想错一些情况。
2、回溯问题debug可以从打印路径和候选集合的角度寻找错误。
3、很多算法中循环的建模思路都可以按照’选‘or’不选‘ 或者 ’选哪个‘的思路考虑,尤其在回溯、递归、动态规划等问题上,可以建模为决策问题。这一点其实和DRL在求解组合优化问题时的两类动作建模思路是一致的。
解法:
这道题有两个思路:思路一:剪枝+选择后序有可能形成最长路径;解法二:剪枝+找到所有的+判断满足条件的最长的。第二个可能更清晰,不过由于刚做完括号的题所以按照第一个思路写的AC解:
class Solution:def removeInvalidParentheses(self, s: str) -> List[str]:from collections import Counterpath = []res = []n = len(s)kuohaos = ['(', ')']mystack = Mystack()maxlen = 0def dfs(i): # i代表遍历字符串的第i个元素# nonlocal s, n, res, path, mystack # 这一行可有可无nonlocal maxlen # 这一行必须有# 剪枝:把一些不可能更长的去掉;if (n - len(path)) + len(''.join(path)) < maxlen:returnif i == n:string = ''.join(path.copy())maxlen = max(maxlen, len(string))res.append(string)returnif s[i] not in kuohaos:path.append(s[i])dfs(i+1)path.pop() # 这块也得回溯!!!!!!!else:candidate = [""]# 看第i个括号能不能选即可if s[i] == '(': # 后面)的数量大于等于栈长+1就可以选c = Counter(s[i+1:] + ')') # +1防止为空# print(mystack.sk, c[')'], mystack.len())if c[')'] - 1 >= mystack.len() + 1: candidate.append("(")elif s[i] == ')': # 栈里有左括号if mystack.len() > 0:candidate.append(')')else:assert False, s[i]for each in candidate:# print(each, path, i)path.append(each) # path 怎么会这么长?# 维护一下栈if each != "":mystack.append(each)dfs(i+1)path.pop()if each != "":mystack.pop(each)dfs(0)# 返回res里最长的lengths = [len(eve) for eve in res]res = [eve for eve in res if len(eve) == max(lengths)]return list(set(res)) # 需要去重class Mystack:def __init__(self):from collections import dequeself.sk = deque()def pop(self, ele):if ele == '(':self.sk.pop()elif ele == ')':self.sk.append('(')else:assert False, eledef append(self, ele):if ele == '(':self.sk.append('(')elif ele == ')':assert len(self.sk) != 0self.sk.pop()else:assert False, eledef len(self):return len(self.sk)相关文章:

Leetcode 31. 删除无效的括号
心路历程: 一开始看到有点懵,后来发现有点像按照一定规则穷举所有可能情况,想到了排列组合问题,再结合问题长度不固定,无法用已知个for循环表示,从而想到了回溯。这个题相当于需要在一定规则下枚举。 按照…...
首页效果炫酷的wordpress免费主题模板
视频背景免费WP主题 简洁大气的视频背景wordpress主题,找大视频背景的主题可以看看这个。 https://www.wpniu.com/themes/193.html 红色全屏大图WP主题 非常经典的一款免费wordpress主题,红色全屏大图满足多行业使用。 https://www.wpniu.com/themes…...

网络安全的几个关键领域
网络安全是一个复杂且多维度的领域,涵盖了多个关键领域,涉及到信息保护、网络防护、应用安全、用户教育以及物理安全等多个方面。这些关键领域相互交织,共同构成了网络安全这一宏大且细致入微的领域。 今天德迅云安全就分享下网络安全的几个…...

Vue 计算属性和监视属性
Vue 计算属性和监视属性 computed computed 计算属性 规则: 用已有的属性计算不存在的属性默认调用一次get()只有值不发生改变的时候才可以使用简写(函数);值发生改变 使用对象式写法,才可以配置set()方法底层原理使…...

【Python】反编译PyInstaller打包的exe
查看exe基本信息 需要反编译的exe 查看exe文件的打包工具,查看exe信息的软件叫Detect It Easy(查壳工具) 由图我们可以看出当前选中的exe文件是由名叫PyInstaller的打包工具打包好的exe 反编译 exe反编译工具:pyinstxtractor.py 使用方法 python py…...

【数据结构】哈希表与哈希桶
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》《算法》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.概念 2.哈希冲突…...

幼儿教育管理系统|基于jsp 技术+ Mysql+Java的幼儿教育管理系统设计与实现(可运行源码+数据库+设计文档)
推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含java,ssm,springboot的平台设计与实现项目系统开发资源(可…...

【赠书第21期】游戏力:竞技游戏设计实战教程
文章目录 前言 1 竞技游戏设计的核心要素 1.1 游戏机制 1.2 角色与技能 1.3 地图与环境 2 竞技游戏设计的策略与方法 2.1 以玩家为中心 2.2 不断迭代与优化 2.3 营造竞技氛围与社区文化 3 实战案例分析 4 结语 5 推荐图书 6 粉丝福利 前言 在数字化时代的浪潮中&…...

基于VMware虚拟机安装MacOS BigSur系统
这周用VMWare搞了个MacOS虚拟机,也算是完成初中高中时候的梦想了吧~~(那时候我的电脑配置还很拉跨,带不动虚拟机)~~ 写一篇博客记录一下,当然这也是yonagi04.github.io建站的第一篇新博客 准备工作(VMWare…...
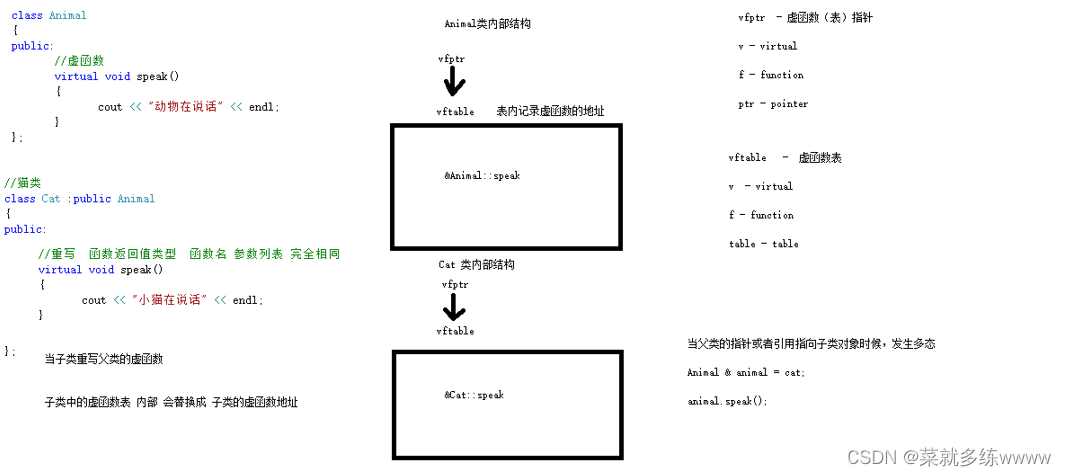
C++特性三:多态的基本语法及原理剖析
一、多态的基本语法 多态分为两类 静态多态: 函数重载 和 运算符重载属于静态多态,复用函数名 动态多态: 派生类和虚函数实现运行时多态 静态多态和动态多态区别: 静态多态的函数地址早绑定 - 编译阶段确定函数地址 动态多态的函数地址晚绑定 - 运…...

Windows下的TCP/IP实例
1.注意事项 windows下winsock.h/winsock2.h linux下sys/socket.h 不同平台头文件不一样 #include <winsock.h> 或者 #include <winsock2.h> 2. 安装minGW 目标是在 Windows 环境下提供类似于 Unix/Linux 环境下的开发工具,使开发者能够轻松地在 Wind…...
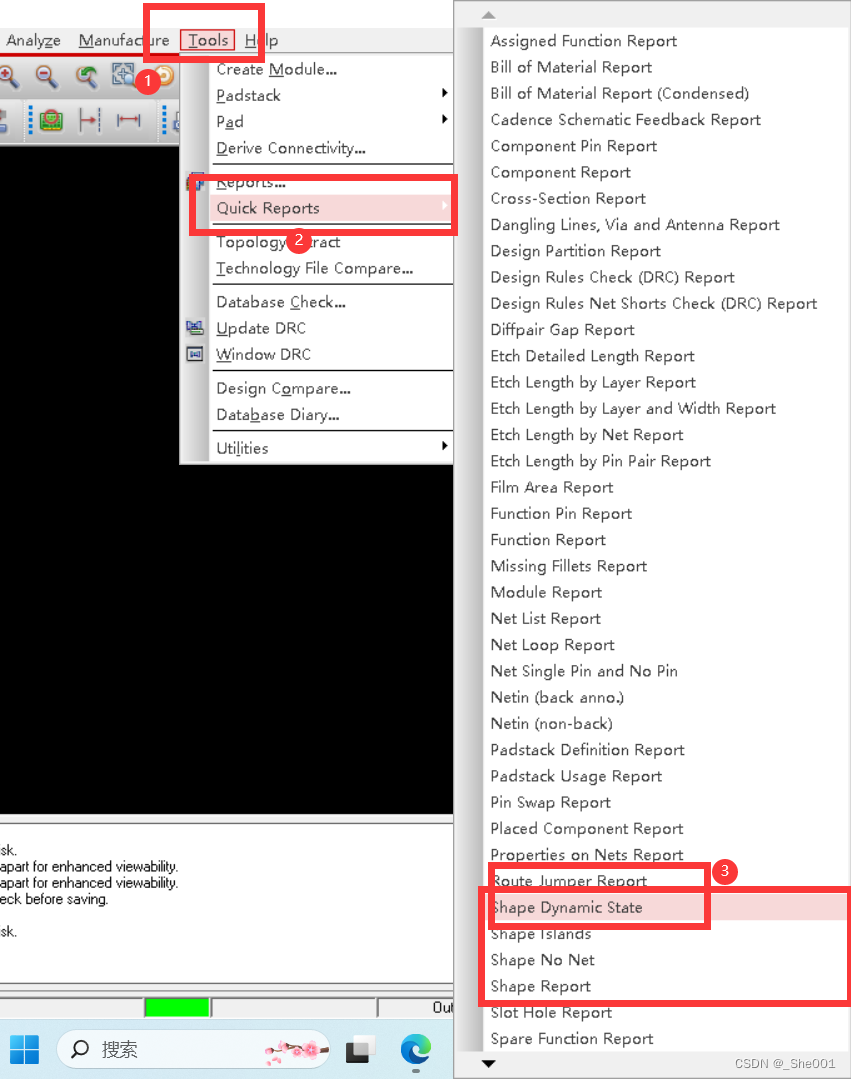
硬件学习件Cadence day15 allegro 查看state 后发现有网络未连接怎么办, shape 有问题怎么办,
1. 当我们查看 state 有问题怎么解决 1. 有问题的图片 2.解决办法: A.网络和节点有问题 如下图所示,点开下面这个窗口进行下面操作,能简单的网络未连接问题。 如下图所示,能进一步解决更难得网络节点未连接问题 如下图所示&#x…...

nginx 中 user 配置的作用
在 Nginx 配置文件中,user 指令用于指定 Nginx 运行时所使用的用户和用户组。默认情况下,Nginx 会以 nobody 用户的身份运行(即使使用 root 用户运行nginx进程, nginx运行过程中线程的用户还是用的nobody),这是一个低权限用户,专门…...
)
愚人节礼物(C++)
这不愚人节 快到了吗?身为顶级程序员,不用c编写愚人节礼物那心里是很不舒服的,所以,趁着愚人节到来之际,下面分享一种坑朋友的c代码: 内容包含一些敏感词,如果对你产生了影响或伤害,…...

Lua 学习
参照 注释 -- 这是单行注释--[[这是多行注释--]]if语句 if true thenprint(true) endif else语句 nil是false if nil thenprint("nil被当作true处理") elseprint("nil被当作false处理") end运算符 % 取余 ^ 乘幂 A10,A^2100 // 整除运算符࿰…...

YOLOv7 | 添加GSConv,VoVGSCSP等多种卷积,有效提升目标检测效果,代码改进(超详细)
⭐欢迎大家订阅我的专栏一起学习⭐ 🚀🚀🚀订阅专栏,更新及时查看不迷路🚀🚀🚀 YOLOv5涨点专栏:http://t.csdnimg.cn/QdCj6 YOLOv7专栏: http://t.csdnimg.cn/dy…...
『运维心得』BPC-EPM-AddIn专家看过来
目录 系统版本问题 安装顺序问题 framework问题 vstor_redis问题 dll问题 一个小彩蛋 总结 最近在搞BPC,安装Office所需的EPM-AddIn的过程中,碰到了一些奇怪的问题。 查了BPC专家提供的安装说明文档,文档里要么没有提到我们碰到的问题…...

论文浅尝 | GPT-RE:基于大语言模型针对关系抽取的上下文学习
笔记整理:张廉臣,东南大学硕士,研究方向为自然语言处理、信息抽取 链接:https://arxiv.org/pdf/2305.02105.pdf 1、动机 在很多自然语言处理任务中,上下文学习的性能已经媲美甚至超过了全资源微调的方法。但是…...
)
Rust语言:告诉编译器允许存在未使用的代码(Rust保留未使用的实现)
Rust告诉编译器允许存在未使用的代码(Rust保留未使用的实现) Rust的Lint工具clippy clippy是一个Rust的Lint工具,旨在帮助开发者发现并改进代码中的潜在问题。它提供了许多静态代码分析的规则和建议,以提高代码质量和可读性。其中就包括检查未使用的代…...

Winform数据绑定
简介# 在C#中提起控件绑定数据,大部分人首先想到的是WPF,其实Winform也支持控件和数据的绑定。 Winform中的数据绑定按控件类型可以分为以下几种: 简单控件绑定列表控件绑定表格控件绑定 绑定基类# 绑定数据类必须实现INotifyPropertyChanged…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
