栈队列数组试题(四)——数组和特殊矩阵
01.对特殊矩阵采用压缩存储的主要目的是( D ).
A.表达变得简单 B.对矩阵元素的存取变得简单
C.去掉矩阵中的多余元素 D.减少不必要的存储空间
解析:特殊矩阵中含有很多相同元素或零元素,所以采用压缩存储,以节省存储空间
02.对n阶对称矩阵压缩存储时,需要表长为( C )的顺序表。
A. n/2 B. n×n/2 C. n(n+1)/2 D. n(n-1)/2
解析:对称矩阵只需存储上三角或下三角部分(含对角线),元素个数为n+(n-1)+(n-2)+...+1=n(n+1)/2
03.有一个nn的对称矩阵A,将其下三角部分按行存放在一维数组B中,而A[0][0]存
放于B[0]中,则第i+1行的对角元素A[i][i]存放于B中的( A )处。
A. (i+ 3)i/2 B. (i+1)i/2 C. (2n- i+1)i/2 D. (2n- i- 1)i/2
解析:矩阵的最小下标为0,数组下标也是从0开始,矩阵按行优先存在数组中,可以采用特殊代值法,如A[1][1]的下标为2,代入后只有A满足条件
04.在二维数组A中,假设每个数组元素的长度为3个存储单元,行下标i为0~8,列下标
j为0~9,从首地址SA开始连续存放。在这种情况下,元素A[8][5]的起始地址为()
A.SA+141 B. SA+144 C. SA+222 D. SA+255
解析:二维数组计算地址(按行优先顺序)的公式为 LOC(i,j)=LOC(0,0)+(i*m+j)*L
LOC(0,0)是SA,是数组存放的首地址;L=3是每个数组元素的长度,m=9-0+1是数组的列数
所以LOC(8,5)=SA+(8*10+5)*3=SA+255;
05.二维数组A按行优先存储,其中每个元素占1个存储单元。若A[1][1]的存储地址为
420,A[3][3]的存储地址为446,则A[5][5]的存储地址为( A ).
A. 472 B.471 C. 458 D. 457
解析:该二维数组按行优先存储,且A[3][3]的存储地址为446,所以A[3] [1]的存储地址为444,又A[1][1]的存储地址为420,显然A[1][1]和A[3][1]正好相差2行,所以该矩阵的列数为12。而A[5][3]和A[3] [3]正好相差2行,A[5][5]和A[5][3]又相差2个元素,所以A[5][5]的存储地址是446+24*2=472
06.将三角矩阵即数组A[1..100][1..100]按行优先存入一维数组B[1..298]中,数组
中元素A[66] [65]在数组B中的位置k为( B ).
A.198 B.195 C. 197 D.196
解析:对于三对角矩阵,将A[1..n][1..n]压缩至B[1...3n-2]时,ai,j与bk的对应关系为k=2i+j-2,则A[66][65]=2*66+65-2=195
07.若将n阶上三角矩阵A按列优先级压缩存放在一维数组B[ 1...n (n+1)/2+1]中,则存
放到B[ k]中的非零元素ai,j (1≤i,j≤n)的下标i、j与k的对应关系是( C ).
A. i(i+1)/2+j B. i(i- 1)/2 +j-1 C. j(j-1)/2+i D. j(j-1)/2+ i-1
解析:按列优先存储,所以ai,j前面有j-1列,共有1+2+3+...+j-1=j(j-2)/2个元素,元素ai,j在第j列上是第i个元素,数组B的下标是从1开始,因此k=j(j-1)/2+i.
08.若将n阶下三角矩阵A按列优先顺序压缩存放在一维数组B[ 1...n (n+1)/2+1]中,则
存放到B[k]中的非零元素ai,j(1≤i,j≤n)的下标i, j与k的对应关系是( B ).
A. (j-1)(2n-j+1)/2+i- j B. (j-1)(2n-j+2)/2 +i-j+1
C. (j-1)(2n-j+2)/2+i-j D. (j-1) (2n-j+1)/2+i-j-1
解析:按列优先存储,所以元素ai,j前有j-1列,共有n+(n-1)+..+(n-j+2)=(j-1)(2n-j+2)/2个元素,元素ai,j是第j列上的第i个元素,数组下标从1开始,k=(j-1)(2n-j+2)/2+i-j+1
09.稀疏矩阵采用压缩存储后的缺点主要是( B )。
A.无法判断矩阵的行列数 B.丧失随机存取的特性
C.无法由行、列值查找某个矩阵元素 D.使矩阵元素之间的逻辑关系更复杂
解析:稀疏矩阵通常采用三元组来压缩存储,存储矩阵元素的行列下标和相应的值,因此不能根据矩阵元素的行列下标快速定位矩阵元素,失去了随机存取的特性。
10.下列关于矩阵的说法中,正确的是(B ).
I、在n ( n>3)阶三对角矩阵中,每行都有3个非零元
Ⅱ、稀疏矩阵的特点是矩阵中的元素较少
A.仅Ⅰ B.仅Ⅱ C.Ⅰ和Ⅱ D.无正确项
解析:三对角矩阵中,第1行和最后一行只有2个非零元,其余各行均有3个非零元,稀疏矩阵的特点是矩阵中非零元的个数较少
11.【2016统考真题】有一个100阶的三对角矩阵M,其元素mi,j ( 1≤i, j≤100)按行优先
依次压缩存入下标从0开始的一维数组N中。元素m30,30在N中的下标是( B ).
A. 86 B. 87 C. 88 D.89
解析:三对角矩阵第一行有两个元素,剩下的在元素m30,30所在行之前的28行(注意下标1<=i,j<=100)中,每行都有3个元素,而m30,30之前只有一个元素m30,29,所以m30,30在数组N中的下标是2+28*3+2-1=87
12.【2017统考真题】适用于压缩存储稀疏矩阵的两种存储结构是( A )
A.三元组表和十字链表 B.三元组表和邻接矩阵
C.十字链表和二叉链表 D.邻接矩阵和十字链表
解析:三元组表的结点存储了行(row)、列(col)、值(value)三种信息,是主要用来存储稀疏矩阵的一种数据结构。十字链表将行单链表和列单链表结合起来存储稀疏矩阵。邻接矩阵空间复杂度达O(n^2),不适合于存储稀疏矩阵。二叉链表又名左孩子右兄弟表示法,可用于表示树或森林。
13.【2018统考真题】设有一个12×12阶对称矩阵M,将其上三角部分的元素mi,j( 1≤i≤j≤12 )
按行优先存入C语言的一维数组N中,元素m6,6在N中的下标是( A ).
A. 50 B. 51 C. 55 D. 66
解析:M的下标从0开始,第一个元素m1,1对应存入N0,第一行12个元素,第二行11个,第三行10个,第四行9个,第五行8个,所以m6,6是第12+11+10+9+8+1=51个元素,下标为50
14.【2020统考真题】将一个10×10阶对称矩阵M的上三角部分的元素mi,j ( 1≤i≤j≤10)
按列优先存入C语言的一维数组N中,元素m7,2在N中的下标是(C )。
A. 15 B.16 C.22 D.23
解析:M的下标从0开始,按列优先存储,第一列1个元素,第二列2个,,,第6列6个,所以m7,2是第1+2+3+4+5+6+2=23个元素 所以下标为22
15.【2021统考真题】二维数组A按行优先方式存储,每个元素占用1个存储单元。若元素
A[0][0]的存储地址是100,A[3][3]的存储地址是220,则元素A[5][5]的存储地址是( B )。
A. 295 B.300 C. 301 D.306
解析:二维数组按行优先存储,每个元素占1个存储单元,有A[0][0]和A[3][3]的存储地址可知A[3][3]是第121个元素,假设二维数组每行有n个元素,则n*3+4=121,n=39,所以元素A[5][5]的存储地址为100+39*5+6-1=300
16.【2023统考真题】若采用三元组表存储结构存储稀疏矩阵M,则除三元组表外,下列数
据中还需要保存的是( A ).
I. M的行数 Ⅱ. M中包含非零元素的行数
Ⅲ. M的列数 IV. M中包含非零元素的列数
A.仅Ⅰ、Ⅲ B.仅I、IV C.仅II、IV D. Ⅰ、Ⅱ、Ⅲ、IV
解析:用三元组表存储结构存储稀疏矩阵M时,每个非零元素都由三元组(行标、列标、关键字值)组成。但是,仅通过三元组表中的元素无法判断稀疏矩阵M的大小,因此还要保存M的行数和列数。此外,还可以保存M的非零元素个数。如果两个稀疏矩阵的三元组表是相同的,若不保存行数和列数,则无法判断两个稀疏矩阵的大小。
相关文章:
——数组和特殊矩阵)
栈队列数组试题(四)——数组和特殊矩阵
01.对特殊矩阵采用压缩存储的主要目的是( D ). A.表达变得简单 B.对矩阵元素的存取变得简单 C.去掉矩阵中的多余元素 D.减少不必要的存储空间解析:特殊矩阵中含有很多相同元素…...
数据结构的概念大合集01(含数据结构的基本定义,算法及其描述)
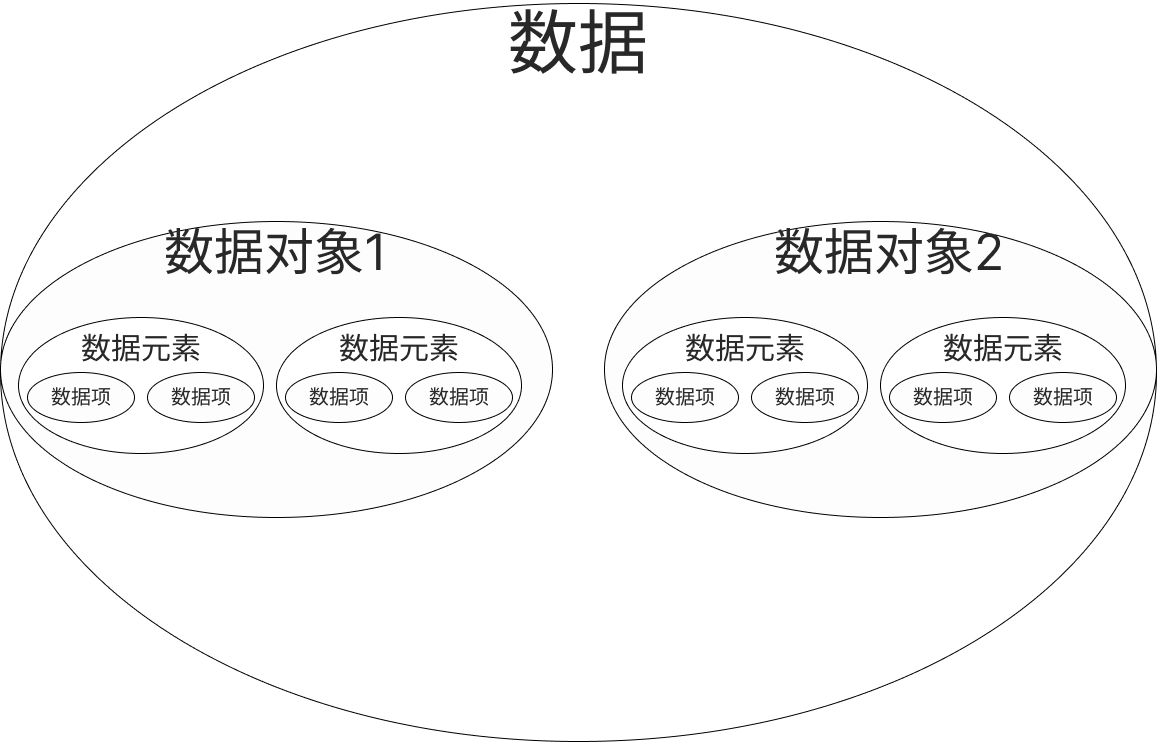
概念大合集01 1、数据结构基础的定义2、数据结构2.1 数据元素之间关系的集合2.2数据结构的三要素2.2.1数据的逻辑结构2.2.2数据的存储(物理)结构2.2.3数据的运算 3、数据类型4、抽象数据类型类型(ADT)5、算法及其描述5.1算法的5个…...
.NET高级面试指南专题十七【 策略模式模式介绍,允许在运行时选择算法的行为】
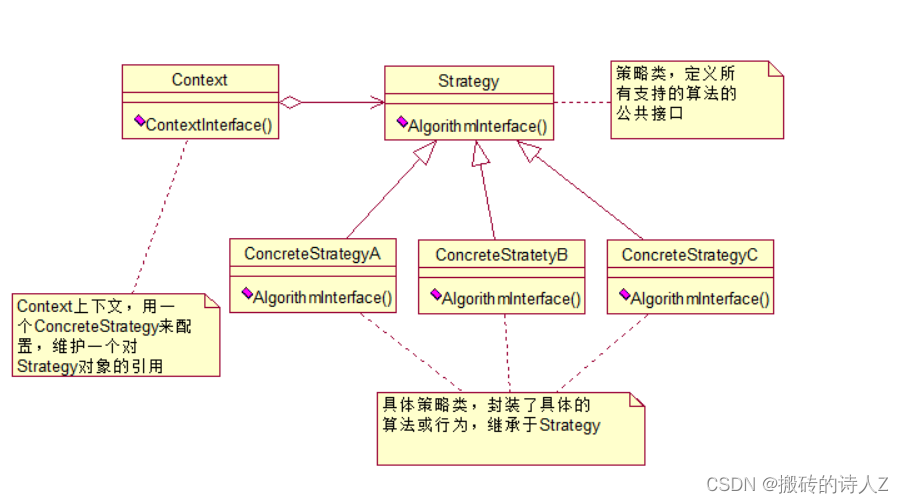
介绍: 策略模式是一种行为设计模式,它允许在运行时选择算法的行为。它定义了一系列算法,将每个算法封装到一个对象中,并使它们可以互相替换。这使得算法可独立于使用它的客户端变化。 原理: 策略接口(Strat…...

突飞猛进,智能饮品机器人如何助力实体经济?
近日,财务部公布了2024年第一季度及全年财报。数据显示,连锁品牌增长速度惊人,这其中不得不提到智能饮品机器人的使用,为不同的品牌门店拼速度、抢点位立下了不小的功劳,那么智能饮品机器人到底如何助力各门店…...
AI:150-基于深度学习的医学数据挖掘与病症关联发现
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带关键代码,详细讲解供大家学习,希望…...

c语言:最大公约数
最大公约数 任务描述 最大公约数(也称最大公因数、最大公因子),指两个或多个整数共有约数中最大的一个。 编程输入两个正整数,输出它们的最大公约数。 输入示例 36 24输出示例 12代码 方法1:辗转相除法 #inclu…...

12 对称加密AES和非对称加密RSA
文章目录 一、对称加密算法AES1. AES简介2. AES代码 二、非对称加密RSA1. RSA简介2. 生成公钥私钥3. RSA代码 一、对称加密算法AES 1. AES简介 对称加密算法AES是目前广泛使用的一种加密技术,它采用相同的密钥来进行数据的加密和解密。 AES的优点 高效性&#x…...
:计算属性、监视属性、二者的区别)
Vue2(二):计算属性、监视属性、二者的区别
一、计算属性 1. 使用插值语法和methods拼接姓名 如果样式要求不多的话这样写没问题,如下代码是截取我输入的姓的前三个字母 <div id"root">姓:<input type"text" v-moudel"firstName">名:<…...
CTF题型 SSTI(2) Flask-SSTI典型题巩固
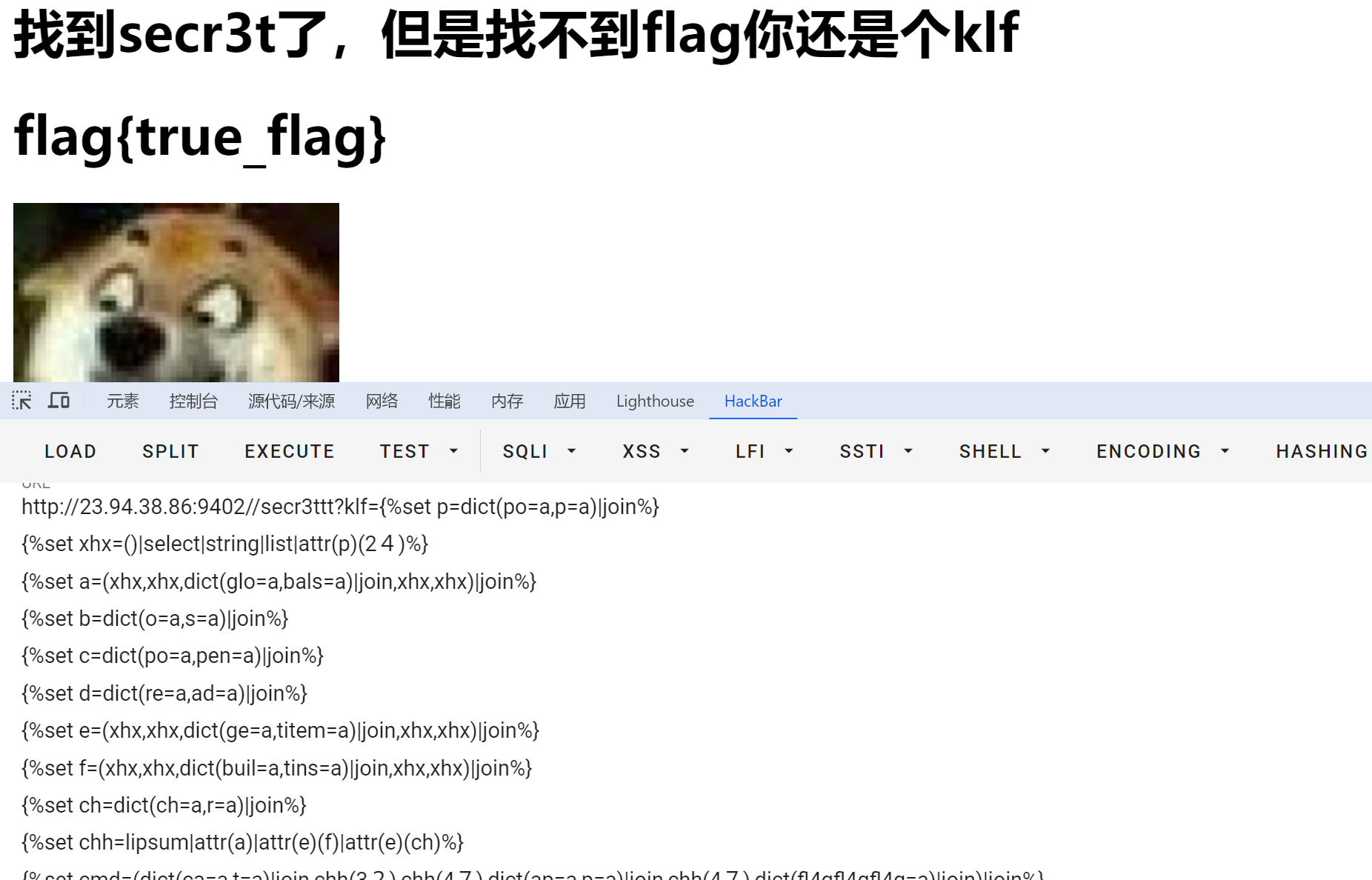
CTF题型 SSTI(2) Flask-SSTI典型题巩固 文章目录 CTF题型 SSTI(2) Flask-SSTI典型题巩固前记1.klf__sstiSSTI_Fuzz字典(网上收集自己补充) 2.klf_2数字问题如何解决了?|count |length都被禁? 3.klf_3 前记 从基础到自己构造paylo…...

计算机设计大赛 题目: 基于深度学习的疲劳驾驶检测 深度学习
文章目录 0 前言1 课题背景2 实现目标3 当前市面上疲劳驾驶检测的方法4 相关数据集5 基于头部姿态的驾驶疲劳检测5.1 如何确定疲劳状态5.2 算法步骤5.3 打瞌睡判断 6 基于CNN与SVM的疲劳检测方法6.1 网络结构6.2 疲劳图像分类训练6.3 训练结果 7 最后 0 前言 🔥 优…...
小字辈[天梯赛]
文章目录 题目描述思路AC代码 题目描述 思路 深度优先搜索 具体流程 1.读入每个人的祖先,标记辈分最高的老祖宗对应的下标pos 2.从pos开始dfs,每次判断当前遍历的深度,如果>原来的深度,更新,并将存储最小辈分的数组…...

Linux常用操作命令、端口、防火墙、磁盘与内存
目录 1.Linux常用操作命令 1.1 基本命令 1.2 高级命令 2.Linux防火墙 2.1 iptables 2.2 firewalld 3.Linux端口号 3.1 netstat(查看网络连接) 3.2 lsof(查找占用端口的进程) 3.3 ps(查看进程服务路径&#x…...
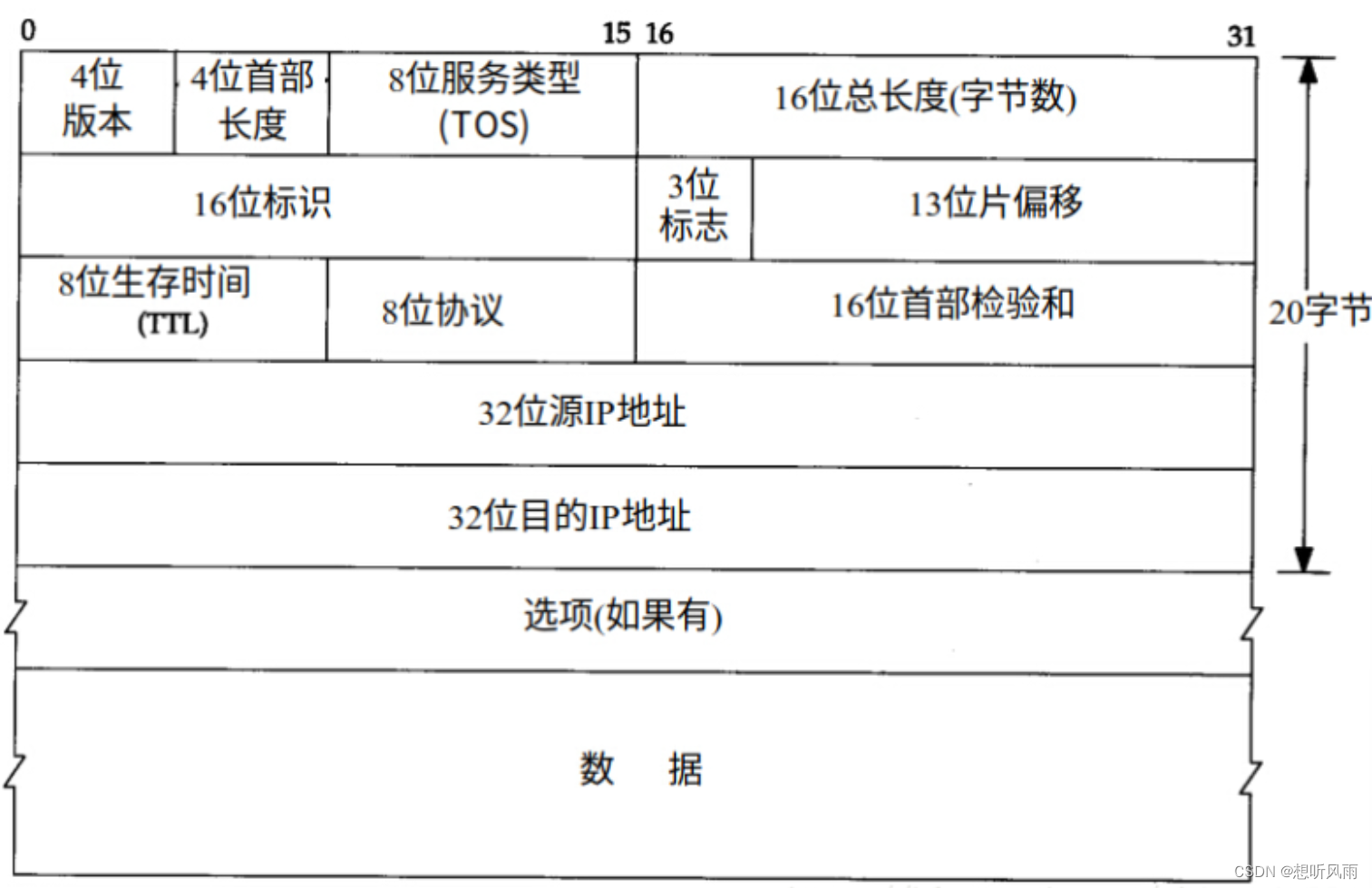
<JavaEE> 了解网络层协议 -- IP协议
目录 初识IP协议 什么是IP协议? IP协议中的基础概念 IP协议格式 图示 4bit版本号(version) 4bit头部长度(headerlength) 8bit服务类型(TypeOfService) 16bit总长度(total l…...
【安全类书籍-2】Web渗透测试:使用Kali Linux
目录 内容简介 作用 下载地址 内容简介 书籍的主要内容是指导读者如何运用Kali Linux这一专业的渗透测试平台对Web应用程序进行全面的安全测试。作者们从攻击者的视角出发,详细阐述了渗透测试的基本概念和技术,以及如何配置Kali Linux以适应渗透测试需求。书中不仅教授读者…...
ubuntu10.04 apache2.2开启tls1.2的支持,使现代的edge和firefox浏览器能正常访问https
最近发现自己ubuntu10.04服务器上的apache https无法通过win11上的edge和firefox浏览器访问,但xp下的ie6和ie8没有问题。 firefox的错误提示为“此网站可能不支持TLS 1.2协议,而这是Firefox支持的最低版本”。 经过检查发现: IE6访问https所需的版本是SS…...
算法学习(持续更新中)
学习视频:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解(马士兵)_哔哩哔哩_bilibili 时间复杂度 一个操…...

蓝桥杯 2023 省B 飞机降落
首先,这题要求的数据量比较少,我们可以考虑考虑暴力解法。 这题可能难在很多情况的考虑,比如说: 现在时间是10,有个飞机20才到,我们是可以干等10分钟。 #include <iostream> #include <…...
基于python的变配电室运行状态评估与预警系统flask-django-nodejs-php
近年来,随着我国工业化、城镇化步伐的不断加快,城市配电网络取得令人瞩目的发展成果。变配电室是供配电系统的核心,在供配电系统中占有特殊的重要地位[1]。变配电室电气设备运行状态和环境信息缺乏必要的监测评估预警手段,如有一日遭遇突发情…...
,右键单击展示操作菜单,可编辑单元格高亮展示)
el-table左键双击单元格编辑内容(输入框输入计算公式可直接得出结果),右键单击展示操作菜单,可编辑单元格高亮展示
vue2点击左侧的树节点(el-tree)定位到对应右侧树形表格(el-table)的位置,树形表格懒加载 表格代码 <el-table ref"singleTable" :data"detailsList" highlight-current-row"" row-key"detailId"…...

实现HBase表和RDB表的转化(附Java源码资源)
实现HBase表和RDB表的转化 一、引入 转化为HBase表的三大来源:RDB Table、Client API、Files 如何构造通用性的代码模板实现向HBase表的转换,是一个值得考虑的问题。这篇文章着重讲解RDB表向HBase表的转换。 首先,我们需要分别构造rdb和hba…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
