滴滴基于 Clickhouse 构建新一代日志存储系统
滴滴基于 Clickhouse 构建新一代日志存储系统
ClickHouse 是2016年开源的用于实时数据分析的一款高性能列式分布式数据库,支持向量化计算引擎、多核并行计算、高压缩比等功能,在分析型数据库中单表查询速度是最快的。2020年开始在滴滴内部大规模地推广和应用,服务网约车和日志检索等核心平台和业务。本文主要介绍滴滴日志检索场景从 ES 迁移到 CK 的技术探索。
背景
此前,滴滴日志主要存储于 ES 中。然而**,ES 的分词、倒排和正排等功能导致其写入吞吐量存在明显瓶颈**。此外,ES 需要存储原始文本、倒排索引和正排索引,这增加了存储成本,并对内存有较高要求。随着滴滴数据量的不断增长,ES 的性能已无法满足当前需求。
在追求降低成本和提高效率的背景下,我们开始寻求新的存储解决方案。经过研究,我们决定采用 CK 作为滴滴内部日志的存储支持。据了解,京东、携程、B站等多家公司在业界的实践中也在尝试用 CK 构建日志存储系统。
挑战
面临的挑战主要来自下面三个方面:
- 数据量大:每天会产生 PB 级别的日志数据,存储系统需要稳定地支撑 PB 级数据的实时写入和存储。
- 查询场景多:在一个时间段内的等值查询、模糊查询及排序场景等,查询需要扫描的数据量较大且查询都需要在秒级返回。
- QPS 高:在 PB 级的数据量下,对 Trace 查询同时要满足高 QPS 的要求。
为什么选 Clickhouse
相关文章:

滴滴基于 Clickhouse 构建新一代日志存储系统
滴滴基于 Clickhouse 构建新一代日志存储系统 ClickHouse 是2016年开源的用于实时数据分析的一款高性能列式分布式数据库,支持向量化计算引擎、多核并行计算、高压缩比等功能,在分析型数据库中单表查询速度是最快的。2020年开始在滴滴内部大规模地推广和应用,服务网约车和日…...

虚拟主机去除index.php目录地址
复制代码到NGINX设置 虚拟主机去除index.php目录地址-复制代码-NGINX设置 location / { if (!-e $request_filename) { rewrite ^(.*)$ /index.php?s/$1 last; break; } } location ~ /\.ht { deny all; }...

JD商品详情原数据 API 返回值说明
一、应用场景 商品详情原数据API的应用场景广泛而多样。具体来说,它可以被用于以下方面: 1、电商平台数据分析:电商平台可以通过商品详情原数据API提取商品销售数据、质量评分、评论和反馈等信息,从而帮助用户更好地理解市场和竞…...

python日常刷题(一)
前言:本文记录2024年3月11日至2024年3月19日牛客网所做的基础题目(错题本): 🎬个人简介:努力学习ing 📋本专栏:python日常刷题 🎀CSDN主页:愚润求学 文章目录…...

Python 利用pandas和mysql-connector获取Excel数据写入到MySQL数据库
如何将Excel数据插入到MySQL数据库中 在实际应用中,我们可能需要将Excel表格中的数据导入到MySQL数据库中,以便于进行进一步的数据分析和处理。本文将介绍如何使用Python将Excel表格中的数据插入到MySQL数据库中。 导入必要的库 首先,我们…...

Stable Diffusion训练图片时,简陋的数据处理
0 图片从命名 如果有强迫症,看到似乎乱码的命名会不舒服,那么就批量从命名 import osdef rename_files_in_directory(directory, key_word, new_suffix):i 1for filename in os.listdir(directory):new_file key_word str(i).zfill(3) new_suffixsou…...

如何在ubuntu 18.04中升级python 3.6到3.7
在ubuntu下安装python 3.7有两种方法: 1,通过使用Deadsnakes PPA中的标准apt工具(本文暂时只介绍这种方法) 2,从源代码进行构建。 前提条件: 需要以root用户或具有sudo访问权限的用户身份登录才能在Ubuntu系统上安装软件包。 方法一:使用apt工具安装…...

python爬虫基础实验:通过DBLP数据库获取数据挖掘顶会KDD在2023年的论文收录和相关作者信息
Task1 读取网站主页整个页面的 html 内容并解码为文本串(可使用urllib.request的相应方法),将其以UTF-8编码格式写入page.txt文件。 Code1 import urllib.requestwith urllib.request.urlopen(https://dblp.dagstuhl.de/db/conf/kdd/kdd202…...
简单记录一次帮维修手机经历(Vivo x9)
简介 手边有一台朋友亲戚之前坏掉的Vivo X9手机, 一直说要我帮忙修理一下, 我一直是拒绝的, 因为搞程序的不等于维修的(会电脑不等于维修电器),不知道这种思路如何根深蒂固的,不过好吧ÿ…...

ap聚类是什么
AP聚类(Affinity Propagation clustering)是一种聚类算法,它基于数据点之间的相似度进行聚类。AP聚类算法无需预先指定簇的数量,而是根据数据点之间的相似性动态地确定簇的个数和分配情况。 AP聚类的核心思想是通过迭代计算数据点…...
C数据类型(C语言)---变量的类型决定了什么?
目录 数据类型(Data Type) 变量的类型决定了什么? (1)不同类型数据占用的内存大小不同 如何计算变量或类型占内存的大小 (2)不同数据类型的表数范围不同 (3)不同类型…...

axios、axios二次封装、api解耦
import axios from axios// 环境的切换切换测试与生产环境 if (process.env.NODE_ENV development) { axios.defaults.baseURL /api; } else if (process.env.NODE_ENV debug) { axios.defaults.baseURL ; } else if (process.env.NODE_ENV production) { axios.…...

HTML 特殊元素:展示PDF、展示JSON 数据
<pre> 标签 (preformatted text) <pre> 标签用来表示预格式化的文本内容 在页面数据展示时,后端返回了一段未经处理的JSON 数据,将这段数据在页面正常展示,让可读性更高。 {/"project": {/ "title": "…...

算法·动态规划Dynamic Programming
很多人听到动态规划或者什么dp数组了,或者是做到一道关于动态规划的题目时,就会有一种他很难且不好解决的恐惧心理,但是如果我们从基础的题目开始深入挖掘动规思想,在后边遇到动态规划的难题时就迎难而解了。 其实不然ÿ…...

鸿蒙Harmony应用开发—ArkTS-转场动画(共享元素转场)
当路由进行切换时,可以通过设置组件的 sharedTransition 属性将该元素标记为共享元素并设置对应的共享元素转场动效。 说明: 从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 属性 名称参数参数描述…...

【C语言】循环语句(语句使用建议)
文章目录 **while循环****while循环的实践****补充:if语句与while语句区别****for循环(使用频率最高)****for循环的实践****while循环和for循环的对比****Do-while循环****break和continue语句****循环的嵌套****goto语句(不常用)****循环语句的效率(来自于高质量的C/C编程书籍…...

Spring Data访问Elasticsearch----响应式Reactive存储库
Spring Data访问Elasticsearch----响应式Reactive存储库 一、用法二、配置 Reactive Elasticsearch存储库支持建立在存储库中解释的核心存储库支持之上,利用由 Reactive REST客户端执行的 Reactive Elasticsearch Operations提供的操作。 Spring Data Elasticsear…...

堆排序(c语言)
文章目录 前言一.什么是堆二.向下调整算法三.堆排序的创建总结 前言 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于&#x…...

开源IT自动化运维工具Ansible解析
Ansible 是一款开源的 IT 自动化工具,用于简化应用程序部署、配置管理、持续集成、基础设施即代码(Infrastructure as Code, IaC)和服务编排。它由 Michael DeHaan 创建,并在2012年首次发布,到2015年被红帽公司&#x…...
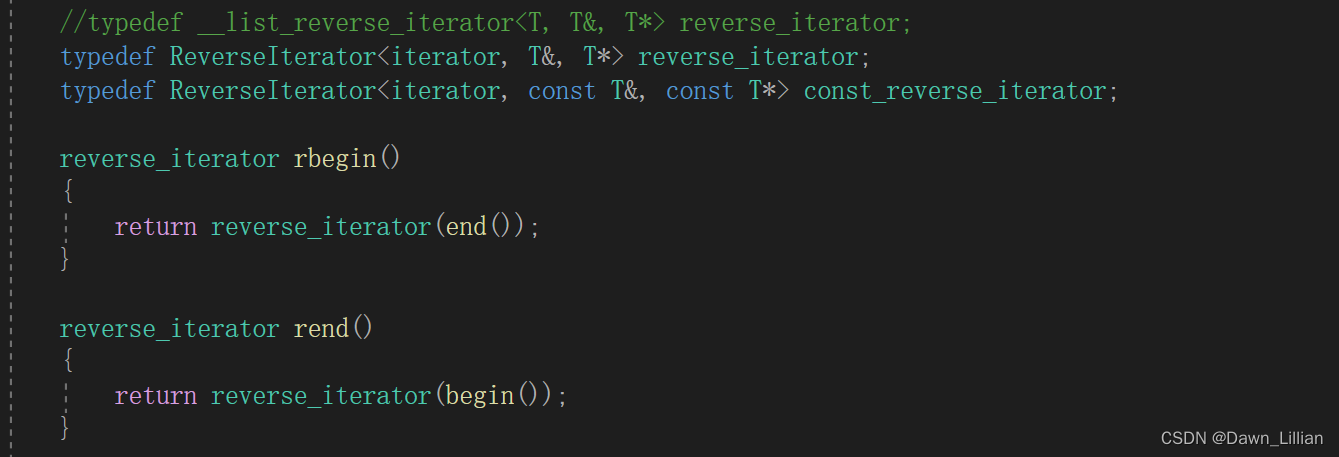
【C++】仿函数优先级队列反向迭代器
目录 一、优先级队列 1、priority_queue 的介绍 2、priority_queue 的使用 3、 priority_queue 的模拟实现 1)priority_queue()/priority_queue(first, last) 2)push(x) 3)pop() 4&#…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
