3703. 括号的匹配 北京师范大学考研上机真题 栈的思想
在算术表达式中,除了加、减、乘、除等运算外,往往还有括号。
包括有大括号 {},中括号 [],小括号 (),尖括号 <> 等。
对于每一对括号,必须先左边括号,然后右边括号;如果有多个括号,则每种类型的左括号和右括号的个数必须相等;对于多重括号的情形,按运算规则,从外到内的括号嵌套顺序为:大括号->中括号->小括号->尖括号,另外相同的括号可以嵌套。
例如,{[()]},{(())},{{}} 为一个合法的表达式,而 ([{}]),{([])},[{<>}] 都是非法的。
输入格式
第一行包含整数 n,表示共有 n个表达式需要判断。
接下来 n 行,每行包含一个括号表达式。
输出格式
每行输出一个表达式的判断结果。
如果合法输出 YES,否则输出 NO。
数据范围
1≤n≤100
表达式长度不超过 100100。
输入样例:
5 {[(<>)]} [()] <>()[]{} [{}] {()}
输出样例:
解释
YES YES YES NO YES
#include <bits/stdc++.h>using namespace std;unordered_map<char, int> mp{{'{',1},{'[',2},{'(',3},{'<',4},{'}',5},{']',6},{')',7},{'>',8}};char g[110];int main()
{int n;cin >> n;while(n --){memset(g, 0, sizeof g);cin >> g;int len = strlen(g);stack<char> stack;for (int i = len - 1; i >= 0; i --){if(stack.empty()) stack.push(g[i]);else if(mp[stack.top()] > mp[g[i]] && mp[g[i]] > 4) break; else if(mp[stack.top()] - mp[g[i]] == 4 ) stack.pop();else stack.push(g[i]);}if(stack.empty()) puts("YES");else puts("NO");}return 0;
}
相关文章:

3703. 括号的匹配 北京师范大学考研上机真题 栈的思想
在算术表达式中,除了加、减、乘、除等运算外,往往还有括号。 包括有大括号 {},中括号 [],小括号 (),尖括号 <> 等。 对于每一对括号,必须先左边括号,然后右边括号;如果有多个…...
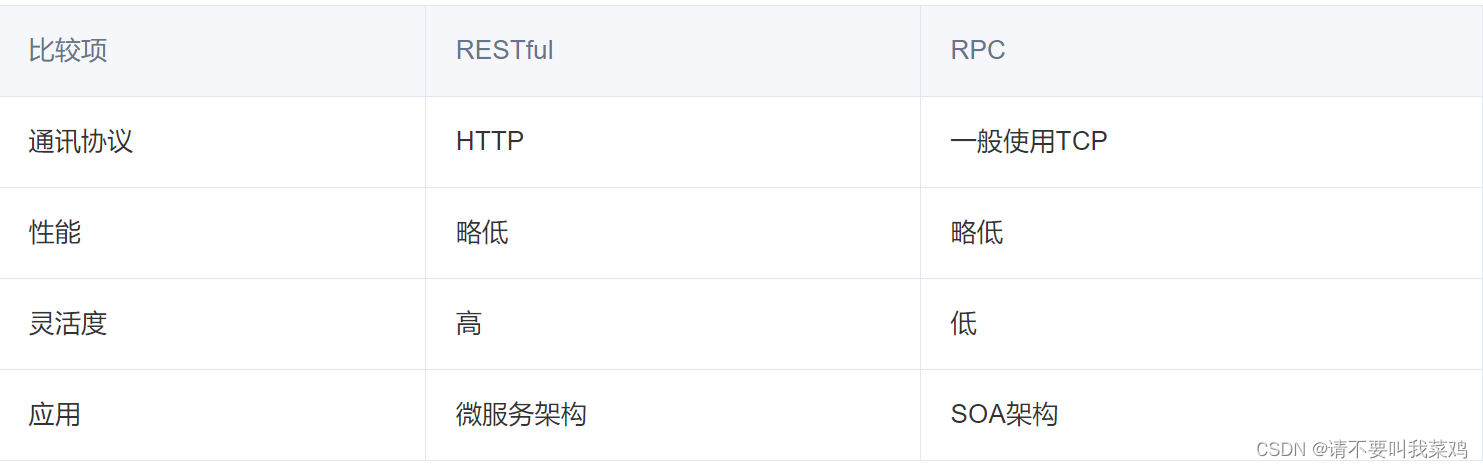
SpringCloud中的@EnableDiscoceryClient和@EnableFeignClients注解的作用解析、RPC远程过程调用
目录 EnableDiscoveryClient 服务发现的核心概念 服务注册中心 EnableDiscoveryClient注解的作用 服务心跳健康检查 使用示例 EnableFeignClients Feign简介 EnableFeignClients注解的作用 RPC(Remote Procedure Call) 参考链接 Spring Cloud…...
文件复制,文件夹复制)
关于安卓文件复制的杂谈(一)文件复制,文件夹复制
背景 一些很基础的东西,往往用起来,找起来,乱七八糟,所以特此记录 环境 win10,jdk8,as4 备注 不考虑安卓沙箱机制,这里讲解的是思路,示例中,是以应用内部目录进行测试 开发 把一个文件&a…...

Lucene查询语法,适用于 ELk Kibana 查询
Lucene查询语法,适用于 ELk Kibana 查询 Elasticsearch 构建在 Lucene 之上,过滤器语法和 Lucene 相同。本语法可用于 Kibana 界面的检索和 Grafana 看板对接 ES 的检索规则。 Kibana 上的检索语法Grafana 上的检索语法 全文搜索 在搜索栏输入login&…...

蓝桥杯2023年第十四届省赛真题-阶乘求和
一、题目 【问题描述】 令 S 1 ! 2 ! 3 ! . . . 202320232023 ! S 1! 2! 3! ... 202320232023!S1!2!3!...202320232023!,求 S SS 的末尾 9 位数字。 提示:答案首位不为 0。 【答案提交】 这是一道结果填空的题,你只需要算出结果后…...
多租户平台前端存储结构的选择
下图来源于cookie、localStorage 和 sessionStorage的区别及应用实例 既然localstorage无有效期,关闭浏览器还存在,那么用来存储用户的身份信息并不是太合适,先看一下B站中localstorage都存在了啥,原来把我搜索的记录都存在了下来…...
)
C++11 新特性:常量表达式 constexpr(下)
接上篇文章,继续说说常量表达式 constexpr 在模板编程中的使用场景。 constexpr 用于模板编程 在模板编程中,constexpr 的应用非常广泛,主要是因为它能够在编译时进行计算,这对于模板元编程、编译时断言、模板特化选择等场合尤为…...
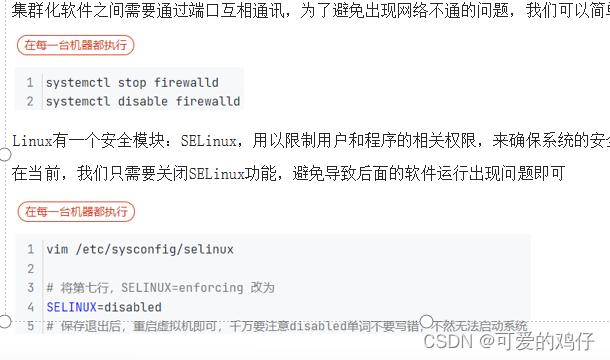
大数据开发--02.环境准备
一.准备三台linux虚拟机 1.分别取名node1,node2,node3 2.配置静态ip 这里以node1为例,配置静态ip地址,其他node2.node3一样 配置完成之后别忘记 systemctl restart network 3.在各自的/etc/hosts文件中编辑三个Ip地址 三台都要配置, 4.然…...

选择word中的表格VBA
打开开发工具 选择Visual Basic插入代码 Sub 选择word中的表格() Dim t As Table an MsgBox("即将选择选区内所有表格,若无选区,则选择全文表格。", vbYesNo, "提示") If an - 6 Then Exit Sub Set rg IIf(Selection.Type wdSel…...
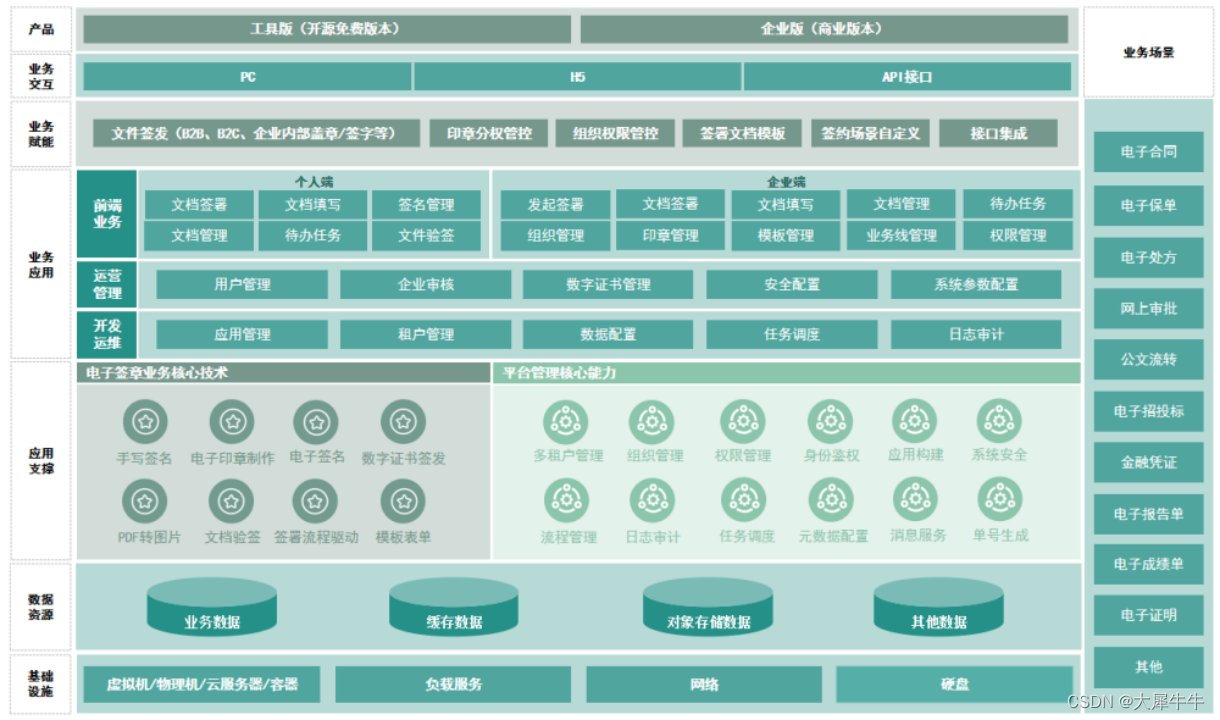
开放签开源电子签章白皮书-简版
开放签开源电子签章白皮书-简版 一、摘要: 开放签电子签章团队源自于电子合同SaaS公司,立志于通过开源、开放的模式,结合团队十多年的行业经验,将电子签章产品更简单、更低门槛的推广到各行各业中。让电子签章应用更简单&#x…...
uniapp、vue2.6、H5,利用腾讯TRTC,快速跑通1v1视频功能
多人视频聊天室搭建,官网已有相关demo和案例,需要快速搭建多人聊天室直接进入以下网站: 实时音视频 Web & H5 (Vue2/Vue3)-视频通话(含 UI)-文档中心-腾讯云说明:https://cloud.tencent.com/document/…...

Spring Data访问Elasticsearch----查询方法
Spring Data访问Elasticsearch----查询方法 一、查询lookup策略1.1 声明的查询 二、创建查询三、方法返回类型四、使用Query注解 一、查询lookup策略 Elasticsearch模块支持所有基本的查询构建功能,如字符串查询、native搜索查询、基于条件的查询和从方法名派生的查…...
PyTorch 深度学习(GPT 重译)(四)
第二部分:从现实世界的图像中学习:肺癌的早期检测 第 2 部分的结构与第 1 部分不同;它几乎是一本书中的一本书。我们将以几章的篇幅深入探讨一个单一用例,从第 1 部分学到的基本构建模块开始,构建一个比我们迄今为止看…...
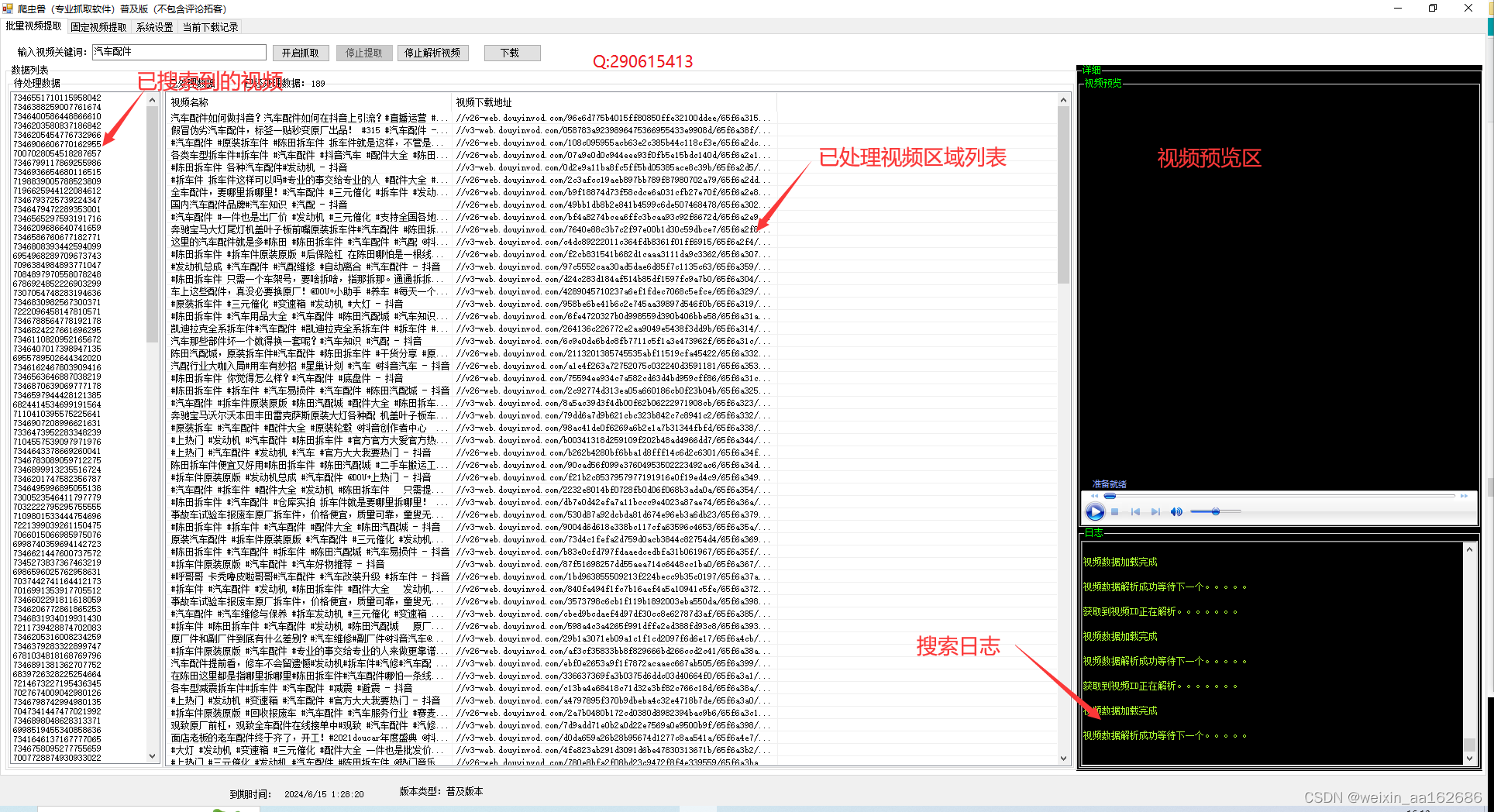
视频无水印批量下载软件|抖音视频提取工具
视频无水印批量下载软件 在当今社交媒体充斥着大量优质视频内容的时代,很多用户都希望能够轻松下载自己喜爱的视频进行收藏或分享。为了满足用户的需求,我们特别推出了一款专业的视频无水印批量下载软件,让您可以方便快捷地获取喜爱的视频内容…...

【linux】环境基础|开发工具|gcc|yum|vim|gdb|make|git
目录 编辑 Linux 软件包管理器 yum 软件包: 操作: 拓展:lrzsz简介 Linux开发工具 Linux编辑器-vim使用 vim 的基本概念 命令模式 插入模式 底行模式 vim 命令模式的操作指令 vim 底行模式的操作命令 Linux编译器-gcc/g使用 功能 格…...

小程序中实现轮播图左向堆叠
1、效果图: 轮播图左向堆叠 2、封装的组件: my-swiper.wxml <view><view class"tower-swiper" bindtouchend"TowerEnd"><view class"tower-item" wx:for"{{swiperList}}" wx:key"index&q…...
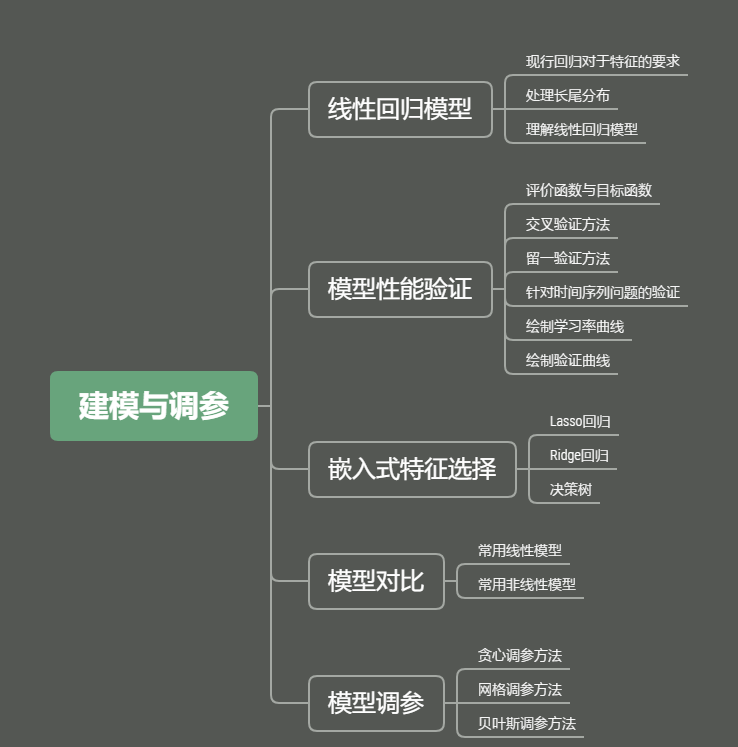
零基础入门数据挖掘系列之「建模调参」
摘要:对于数据挖掘项目,本文将学习如何建模调参?从简单的模型开始,如何去建立一个模型;如何进行交叉验证;如何调节参数优化等。 建模调参:特征工程也好,数据清洗也罢,都是…...
如何在Mac中删除照片?这里有详细步骤
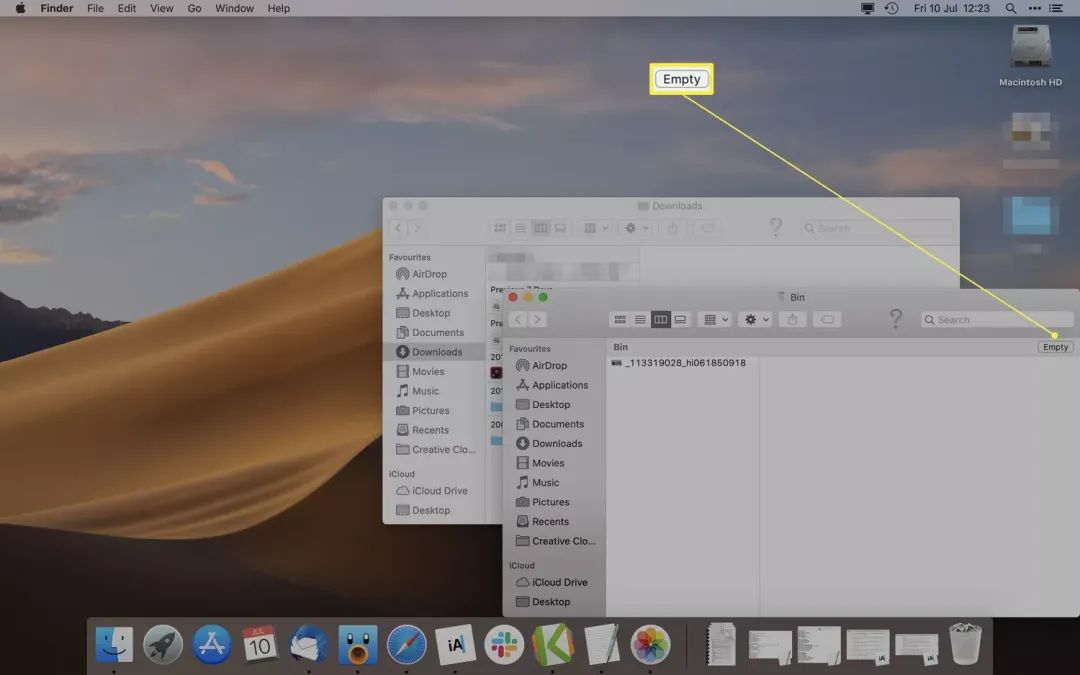
前言 本文介绍如何从Mac中删除照片,以释放硬盘空间或更好地组织文件和文件夹。 如何使用废纸篓删除Mac上的图片 在Mac上删除图片的最简单方法之一是使用废纸篓功能。学习只需几秒钟。下面是如何删除单个图片以及如何在Mac上删除多个图片,以及一些关键和有用的提示,以使该…...
Qt笔记 事件处理_鼠标事件
什么是事件? 点击鼠标左键,双击鼠标左键,鼠标来回移动,按下键盘按钮,这些都是事件。 那么事件的响应机制是什么样的呢? 首先main函数中有一个QApplication,其作用是创建一个应用程序对象&…...

【Vue】三、使用ElementUI实现图片上传
目录 一、前端代码实现 二、后端代码实现 三、调试效果实现 一、前端代码实现 废话不多说直接上代码 <el-form-item prop"image" label"上传图片" v-model"form.image"><el-upload:action"http://localhost:8…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
