蓝桥杯刷题|03普及-真题
[蓝桥杯 2017 省 B] k 倍区间
题目描述
给定一个长度为 N 的数列,,
,⋯
,如果其中一段连续的子序列
,
,⋯
(i≤j) 之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
输入格式
第一行包含两个整数 N 和 K(1≤N,K≤)。
以下 N 行每行包含一个整数 (1≤
≤
)。
输出格式
输出一个整数,代表 K 倍区间的数目。
输入输出样例
输入 #1
5 2 1 2 3 4 5
输出 #1 6
说明/提示
时限 2 秒, 256M。蓝桥杯 2017 年第八届
对于这个题,先用了暴力枚举来解题,发现只能过两个样例,其他的都超时了,之后看了题解,他们用了前缀和思想,下面我就整理前缀和相关概念和解题方法。
前缀和
前缀和是什么?
通俗理解,前缀和就是任意一个元素前面所有元素的和(包括本身);
例如:这有一个数组arr[3]={1,2,3}
如果设定一个数组为此数组的前缀和数组perfix[3]={1,3,6}
前缀和的好处
好处就是减少时间复杂度,例如上面的题,要求一段区间的和,用暴力枚举就会超时。使用前缀和,我们只需要用末尾的前缀和减去初位置的前缀和就可以得到该区间的和了;
我们来举个例子吧。定义一个arr[6]={1,2,3,4,5,6},求这个数组的任意一个区间[i,j]的和
暴力枚举
我们肯定会从第一个元素开始,每次往后+1;然后从第二个元素开始,每次往后+1...;
假设要求[i,j]这个区间的和
for(int t=0;i<t;t++)int num1+=arr[t];for(int m=j;m<=j;m++)int num2+=arr[m];int num=num2-num1;前缀和
定义一个 前缀和数组,从头开始求前缀和之后的前缀和就是前一个前缀和加上当前元素
prefix[0]=arr[0];
for(int n=0;n<arr.size;i++)prefix[n]=prefix[n-1]+arr[n];
int num=predix[j]-prefix[i-1];
prefix[j]-prefix[i-1]=arr[i]+arr[i+1]+...+arr[j];
因为这个题是一维的,我们就先介绍一维前缀和。
K倍区间解题思路
这个题不仅利用了前缀和还要转换思想,要求K的倍数,也就是是说根据前缀和里面的元素的运算得到的结果,只要没有余数就行,为防止数值溢出,我们可以只给前缀和里面存余数就行,余数如果为0,那么就是k的倍数。
因此这个前缀和数组中存的不是和,而是和的余数。具体操作如下:
prefix[0]=arr[0];
for(int n=0;n<arr.size;i++)prefix[n]=(prefix[n-1]+arr[n])/K;第一步可以直接判断prefix数组里面的值是否0,等于0就是K 的倍数。
第二步就是中间子序列的值是否是K的倍数,令这个子序列的左下标为left,令右下标为right,那么子序列的和可以表示为prefix[right]-prefix[left-1],判断是不是K的倍数就是判断这个子序列的和除于K的余数是否为0。
(prefix[right]-prefix[left-1])%K==0
prefix[right]%K-prefix[left-1]%K==0
prefix[right]%K==prefix[left-1]%K
因此只要判断prefix[right]%K==prefix[left-1]%K就行,换个说法就是要找相同的有几个,假如有a个相同,这些相同的两两组合就可以构成一个子序列,也就是高中学的排列组合,我定义一个cnt数组,里面的数就代表i向同的有几个,然后两两组合,也就是
=
最后不要忘了前缀和里面单独余数为0的也是K的倍数,cnt[0]就是余数为0的个数。加上就行。
最后就是注意,记得数据类型定义为long long int
具体代码如下
#include<iostream>
#include<vector>
using namespace std;
long long int n=1e6+10;
int main()
{long long int N,K,num=0,i;cin>>N>>K;vector <long long int>arr(n);//原数组 vector <int>prefix(n);//前缀和数组vector <long long int>cnt(n);for(i=1;i<=N;i++){cin>>arr[i];//数组输入prefix[i]=(prefix[i-1]+arr[i])%K;//前缀和数组 cnt[prefix[i]]++;//统计里面相同的 }for(i=0;i<N;i++){num+=cnt[i]*(cnt[i]-1)/2;//将相同的进行排列组合 }cout<<num+cnt[0];//余数为0的本来就是K的倍数 return 0;} 相关文章:
蓝桥杯刷题|03普及-真题
[蓝桥杯 2017 省 B] k 倍区间 题目描述 给定一个长度为 N 的数列,,,⋯,如果其中一段连续的子序列 ,,⋯ (i≤j) 之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。 你能求出数列中总共有多少个 K 倍区间吗? 输入格式 …...

【动态三维重建】Deformable 3D Gaussians 可变形3D GS用于单目动态场景重建(CVPR 2024)
主页:https://ingra14m.github.io/Deformable-Gaussians/ 代码:https://github.com/ingra14m/Deformable-3D-Gaussians 论文:https://arxiv.org/abs/2309.13101 文章目录 摘要一、前言二、相关工作2.1 动态场景的神经渲染2.2 神经渲染加速 三…...
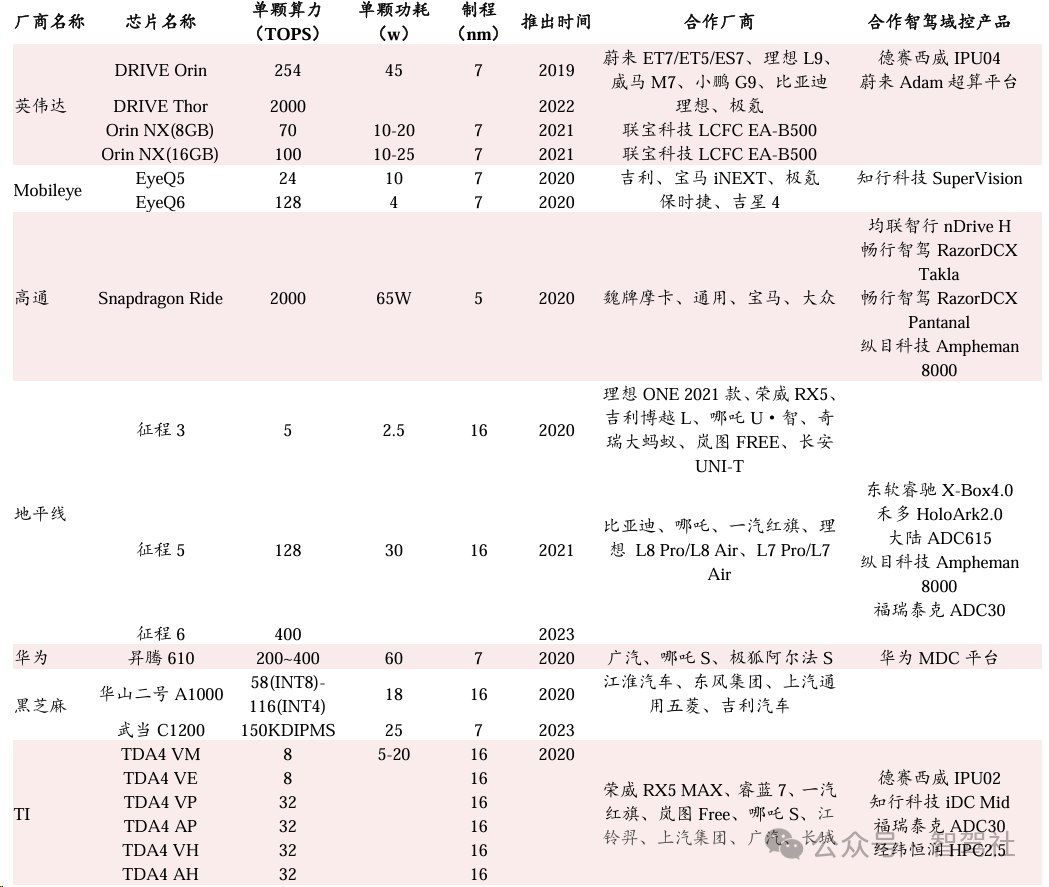
智能驾驶域控制器行业介绍
汽车智能驾驶功能持续高速渗透,带来智能驾驶域控制器市场空间快速增 长。智驾域控制器是智能驾驶决策环节的重要零部件,主要功能为处理感知 信息、进行规划决策等。其核心部件主要为计算芯片,英伟达、地平线等芯 片厂商市场地位突出。随着消费…...

[数据集][目标检测]焊接件表面缺陷检测数据集VOC+YOLO格式2292张10类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):2292 标注数量(xml文件个数):2292 标注数量(txt文件个数):2292 标注…...

微信小程序的页面制作---常用组件及其属性
微信小程序里的组件就是html里的标签,但其组件都自带UI风格和特定的功能效果 一、常用组件 view(视图容器)、text(文本)、button(按钮)、image(图片)、form(…...

什么样的网站不适合使用WordPress?
WordPress作为全球应用最广泛的CMS系统,很好很强大,被从多的网站使用。但是,也不是所有的网站。下面简站WP小编从自己多年WordPress建站经验的角度,给大家讲讲,有哪些网站不适合使用WordPress搭建。 1、功能特别多的功…...
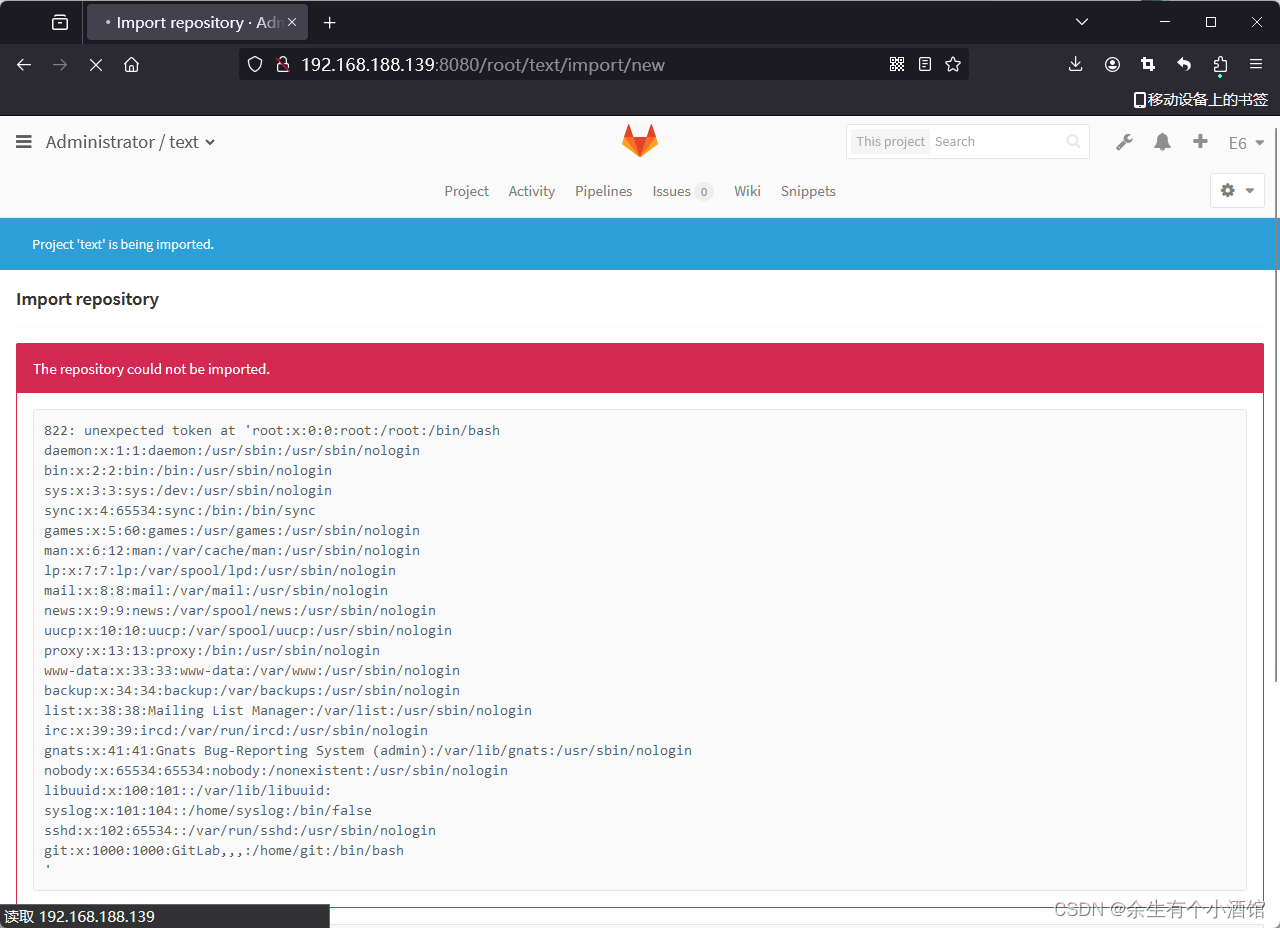
vulhub中GitLab 任意文件读取漏洞复现(CVE-2016-9086)
GitLab是一款Ruby开发的Git项目管理平台。在8.9版本后添加的“导出、导入项目”功能,因为没有处理好压缩包中的软连接,已登录用户可以利用这个功能读取服务器上的任意文件。 环境运行后,访问http://your-ip:8080即可查看GitLab主页࿰…...

【爬虫】web自动化和接口自动化
专栏文章索引:爬虫 目录 一、介绍 二、推荐 1.接口自动化 2.Web自动化 一、介绍 爬虫技术一般可以分为两种类型:接口自动化和web自动化。下面是它们的简要介绍: 1.接口自动化 接口自动化技术的主要目的是通过模拟HTTP请求来实现自动化…...

哔哩哔哩后端Java一面
前言 作者:晓宜 个人简介:互联网大厂Java准入职,阿里云专家博主,csdn后端优质创作者,算法爱好者 最近各大公司的春招和实习招聘都开始了,这里分享下去年面试B站的的一些问题,希望对大家有所帮助…...
Vue.js前端开发零基础教学(二)
目录 前言 2.1 单文件组件 2.2 数据绑定 2.2.2 响应式数据绑定 2.3 指令 2.3.1 内容渲染指令 2.3.2 属性绑定指令 编辑 2.3.3 事件绑定指令 2.3.4 双向数据绑定指令 2.3.5 条件渲染指令 2.3.6 列表渲染指令 2.4 事件对象 2.5 事件修饰符 学习目标&am…...

Bert模型输出:last_hidden_state转换为pooler_output
1. BERT模型的输出 在BERT模型中,last_hidden_state和pooler_output是两个不同的输出。 (1) last_hidden_state: last_hidden_state是指BERT模型中最后一个隐藏层的隐藏状态。它是一个三维张量,其形状为[batch_size, sequence_length, hidden_size]。其…...

Docker Compose 基本语法
services 是顶级节点,也就是你要启动的服务全部放在这里。 MySOL就是我们预期中的一个服务。 mysql8:指的是我们这个服务叫 mysql8. image:我们这个服务里运行的是什么镜像,或者说跑的是什么。这里指定了使用 mysql:8.0.29 这个版本。 command:启动命令&…...

【算法集训】基础算法:贪心
1913. 两个数对之间的最大乘积差 void insertSort(int * a, int n) {for(int i 1; i < n; i) {int temp a[i];int j i - 1;while(j > 0 && temp < a[j]) {a[j 1] a[j];j--;}a[j 1] temp;} }int maxProductDifference(int* nums, int numsSize){insert…...
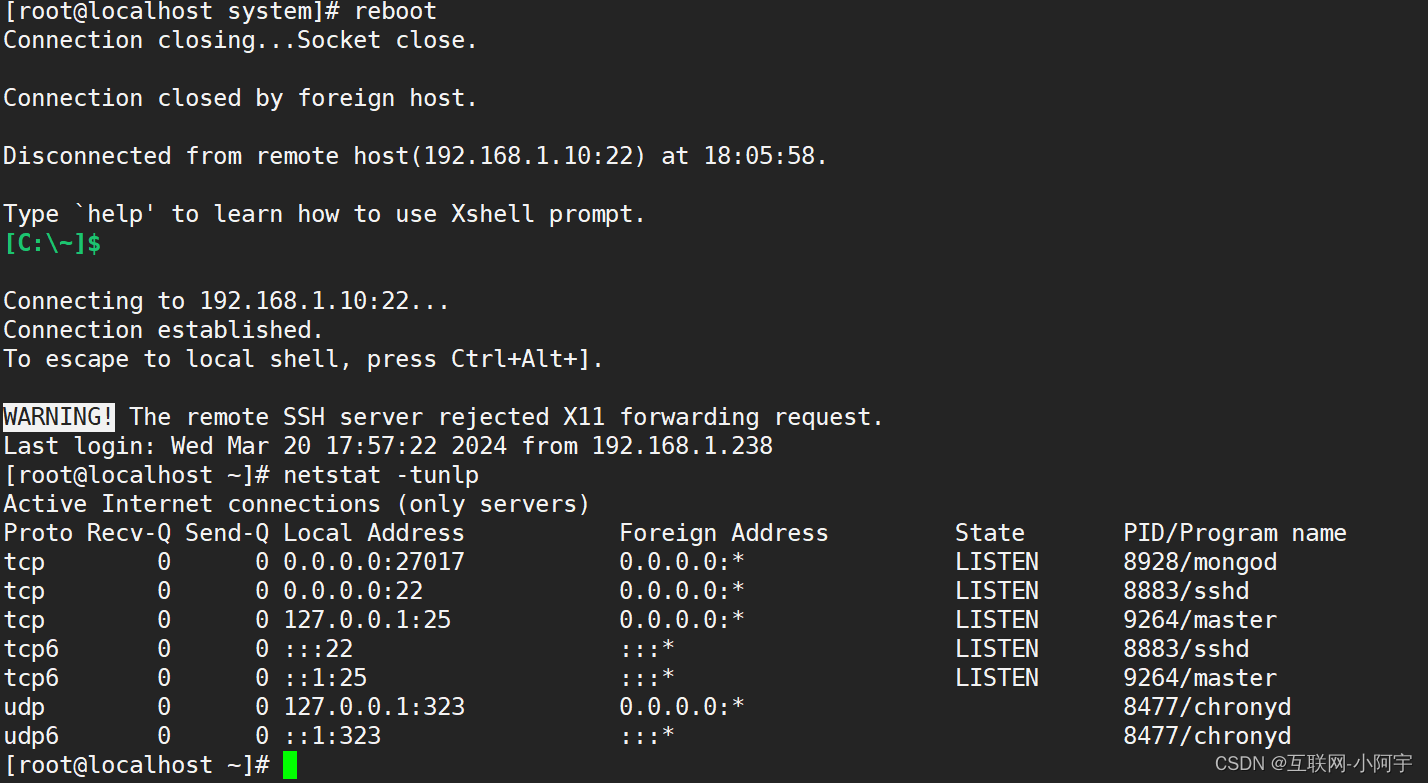
Centos7部署单节点MongoDB(V4.2.25)
🎈 作者:互联网-小啊宇 🎈 简介: CSDN 运维领域创作者、阿里云专家博主。目前从事 Kubernetes运维相关工作,擅长Linux系统运维、开源监控软件维护、Kubernetes容器技术、CI/CD持续集成、自动化运维、开源软件部署维护…...
)
隐私计算笔记(1)
一、可信流通体系 建立数据来源可确认、使用范围可界定、流通过程可追溯、安全风险可防范的数据可流通体系。 二、产生信任的基石 身份可确认利益可依赖能力有预期行为有后果 三、数据流通不可信风险 内循环:在内部循环中,数据持有方在其自身的运维…...

查询方法需要使用事务吗?
当数据库隔离级别是默认的可重复读(Repeatable Read)时,如果查询语句只有一条则不需要事务. 当有多条查询sql语句且需要确保多条sql语句处于同一时间维度时则需要使用事务来确保多条SQL语句处于同一时间节点. 相关知识点 mysql查询当前事务隔…...

剑指offer面试题40 数组中只出现一次的数字
考察点 异或运算,与运算知识点 题目 分析 本题目要求数组中只出现一次的俩个数字,并且要求O(1)时间复杂度和空间复杂度。试想一下如果只有一个数字出现一次,那么针对全部元素做异或运算就可以了,因为相同元素异或为0。现在有俩…...
gitLab server version 13.12.1 is not supported
拉代码的时候,报的这个错,实际上就是因为gitLab 版本太低了,这里不准备升级版本,打算继续使用账号密码来拉取代码 在idea已经安装的插件中,去掉gitlab插件,如下: 之后再拉取代码,就…...

如何在 iPhone 上使用蓝牙鼠标
iPhone 不支持使用传统的鼠标指针。 然而,有一个名为“AssistiveTouch”的功能可以在屏幕上模拟类似光标的指针。 启用它的方法如下: 打开 iPhone 上的“设置”应用程序。转到“辅助功能”。向下滚动并选择“触摸”。点击“辅助触控”。切换开关以打开 …...
matlab simulink 电力系统同步发电机励磁系统的建模与仿真
1、内容简介 略 77-可以交流、咨询、答疑 电力系统同步发电机励磁系统的建模与仿真 建立MATLAB的同步发电机励磁调节系统仿真模型,最后建立了以PID和PSS为励磁控制方式的同步发电机励磁调节系统数学模型,在Simulink环境下进行了仿真,收到…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
