力扣热门算法题 52. N 皇后 II,53. 最大子数组和,54. 螺旋矩阵
52. N 皇后 II,53. 最大子数组和,54. 螺旋矩阵,每题做详细思路梳理,配套Python&Java双语代码, 2024.03.20 可通过leetcode所有测试用例。
目录
52. N 皇后 II
解题思路
完整代码
Python
Java
53. 最大子数组和
解题思路
完整代码
Python
Java
54. 螺旋矩阵
解题思路
完整代码
Python
Java
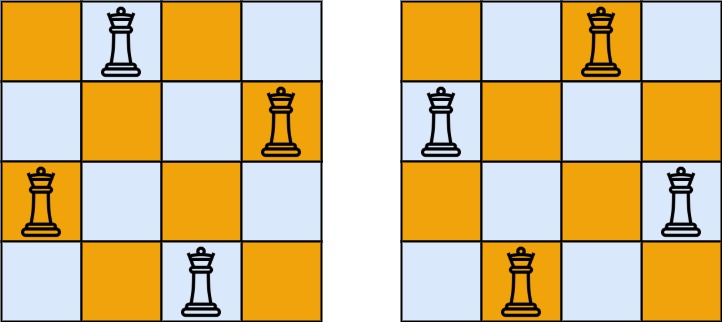
52. N 皇后 II
n 皇后问题 研究的是如何将
n个皇后放置在n × n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回 n 皇后问题 不同的解决方案的数量。示例 1:
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1 输出:1提示:
1 <= n <= 9
解题思路
可以使用回溯法,类似于解决 n 皇后问题摆放方案的方法,但这次我们只需要计算不同解决方案的数量。关键点在于合理地放置皇后,以避免她们相互攻击。
-
初始化数据结构:使用数组或其他数据结构来标记哪些列、对角线(左上到右下和右上到左下)已经被占用。
-
递归回溯:从第一行开始,尝试在每一列放置皇后。对于放置在
(row, col)的皇后,需要标记第col列、(row + col)的左上到右下对角线和(row - col)的右上到左下对角线为占用状态。 -
检查冲突:在尝试放置每个皇后之前,检查当前列和两个对角线是否已经被其他皇后占用。
-
统计解决方案数量:每当成功放置了
n个皇后(即达到了最后一行的下一行),就将解决方案数量加一。 -
回溯:尝试当前行的下一列或回到上一行,撤销当前放置的皇后,并尝试新的位置。
完整代码
Python
class Solution:def totalNQueens(self, n: int) -> int:def backtrack(row = 0, hills = 0, next_row = 0, dales = 0, count = 0):if row == n: # 如果已经放置了 n 个皇后count += 1 # 解决方案数量加一else:# 在所有可用的列中free_columns = columns & ~(hills | next_row | dales)while free_columns:# 选择最右侧的可用列curr_column = - free_columns & free_columns# 放置皇后并去掉当前列free_columns ^= curr_columncount = backtrack(row + 1, (hills | curr_column) << 1, next_row | curr_column, (dales | curr_column) >> 1, count)return count# 初始化可用列columns = (1 << n) - 1return backtrack()Java
public class Solution {private int size;private int count;private void solve(int row, int ld, int rd) {if (row == size) {count++;return;}int pos = size & ~(row | ld | rd);while (pos != 0) {int p = pos & -pos;pos -= p; // 放置皇后并移除当前位置solve(row | p, (ld | p) << 1, (rd | p) >> 1);}}public int totalNQueens(int n) {count = 0;size = (1 << n) - 1;solve(0, 0, 0);return count;}public static void main(String[] args) {Solution solution = new Solution();int n = 4;System.out.println(solution.totalNQueens(n));}
}
53. 最大子数组和
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组
是数组中的一个连续部分。示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1] 输出:1示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
解题思路
我们可以使用一个称为“Kadane算法”的高效方法。Kadane算法通过一次遍历数组来找到最大的连续子数组和。该算法的基本思想是维护一个局部最大和一个全局最大变量,随着数组的遍历,更新这两个变量。
-
初始化两个变量:
currentMax用于追踪当前位置的最大子数组和,globalMax用于记录迄今为止找到的最大子数组和。初始时,两个变量都设置为数组的第一个元素。 -
遍历数组:从数组的第二个元素开始遍历。
-
更新
currentMax:对于每个元素,更新currentMax为当前元素本身和当前元素加上之前的currentMax之间的较大者。这一步骤确保了currentMax总是维护着到当前位置为止的最大子数组和。currentMax = max(nums[i], currentMax + nums[i]) -
更新
globalMax:如果更新后的currentMax大于globalMax,则更新globalMax为currentMax的值。这确保了globalMax总是全局最大子数组和。globalMax = max(globalMax, currentMax) -
返回结果:遍历完成后,
globalMax将包含整个数组的最大子数组和。
完整代码
Python
class Solution:def maxSubArray(self, nums: List[int]) -> int:currentMax = globalMax = nums[0]for num in nums[1:]:currentMax = max(num, currentMax + num)globalMax = max(globalMax, currentMax)return globalMaxJava
public class Solution {public int maxSubArray(int[] nums) {int currentMax = nums[0];int globalMax = nums[0];for (int i = 1; i < nums.length; i++) {currentMax = Math.max(nums[i], currentMax + nums[i]);globalMax = Math.max(globalMax, currentMax);}return globalMax;}public static void main(String[] args) {Solution solution = new Solution();int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};System.out.println(solution.maxSubArray(nums));}
}
54. 螺旋矩阵
给你一个
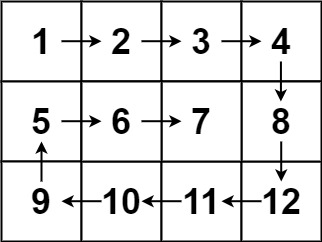
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
解题思路
要按顺时针螺旋顺序返回矩阵中的所有元素,我们可以模拟整个过程,遵循从左到右、从上到下、从右到左、从下到上的顺序,每完成一圈后,缩小遍历的范围。
-
初始化四个方向的边界:
top、bottom、left、right分别代表了上下左右四个方向的边界。初始化时,top = 0,bottom = m-1,left = 0,right = n-1。 -
按顺序遍历矩阵:按照顺时针方向遍历矩阵的外围,然后逐层向内缩小范围,直到遍历完所有元素。具体步骤如下:
a. 从左到右遍历上层元素(
top行),遍历完成后top++。b. 从上到下遍历右侧元素(
right列),遍历完成后right--。c. 如果
top <= bottom,从右到左遍历底层元素(bottom行),遍历完成后bottom--。d. 如果
left <= right,从下到上遍历左侧元素(left列),遍历完成后left++。 -
收集元素:在每个方向上遍历时,将遍历到的元素添加到结果列表中。
-
返回结果:当上述遍历完成后,结果列表中将包含按顺时针螺旋顺序的所有矩阵元素。
完整代码
Python
class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:result = []if not matrix:return resulttop, bottom, left, right = 0, len(matrix) - 1, 0, len(matrix[0]) - 1while left <= right and top <= bottom:# 从左到右for i in range(left, right + 1):result.append(matrix[top][i])top += 1# 从上到下for i in range(top, bottom + 1):result.append(matrix[i][right])right -= 1# 从右到左if top <= bottom:for i in range(right, left - 1, -1):result.append(matrix[bottom][i])bottom -= 1# 从下到上if left <= right:for i in range(bottom, top - 1, -1):result.append(matrix[i][left])left += 1return resultJava
public class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0) return result;int top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1;while (left <= right && top <= bottom) {// 从左到右for (int i = left; i <= right; i++) {result.add(matrix[top][i]);}top++;// 从上到下for (int i = top; i <= bottom; i++) {result.add(matrix[i][right]);}right--;// 从右到左if (top <= bottom) {for (int i = right; i >= left; i--) {result.add(matrix[bottom][i]);}bottom--;}// 从下到上if (left <= right) {for (int i = bottom; i >= top; i--) {result.add(matrix[i][left]);}left++;}}return result;}public static void main(String[] args) {Solution solution = new Solution();int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};System.out.println(solution.spiralOrder(matrix));}
}相关文章:
力扣热门算法题 52. N 皇后 II,53. 最大子数组和,54. 螺旋矩阵
52. N 皇后 II,53. 最大子数组和,54. 螺旋矩阵,每题做详细思路梳理,配套Python&Java双语代码, 2024.03.20 可通过leetcode所有测试用例。 目录 52. N 皇后 II 解题思路 完整代码 Python Java 53. 最大子数组…...

【OpenVINO】解决OpenVINO在GPU推理中报错的方法
1. 问题描述 使用OpenVINO进行深度学习推理时,通常会借助GPU以提升计算速度。然而,有时候运行程序时候会出现如下错误: <kernel>:8153:2: error: expected identifier or (unroll_for (int i 0; i < TILE_SIZE; i) {^ <kernel…...

AES加密的中文乱码与Java默认编码
0. 背景 win11环境下 java8 idea 开发的项目接口有加密需求,暂时使用AES完成,AES工具类代码如下 public static String aesEncrypt(String content, String key) throws Exception {//指定加密算法Cipher cipher Cipher.getInstance("AES");//创建加密规则&#…...
浏览器和服务器)
Node.js笔记 (二)浏览器和服务器
Ajax Ajax是什么 全称:Asynchronous Javascript And Xml. 用javascript执行异步网络请求,可以说是定义了一种编程行为/习惯。 通信双方:浏览器 和 服务器 特点:异步,所以可以在异步请求服务器,在不刷新页…...

面试经典-32-判断子序列
题目 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列…...

windows使用知识
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言windows使用知识 一、cmd鼠标选中后,程序不运行的解决方案总结 前言 提示:这里可以添加本文要记录的大概内容: windows使用…...

用python如何实现智能合约?如何使用remix编写solidity智能合约并部署上链
目录 用python如何实现智能合约? 直接展示下成功界面 下面分步骤说: remix代码 python链接remix代码...

Electron窗口管理详解:使用BrowserWindow API打造个性化界面
Electron窗口管理详解:使用BrowserWindow API打造个性化界面 创建和初始化窗口窗口定制化窗口操作与事件监听多窗口管理和工作区布局结语 在当今跨平台桌面应用开发领域,Electron 凭借其 JavaScript 与 HTML5 技术栈结合原生操作系统 API 的能力…...
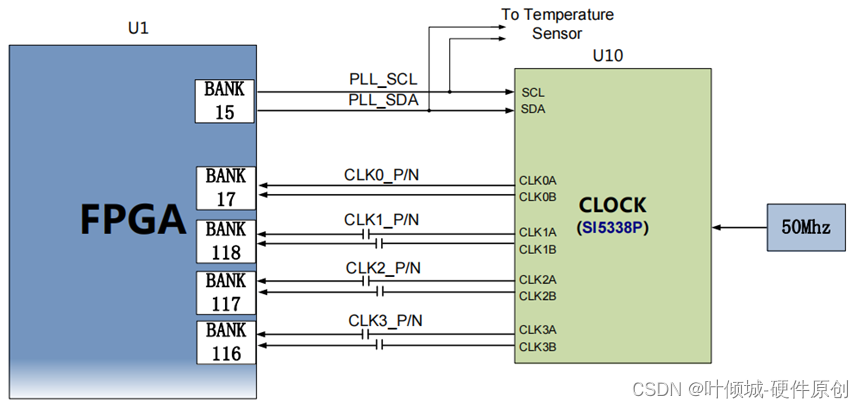
19---时钟电路设计
视频链接 时钟硬件电路设计01_哔哩哔哩_bilibili 时钟电路设计 晶振是数字电路的心脏,数字电路需要一个稳定的工作时钟信号,时钟电路至关重要! 1、晶振概述 晶振一般指晶体振荡器。晶体振荡器是指从一块石英晶体上按一定方位角切下薄片&…...
)
PSNR/SSIM/LPIPS图像质量评估三件套(含代码)
在图像质量评估上,有三个重要指标:PSNR,SSIM,LPIPS。本文提供简易脚本分别实现。 PSNR,峰值信噪比,是基于MSE的像素比较低质量评估,一般30dB以上质量就不错,到40dB以上肉眼就很难分…...
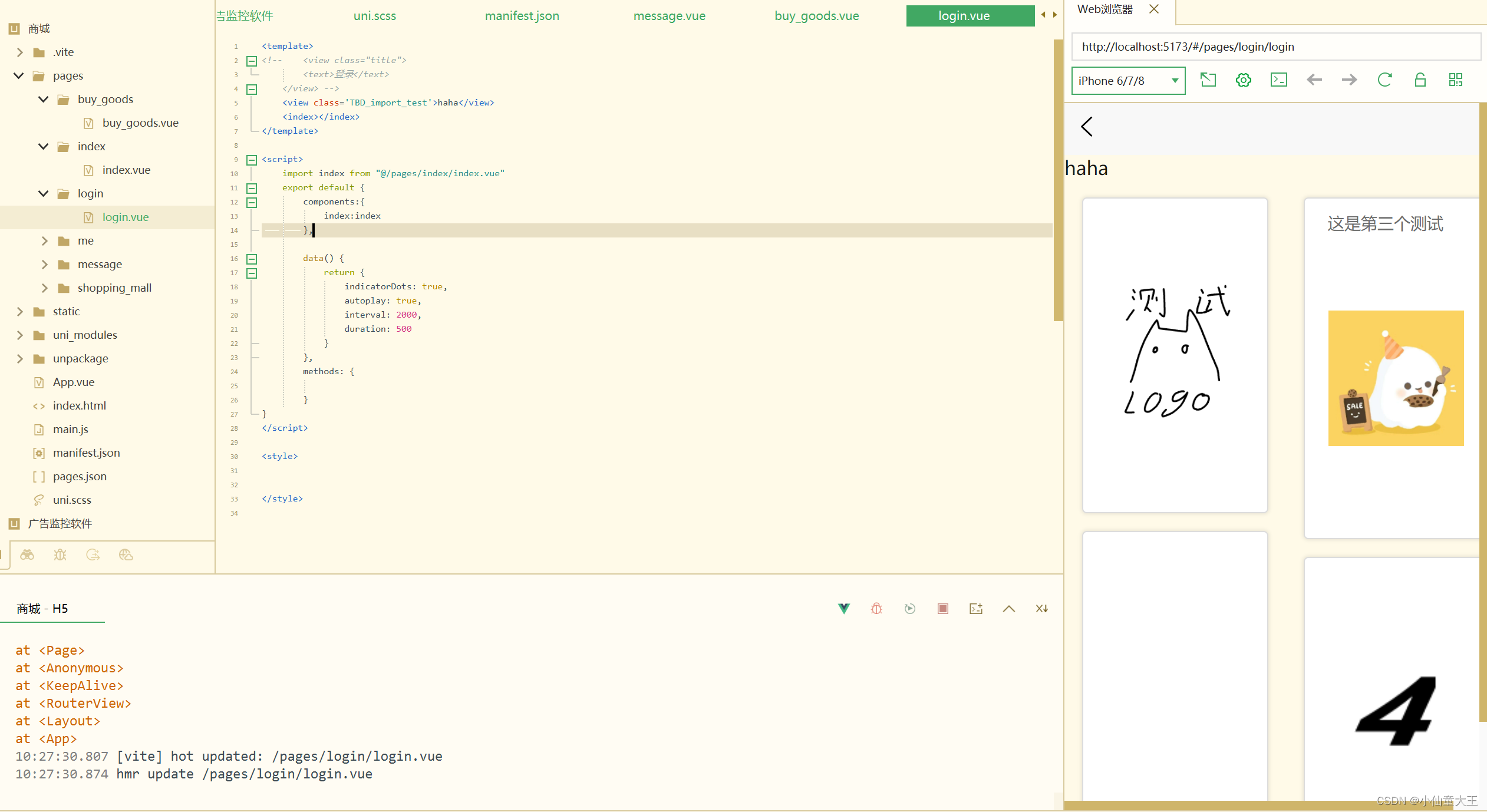
20240318uniapp怎么引用组件
在script中增加 import index from "/pages/index/index.vue" 把index直接整个作为一个组件引入 然后注册组件 在export default中增加 components: {index:index }, 注册了index组件,内容为import的index 然后就可以在template里使用 <index&…...

扩展以太网(数据链路层)
目录 一、在物理层扩展以太网 二、在数据链路层扩展以太网 三、以太网交换机的特点 四、以太网交换机的交换方式 五、以太网交换机的自学习功能 六、小结 一、在物理层扩展以太网 使用光纤扩展: • 主机使用光纤(通常是一对光纤)和…...

每日一练 | 华为认证真题练习Day202
1、在组播网络环境中,如果IGMPv2主机和IGMP V1路由器(以下简称版本2主机和版本1路由器)共同处于同一局域网当中,那他们是如何协同工作的?(多选) A. 版本1路由器把IGMPv2报告看作无效的IGMP信息…...
基于python+vue的幼儿园管理系统flask-django-php-nodejs
随着信息时代的来临,过去的传统管理方式缺点逐渐暴露,对过去的传统管理方式的缺点进行分析,采取计算机方式构建幼儿园管理系统。本文通过课题背景、课题目的及意义相关技术,提出了一种活动信息、课程信息、菜谱信息、通知公告、家…...

【java】java环境变量分类
测试代码: public class TestSys {public static void main(String[] args) {/*** 获取所有的系统环境变量*/Map<String, String> map System.getenv();map.forEach((key, value) -> System.out.printf("env:key:%s->value:%s%n"…...
)
掌握Go语言:Go语言通道,并发编程的利器与应用实例(20)
通道(Channel)是用来在 Go 程序中传递数据的一种数据结构。它是一种类型安全的、并发安全的、阻塞式的数据传输方式,用于在不同的 Go 协程之间传递消息。 基本概念 创建通道:使用make()函数创建一个通道。 ch : make(chan int)…...
-Day9)
JavaSE(上)-Day9
JavaSE(上)-Day9 集合static静态变量静态方法静态方法的注意事项重新认识main方法 继承继承注意事项子类到底能继承父类哪些内容继承中成员变量和成员方法的访问特点重写构造方法的访问特点this & super 集合 因为数组是不可变的,我们在…...

Java 内存模型概述
Java 内存区域 引言: 在并发编程中,需要解决两个问题:线程之间如何通信和线程之间如何同步 通信是指线程之间以何种机制来交换信息 在命令式编程中,通信机制主要分为两种:共享内存和消息传递 Java 的并发采用的是…...

远程桌面安卓版下载 安卓远程控制免费版
远程桌面安卓版下载与安卓远程控制免费版的应用解析 随着移动互联网的快速发展,远程桌面应用逐渐成为了许多用户、特别是技术爱好者和商务人士的必备工具。它们不仅可以在电脑上实现远程控制,还能将这种功能延伸到移动设备上,如安卓手机和平…...
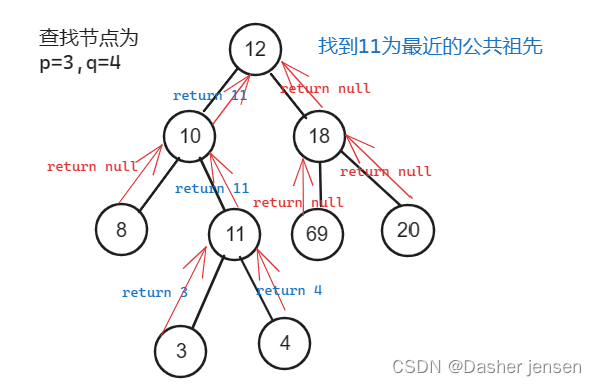
算法打卡day18|二叉树篇07|Leetcode 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先
算法题 Leetcode 530.二叉搜索树的最小绝对差 题目链接:530.二叉搜索树的最小绝对差 大佬视频讲解:二叉搜索树的最小绝对差视频讲解 个人思路 因为是在二叉搜索树求绝对差,而二叉搜索树是有序的,那就把它想成在一个有序数组上求最值&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...