粒子群算法 - 目标函数最优解计算
粒子群算法概念
粒子群算法 (particle swarm optimization,PSO) 由 Kennedy 和 Eberhart 在 1995 年提出,该算法模拟鸟群觅食的方法进行寻找最优解。基本思想:人们发现,鸟群觅食的方向由两个因素决定。第一个是自己当初飞过离食物最近的位置,第二个因素是鸟群中离食物最近的鸟的位置。根据这个两个因素不断的改变自己的位置。最终,整个鸟群都能寻找到食物。

相关知识
1.编码与适应度函数,2.粒子群算法原理,3.粒子群算法流程,4.使用 python 实现粒子群算法。
编码与适应度函数
在粒子群算法中也需要进行编码,不过相对于遗传算法粒子群算法编码非常简单。例如,函数
可直接将函数解作为编码。而函数的值
即可作为适应度,若求解函数最小值则适应度越小越好,若求解函数最大值则适应度越大越好。
粒子群算法原理
粒子群函数是根据鸟群寻找食物实现的优化算法,每一只鸟被称为粒子,即函数的一个解。我们已经知道,每一只鸟寻找食物是根据离食物最近的鸟的位置,与自己曾经离食物最近的位置来决定改变自己现在的位置。根据这个原理,粒子群算法核心公式如下:
其中,为鸟群的位置,
为鸟飞行的速度,即鸟群更新位置的因素。而公式2就是决定速度的因素:
p:个体最佳位置
pg:全局最佳位置
w:惯性权重因子,用来控制速度的更新
c1,c2:加速度常数,通常设为2
r1,r2:0到1之间的随机数粒子群算法流程
随机初始粒子群位置与速度
计算粒子群适应度
根据公式更新粒子群位置与速度
重复2,3直到满足停止条件使用python实现粒子群算法
实现粒子群算法。并求解函数 f(x) 在区间 [-10,10] 上的最小值:
首先我们需要对粒子群位置与速度进行随机初始:
import numpy as np
#初始化粒子群位置
x = np.random.uniform(x_bound[0], x_bound[1],(pop_size, dim))
#初始化粒子群速度
v = np.random.rand(pop_size,dim)其中,x_bound 为 x 取值范围。pop_size 为粒子群大小,即鸟的数量。dim 为搜索空间维度。
再根据 x 计算适应度:
#f(x1,x2)=(x1-4)**2+(x2-5)**2,函数值即适应度
def f(x):return np.sum(np.square(x-np.array([4,5])), axis=1)
#计算适应度
fitness = f(x)同时计算出全局最优位置与个体最优适应度、全局最优适应度:
#全局最优位置
pg = x[np.argmin(fitness)]
#个体最优适应度
individual_best_fitness = fitness
#全局最优适应度
global_best_fitness = np.min(individual_best_fitness)最后开始进化,不断更新粒子群位置:
#encoding=utf8
import numpy as np
pop_size =10#粒子群大小
n_iters = 1000#训练轮数
dim = 2#搜索空间维度
w = 0.6#惯性权重因子
c1 = 2#加速度常数,通常设为2
c2 = 2#加速度常数,通常设为2
x_bound = [-10,10]#函数定义域
def pso(f):'''f:目标函数pg:最优解坐标'''#初始化粒子群位置x = np.random.uniform(low=x_bound[0], high=x_bound[1], size=(pop_size, dim)) #初始化粒子群速度v = np.random.rand(pop_size,dim)#初始个体最佳位置p = x#计算适应度fitness = f(x)#全局最优位置pg = x[np.argmin(fitness)]#个体最优适应度individual_best_fitness = fitness#全局最优适应度global_best_fitness = np.min(individual_best_fitness)#开始进化for i in range(n_iters):#产生随机数r1,r2r1 = np.random.rand(pop_size,dim)r2 = np.random.rand(pop_size,dim)#计算粒子群速度v = w*v+c1*r1*(p-x)+c2*r2*(pg-x)#更新粒子群位置x = v + x#计算更新后的适应度fitness = f(x)#需更新个体update_id = np.greater(individual_best_fitness, fitness)#更新pp[update_id] = x[update_id]#更新个体最优适应度individual_best_fitness[update_id] = fitness[update_id]#更新全局最优位置与全局最优适应度if np.min(fitness) < global_best_fitness:pg = x[np.argmin(fitness)]global_best_fitness = np.min(fitness) return pg相关文章:
粒子群算法 - 目标函数最优解计算
粒子群算法概念 粒子群算法 (particle swarm optimization,PSO) 由 Kennedy 和 Eberhart 在 1995 年提出,该算法模拟鸟群觅食的方法进行寻找最优解。基本思想:人们发现,鸟群觅食的方向由两个因素决定。第一个是自己当初飞过离食物…...

关于MySQL数据库的学习3
目录 前言: 1.DQL(数据查询语言): 1..1基本查询: 1.2条件查询: 1.3排序查询: 1.3.1使用ORDER BY子句对查询结果进行排序。 1.3.2可以按一个或多个列进行排序,并指定排序方向(升序ASC或降序DESC&#…...

笔试题——得物春招实习
开幕式排练 题目描述 导演在组织进行大运会开幕式的排练,其中一个环节是需要参演人员围成一个环形。演出人员站成了一圈,出于美观度的考虑,导演不希望某一个演员身边的其他人比他低太多或者高太多。 现在给出n个参演人员的身高,问…...

动手做简易版俄罗斯方块
导读:让我们了解如何处理形状的旋转、行的消除以及游戏结束条件等控制因素。 目录 准备工作 游戏设计概述 构建游戏窗口 游戏方块设计 游戏板面设计 游戏控制与逻辑 行消除和计分 判断游戏结束 界面美化和增强体验 看看游戏效果 准备工作 在开始编码之前…...

【极简无废话】open3d可视化torch、numpy点云
建议直接看文档,很多都代码老了,注意把代码版本调整到你使用的open3d的版本: https://www.open3d.org/docs/release/tutorial/visualization/visualization.html 请注意open3d应该已经不支持centos了! 从其他格式转换成open3d…...
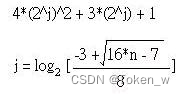
C语言经典算法-6
文章目录 其他经典例题跳转链接31.数字拆解32.得分排行33.选择、插入、气泡排序34.Shell 排序法 - 改良的插入排序35.Shaker 排序法 - 改良的气泡排序 其他经典例题跳转链接 C语言经典算法-1 1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一&…...
【计算机考研】杭电 vs 浙工大 怎么选?
想求稳上岸的话,其他几所学校也可以考虑,以留在本地工作的角度考虑,这几所学校都能满足你的需求。 如果之后想谋求一份好工作,肯定优先杭电是比较稳的,当然复习的时候也得加把劲。 这个也可以酌情考虑,报…...
激活函数
优秀的激活函数: 非线性:激活函数非线性时,多层神经网络可逼近所有函数 可微性:梯度下降更新参数 单调性:当激活函数是单调的,能保证单层网络的损失函数是凸函数 近似恒等性:当参数初始化为…...

使用Jackson进行 JSON 序列化和反序列化
在Spring应用程序中,您可以通过Maven添加Jackson依赖,并创建一个工具类来封装对象的序列化和反序列化方法。以下是详细步骤: 1. 引入 Jackson 依赖 如果使用 Maven,您可以在 pom.xml 文件中添加以下依赖: <depend…...

Linux/Uinx 系统编程:定时器以及时钟同步
本章讨论了定时器和定时器服务;介绍了硬件定时器的原理和基于Intel x86 的PC中的硬件定时器;讲解了CPU操作和中断处理;描述了Linux中与定时器相关的系统调用、库函数和定时器服务命令;探讨了进程间隔定时器、定时器生成的信号,并通过示例演示了进程间隔定时器。编程…...
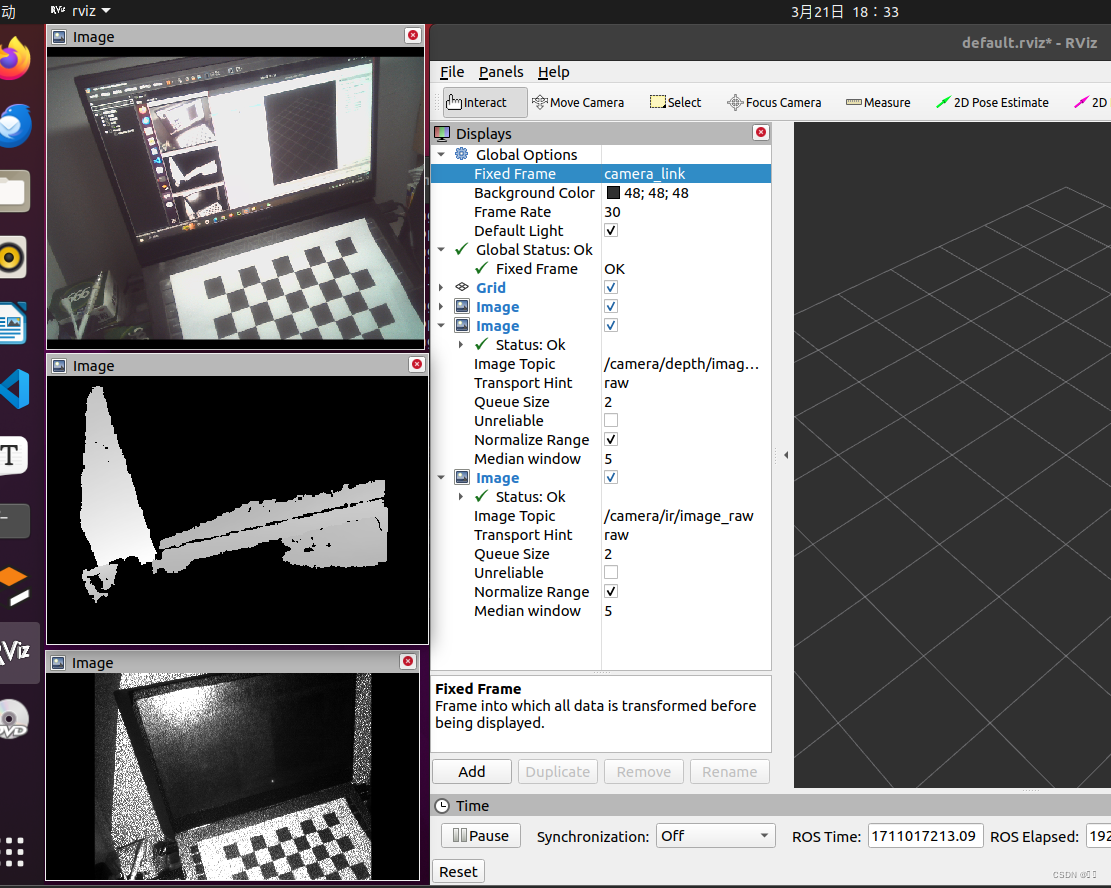
(Ubuntu中调用相机花屏)Astra plus深度相机--rgb彩色图像花屏解决方法之一
在调试深度相机的过程中只能能调出深度图像和红外图像 在rviz的image的topic中选择彩色图像的话题不显示图像 1、查看相机的usb序列号 lsusb如上图所示,此相机的USB序列号是2bc5:050f,2bc5:060f 其中050f是显示彩色图像的 在这里可通过拔插相机来确定序列号是哪几…...

iPaaS平台能帮助企业解决什么问题?
随着数字化转型的推进,越来越多的企业开始关注如何提高业务效率和灵活性。iPaaS作为一种新型集成平台,它能够帮助企业解决许多与应用程序和数据集成相关的问题。 它能给企业解决什么问题? 以下是 iPaaS 平台通常能够帮助企业解决的一些问题…...
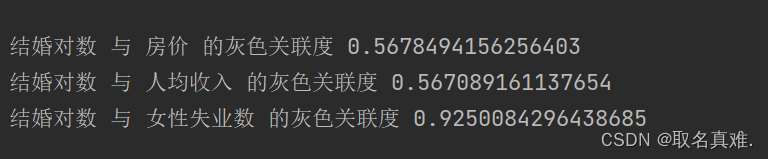
数学建模(灰色关联度 python代码 案例)
目录 介绍: 模板: 案例:哪些原因影响结婚率 数据标准化: 灰色关联度系数: 完整代码: 结果: 介绍: 灰色关联度是一种多指标综合评价方法,用于分析和评价不同指标之…...
【DP】第十四届蓝桥杯省赛C++ B组《接龙数列》(C++)
【题目描述】 对于一个长度为 K 的整数数列:A1,A2,...,AK,我们称之为接龙数列当且仅当 的首位数字恰好等于 的末位数字 (2≤i≤K)。 例如 12,23,35,56,61,11 是接龙数列;12,23,34,56 不是接龙数列,因为 56 的首位数字不等于 3…...
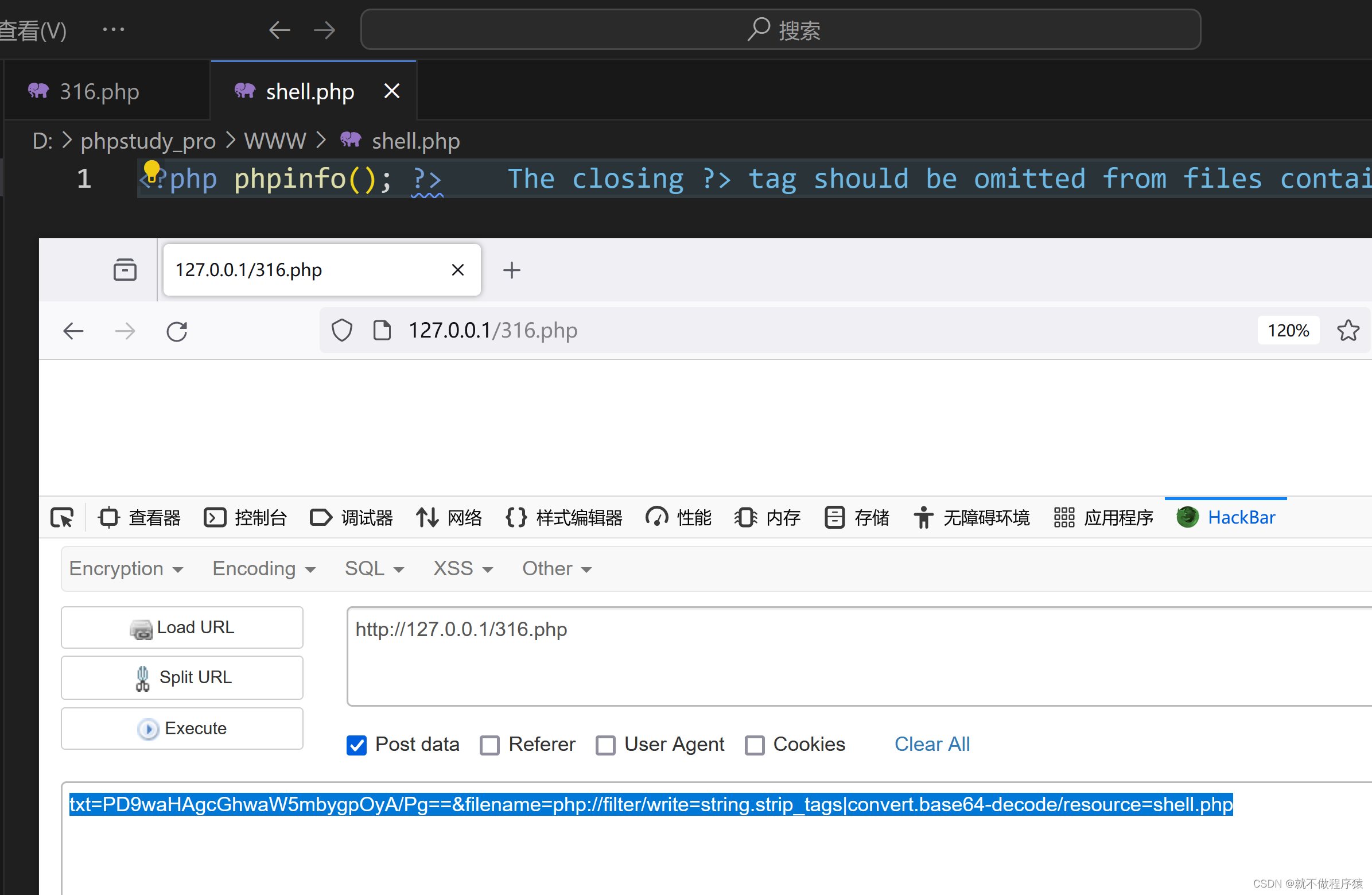
文件包含漏洞(input、filter、zip)
一、PHP://INPUT php://input可以访问请求的原始数据的只读流,将post请求的数据当作php代码执行。当传入的参数作为文件名打开时,可以将参数设为php://input,同时post想设置的文件内容,php执行时会将post内容当作文件内容。从而导致任意代码…...
使用iconv解决Linux/Ubuntu/Debian中gb2312中文文档乱码问题
你可以使用 iconv 命令行工具将文件中的文本从 GB2312 转换为 UTF-8。 你可以这样做: iconv -f GB2312 -t UTF-8 input.txt > output.txt将 input.txt 替换为以 GB2312 编码的输入文件的名称,将 output.txt 替换为你想要的 UTF-8 格式转换文件的名称。…...

图论中的最小生成树:Kruskal与Prim算法深入解析
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:アンビバレント—Uru 0:24━━━━━━️💟──────── 4:02 🔄 ◀️ ⏸ ▶️ ☰ …...
)
uniapp 之 实现商品详情的锚点跳转(类似京东商品详情-点击顶部按钮跳转的对应的页面的内容区域)
类似京东商品详情-点击顶部详情跳转到页面对应的详情区域,点击评价跳转到页面对应的评价区域等。 照例,先封装方法: 封装方法 util.js /*** 锚点跳转(如:商品详情页面跳转)* param {string} targetId 目…...
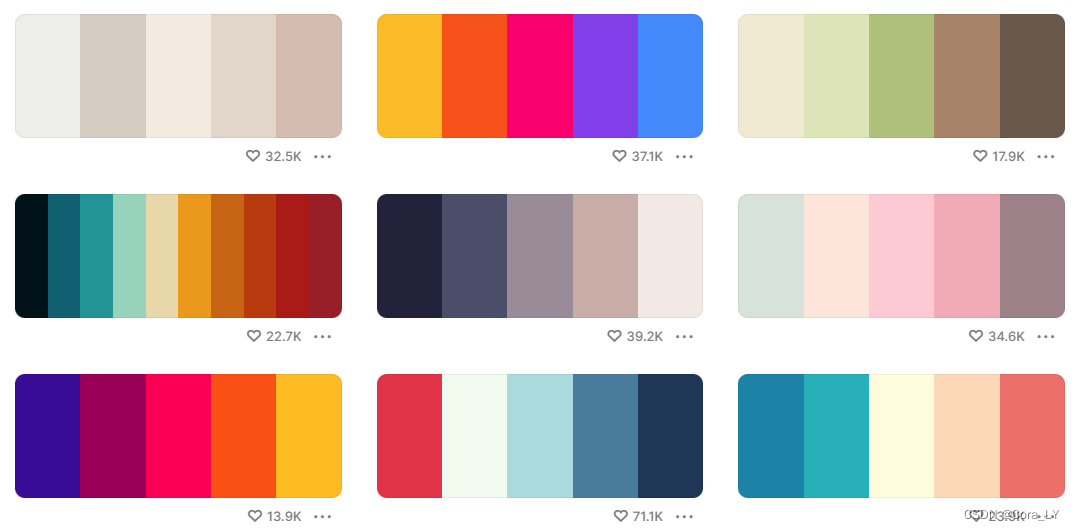
PPT好看配色
放几个链接!画图时候可以参考!转自知乎 Color Hunt ColorDrop 中国色 Flat UI Colors Coolors...
与浏览器环境有何不同)
微信小程序执行环境(微信端)与浏览器环境有何不同
微信小程序执行环境与浏览器环境有很多不同之处,以下是一些例子: 全局对象: 浏览器环境中的 JavaScript 有一个全局对象 window,而微信小程序中的 JavaScript 没有 window 对象,取而代之的是 wx 对象,wx …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
