探索数据结构：双向链表的灵活优势

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 前言

前面我们学习了单链表，它解决了顺序表中插入删除需要挪动大量数据的缺点。但同时也有仍需改进的地方，比如说：我们有时候需要寻找某个节点的前一个节点，对于单链表而言只能遍历，这样就可能造成大量时间的浪费。为了解决这个问题，我们就要学习今天的主角——带头双向循环链表。

2. 双向链表的功能

1. 初始化顺序表中的数据。
2. 对顺序表进行尾插(末尾插入数据)。
3. 对顺序表进行头插(开头插入数据)。
4. 对顺序表进行头删(开头删除数据)。
5. 对顺序表进行尾删(末尾删除数据)。
6. 对顺序表就像查找数据。
7. 对顺序表数据进行修改。
8. 任意位置的删除和插入数据。
9. 打印顺序表中的数据。
10. 销毁顺序表。

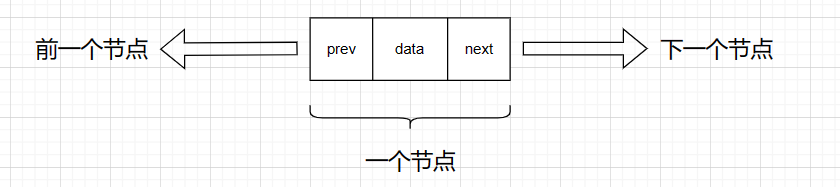
3. 双向链表的定义

双向链表的定义结构体需要包含三个成员，一个成员存储数值，一个成员存储前一个节点的地址，最后一个成员存储下一个节点的地址。

typedef int LTDataType;
typedef struct DoubleList
{struct DoubleList* prev;//指向前一个节点LTDataType data;struct DoubleList* next;//指向下一个节点
}DListNode;

4. 双向链表的功能

4.1 初始化双向链表

在初始化双向链表时，我们需要创建一个头节点，也就是我们常说的哨兵位头节点。

(1) 创建头结点

DListNode* DLNodeCreat(LTDataType x)
{DListNode* newnode = (DListNode*)malloc(sizeof(DListNode));if (newnode == NULL){perror("malloc fail:");return NULL;}newnode->prev = NULL;newnode->next = NULL;newnode->data = x;return newnode;
}

(2) 初始化

初始化将头节点的前后指针都指向自己，并将数值至为-1。

DListNode* InitDList()
{DListNode* phead = DLNodeCreat(-1);phead->prev = phead;phead->next = phead;return phead;
}

(3) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.2 双向链表尾插

因为我们实现的双向链表存在头节点，所以我们不需要像实现单链表一样先判断链表是否为空。

(1) 代码实现

void DListPushBack(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* tail = ptr->prev;DListNode* newnode = DLNodeCreat(x);tail->next = newnode;newnode->prev = tail;ptr->prev = newnode;newnode->next = ptr;
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.3 双向链表头插

因为带头双向循环链表的特性，即使只有头节点进行头插，代码实现也是相同的。

(1) 代码实现

void DListPushFront(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* next = ptr->next;DListNode* newnode = DLNodeCreat(x);ptr->next = newnode;newnode->prev =ptr;newnode->next = next;next->prev = newnode;
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.4 双向链表尾删

有了循环找尾节点也十分容易，双向链表尾删自然并不困难。但是需要防止删除头节点。

(1) 代码实现

void DListPopBack(DListNode* ptr)
{assert(ptr);assert(ptr->next != ptr);//放置删除头节点DListNode* tail = ptr->prev;DListNode* tailprev = tail->prev;free(tail);tail == NULL;tailprev->next = ptr;ptr->prev = tailprev;
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.5 双向链表头删

头删与尾删一样，都需要防止删除头节点。

(1) 代码实现

void DListPopFront(DListNode* ptr)
{assert(ptr);assert(ptr->next != ptr);DListNode* phead = ptr->next;DListNode* pheadnext = phead->next;free(phead);ptr->next = pheadnext;pheadnext->prev = ptr;
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.6 双向链表查找

和单链表一样，我们也可以对双向链表进行查找。如果找到就返回该节点的地址，否则返回NULL。

(1) 代码实现

DListNode* DListFind(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* cur = ptr->next;while (cur != ptr){if (cur->data == x){return cur;}cur = cur->next;}return NULL;
}

(2) 复杂度分析

• 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.7 修改双向链表

我们可以结合双向链表的查找，对双向链表进行修改。

(1) 代码实现

void DListModify(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);assert(ptr != pos);//防止对头节点操作DListNode* cur = ptr->next;while (cur != ptr){if (cur == pos){cur->data = x;}cur = cur->next;}
}

(2) 复杂度分析

• 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.8 双向链表指定插入数据

随机插入数据可以分为：向前插入与向后插入。

(1) 向前插入

void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);DListNode* newnode = DLNodeCreat(x);DListNode* prev = pos->prev;newnode->prev = prev;newnode->next = pos;prev->next = newnode;pos->prev = newnode;
}

(2) 向后插入

void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);DListNode* newnode = DLNodeCreat(x);DListNode* next = pos->next;newnode->prev = pos;newnode->next = next;next->prev = newnode;pos->next = newnode;
}

(3) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.9 指定位置删除数据

任意删除也需要放置删除头节点，并且因为其特点只需要一个参数就能完成该操作。

(1) 代码实现

void DListErase(DListNode* pos)
{assert(pos);assert(pos != pos->next);pos->prev->next = pos -> next;pos->next->prev = pos->prev;free(pos);pos = NULL;
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.10 打印双向链表

打印双向链表只需将循环之前的数据全部打印即可。

(1) 代码实现

void DLTPrint(DListNode* ptr)
{assert(ptr);printf("guard");DListNode* cur = ptr->next;while (cur != ptr){printf("<==>%d", cur->data);cur = cur->next;}printf("\n");
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.11 销毁双向链表

(1) 代码实现

void DListDestroy(DListNode* ptr)
{assert(ptr);DListNode* cur = ptr->next;while (cur != ptr){DListNode* next = cur->next;free(cur);cur = next;}free(ptr);
}

(2) 复杂度分析

• 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
• 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5. 完整代码

5.1 DList.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int LTDataType;
typedef struct DoubleList
{struct DoubleList* prev;//指向前一个节点LTDataType data;struct DoubleList* next;//指向下一个节点
}DListNode;
DListNode* InitDList();//初始化
void DListPushBack(DListNode* ptr, LTDataType x);//尾插
void DLTPrint(DListNode* ptr);//打印
void DListPushFront(DListNode* ptr, LTDataType x);//头插
void DListPopBack(DListNode* ptr);//尾删
void DListPopFront(DListNode* ptr);//头删
DListNode*DListFind(DListNode* ptr, LTDataType x);//查找
void DListModify(DListNode* ptr, DListNode* pos);//修改
void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x);//任意位置之前插入
void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x);//任意位置之后插入
void DListErase(DListNode* pos);//任意位置删除
void DListDestroy(DListNode* ptr);//销毁双向链表

5.2 DList.c

#include"DoubleList.h"
DListNode* DLNodeCreat(LTDataType x)
{DListNode* newnode = (DListNode*)malloc(sizeof(DListNode));if (newnode == NULL){perror("malloc fail:");return NULL;}newnode->prev = NULL;newnode->next = NULL;newnode->data = x;return newnode;
}
DListNode* InitDList()
{DListNode* phead = DLNodeCreat(-1);phead->prev = phead;phead->next = phead;return phead;
}
void DListPushBack(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* tail = ptr->prev;DListNode* newnode = DLNodeCreat(x);tail->next = newnode;newnode->prev = tail;ptr->prev = newnode;newnode->next = ptr;
}
void DListPushFront(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* next = ptr->next;DListNode* newnode = DLNodeCreat(x);ptr->next = newnode;newnode->prev =ptr;newnode->next = next;next->prev = newnode;
}
void DListPopBack(DListNode* ptr)
{assert(ptr);assert(ptr->next != ptr);//放置删除头节点DListNode* tail = ptr->prev;DListNode* tailprev = tail->prev;free(tail);tail == NULL;tailprev->next = ptr;ptr->prev = tailprev;
}
void DListPopFront(DListNode* ptr)
{assert(ptr);assert(ptr->next != ptr);DListNode* phead = ptr->next;DListNode* pheadnext = phead->next;free(phead);ptr->next = pheadnext;pheadnext->prev = ptr;
}
DListNode* DListFind(DListNode* ptr, LTDataType x)
{assert(ptr);DListNode* cur = ptr->next;while (cur != ptr){if (cur->data == x){return cur;}cur = cur->next;}return NULL;
}
void DListModify(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);assert(ptr != pos);//防止对头节点操作DListNode* cur = ptr->next;while (cur != ptr){if (cur == pos){cur->data = x;}cur = cur->next;}
}
void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);DListNode* newnode = DLNodeCreat(x);DListNode* prev = pos->prev;newnode->prev = prev;newnode->next = pos;prev->next = newnode;pos->prev = newnode;
}
void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x)
{assert(ptr);DListNode* newnode = DLNodeCreat(x);DListNode* next = pos->next;newnode->prev = pos;newnode->next = next;next->prev = newnode;pos->next = newnode;
}
void DListErase(DListNode* pos)
{assert(pos);assert(pos != pos->next);pos->prev->next = pos -> next;pos->next->prev = pos->prev;free(pos);pos = NULL;
}
void DLTPrint(DListNode* ptr)
{assert(ptr);printf("guard");DListNode* cur = ptr->next;while (cur != ptr){printf("<==>%d", cur->data);cur = cur->next;}printf("\n");
}
void DListDestroy(DListNode* ptr)
{assert(ptr);DListNode* cur = ptr->next;while (cur != ptr){DListNode* next = cur->next;free(cur);cur = next;}free(ptr);
}