机器学习----交叉熵(Cross Entropy)如何做损失函数
目录
一.概念引入
1.损失函数
2.均值平方差损失函数
3.交叉熵损失函数
3.1信息量
3.2信息熵
3.3相对熵
二.交叉熵损失函数的原理及推导过程
表达式
二分类
联立
取对数
补充
三.交叉熵函数的代码实现
一.概念引入
1.损失函数
损失函数是指一种将一个事件(在一个样本空间中的一个元素)映射到一个表达与其事件相关的经济成本或机会成本的实数上的一种函数。在机器学习中,损失函数通常作为学习准则与优化问题相联系,即通过最小化损失函数求解和评估模型。
不同的任务类型需要不同的损失函数,例如在回归问题中常用均方误差作为损失函数,分类问题中常用交叉熵作为损失函数。
2.均值平方差损失函数
定义如下:
意义:N为样本数量。公式表示为每一个真实值与预测值相减的平方去平均值。均值平方差的值越小,表明模型越好。
对于回归问题,均方差的损失函数的导数是局部单调的,可以找到最优解。但是对于分类问题,损失函数可能是坑坑洼洼的,很难找到最优解。故均方差损失函数适用于回归问题。
3.交叉熵损失函数
交叉熵是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性。在机器学习中,交叉熵表示真实概率分布与预测概率分布之间的差异。其值越小,模型预测效果就越好。
交叉熵损失函数的公式为:
其中,y表示样本的真实标签,\hat{y}表示模型预测的标签。当y=1时,表示样本属于正类;当y=0时,表示样本属于负类。
3.1信息量
信息量是指信息多少的量度。
比如说
- 1:太阳从东边升起,这个信息量就是0,因为这个是一句废话。没有不确定性的东西。
- 2:今天会下雨。从直觉上来看,这个信息量就比较大了,因为今天天气具有不确定性,但是这句话消除了不确定性。
根据上述总结如下:信息量的大小与信息发生的概率成反比。概率越大,信息量就越小,概率越小,信息量就越大。设某件事发生的概率为p(xi),则信息量为:
3.2信息熵
信息熵是信息论中的一个重要概念,用于衡量一个系统或信号中信息量的不确定性或随机性。
信息熵的定义可以用数学公式表示。假设有一个离散的随机变量X,它可以取n个不同的可能值,每个可能值的概率为
,则信息熵H(X)的计算公式为:
其中,表示以2为底的对数。
信息熵的物理意义是:它表示了在给定概率分布的情况下,系统的平均不确定性或信息量。信息熵的值越大,表示系统的不确定性越高;信息熵的值越小,表示系统的不确定性越低。
3.3相对熵
相对熵,也称为KL 散度(Kullback-Leibler Divergence),是一种用于比较两个概率分布差异的度量。它衡量了一个概率分布P与另一个参考概率分布Q之间的差异程度。
相对熵的定义为:
其中,P(x)和Q(x)分别是概率分布P和Q在事件x上的概率。
相对熵的物理意义是:它表示了将概率分布P表示为参考概率分布Q的编码时所需的额外信息量。如果P和Q非常接近,相对熵的值会比较小;如果P和Q差异较大,相对熵的值会比较大。
KL散度=交叉熵-信息熵
相对熵在机器学习、信息论和统计学中有广泛的应用。它可以用于评估两个模型或概率分布的相似性,比较数据分布的差异,以及在熵最小化的框架下进行优化等。
例如,在机器学习中,相对熵常用于比较真实数据的分布和模型预测的分布之间的差异,以评估模型的性能。较小的相对熵值表示模型预测的分布与真实分布更接近。
二.分类问题中的交叉熵
1.二分类问题中的交叉熵
把二分类的交叉熵公式 4 分解开两种情况:
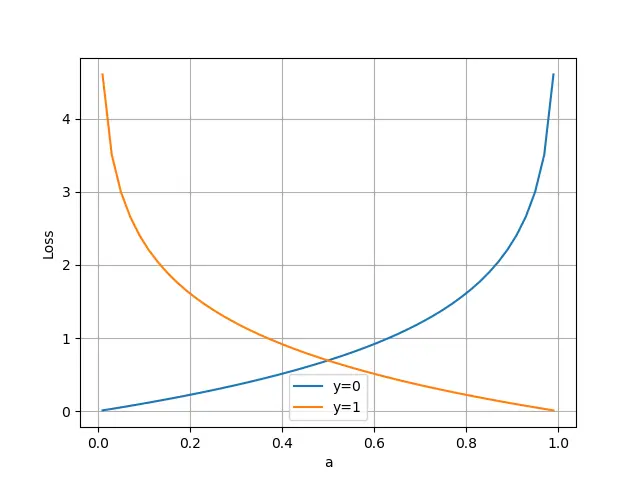
- 当 y=1 时,即标签值是 1 ,是个正例,加号后面的项为:
- 当 y=0 时,即标签值是 0 ,是个反例,加号前面的项为 0 :
横坐标是预测输出,纵坐标是损失函数值。 y=1 意味着当前样本标签值是1,当预测输出越接近1时,损失函数值越小,训练结果越准确。当预测输出越接近0时,损失函数值越大,训练结果越糟糕。此时,损失函数值如下图所示。
2.多分类问题中的交叉熵
假设希望根据图片动物的轮廓、颜色等特征,来预测动物的类别,有三种可预测类别:猫、狗、猪。假设我们训练了两个分类模型,其预测结果如下:
模型1:
预测值 标签值 是否正确 0.3 0.3 0.4 0 0 1(猪) 正确 0.3 0.4 0.4 0 1 0(狗) 正确 0.1 0.2 0.7 1 0 0(猫) 错误 每行表示不同样本的预测情况,公共 3 个样本。可以看出,模型 1 对于样本 1 和样本 2 以非常微弱的优势判断正确,对于样本 3 的判断则彻底错误。
模型2:
预测值 标签值 是否正确 0.1 0.2 0.7 0 0 1(猪) 正确 0.1 0.7 0.2 0 1 0(狗) 正确 0.3 0.4 0.4 1 0 0(猫) 错误 可以看出,模型 2 对于样本 1 和样本 2 判断非常准确(预测概率值更趋近于 1),对于样本 3 虽然判断错误,但是相对来说没有错得太离谱(预测概率值远小于 1)。
结合多分类的交叉熵损失函数公式可得,模型 1 的交叉熵为:
sample 1 loss = -(0 * log(0.3) + 0 * log(0.3) + 1 * log(0.4)) = 0.91
sample 1 loss = -(0 * log(0.3) + 1 * log(0.4) + 0 * log(0.4)) = 0.91
sample 1 loss = -(1 * log(0.1) + 0 * log(0.2) + 0 * log(0.7)) = 2.30
对所有样本的
loss求平均:
模型 2 的交叉熵为:
sample 1 loss = -(0 * log(0.1) + 0 * log(0.2) + 1 * log(0.7)) = 0.35
sample 1 loss = -(0 * log(0.1) + 1 * log(0.7) + 0 * log(0.2)) = 0.35
sample 1 loss = -(1 * log(0.3) + 0 * log(0.4) + 0 * log(0.4)) = 1.20
对所有样本的
loss求平均:
可以看到,0.63 比 1.37 的损失值小很多,这说明预测值越接近真实标签值,即交叉熵损失函数可以较好的捕捉到模型 1 和模型 2 预测效果的差异。交叉熵损失函数值越小,反向传播的力度越小。
参考文章-损失函数|交叉熵损失函数。
三.交叉熵损失函数的原理及推导过程
表达式
输出标签表示为10,1}时,损失函数表达式为:
二分类
二分类问题,假设
正例:公式1
反例:
公式2
联立
将上述两式连乘。
; 其中
公式3
当y=1时,公式3和公式1一样。
当y=0时,公式3和公式2一样。取对数
取对数,方便运算,也不会改变函数的单调性。
公式4
我们希望越大越好,即让负值
越小越好,
得到损失函数为
公式5
补充
上面说的都是一个样本的时候,多个样本的表达式是:多个样本的概率即联合概率,等于每个的乘积。
由公式4和公式5得到
加上对式子进行缩放。便于计算。
或者写作
四.交叉熵函数的代码实现
在Python中,可以使用NumPy库或深度学习框架(如TensorFlow、PyTorch)来计算交叉熵损失函数。以下是使用NumPy计算二分类和多分类交叉熵损失函数的示例代码:
import numpy as np# 二分类交叉熵损失函数 def binary_cross_entropy_loss(y_true, y_pred):return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))# 多分类交叉熵损失函数 def categorical_cross_entropy_loss(y_true, y_pred):num_classes = y_true.shape[1]return -np.mean(np.sum(y_true * np.log(y_pred + 1e-9), axis=1))# 示例用法 # 二分类 y_true_binary = np.array([[0], [1], [1], [0]]) y_pred_binary = np.array([[0.1], [0.9], [0.8], [0.4]]) loss_binary = binary_cross_entropy_loss(y_true_binary, y_pred_binary) print("Binary Cross-Entropy Loss:", loss_binary)# 多分类 y_true_categorical = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) y_pred_categorical = np.array([[0.7, 0.2, 0.1], [0.1, 0.8, 0.1], [0.2, 0.2, 0.6]]) loss_categorical = categorical_cross_entropy_loss(y_true_categorical, y_pred_categorical) print("Categorical Cross-Entropy Loss:", loss_categorical)请注意,上述代码示例仅用于演示目的,实际使用中可能会使用深度学习框架提供的交叉熵损失函数,因为它们通常更加优化和稳定。例如,在TensorFlow中,可以使用tf.keras.losses.BinaryCrossentropy和tf.keras.losses.CategoricalCrossentropy类来计算二分类和多分类交叉熵损失函数。在PyTorch中,可以使用torch.nn.BCELoss和torch.nn.CrossEntropyLoss类来计算相应的损失函数。
代码来自于https://blog.csdn.net/qlkaicx/article/details/136100406
五.交叉熵函数优缺点
1.优点
在用梯度下降法做参数更新的时候,模型学习的速度取决于两个值:
1、学习率;
2、偏导值;
其中,学习率是我们需要设置的超参数,所以我们重点关注偏导值。从上面的式子中,我们发现,偏导值的大小取决于
和
,我们重点关注后者,后者的大小值反映了我们模型的错误程度,该值越大,说明模型效果越差,但是该值越大同时也会使得偏导值越大,从而模型学习速度更快。所以,使用逻辑函数得到概率,并结合交叉熵当损失函数时,在模型效果差的时候学习速度比较快,在模型效果好的时候学习速度变慢。
2.缺点
Deng在2019年提出了ArcFace Loss,并在论文里说了Softmax Loss的两个缺点:
- 1、随着分类数目的增大,分类层的线性变化矩阵参数也随着增大;
- 2、对于封闭集分类问题,学习到的特征是可分离的,但对于开放集人脸识别问题,所学特征却没有足够的区分性。对于人脸识别问题,首先人脸数目(对应分类数目)是很多的,而且会不断有新的人脸进来,不是一个封闭集分类问题。
另外,sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息,因为它采用了类间竞争机制,它只关心对于正确标签预测概率的准确性,忽略了其他非正确标签的差异,导致学习到的特征比较散。基于这个问题的优化有很多,比如对softmax进行改进,如L-Softmax、SM-Softmax、AM-Softmax等。
相关文章:
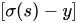
机器学习----交叉熵(Cross Entropy)如何做损失函数
目录 一.概念引入 1.损失函数 2.均值平方差损失函数 3.交叉熵损失函数 3.1信息量 3.2信息熵 3.3相对熵 二.交叉熵损失函数的原理及推导过程 表达式 二分类 联立 取对数 补充 三.交叉熵函数的代码实现 一.概念引入 1.损失函数 损失函数是指一种将一个事件&#x…...

Linux docker3--数据卷-nginx配置示例
一、因为docker部署服务都是以最小的代价部署,所以通常在容器内部很多依赖和命令无法执行。进入容器修改配置的操作也比较麻烦。本例介绍的数据卷作用就是将容器内的配置和宿主机文件打通,之后修改宿主机的配置文件就相当于修改了docker进程的配置文件&a…...

力扣454. 四数相加 II
思路:把四个数组拆成两对,两个分别相加,记录第一对的相加结果进map里,再把第二对数组 0-nums2-nums4 去map里面找出现了几次,这题不用对重复的四元组去重,所以出现多次都有效。 class Solution {public int…...
vulnstack1 渗透分析 红日靶场(一)
环境搭建 ip段设置 kali (coleak):192.168.145.139 Windows 7 (stu1):192.168.10.181、192.168.145.140 Winserver 2008 (owa):192.168.10.180 Win2k3 (root-tvi862ubeh):192.168.10.182复制 kali可以访问win7,但不能…...
外包干了6天,技术明显进步。。。
我是一名大专生,自19年通过校招进入湖南某软件公司以来,便扎根于功能测试岗位,一晃便是近四年的光阴。今年8月,我如梦初醒,意识到长时间待在舒适的环境中,已让我变得不思进取,技术停滞不前。更令…...

比较好的知识点
2023年Java超全面试题及答案解析---https://blog.csdn.net/qq_42301302/article/details/128785274 7分钟带你细致解析4个Java算法必刷题---https://blog.csdn.net/hcxy2022/article/details/127963797 50道JAVA基础算法编程题【内含分析、程序答案】---https://blog.csdn.net/…...
抖音开放平台的订单类API接口调用测试指南(内含详细步骤)
一、什么是抖音开放平台 抖音开放平台基于抖音母体,提供抖音服务基础设施和创新行业解决方案的平台。同时满足各类各类机构、创作者及服务商对于内容获取、分享的个性化需求,我们诚邀各个行业、不同阶段的合作伙伴与我们一起,共建内容良性生…...

HiveSQL一本通 - 案例实操
文章目录 0.HiveSQL一本通使用说明6.综合案例练习之基础查询6.1 环境准备创建数据表数据准备加载数据 6.2 简单查询练习1.查询姓名中带“山”的学生名单2.查询姓“王”老师的个数3.检索课程编号为“04”且分数小于60的学生的分数信息,结果按分数降序排列4.查询数学成…...
Axure RP 8中文---快速原型设计工具,一站式解决方案
Axure RP 8是一款专业的快速原型设计工具,以其直观易用的界面和丰富的功能受到广大用户的青睐。它支持用户通过拖放操作快速创建交互式原型,包括线框图、流程图等,并具备高保真度的设计能力。Axure RP 8还提供了团队协作和共享功能࿰…...

Available platform plugins are: minimal, offscreen, webgl, windows.
我在运行pyqt5开发的代码时,报错: This application failed to start because no Qt platform plugin could be initialized, Reinstalling the application may fix this problem. Available platform plugins are: minimal, offscreen, webgl, windows…...

创意无限,风险有度:2024愚人节海外网红营销策略解析
2024年愚人节即将到来,这个充满趣味与惊喜的节日,既是人们展示幽默与创意的舞台,也是品牌进行营销活动的绝佳时机。在这个特殊的日子里,通过海外网红营销来推广品牌或产品,无疑是一种富有创意的营销策略,但…...

深入理解 Session、Cookie 和 Token:网络安全和身份验证的重要概念
深入理解 Session、Cookie 和 Token:网络安全和身份验证的重要概念 在当今数字化的世界中,网络安全和身份验证是至关重要的议题。为了实现这些目标,我们常常使用诸如 Session、Cookie 和 Token 等概念。这些概念在 Web 开发、网络通信和安全…...

镜像站汇总
软件镜像站 查看linux版本,常见有centos, ubuntu, Debian cat /etc/os-release去清华软件源帮助页面,查找对应源设置方案(需要结合具体的系统版本),常用: Debian https://mirrors.tuna.tsinghua.edu.cn/help/debian/ 需要选则系…...

设计模式之抽象工厂模式解析
抽象工厂模式 1)问题 工厂方法模式中的每个工厂只生产一类产品,会导致系统中存在大量的工厂类,增加系统的开销。 2)概述 a)产品族 和 产品等级结构 产品等级结构:产品的继承结构; 产品族&…...

【毕设级项目】基于ESP8266的家庭灯光与火情智能监测系统——文末源码及PPT
目录 系统介绍 硬件配置 硬件连接图 系统分析与总体设计 系统硬件设计 ESP8266 WIFI开发板 人体红外传感器模块 光敏电阻传感器模块 火焰传感器模块 可燃气体传感器模块 温湿度传感器模块 OLED显示屏模块 系统软件设计 温湿度检测模块 报警模块 OLED显示模块 …...
UnityShader(十九) AlphaBlend
上代码: Shader "Shader入门/透明度效果/AlphaBlendShader" {Properties{_MainTex ("Texture", 2D) "white" {}_AlphaScale("AlphaScale",Range(0,1))1.0}SubShader{Tags { "RenderType""Transparent&quo…...

3D Tiles语义分割流水线
Dylan Chua 和 Anne Lee 开发了一个处理管线,用于对 3D Tiles 中包含的 GL 传输格式 (glTF) 模型进行语义分割。 该管道读取并遍历 3D Tileset,以输出包含元数据的经过转换的划分对象集。 该项目为 3D 语义分割器提供了最小可行产品,作为各种…...
txt、pdf等文件转为一行一行的doccano数据集输入格式
文章目录 doccano 数据集导入简介代码实现代码运行结果代码公开 doccano 数据集导入 在Doccano 导入数据集时,使用TextLine的文件格式,导入的文件需要为一行一行文本的数据格式,每一行文本在导入Doccano后就是一条数据。 简介 主要工作说明…...
java Flink(四十二)Flink的序列化以及TypeInformation介绍(源码分析)
Flink的TypeInformation以及序列化 TypeInformation主要作用是为了在 Flink系统内有效地对数据结构类型进行管理,能够在分布式计算过程中对数据的类型进行管理和推断。同时基于对数据的类型信息管理,Flink内部对数据存储也进行了相应的性能优化。 Flin…...

社科赛斯考研:二十二载岁月铸辉煌,穿越周期的生命力之源
在考研培训行业的浩瀚海洋中,社科赛斯考研犹如一艘稳健的巨轮,历经二十二载风礼,依然破浪前行。在考研市场竞争白热化与学生对于考研机构要求越来越高的双重影响下,社科赛斯考研却以一种分蘖成长的姿态,扎根、壮大&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...