【Redis】缓存穿透
问题发生背景:客户端请求的数据再缓存中和数据库中都不存在。
导致的问题:缓存永远不会生效,这些请求都会去请求数据库—导致数据库压力增大。
解决方案:
1.缓存空对象
在Redis中缓存空对象,告诉客户端数据库中没有该值。 该方法得设置一个短时间的TTL。
优点:实现简单,维护方便
缺点:会有额外的内存消耗,可能造成短期的不一致。 —数据库更新的时候,缓存还没变。
2.布隆过滤:

总体思路如上图所示,就是在客户端取数据的时候先访问布隆过滤器,得到数据库是否包含该数据的结果,有再访问没有就不访问。
布隆过滤器原理:
其实这就是一个哈希算法,哈希查询算法,
哈希算法是借助哈希表查找目标元素的方法,其中用的是哈希函数。
key = f(value)。f()是哈希函数,得到的结果是目标元素的key。
而在布隆过滤器这里,我们不需要知道目标元素的key,我们只需要知道这个元素存不存在,所以,我们的散列函数里面存储的就是0和1,0表示不存在,1表示存在。
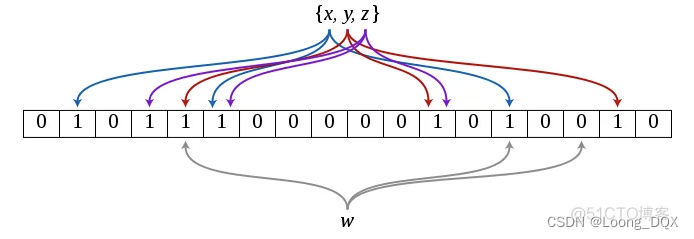
而布隆过滤器的实现:
- 建立一个二进制向量,将所有位设置为0.
- 选定k个散列函数,用于对元素进行k次散列,计算向量的位下标。
- 添加元素,每添加一个就用k个散列函数分别作用于元素,生成对应下标,并将对应的值设为1.
- 检查元素,检查一遍是否都是1。
相关文章:

【Redis】缓存穿透
问题发生背景:客户端请求的数据再缓存中和数据库中都不存在。 导致的问题:缓存永远不会生效,这些请求都会去请求数据库—导致数据库压力增大。 解决方案: 1.缓存空对象 在Redis中缓存空对象,告诉客户端数据库中没有该值…...

编程出现bug?怎么用Python打印异常
在 Python 编程中,异常是指程序执行过程中出现的错误或异常情况。当程序遇到异常时,为了更好地调试和定位问题,我们需要打印异常信息。本文将详细介绍如何在 Python 中打印异常,并提供一些示例和注意事项。 一、try-except 语句捕…...

P1958 上学路线
题目传送门:P1958 上学路线 一个DFS求迷宫的的题。 详细在代码里: #include <bits/stdc.h>using namespace std; int n,m,a[20][20],t,x,y,ans0; int dx[4]{0,1}; int dy[4]{1,0}; int flag[105][105]{0}; inline void dfs(register int x,regis…...

Android14之HIDL报错:Invalid sparse file format at header magic(一百九十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
旭日x3派目标跟随小车
目标跟随小车(yolov5、安全帽识别) 前言最终结果接线实现 前言 上板运行的后处理使用cython封装了,由于每个版本的yolo输出的形状不一样,这里只能用yolov5-6.2这个版本。 ①训练自己的模型并部署于旭日x3派参考: http…...

金潮实业邀您参观2024长三角快递物流展览会
展会介绍 本届展会致力于全面展示快递物流上下游领域的创新解决方案,涵盖快递物流供应链、智能装备、AGV机器人与无人搬运、自动识别、智慧仓储、智慧物流、无人配送、新能物流车及商用车、绿色包装、冷链物流等各个环节,为促进行业合作共融,…...

【超细完整版】C# WebService 通过URL生成WSDL文件和DLL文件 【生成篇】
先学生成,再看调用哦 【超细完整版】C# 获取WebService所有方法并调用 【调用篇】 目的 支持通过web url (自适应“?wsdl”的有无) 生成.wsdl文件 和 .dll文件 实现 将通过一个类的三部分来实现这些功能 获取url中的ClassName (GetClassNameFromUrl&a…...

申请公派访问学者难不难?
申请公派访问学者,对许多人来说是一项具有挑战性的任务。这需要充分的准备和计划,以确保申请能够顺利进行并最终获得批准。下面将探讨一些关于申请公派访问学者的问题以及应对策略。 首先,申请公派访问学者需要有一个明确的研究计划或合作意向…...

关于汽车中网改装需要报备吗?(第二天)
车联网改造需要申报吗? 今天2022年10月20日,小编就给大家介绍一下车联网改装是否需要申报的相关知识。 让我们来看看。 汽车格栅改装无需申报。 这种年检可以直接通过。 您不必担心,因为汽车格栅对于实车的外观来说并不陌生,因此…...

面试官:对于 Java 中多态的理解是什么?
面试官:对于 Java 中多态的理解是什么? 题目 面试官:对于 Java 中多态的理解是什么? 推荐解析 1.父类的引用指向子类的对象 子类重写父类的方法:子类可以继承父类的方法,并对其进行重写。当通过父类的…...

JUC-1M/75±5°超小型密封温度继电器 体积小、重量轻、控温精度高 JOSEF约瑟
JUC系列温度继电器 JUC-1M型超小型密封温度继电器 JUC-2M型超小型密封温度继电器 继电器JUC-027M/2531H-III-G温度继电器 JUC-1M 10C常开温度继电器 JUC-1M 105C温度继电器 用途 小型温控开关系接触感应式密封温度继电器,具有体积小、重量轻、控温精度高等特点&…...

filebeat 配置
主要就是证书的配置 ca_trusted_fingerprint: 产生方式 openssl x509 -fingerprint -sha256 -in /etc/elasticsearch/certs/http_ca.crt 产生的结果 SHA256 Fingerprint 中的冒号 替换掉就是我们想要的结果 ssl: enabled: true ca_trusted_fingerprint: "…...
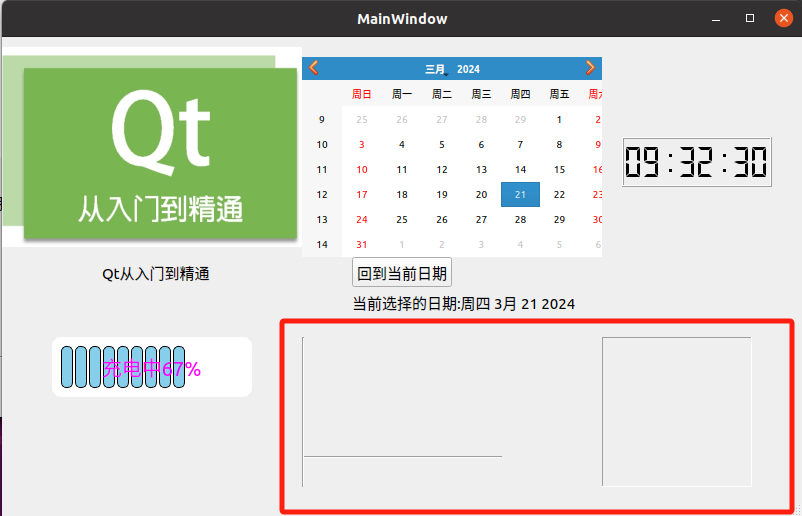
Qt教程 — 3.5 深入了解Qt 控件:Display Widgets部件(1)
目录 1 Display Widgets简介 2 如何使用Display Widgets部件 2.1 QLabel组件-显示图像或文本 2.2 QCalendarWidget组件-日历简单的使用 2.3 QLCDNumber组件-控件作时钟的显示 2.4 QProgressBar组件-模拟手机电池充电 2.5 QFrame组件-绘制水平/垂直线 Display Widgets将分…...

网络安全框架和云安全参考架构介绍
目录 一、网络安全框架 1.1 概述 1.2 IATF框架 1.2.1 框架来源 1.2.2 框架结构图 1.2.3 框架内容 1.2.3.1 人(People) 1.2.3.2 技术(Technology) 1.2.3.3 操作(Operation) 1.3 NIST网络安全框架 …...

360企业安全浏览器兼容模式显示异常某个内容不显示 偶发现象 本地无法复现情况js
360企业安全浏览器兼容模式显示异常 ,现象测试环境频发 ,本地连测试无法复现,线上反馈问题。 出现问题的电脑为windows且使用360企业安全浏览器打开兼容模式可复现 复现过程: 不直接点击超链接跳转页面 ,登录后直接通…...

JVM常见启动参数
目录 内存参数设置 垃圾收集 内存溢出 其他杂项 总结 java虚拟机(JVM)的启动参数可以用来调整其行为、性能和资源分配。以下是一些常见的JVM启动参数: 内存参数设置 初始化堆内存以满足应用程序需求是最常见的与性能相关的实践之一。 …...

单元测试、集成测试、系统测试区别
一、测方法不同 1、单元测试属于白盒测试范畴。 2、集成测试属于灰盒测试范畴。 3、系统测试属于黑盒测试范畴。 二、考察范围不同 1、单元测试主要测试单元内部的数据结构、逻辑控制、异常处理等。exception handling 2、集成测试主要测试模块之间的接口和接ロ数据传递关…...
NIVision-相机图像采集
应用场景 上位机与工业相机通讯,控制相机抓取图像。 工业相机的通讯接口大多为USB口或网口。 USB口则直接将通讯线缆插入上位机USB端口,打开MAX中设备与接口一栏可以看到电脑给相机分配的资源名称;网口则需要将网线连接相机和上位机…...
【vue-小知识】var、let 和 const之间的区别
文章目录 结论1、重复定义变量名var:允许重复定义变量名let和const:不可以重复定义变量名 2、修改值var:允许修改值let:允许修改值const:不允许修改值,会报错 3、变量提升var : 支持变量提升let和const&…...

24.3 分布式综合应用
24.3 分布式综合应用 1. 分布式事务1.1 分布式事务1.2 分布式事务方案1. 2pc2. 其他方案1.3 Seata分布式事务框架:基于2pc1. 简介2. 启动seata服务1.4 微服务事务案例分析1. 代码分析2. 基于Seata改造2. 分布式锁2.1 简介1. redis实现...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
