【LeetCode】--- 动态规划 集训(一)
目录
- 一、1137. 第 N 个泰波那契数
- 1.1 题目解析
- 1.2 状态转移方程
- 1.3 解题代码
- 二、面试题 08.01. 三步问题
- 2.1 题目解析
- 2.2 状态转移方程
- 2.3 解题代码
- 三、746. 使用最小花费爬楼梯
- 3.1 题目解析
- 3.2 状态转移方程
- 3.3 解题代码
一、1137. 第 N 个泰波那契数
题目地址: 1137. 第 N 个泰波那契数
泰波那契序列
Tn定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在n >= 0的条件下Tn+3 = Tn + Tn+1 + Tn+2
给你整数n,请返回第n个泰波那契数Tn的值。
示例 1:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
示例 2:
输入:n = 25
输出:1389537
1.1 题目解析
因为要求的是第n个泰波那契序列,所以我们可以创建一个长度为 n 的dp表,用来表示第i位置的泰波那契序列(即:dp[i]表示:第 i 个泰波那契序列的值)。
接下来便是初始化,因为 dp[i]位置是前三个数的和,所以为了后序填表时不越界,要先初始化前三个数。题目中已给出前三个值,完成初始化即可(dp[0] = 0; dp[1] = dp[2] = 1;)。
填表顺序是:从左到右,依次填表。从下标为 3 的位置开始填表。
返回值为:dp[n],即第 n 个位置的泰波那契序列的值。还需要注意的小细节是,当序列长度不足 3 时,要单独判断返回值。
1.2 状态转移方程
依据题目要求(已给出):dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
1.3 解题代码
class Solution
{
public:int tribonacci(int n) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回结束if(n == 0) return 0;if(n == 1 || n == 2) return 1;vector<int> dp(n + 1);dp[0] = 0, dp[1] = dp[2] = 1;for(int i = 3; i <= n ; ++i)dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];return dp[n];}
};
二、面试题 08.01. 三步问题
题目地址: 面试题 08.01. 三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
2.1 题目解析
为了求到第 n 级台阶的方法数,可以定义一个长度为 n+1 的dp表,dp[i]表示:到 i 位置时,一共有多少种方法。
状态转移方程的确立,因为小孩可以一次走一级,两级或三级台阶,所以他可以从第 n-1, n-2 或 n-3 级台阶上到第 n 级台阶。所以到第 n 级台阶的总方法数,是到上述三种台阶的方法数总和。(以 i 位置的状态,最近的一步,来划分问题)

接下来便是初始化,为了在填 dp 表时不越界(即取dp[i - 3]时),所以需要初始化前三个状态表的值(dp[1] = 1, dp[2] = 2, dp[3] = 4;)。还可以再多开一个位置,使台阶序号和 dp 表对应。
填表顺序:从左到右依次填表,从下标为 4 的位置开始填。
返回值:返回 dp[n],即到第 n 级台阶的方法数。在 n <= 3 时要单独判断,因为状态表从下标为 4 位置开始判断(利用最近的前三个状态)
2.2 状态转移方程
依据题目要求:dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];。还需要注意的是为了防止越界,顺应题目要求,要对结果模1000000007。那么便可写成如下格式:dp[i] = ((dp[i - 1] + dp[i - 2]) % num + dp[i - 3]) % num;
2.3 解题代码
class Solution
{
public:int waysToStep(int n) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回结束if(n == 1 || n == 2) return n;if(n == 3) return 4;vector<int> dp(n + 1);dp[1] = 1, dp[2] = 2, dp[3] = 4;int num = 1e9 + 7;for(int i = 4; i <= n; ++i)dp[i] = ((dp[i - 1] + dp[i - 2]) % num + dp[i - 3]) % num;return dp[n];}
};
三、746. 使用最小花费爬楼梯
题目地址: 746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
3.1 题目解析
此题所求的是达到楼梯顶部的最低花费,那么我们便可定义一个长度为 n+1 的 dp 状态表。多开一个是因为,此处的楼梯顶部,不是数组cost.size(),而是最后一个位置的下一个。那么我们便可使用,dp[i]来表示:到达 i 位置时,最小花费。
状态转移方程的确立,可以根据最小花费,因为一次可以向上爬一个或两个台阶。那么到达第 i 级台阶的最小花费,便可用最近的状态推导 dp[i]。即:1. 先到达 i - 1位置,然后支付cost[i - 1],走一步(dp[i - 1] + cost[i - 1]); 2. 先到达 i - 2位置,然后支付cost[i - 2],走两步(dp[i - 2] + cost[i - 2])。然后求两者最小值,这便是到达第 i 级台阶的最小费用。

初始化:为了后序填表不越界,且初始化的值不影响填表,所以可将前两个状态初始化为0(dp[0] = dp[1] = 0;)。
填表顺序:从左到右,依次填表。从下标为 2 的位置开始填。
返回值:dp[n]即是到达楼梯顶部的最低费用。
3.2 状态转移方程
依据题目要求:dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i -2]);
3.3 解题代码
class Solution
{
public:int minCostClimbingStairs(vector<int>& cost) {//1. 创建dp表//2. 初始化//3. 填表//4. 返回结束int n = cost.size();vector<int> dp(n + 1);dp[0] = 0, dp[1] = 0;for(int i = 2; i <= n; ++i)dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);return dp[n];}
};
相关文章:

【LeetCode】--- 动态规划 集训(一)
目录 一、1137. 第 N 个泰波那契数1.1 题目解析1.2 状态转移方程1.3 解题代码 二、面试题 08.01. 三步问题2.1 题目解析2.2 状态转移方程2.3 解题代码 三、746. 使用最小花费爬楼梯3.1 题目解析3.2 状态转移方程3.3 解题代码 一、1137. 第 N 个泰波那契数 题目地址:…...
【数据结构与算法】(18):树形选择排序:按照锦标赛的思想进行排序
🤡博客主页:Code_文晓 🥰本文专栏:数据结构与算法 😻欢迎关注:感谢大家的点赞评论关注,祝您学有所成! ✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看&…...

统计单词数
统计单词数 题目描述 一般的文本编辑器都有查找单词的功能,该功能可以快速定位特定单词在文章中的位置,有的还能统计出特定单词在文章中出现的次数。 现在,请你编程实现这一功能,具体要求是:给定一个单词࿰…...

c++pair的用法
pair简单来说就是可以存储两种类型数据的一个类,其内部是使用模板实现的,所以可以指定其内部的类型。 pair在#include <utility> pair的构造 pair<int, string> p1({ 1,"张三" });pair<int, string> p2;pair<int, str…...

石油炼化5G智能制造工厂数字孪生可视化平台,推进行业数字化转型
石油炼化5G智能制造工厂数字孪生可视化平台,推进行业数字化转型。在石油炼化行业,5G智能制造工厂数字孪生可视化平台的出现,为行业的数字化转型注入了新的活力。石油炼化行业作为传统工业的重要领域,面临着资源紧张、环境压力、安…...

IP代理技术革新:探索数据采集的新路径
引言: 随着全球化进程不断加深,网络数据采集在企业决策和市场分析中扮演着愈发重要的角色。然而,地域限制和IP封锁等问题常常给数据采集工作带来了巨大挑战。亿牛云代理服务凭借其强大的网络覆盖和真实住宅IP资源,成为解决这些问…...
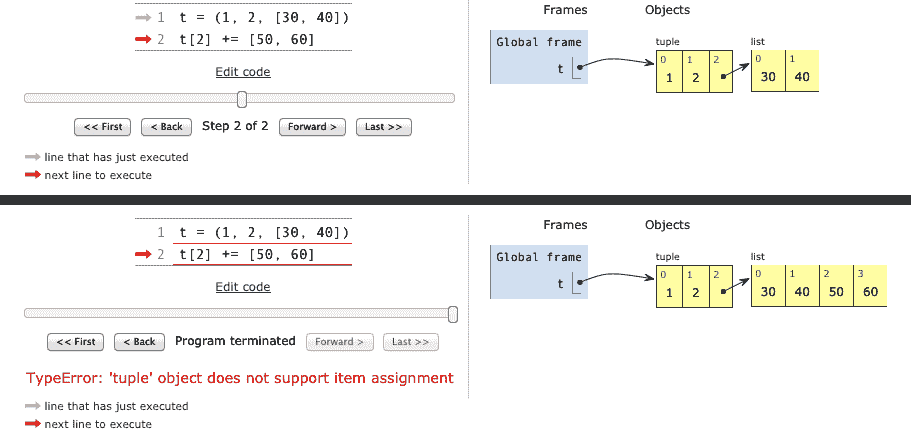
流畅的 Python 第二版(GPT 重译)(一)
前言 计划是这样的:当有人使用你不理解的特性时,直接开枪打死他们。这比学习新东西要容易得多,不久之后,活下来的程序员只会用一个容易理解的、微小的 Python 0.9.6 子集来编写代码 。 Tim Peters,传奇的核心开发者&am…...

Vue+jquery+jquery.maphilight实现图片热区高亮以及点击效果
//鼠标悬浮效果 mounted() {this.setCurrentTask(0); //对于id为mapAll的热区图,设置鼠标放置在上面有一个颜色 fillColor填充颜色 strokeColor边框颜色 strokeWidth边框宽度 fillOpacity 是设置热区填充颜色的不透明度的属性。 alwaysOn:true 保持常量$(function(…...

靠谱!朋友圈一键转发和自动转发好友朋友圈
微信朋友圈在生活和工作中扮演着重要的社交和信息传播角色。尤其是对于一些企业来说,朋友圈是不可或缺的推广渠道。 今天就给大家分享一个能够实现一键转发和自动转发好友朋友圈的工具——微信管理系统,让大家都能有效的管理朋友圈。 1、定时发圈&…...

线性顺序表算法库
list.cpp 具体函数实现 #include <stdio.h> #include "list.h" #include <malloc.h>/************************************************** ①函数名: CreateList 功 能: 用数组构建顺序表 参 数: ①SqList *&L:传入的线性表 ②ElemType a[]:使用…...

java分割等和子集(力扣Leetcode416)
分割等和子集 力扣原题链接 给你一个只包含正整数的非空数组nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] …...

383. 赎金信
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。 func canConstruct(ransomNote …...

【二】【单片机】有关独立按键的实验
自定义延时函数Delay 分别用Delay.c文件存储Delay函数。用Delay.h声明Delay函数。每次将这两个文件复制到工程中,直接使用。 //Delay.c void Delay(unsigned int xms) //11.0592MHz {while(xms--){unsigned char i, j;i 2;j 199;do{while (--j);}…...

AJAX踩坑指南(知识点补充)
JWT JSON Web Token是目前最为流行的跨域认证解决方案 如何获取:在使用JWT身份验证中,当用户使用其凭据成功登录时,将返回JSON Web Token(令牌) Token本质就是一个包含了信息的字符串 如何获取Token:登录成功之后,服务…...

备战蓝桥杯Day29 - 拼接最大数字问题
问题描述 有n个非负整数,将其按照字符串拼接的方式拼接为一个整数如何拼接可以使得得到的整数最大? 例: 32,94,128,1286,6,71可以拼接除的最大整数为 94716321286128。 问题思路 1.比较两个字符串的第一个数字,数值大的在前面,数值小的在…...
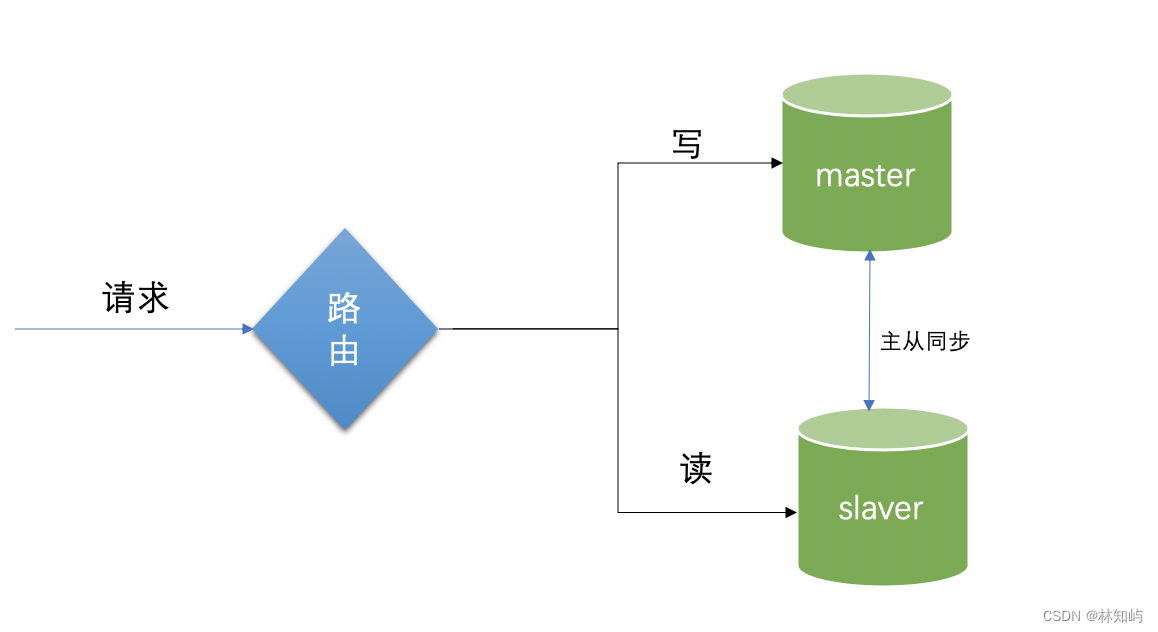
基于springboot的mysql实现读写分离
前言: 首先思考一个问题:在高并发的场景中,关于数据库都有哪些优化的手段?常用的有以下的实现方法:读写分离、加缓存、主从架构集群、分库分表等,在互联网应用中,大部分都是读多写少的场景,设置两个库,主库和读库,主库的职能是负责写,从库主要是负责读…...

Python爬虫之Scrapy框架系列(24)——分布式爬虫scrapy_redis完整实战【XXTop250完整爬取】
目录: 每篇前言:1.使用分布式爬取豆瓣电影信息(1)settings.py文件中的配置:(2)spider文件的更改:(3)items.py文件(两个项目一致!&…...
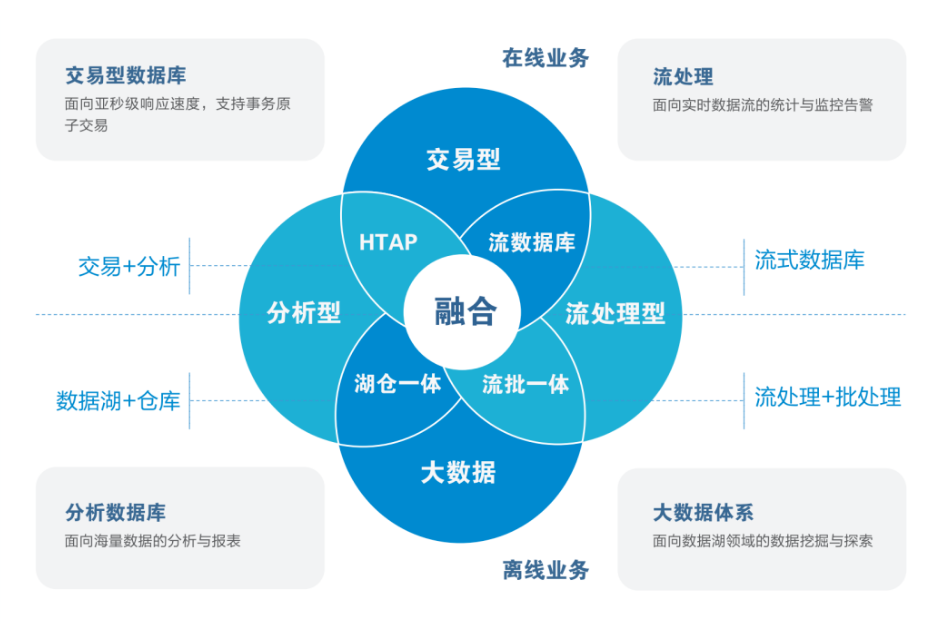
提升效率,稳定可靠:亚信安慧AntDB的企业价值
亚信安慧AntDB分布式数据库凭借平滑扩展、高可用性和低成本三大核心优势,在业界获得了极高的评价和认可。这些优点不仅为AntDB提供了巨大的市场发展潜力,也使其成为众多企业在数据管理上的首选解决方案。 AntDB的平滑扩展特性极大地提升了企业的灵活性和…...

洛谷入门——P1567 统计天数
统计天数 题目描述 炎热的夏日,KC 非常的不爽。他宁可忍受北极的寒冷,也不愿忍受厦门的夏天。最近,他开始研究天气的变化。他希望用研究的结果预测未来的天气。 经历千辛万苦,他收集了连续 N ( 1 ≤ N ≤ 1 0 6 ) N(1 \leq N …...
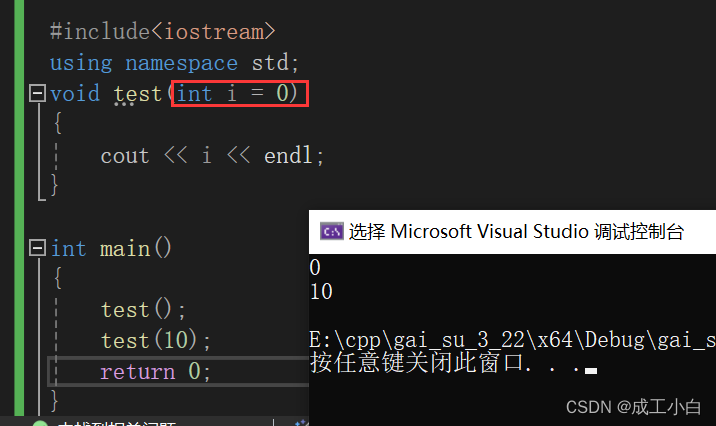
C++概述
目录 一、C关键字(63个) 二、C几个关键点: 三、C语言缺陷一:命名冲突 四、C新概念:命名空间(namespace) 五、命名空间的嵌套: 六、展开命名空间:(using …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
