Bellman-ford和SPFA算法
目录
一、前言
二、Bellman-ford算法
1、算法思想
2、算法复杂度
3、判断负圈
4、出差(2022第十三届国赛,lanqiaoOJ题号2194)
三、SPFA算法:改进的Bellman-Ford
1、随机数据下的最短路问题(lanqiaoOJ题号1366)
一、前言
本文主要讲了 Bellman-ford 和 SPFA 算法概念和相应例题。
二、Bellman-ford算法
- 单源最短路径问题:给定一个起点 s,求它到图中所有 n 个结点的最短路径。
1、算法思想
- 图中每个点上站着一个 “警察”。
- 每个警察问邻居:走你这条路能到 s 吗?有多远?
- 反复问多次,最后所有警察都能得到最短路。
- 第1轮,给所有 n 个人每人一次机会,问他的邻居,到 s 的最短距离是多少?更新每人到 s 的最短距离。特别地,在 s 的直连邻居中,有个 t,得到了到 s 的最短距离。(注意,算法并没有查找是哪个 t)
- 第2轮,重复第 1 轮的操作。
更新每人到 s 的最短距离。
特别地,在 s 和 t 的直连邻居中,有个 v,得到了到 s 的最短距离。
- 第3轮,……
2、算法复杂度
- 一共需要几轮操作?每一轮操作,都至少有一个新的结点得到了到 s 的最短路径。所以,最多只需要 n 轮操作,就能完成 n 个结点。
- 在每一轮操作中,需要检查所有 m 个边,更新最短距离。
- Bellman-Ford算法的复杂度: O(nm)。
3、判断负圈
- Bellman-Ford 能判断负圈。
- 没有负圈时,只需要n轮就结束。
- 如果超过n轮,最短路径还有变化,那么肯定有负圈。
4、出差(2022第十三届国赛,lanqiaoOJ题号2194)
【题目描述】
A国有 N 个城市,编号为 1...N,小明是编号为 1 的城市中一家公司的员工,需要去编号为 N 的城市出差。由于疫情原因,小明无法乘坐飞机直接从城市 1 到达城市 N,需要通过其他城市进行陆路交通中转。小明通过交通信息网,查询到了 M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。由于疫情原因,小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络,小明也查询到了各个城市的隔离信息。(小明之前在城市 1,可以直接离开城市 1,不需要隔离)小明希望能够尽快赶到城市 N,你帮他规划一条路线,能够在最短时间内到达城市 N。
【输入】
第1行:两个正整数 N, M,N 表示 A 国的城市数量,M 表示未关闭的路线数量。第2行:N 个正整数,第 i 个整数 Ci 表示到达编号为 i 的城市后需要隔离的时间。第 3 ... M+2 行:每行 3 个正整数, u, v, c 表示有一条城市 u 到城市 v 的双向路线仍然开通着,通过该路线的时间为 c。
【输出】
第1行:1 个正整数,表示小明从城市 1 出发到达城市 N 的最短时间 (到达城市 N,不需要计算城市 N 的隔离时间)。
对于 100% 的数据,1≤N≤1000,1≤M≤10000,1≤Ci≤200, 1≤u, v≤N, 1≤c≤1000
【样例输入】
4 4
5 7 3 4
1 2 4
1 3 5
2 4 3
3 4 5
【样例输出】
13
思考:
- 本题求最短路径,数据规模 1≤N≤1000, 1≤M≤10000 不算大。
- 用什么算法?本题是单源最短路径问题。用复杂度 O(n^3) 的多源最短路算法 floyd 算法超时;用复杂度 O(mn) 的单源最短路 Bellman-ford 算法正好;
- 没有必要使用更好的 Dijkstra 和 SPFA 算法。两点之间的边长,除了路线时间 c,还要加上隔离时间。经过这个转化后,本题是一道简单的 Bellman-ford 算法模板题。
n,m=map(int,input().split()) #n:城市。m:路线
c=[0]+[int(i) for i in input().split()] #隔离时间
#G=[[0]*(n+1) for i in range(n+1)]
e=[] #存每一条边
for i in range(m):u,v,w=map(int,input().split())e.append((u,v,w))e.append((v,u,w)) #双向边,没有的话会报错
INF=1<<64
dis=[INF]*(n+1)
dis[1]=0
for k in range(1,n+1): #n个点,执行n轮问路for u,v,w in e:res=c[v]if v==n:res=0dis[v]=min(dis[v],dis[u]+w+res)
print(dis[n])
可惜该题解还是会部分超时。
三、SPFA算法:改进的Bellman-Ford
- SPFA=队列处理+ Bellman-Ford。
- Bellman-Ford算法有很多低效或无效的操作。其核心内容,是在每一轮操作中,更新所有结点到起点s的最短距离。
- 计算和调整一个结点u到s的最短距离后,如果紧接着调整u的邻居结点,这些邻居肯定有新的计算结果;而如果漫无目的地计算不与u相邻的结点,很可能毫无变化,所以这些操作是低效的。
- 改进:计算结点u之后,下一步只计算和调整它的邻居,能减少计算。
- 这些步骤用队列进行操作,这就是SPFA。
SPFA步骤:
1)起点 s 入队,计算它所有邻居到 s 的最短距离。把 s 出队,状态有更新的邻居入队,没更新的不入队。
2)现在队列的头部是 s 的一个邻居 u。弹出 u,更新它所有邻居的状态,把其中有状态变化的邻居入队列。
3)继续以上过程,直到队列空。这也意味着,所有结点的状态都不再更新。最后的状态就是到起点 s 的最短路径。
SPFA不稳定:
- 弹出 u 之后,在后面的计算中,u 可能会再次更新状态 (后来发现,u 借道别的结点去 s,路更近)。所以,u 可能需要重新入队列。
- 有可能只有很少结点重新进入队列,也有可能很多。这取决于图的特征。
- 所以,SPFA 是不稳定的。
1、随机数据下的最短路问题(lanqiaoOJ题号1366)
【题目描述】
给定 N 个点和 M 条单向道路,每条道路都连接着两个点,每个点都有自己编号,分别为 1~ N。问你从 S 点出发,到达每个点的最短路径为多少。
【输入描述】
输入第一行包含三个正整数 N, M, S。第 2 到 M+1 行每行包含三个正整数 u, v, w,表示 u→v 之间存在一条距离为 w 的路。1≤N≤5×10^3,1≤M≤5×10^4,1≤ui, vi≤N,0≤wi≤10^9
【输出描述】
输出仅一行,共 N 个数,分别表示从编号 S 到编号为 1~ N 点的最短距离,两两之间用空格隔开。(如果无法到达则输出-1)
import heapq
def spfa(s):dis[s]=0hp=[]heapq.heappush(hp,s) #用heapq处理优先队列inq=[0]*(n+1) #标志某一点是否已访问inq[s]=1 while hp:u=heapq.heappop(hp)inq[u]=0if dis[u]==INF:continuefor v,w in e[u]: #遍历点u的邻居v,边长为wif dis[v]>dis[u]+w:dis[v]=dis[u]+wif inq[v]==0:heapq.heappush(hp,v)inq[v]=1n,m,s=map(int,input().split())
e=[[] for i in range(n+1)]
INF=1<<64
dis=[INF]*(n+1)
for _ in range(m):u,v,w=map(int,input().split())e[u].append((v,w)) #u的邻居是v,边长是w
spfa(s)
for i in range(1,n+1):if dis[i]>=INF:print("-1",end=' ')else:print(dis[i],end=' ')
另外,spfa也能判断负环。
Neq[i]:表示一个任意点 i 进队列的次数,如果大于 n 次,就出现了负环。
补充:
【SPFA的简单优化】
SPFA 算法的主要操作是把变化的点放进队列。这些点差不多是随机放进队列的,如果改变进队和出队的顺序,是否能加快所有点的最短路计算?下面是两个小优化。
1)进队的优化:SLF (Small Label First)
需要使用双端队列 deque。
队头出队后,需要把它的有变化的邻居放进队列。把进队的点 u 与新队头 v 进行比较,如果 dis[u] < dis[v],将 u 其插入到队头,否则插入到队尾。这个优化使得队列弹出的队头都是路径较短的点,从而加快所有点的最短路的计算。
2)出队的优化:LLL (Large Label Last)
计算队列中所有点的 dis 的平均值 x,每次选一个小于 x 的点出队。具体操作是:如果队头 u 的dis[u] > x,把 u 弹出然后放到队尾去,然后继续检查新的队头 v,直到找到一个 dis[v]<x 为止。这个优化也是先处理了更短的点。
【比较 Bellman-ford 算法和 Dijkstra 算法】
Dijkstra 算法是一种 “集中式” 算法,Bellman-ford 算法是一种“分布式”算法。图上有 n 个点,假设每个点上都有一台独立的计算机,现在让每个点计算它到其他所有点的最短路,两种算法的特点分别是:
1)Dijkstra 算法。计算一个起点 s 到其他所有点的最短路,是以 s 为中心点扩散出去,对其他所有点进行的计算都是围绕着起点 s 的,复杂度 O(m×logn)。每个点上的计算机独自做自己的计算,不管其他点的计算结果。Dijkstra 算法是一种 “集中式” 算法,点与点之间 “独立计算,互不干涉”。
2)Bellman-ford 算法。对任意一个点来说,它需要做的只是逐个询问它的所有邻居:有没有到其他点的更短的路?如果有则更新,并把这个更新告诉它的其他邻居,以方便这些邻居也做更新。经过 n 轮询问,就得到了它到其他所有点的最短路。设一个点平均有 10 个邻居,那么这个点上的计算机只需做 10×n 次计算,就能确定它到图中其他所有点的最短路。Bellman-ford 算法是一种 “分布式” 计算,点与点之间通过互相交换信息来计算最短路径,可以概况为 “合作计算,互通有无”。
Bellman-ford 的复杂度是 O(m×n),比 Dijkstra 的 O(m×logn) 差,这是在单机上。如果是并行计算,每个点单独计算,Bellman-ford 比 Dijkstra 算法的效率更高,计算也更简单。
以上,Bellman-ford和SPFA算法
祝好
相关文章:
Bellman-ford和SPFA算法
目录 一、前言 二、Bellman-ford算法 1、算法思想 2、算法复杂度 3、判断负圈 4、出差(2022第十三届国赛,lanqiaoOJ题号2194) 三、SPFA算法:改进的Bellman-Ford 1、随机数据下的最短路问题(lanqiaoOJ题号1366&…...

假如你知道这样的MySQL
数据库三范式是什么? 第一范式(1NF):字段具有原子性,不可再分。(所有关系型数据库系 统都满足第一范式数据库表中的字段都是单一属性的,不可再分)第二范式(2NF)是在第一范式(1NF)的…...
SpringBoot笔记(一)入门使用
一、为什么用SpringBootSpringBoot优点创建独立Spring应用内嵌web服务器自动starter依赖,简化构建配置自动配置Spring以及第三方功能提供生产级别的监控、健康检查及外部化配置无代码生成、无需编写XMLSpringBoot缺点人称版本帝,迭代快,需要时…...
C++20 协程体验
1 介绍协程是比线程更加轻量级并发编程方式,CPU资源在用户态进行切换,CPU切换信息在用户态保存。协程完成异步的调用流程,并对用户展示出同步的使用方式。协程的调度由应用层决定,所以不同的实现会有不同的调度方式,调度策略比较灵…...

这三个小事你做HIGG FEM时要知道
【这三个小事你做HIGG FEM时要知道】1.为什么做了Higg FEM 自评后要做验证?「自评 验证」Higg FEM 是一个持续改善的框架方法,来帮助工厂实现持续的环保改善,是一个最基本的要求,如果工厂期望得到一个更加客观的评价,…...

.net6 wpf程序一个内存不断增长问题的解决方法
一个.net6的应用程序,底层不断采集数据。使用wpf制作了一个简单的界面显示数据接收的情况。程序中引用了 Material Design UI框架。当程序长时间运行时发现内存在不断增长。一个星期后工作集占用内存达到1GB。使用dotnet-dump工具收集内存使用情况,并且分…...
NICEGUI---ROS开发之中常用的GUI工具
0. 简介 对于ROS来说,如果不具备一定知识的人员来使用这些我们写的算法,如果说没有交互,这会让用户使用困难,所以我们需要使用GUI来完成友善的数据交互,传统的GUI方法一般有PYQT这类GUI方法,但是这类GUI工…...

高盐废水除钙镁的技术解析
高盐废水指含有机物和至少总溶解固体(totaldissolvedsolids,tds)的质量分数大于3.5%的废水,具有水量大,无机盐离子k、na、ca2、mg2、cl-、so42-等含量高,水质水量变化大,成分复杂,难生化降解等特…...

回文日期门牌制作
题目: 题目描述 如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202,恰好是一个回文数。我们称这样的日期是回文日期。20200202 并不仅仅是一个回文日期,还是一个 ABABBABA 型的回文日期。 给定一个 8 位数的日期,请…...
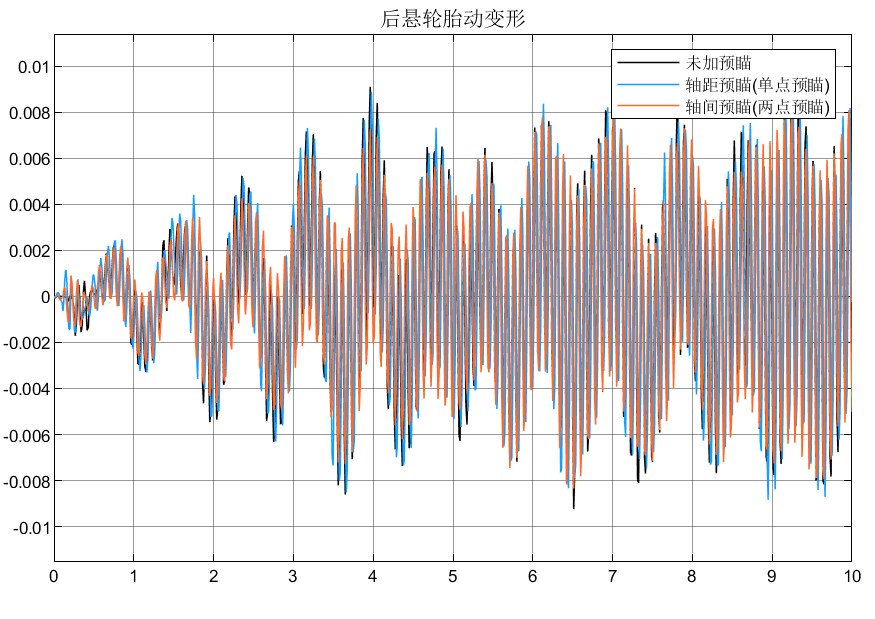
基于半车悬架的轴距预瞄与轴间预瞄仿真对比
目录 前言 1. 半车悬架模型 2.轴距预瞄(单点预瞄)和轴间预瞄(两点预瞄)原理与仿真分析 2.1轴距预瞄(单点预瞄) 2.1.1预瞄原理 2.2.轴间预瞄(两点预瞄) 2.2.1预瞄原理 2.3仿真分析 3.总结 前言 对于悬架而言,四个车轮实际的输入信息是受到前后延时以及左右相…...

Linux开发 安装JDK8、p4
前面的笔记: Linux 学习笔记1 安装linux详细教程_linux系统 setting_O丶ne丨柒夜的博客-CSDN博客 Linux 学习笔记2 常用命令_O丶ne丨柒夜的博客-CSDN博客 Linux 学习笔记3 权限管理 定时任务 网络配置_O丶ne丨柒夜的博客-CSDN博客 安装配置 安装配置JDK8 Java …...

基于 x86 SoC 的车辆智能驾驶舱和ADAS设计(一)
随着汽车成为软件定义的自动化领域的中心,英特尔致力于提供从汽车到云的可扩展安 全解决方案来加快从高级驾驶员辅助系统(ADAS)到全自动汽车为自动驾驶提供技术支持。 2016 年 3 月,英特尔斥资 153 亿美元收购了以色列高级辅助驾驶系统企业 Mobileye。20…...

类模板函数模板
准备看个项目找实习,边看边学,一看到处都是template 和typename,好几年前学的C都忘记光了,在这里先做个笔记复习一下。template <class T> T abs(T x) {if(x < 0) return -x;return x; } int main() {int x 1;cout <…...

Leetcode DAY 56: 两个字符串的删除操作 and 编辑距离
583. 两个字符串的删除操作 1 、 dp[i][j] 表示 让以word1[i - 1]为结尾的字符串 和 以word2[i - 2]为结尾的字符串 相等需要删除的最少次数 1、dp[i][j] 的 递推需要考虑两种情况: (1)word1[i - 1] word2[j - 1] 相当于不考虑word1[i]和…...

系统检测维护工具Wsycheck使用(18)
实验目的 (1)学习Wsycheck的基本功能; (2)掌握Wsycheck的基本使用方法; 预备知识 windows操作系统的基本知识如:进程、网络、服务和文件等的了解。 Wsycheck是一款强大的系统检测维护工具,进程和…...

111 ok
全部 答对 答错 单选题 1.在与团队一起召开开工会议之后,项目经理分配工作活动,由于与其职能经理分配的任务发生冲突,一位团队成员拒绝开始工作,项目经理首先应该做什么? A请项目发起人帮助与职能经理进行谈判 B签发…...

Python API教程:API入门
什么是API? 一个API,或被称为应用程序接口,是一个服务器为你提供一个接收或发送数据的代码。API通常用来接收数据。 本文就集中焦点在此话题中。 当我们想从一个API中接收数据,我们需要开始请求。请求可以包含整个Web。例如&am…...
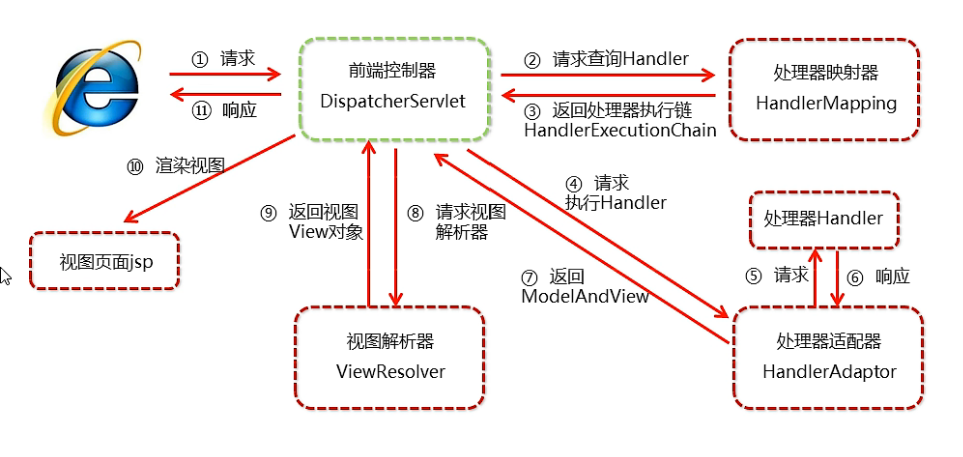
SpringMVC学习笔记
文章目录一、SpringMVC简介1、MVC与三层架构1.1 M1.2 V1.3 C1.4 MVC模式的工作流程1.5 三层架构2、什么是SpringMVC3、SpringMVC的特点二、搭建项目框架1、web项目结构2、创建maven工程,配置pom.xmla>添加web模块b> pom.xml中设置打包方式:warc>…...

Linux学习记录01
文章目录1. Linux基础知识2. Linux常用命令2.1 基础知识2.2 ls命令2.3 cd pwd命令2.4 mkdir2.5 touch、cat、more2.6 cp、mv、rm2.7 通配符、root模式2.8 whicih、find命令2.9 grep、mc、| 管道符2.10 echo、反引号、tail、重定向符2.11 vi、vm文本编辑器1. Linux基础知识 Lin…...
VScode 插件【配置】
写这篇博客的原因: vscode 很久以前的插件,忘记是干什么的了记录 vscode 好用的插件 插件介绍(正文开始) Auto Rename tag 开始/关闭标签内容 同步 Chinese (Simplified) VScode 中文化 CSS Peek 通过 html 代码查找到引用的样式…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...

