第十二届蓝桥杯省赛CC++ 研究生组
十二届省赛题
第十二届蓝桥杯省赛C&C++ 研究生组-卡片
第十二届蓝桥杯省赛C&C++ 研究生组-直线
第十二届蓝桥杯省赛C&C++ 研究生组-货物摆放
第十二届蓝桥杯省赛C&C++ 研究生组-路径
第十二届蓝桥杯省赛C&C++ 研究生组-时间显示
第十二届蓝桥杯省赛C&C++ 研究生组-砝码称重
第十二届蓝桥杯省赛C&C++ 研究生组-异或数列
第十二届蓝桥杯省赛C&C++ 研究生组-双向排序
三年小小结
水过了最新三年的题目,小小复盘一下~
简单模拟
-
卡片(填空):从1开始计算每位所用卡片,当某个数字的卡片不足时,则找到能拼到的最大数。注意最后的这个数是拼不出来的第一个数,所以答案记得减一。作为填空题,枚举即可解决,该题目进一步思考的话,一定是卡片1消耗量最大,可转化为1出现2021次的数字
-
直线(填空):判断给定范围内的点能组成多少条不同直线,表面考算法,其实是考数学公式~注意分母不为0,直接把平行于y轴的单算即可,记得后续加上。

-
时间显示:常见的时间处理类问题,小小注意下小时是24小时制。需要显示的时间是时(0-23)分(0-59)秒(0-59),给的输入是从00-00-00开始的毫秒数,则该先除的先除该求余的求余。给的年份就是迷惑性信息了,木用,忽略即可。
-
裁纸刀(填空):先裁四下去掉边缘,再把行分开(行数-1),再把列分开((列数-1)*行数)。甚至都没啥小坑,温柔
-
灭鼠先锋(填空):手动可以直接模拟~ 再优化一点点的话,对于一行空内容的话,谁先手谁必输,问题等价于谁后把第一行填满,谁就一定能保证自己赢。问题分解的思想很有效,简单分割也许就能大幅简化问题
-
与或异或(填空):电路图看起来挺唬人的,但枚举就能解决的纸🐅。本质上就是按照a[i][j] = a[i-1][j] op a[i-1][j+1],其中op可选&、^、|其一,统计结果为1的组合个数。
-
翻转:翻转规则为出现010或101就可以把中间的值翻转,借助翻转的情况下是否能把两个串变相同,如果是输出最小翻转次数。虽然题设中有“翻转操作可无限重复”,但其实一次翻转即可,翻完了其实也就不能出现不同了,属于干扰信息。以s串1010101为例,翻转第一次1000101,翻转第二次1000111,搞定。
excel
- 工作时长(填空):本质上要求的是两个时间段之差的和。用excel先排序;再选择时间格式[h]:mm:ss,注意小时的选择,以处理超出24小时的情况;计算两个时间段的差,关于求出整列的上下行间的时间差,先手算两个单元格,后续直接下拉即可自动计算;求和
数学问题
质因数
很稳定,每年都考了一个,或直接或加了点马甲
- 货物摆放(填空):整数分解问题。n较大直接暴力枚举不可行,考虑当时质因数模块学过整数范围内一定能用十个质因数表示,类推n的约数也不会太多,转化为先求出n的约数(别漏了1和n),再计算相乘为n的组合个数
- 质因数个数:给出整数n的质因数个数
sqr = sqrt(1.0*n);
num = 0;
for(int i = 2; i <= sqr; i++){if(n % i == 0){num++;while(n % i == 0) n /= i;}
}
if(n > 1) num++;//别漏了最后这个顽固分子~
- 公因数匹配:找到首次出现或同时出现但最短的区间,满足头尾元素有大于1的公因数。直接暴力的话两层的105超时,有了之前的经验,也考虑下先分解看看。分解每个数的所有质因数,如果没出现过,则记录首次出现的位置;如果已经出现过,判断是否需要更新最左位置。判断该数满足的区间是否早于或短于已有的区间,若是则更新。
#include<stdio.h>
#include<math.h>
const int maxn = 1e6 + 10;
int p[maxn] = {0};
int main(){int n, x, l, ansL, ansR = 0, sqr;scanf("%d", &n);ansL = n + 1;for(int i = 1; i <= n; i++){l = n + 1;scanf("%d", &x);sqr = sqrt(1.0 * x);for(int j = 2; j <= sqr; j++){if(x % j == 0){if(!p[j]) p[j] = i;else if(p[j] < l) l = p[j];while(x % j == 0) x /= j;}}if(x > 1){if(!p[x]) p[x] = i;else if(p[x] < l) l = p[x];}if(l < ansL || (ansL == l && ansR > i)){ansL = l;ansR = i;}}printf("%d %d", ansL, ansR);return 0;
}
说都说了,顺带复习下最小公约数&最大公倍数
int gcd(int a, int b){//辗转相除法求最大公约数,时间复杂度O(logn) if(!b) return a;return gcd(b, a % b);
}最小公倍数为a * b / gcd(a, b)
- 数的拆分:给出整数n,将其拆分为x2* y3(大于2和偶数次幂可以转化为底数先升幂再把幂次调到2,奇数次幂同理,例如x4=x2的平方,y5=y2的平方 *y)的形式则可拆分返回yes,否则返回no。n最大为10e18,开五次方大约是4000,则我们对4000以内的质数打表,分解后的约数就不会太大了。判断是否能够融入我们要求的模式,即能否转化为平方或立方,能则该数可以拆分,否则是个单蹦不能拆分。
进制转换
- 异或数列:十进制转二进制。各方初始值为0,给定数列,选数异或,每个数只能选用一次。显然,谁先抢到最高位的“唯一”(1个或奇数的单蹦1)一个1则必胜。问题转化为寻找:
- 最高位的唯一的一个1
- 最高位的偶数个1
- 总的零的数量为偶数个,先手拿到单蹦1则必胜
- 总的零的数量为奇数个,后手拿到单蹦1则必胜
否则为平局
2.
阶乘特点
- 阶乘的和:直接算的话肯定超时,而且仔细想来只是求最大的m,并不需要真的算出和,只是能进行比较即可,算出来也是多余工作。回到问题本身阶乘m!,我们有多个ai!,对于多个阶乘有(m+1)m! = (m+1)!,我们对ai进行排序,顺带统计每个数的出现次数,要有序且有映射关系考虑用map;自底到高统计每位是否能进位,第一个不能进位前的数就是我们要找的m
求余
- GCD:考查辗转相除法和求余的简化。思维更简单的解法,观察知最大公约数是abs(a-b),从1开始依次枚举即可,能骗些分数。进一步思考的话,回到问题本身,
- 找使得gcd(a+k,b+k)最大的k,根据辗转相除算法知,gcd(a+k,b+k)=gcd(b+k,b-a)
- gcd(b+k,b-a) = b-a(假设已经处理好,能保证b >= a)
- 转化为找到满足(b+k)%(b-a) == 0的最小值
- 记g = b- a,则(b+k)%g = (b % g + k % g) % g == 0
b % g <g, k % g < g,则g - b % g = k

#include<iostream>
#include<algorithm>
using namespace std;
int main(){long long a, b, g;scanf("%lld%lld", &a, &b);if(a > b) swap(a, b);g = b - a;printf("%lld", g - b % g);return 0;
}
观察规律
- 全排列的价值:观察给出的样例知,对于1~n, 前后两两价值相加的和都相等,为(n-1)*n/2;那再看可以组数,也就是排列数n!/2(除2是因为两两一组相加才为定值)

动态规划
- 砝码称重:很经典的一个问题。我们能称出来的最大重量是所有砝码重量之和,最小的可能重量是1,其中题设告诉我们砝码总重范围也是一种暗示了。
利用dp的话,我们依次计算有1~n个砝码能称出来的重量,首先前i个砝码能称出来的重量,也一定能用前i+1个砝码称出来。对于前i个砝码的判断,之前称不出来的重量m,考虑- 第i个砝码重量w[i] == m
- 已经可以称出来m + w[i]
- 已经可以称出来abs(m - w[i])
- m > w[i],能称出来m-w[i],则再加个w[i]
- w[i] < m,能称出来w[i]-m,则在对面来个w[i]
最后统计用n个砝码所能称出的重量个数即可
int dp[N][maxn] = {0};
count = 0;
for(int i = 1; i <= n; i++){for(int j = 1; j <= sum; j++){dp[i - 1][j] = 1;if(!dp[i][j]){if(w[i] == j || a[i - 1][j + w[i]] || a[i - 1][abs(j - w[i])]) dp[i][j] = 1;}}
}for(int i = 1; i <= sum; i++)count += dp[n][i];
莫队算法
- 重复的数:很直给的一个莫队情况,大致思想是首先只适用于可离线的情况,对元素进行分块,对查询区间排序(同块则按照右边界排序,不同块按照块号排序);处理查询
m叉树
- 子树的大小:
- 对于m叉树的第i个结点,第一个结点号为(i - 1) * m + 2
- 满m叉树时,第i个结点的最右孩子为i*m + 1(这个1是根节点)
- 总结点数为n的完全m叉树,最后一个分支节点的最右孩子为n
相关文章:

第十二届蓝桥杯省赛CC++ 研究生组
十二届省赛题 第十二届蓝桥杯省赛C&C 研究生组-卡片 第十二届蓝桥杯省赛C&C 研究生组-直线 第十二届蓝桥杯省赛C&C 研究生组-货物摆放 第十二届蓝桥杯省赛C&C 研究生组-路径 第十二届蓝桥杯省赛C&C 研究生组-时间显示 第十二届蓝桥杯省赛C&C 研究生组…...

Ubuntu自启GUI程序
问题描述 最近搞了一个项目,程序需要自动启动,系统是Ubuntu,先搞了成服务方式(配置的文章很多,可以自己找找),程序还是不启动 ,最后加到/etc/rc.local文件里面启动,看调试信息,需要…...

【光标精灵】让您享受鼠标皮肤多样化快捷更换
鼠标作为我们日常使用频率最高的“小伙伴”,扮演着至关重要的角色。尤其是在女生群体中,对于打造一个个性化、可爱的电脑桌面和软件界面的需求日益增长。然而,尽管电脑默认提供了一些可更换的光标图案,但仍显得有些单调和呆板。想…...
)
Vue 常见面试题(一)
目录 1、Vue 的最大的优势是什么?(必会) 2、Vue 和 jQuery 两者之间的区别是什么?(必会) 3、MVVM 和 MVC 区别是什么?哪些场景适合?(必会) 1、基本定义 2…...

Elasticsearch 的 scroll API
对于大量数据,可以使用 Elasticsearch 的 scroll API 来分批次地读取数据,以避免一次性读取所有数据造成的内存负担。这段代码使用滚动查询(scroll)来分批次地读取数据。首先,它发送初始的搜索请求,并获取第…...

Leedcode刷题——2 字符串
注:以下代码均为c 1. 反转字符串 void reverseString(vector<char>& s) {int n s.size();int i, j;for(i 0, j n - 1; i < j; i, j--){swap(s[i], s[j]);}}2. 整数反转 int reverse(int x) {int rev 0;while(x ! 0){if(rev < INT_MIN / 10 || …...

2016年认证杯SPSSPRO杯数学建模B题(第二阶段)多帧图像的复原与融合全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 B题 多帧图像的复原与融合 原题再现: 数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 64&#x…...
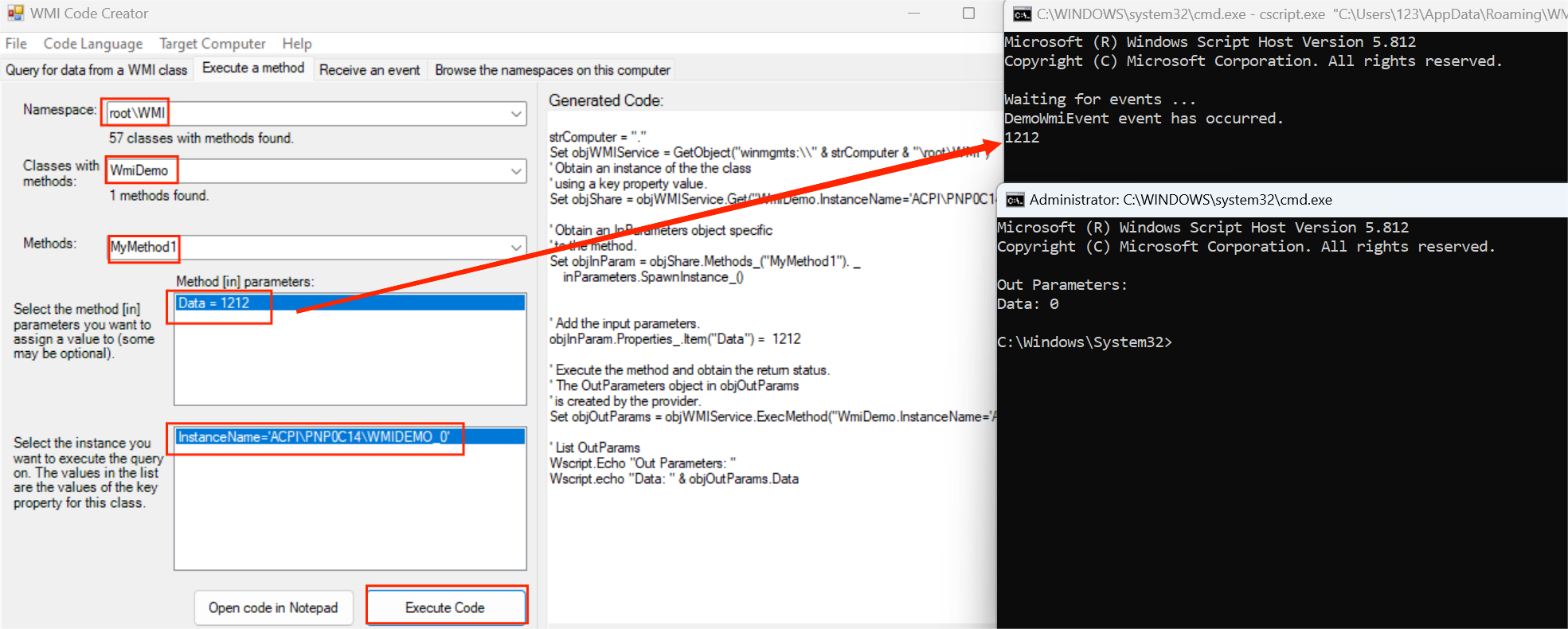
WMI接口设计实现
WMI是Windows操作系统管理数据和操作的基础设施,系统管理员可以使用VB Script、PowerShell及Windows API(C、C#等)管理本地或远程计算机。 使用WMI框架应用程序可以直接访问EC RAM、 I/O端口、Memory地址、寄存器、Setup NV设定值,…...
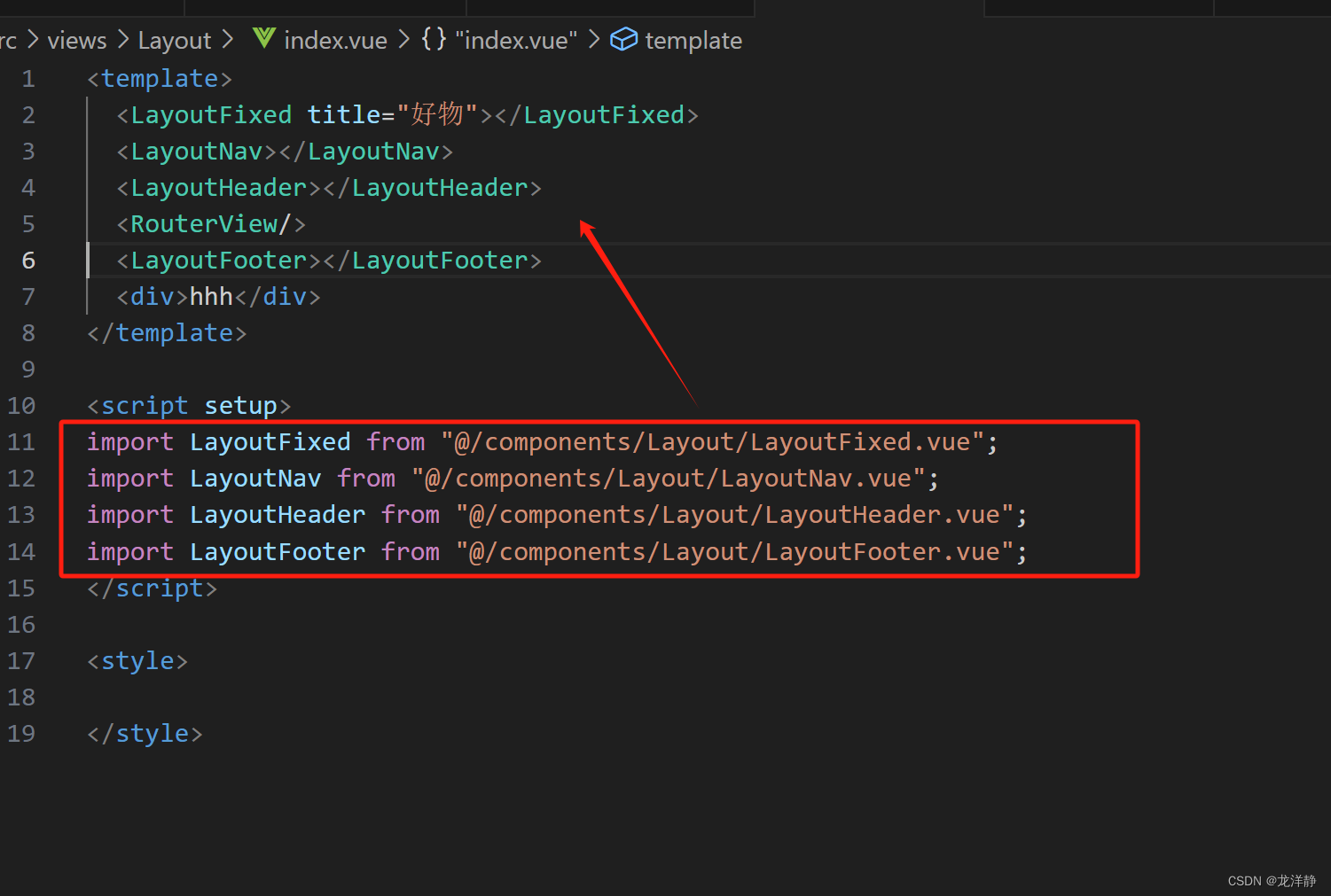
前端项目,个人笔记(二)【Vue-cli - 引入阿里矢量库图标 + 吸顶交互 + setup语法糖】
目录 1、项目中引入阿里矢量库图标 2、实现吸顶交互 3、语法糖--<script setup> 3.1、无需return 3.2、子组件接收父组件的值-props的使用 3.3、注册组件 1、项目中引入阿里矢量库图标 步骤一:进入阿里矢量库官网中:iconfont-阿里巴巴矢量…...

OpenCV 介绍使用
返回:OpenCV系列文章目录(持续更新中......) 上一篇:OpenCV4.9.0开源计算机视觉库使用简要说明 下一篇: OpenCV(开源计算机视觉库:http://opencv.org)是一个开源库,包含数百种计算机视觉算法。…...

Python 10个面试题实例
当然!以下是10个Python面试题及其示例解决方案的中题目: 1.反转字符串: string "Hello, World!" reversed_string string[::-1] print(reversed_string)2.检查字符串是否为回文: def is_palindrome(string):return string string[::-1]r…...
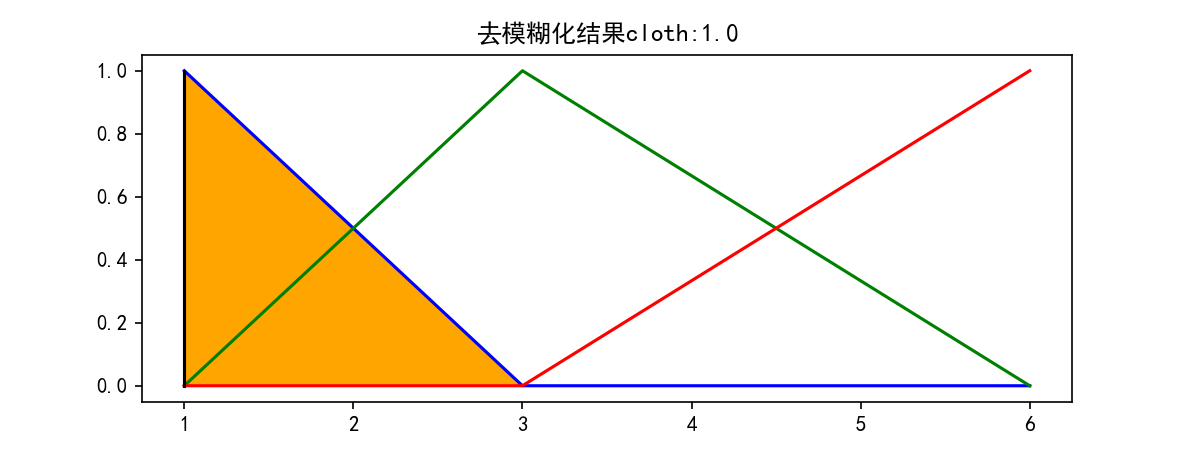
Python:熟悉简单的skfuzzy构建接近生活事件的模糊控制器”(附带详细注释说明)+ 测试结果
参考资料:https: // blog.csdn.net / shelgi / article / details / 126908418 ————通过下面这个例子,终于能理解一点模糊理论的应用了,感谢原作。 熟悉简单的skfuzzy构建接近生活事件的模糊控制器 假设下面这样的场景, 我们希望构建一套…...

opencv函数使用查找
opencv官方文档地址:https://docs.opencv.org/4.x/index.html 先选对应的版本opencv-python 以这个函数为例子 model cv2.face.LBPHFaceRecognizer.create() 点开后找face类的LBP里面就有create函数的用法...

使用 pypdf 快速切分 PDF 文件
categories: [Python] tags: Python MacOS 写在前面 最近有小伙伴问我怎么把 PDF 文档切分成两个大小相近的 PDF文档, 要是在 mac 上, 直接无脑预览就行了, 但是这样不够跨平台, 之后我也尝试过 pymupdf, 但是奈何不支持 arm 架构, 后来还是用 Python 原生的 pypdf 了. 有 AI…...

Avalonia(11.0.2)+.NET6 打包运行到银河麒麟V10桌面系统
操作系统配置 项目结构 .net版本 这次我们是在银河麒麟V10系统上打包运行Avalonia(11.0.2)+.NET6.0的程序 开始打包 准备Linux下的桌面快捷方式以及图标 调整AvaloniaApplication2.Desktop.csproj的配置项,重点看下图红色线圈出来的部分,里面涉及到了LinuxPath的设置。完整的配…...
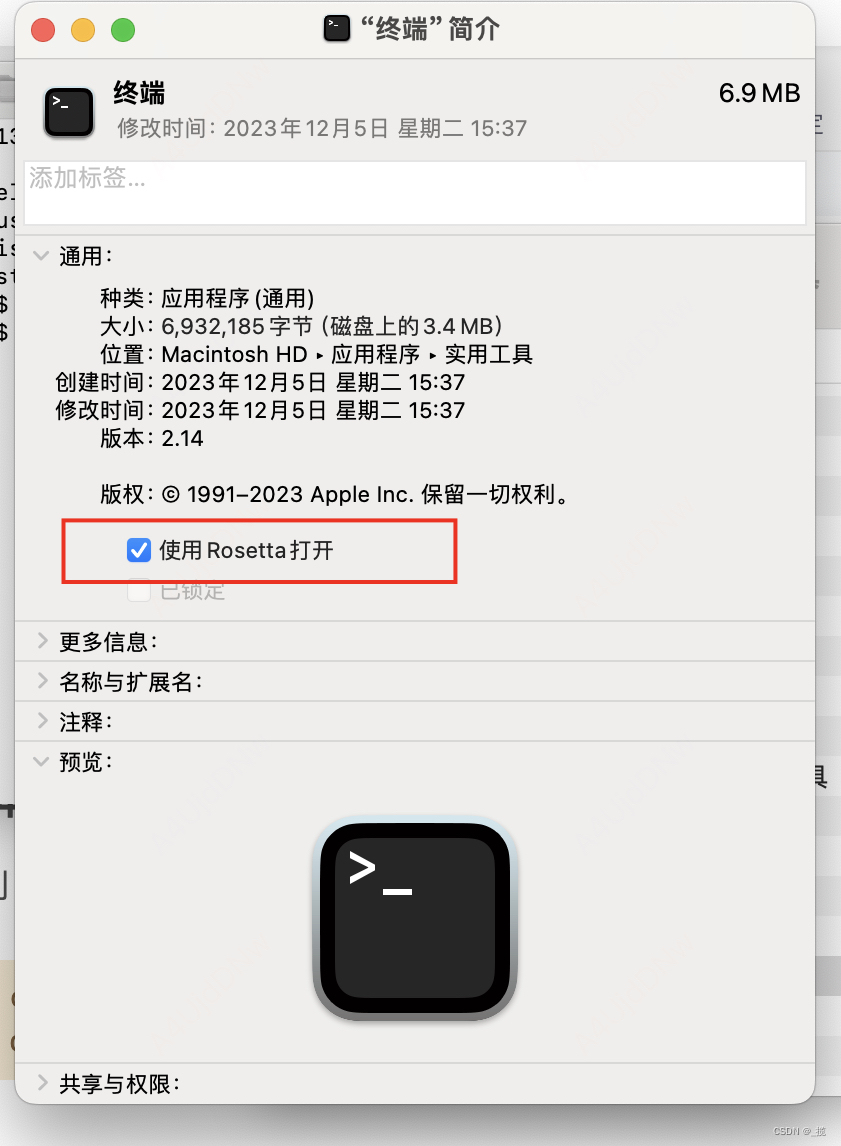
Mac nvm install failed python: not found
报错 $>./configure --prefix/Users/xxx/.nvm/versions/node/v12.22.12 < ./configure: line 3: exec: python: not found nvm: install v12.22.12 failed!解决方法 到 App 文件夹,并且打开 cd /System/Applications/Utilities/ open .记得改完 Rosetta 之…...

C语言基础知识复习(考研)
(1)C语言文件操作 1 什么是文件 文件有不同的类型,在程序设计中,主要用到两种文件: (1)程序文件。包括源程序文件(后缀为.c)、目标文件(后缀为.obj)、可执行这种文件的内容是程序代码。 (2)数据文件。文件的内容不是…...

Prometheus Grafana 配置仪表板
#grafana# 其实grafana提供了丰富的Prometheus数据源的仪表板,基本上主流的都有,通过下面官方地址可查阅 Dashboards | Grafana Labs 这里举例说明,配置node_exporter仪表板 首先,在上面的网站搜索 node 可以查到蛮多的仪表板…...
docker 哲学 - 网络桥接器、容器网络接口 、容器间的通信方式
1、解释 docker0 veth eth 2、vethXX 和 ethXX 是肯定一一对应吗 比如 eth1 对应 veth1 3、如果 A容器使用 默认创建方式 。定义他内部网络为 eth0,容器B使用 --network 连上 已创建的网络 172.89.2.1 。此时假设 B的 ip是 172.89.2.2 ,容器网络接口是 e…...
Python 将HTML转为PDF、图片、XML、XPS格式
网页内容是信息传播的主要形式之一。在Web开发中,有时候我们需要将HTML文件以不同的格式保存或分享,比如PDF、图片(如PNG或JPEG)、XML或XPS等。这些格式各有优势,适合不同的用途。在这篇文章中,我们将介绍如…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
