C语言:二叉树基础
一、树
1.1 树的概念
1.树是有n个节点组成的具有层次关系的集合,是一种非线性的结构。
2.树的第一个节点称为根,根没有前驱节点。
3.除了根节点,其余每个节点都只有一个前驱节点,有0个或多个后继节点。
4.节点的度:一个节点含有子树的个数(后继节点的个数)称为该节点的度。
5.叶子节点或终端节点:度为0的节点。
6.非终端节点或分支节点:度不为0的节点。
7.父节点或子节点:如果一个节点含有子节点(后继节点),则这个节点为子节点的父节点。
8.子节点或孩子节点:如果一个节点含有父节点(前驱节点),则这个节点为父节点的子节点。
9.兄弟节点:具有相同父节点的节点互为兄弟节点。
10.树的度:在一颗树中,所有节点中度最大的节点的度,就是这颗树的度。
11.节点的层次:从根开始位第一层,根的子节点为第二层,以此类推。
12.树的高度或深度:节点的最大层次即为树的高度。
13.堂兄弟节点: 两个节点的父节点在同一层的节点互为堂兄弟节点。
14.节点的祖先:从该节点到根经过的所有节点均为该节点的祖先。根节点是所有节点的祖先。
15.子孙:以某一个节点为根的子树中的任意节点都是该节点的子孙。
16.森林:有n(n>0)棵互不相交的树的集合称为森林。
二、二叉树
2.1二叉树的概念
1.概念:如果一颗树的所有节点的子节点都不超过2,则这颗树可以称为二叉树。
2.满二叉树:如果一个二叉树的每一层节点数都达到最大,则这个二叉树为满二叉树。
3.完全二叉树:完全二叉树与满二叉树的区别在最后一层,完全二叉树的最后一层最后一层可以不满,但从左至右的节点必须连续不能有空。满二叉树是一种特殊的完全二叉树。
4.二叉树的性质:
1. 若规定根节点的层数为i,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
2. 若规定根节点的层数为i,则深度为h的二叉树的最大结点数是2^i-1.
相关文章:

C语言:二叉树基础
一、树 1.1 树的概念 1.树是有n个节点组成的具有层次关系的集合,是一种非线性的结构。 2.树的第一个节点称为根,根没有前驱节点。 3.除了根节点,其余每个节点都只有一个前驱节点,有0个或多个后继节点。 4.节点的度&#x…...

LeetCode热题Hot100-两数之和
充分意识到Coding能力的重要性,重启算法刷题之旅。 没想到这么简单的题目都写的磕磕绊绊。 一刷只写自己的解,二刷再看有没有其他更巧妙的方法~ 题目: 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目…...
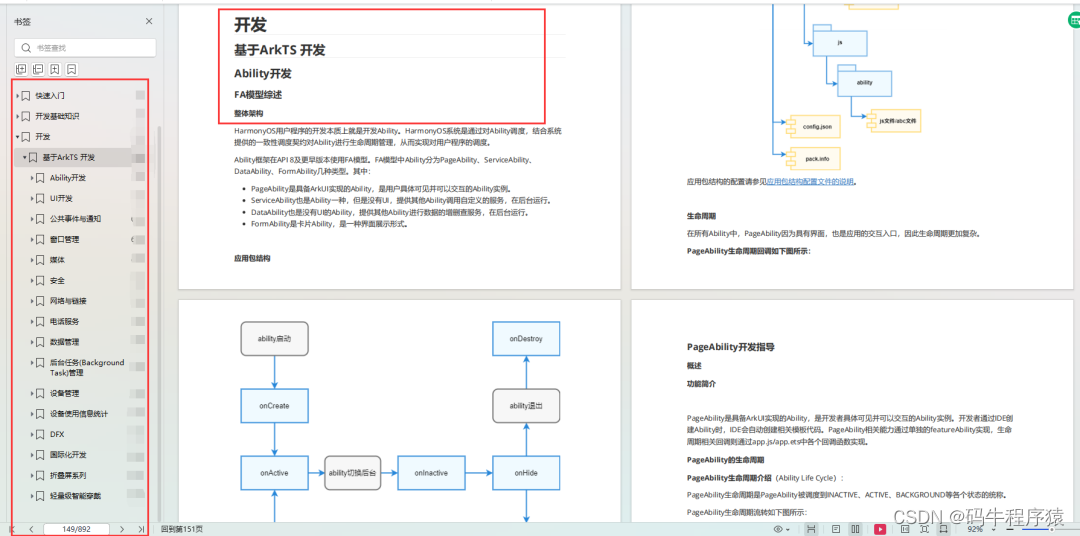
鸿蒙实战开发-如何通过拖动滑块调节应用内字体大小
介绍 本篇Codelab将介绍如何使用基础组件Slider,通过拖动滑块调节应用内字体大小。要求完成以下功能: 实现两个页面的UX:主页面和字体大小调节页面。拖动滑块改变字体大小系数,列表页和调节页面字体大小同步变化。往右拖动滑块字…...

matlab实现神经网络检测手写数字
一、要求 1.计算sigmoid函数的梯度; 2.随机初始化网络权重; 3.编写网络的代价函数。 二、算法介绍 神经网络结构: 不正则化的神经网络的代价函数: 正则化: S型函数求导: 反向传播算法&…...

增强现实与虚拟现实中的大模型应用:沉浸式体验的创新
增强现实与虚拟现实中的大模型应用:沉浸式体验的创新 1. 背景介绍 随着技术的进步,增强现实(AR)和虚拟现实(VR)正在成为越来越受欢迎的沉浸式体验方式。大模型,如神经网络和深度学习模型&…...
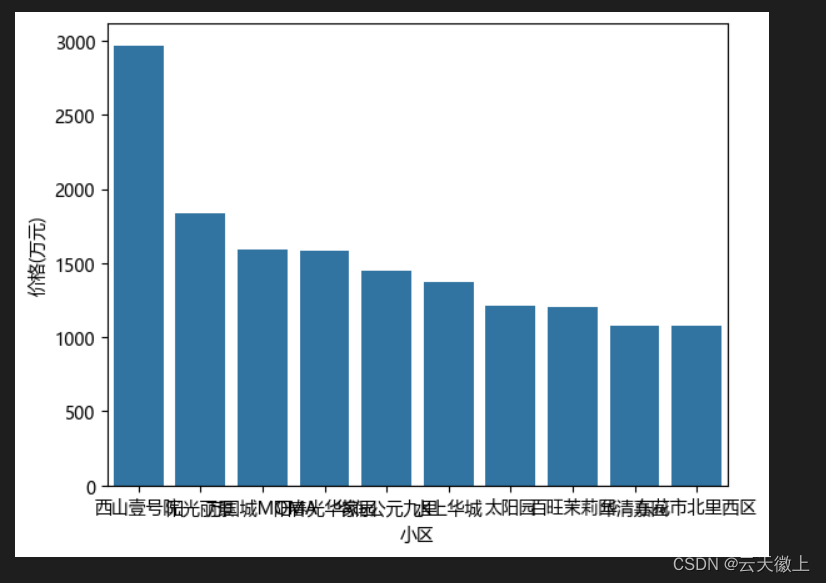
【数据分析案列】--- 北京某平台二手房可视化数据分析
一、引言 本案列基于北京某平台的二手房数据,通过数据可视化的方式对二手房市场进行分析。通过对获取的数据进行清冼(至关重要),对房屋价格、面积、有无电梯等因素的可视化展示,我们可以深入了解北京二手房市场的特点…...

【Golang星辰图】创造美丽图表,洞察数据:解析Go语言中的数据可视化和数据分析库
解锁数据的力量:深入研究Go语言中的数据可视化和数据分析库 前言 本文将介绍Go语言中几个优秀的数据可视化和数据分析库,以帮助开发者更好地处理和分析数据。这些库提供了丰富的功能和工具,可用于创建漂亮的可视化图表、进行数值计算和数据…...

阿里云原生:如何熟悉一个系统
原文地址:https://mp.weixin.qq.com/s/J8eK-qRMkmHEQZ_dVts9aQ?poc_tokenHMA-_mWjfcDmGVW6hXX1xEDDvuJPE3pL9-8uSlyY 导读:本文总结了熟悉系统主要分三部分:业务学习、技术学习、实战。每部分会梳理一些在学习过程中需要解答的问题,这些问题…...
)
Scala第十一章节(正则表达式和异常处理)
4. 正则表达式 4.1 概述 所谓的正则表达式指的是正确的,符合特定规则的式子, 它是一门独立的语言, 并且能被兼容到绝大多数的编程语言中。在scala中, 可以很方便地使用正则表达式来匹配数据。具体如下: Scala中提供了Regex类来定义正则表达式.要构造一个Regex对象࿰…...

Flutter运行MacOs网络请求报错Unhandled Exception: DioException [connection error]:...
报错信息 [ERROR:flutter/runtime/dart_vm_initializer.cc(41)] Unhandled Exception: DioException [connection error]: The connection errored: Connection failed This indicates an error which most likely cannot be solved by the library. Error: SocketException: …...
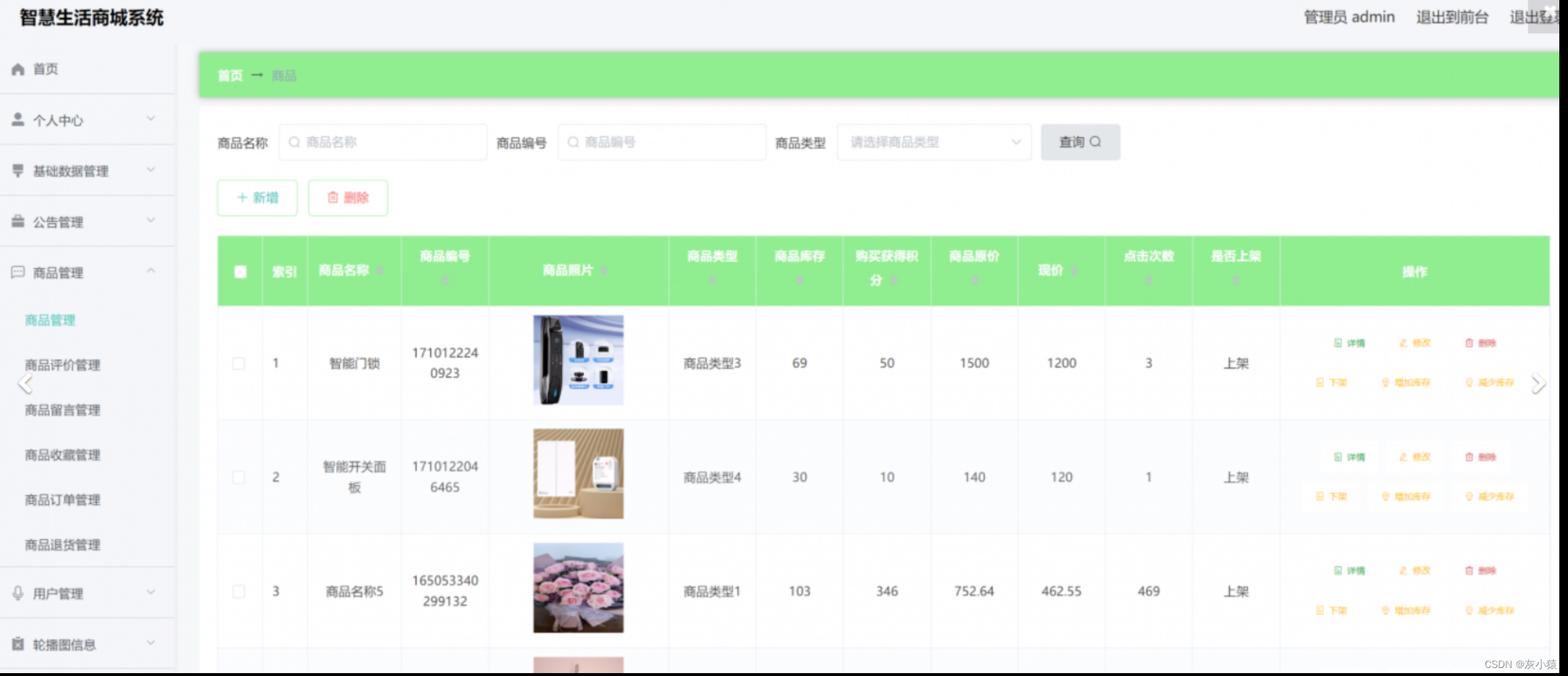
基于SpringBoot+MyBatis框架的智慧生活商城系统的设计与实现(源码+LW+部署+讲解)
目录 前言 需求分析 可行性分析 技术实现 后端框架:Spring Boot 持久层框架:MyBatis 前端框架:Vue.js 数据库:MySQL 功能介绍 前台功能拓展 商品详情单管理 个人中心 秒杀活动 推荐系统 评论与评分系统 后台功能拓…...
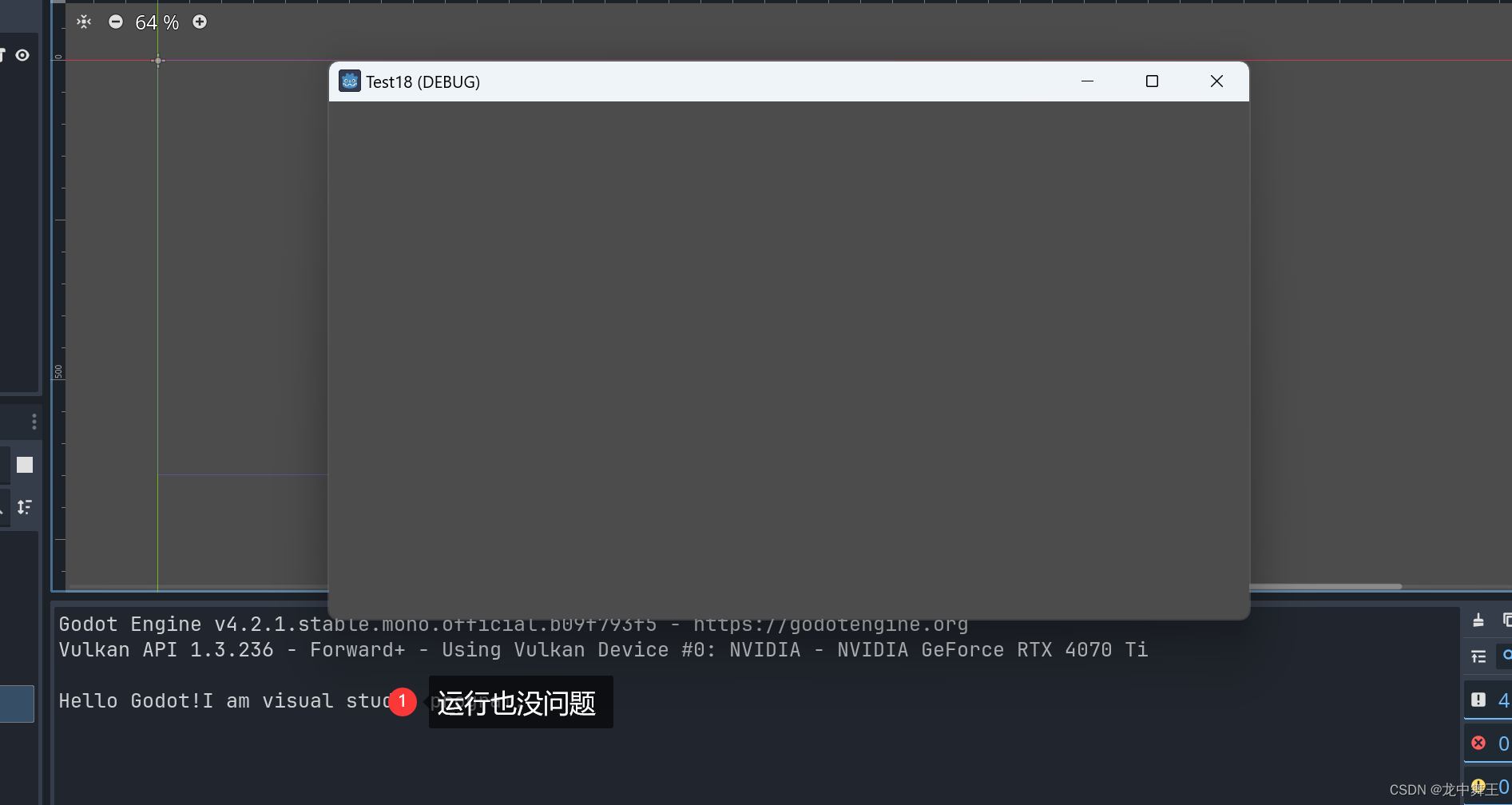
Godot 学习笔记(5):彻底的项目工程化,解决GodotProjectDir is null
文章目录 前言GodotProjectDir is null解决方法解决警告问题根本解决代码问题测试引用其实其它库的输出路径无所谓。 总结 前言 Godot 项目工程化上有一朵乌云,我看Godot的Visual Studio 项目的时候,发现如果是手动新建项目导入Godot包,会导…...

Openharmony
OpenHarmony 是一个开源的、多设备分布式操作系统,由开放原子开源基金会(OpenAtom Foundation)孵化及运营。它旨在提供跨多种设备的统一开发体验,支持一次开发,多端部署。OpenHarmony 的系统架构遵循分层设计原则&…...

24计算机考研调剂 | 华南师范大学
华南师范大学接收调剂研究生 考研调剂招生信息 学校:华南师范大学 专业:- 年级:2024 招生人数:- 招生状态:正在招生中 联系方式:********* (为保护个人隐私,联系方式仅限APP查看) 补充内容 课题组主要研究生物拉曼光谱技术、基于荧光的微生物快检技术、显微成像设备与相…...
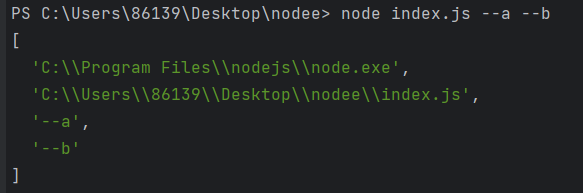
【Node.js】全局变量和全局 API
node 环境中没有 dom 和 bom ,此外 es 基本上都是可以正常使用的。 如果一定要使用 dom 和bom,可以借助第三方库 jsdom 帮助我们实现操作。npm i jsdom 实例: const fs require(node:fs) const {JSDOM} require(jsdom)const dom new JS…...

Install Docker
Docker Desktop 直接安装 Docker Desktop Docker Desktop includes the Docker daemon (dockerd), the Docker client (docker), Docker Compose, Docker Content Trust, Kubernetes, and Credential Helper. Linux下安装Docker CE 参考官方文档 参见阿里云的文档 # step 1…...

Orbit 使用指南 10|在机器人上安装传感器 | Isaac Sim | Omniverse
如是我闻: 资产类(asset classes)允许我们创建和模拟机器人,而传感器 (sensors) 则帮助我们获取关于环境的信息,获取不同的本体感知和外界感知信息。例如,摄像头传感器可用于获取环境的视觉信息,…...

GPT系列模型的特点
GPT系列模型(包括GPT-1、GPT-2和GPT-3)都基于自回归机制的Transformer架构。在设计上,这些模型的核心思想是利用Transformer架构来捕捉整个序列的上下文信息,通过其独特的自回归机制逐步地整合整个序列的完整语义。GPT系列模型的设…...

Oracle Data Guard常用命令
--查询数据库角色和保护模式 select database_role,switchover_status from v$database; --切换备库为主库(切换后,主库为mount状态) --TO PRIMARY alter database commit to switchover to primary; --SESSIONS ACTIVE alter database comm…...
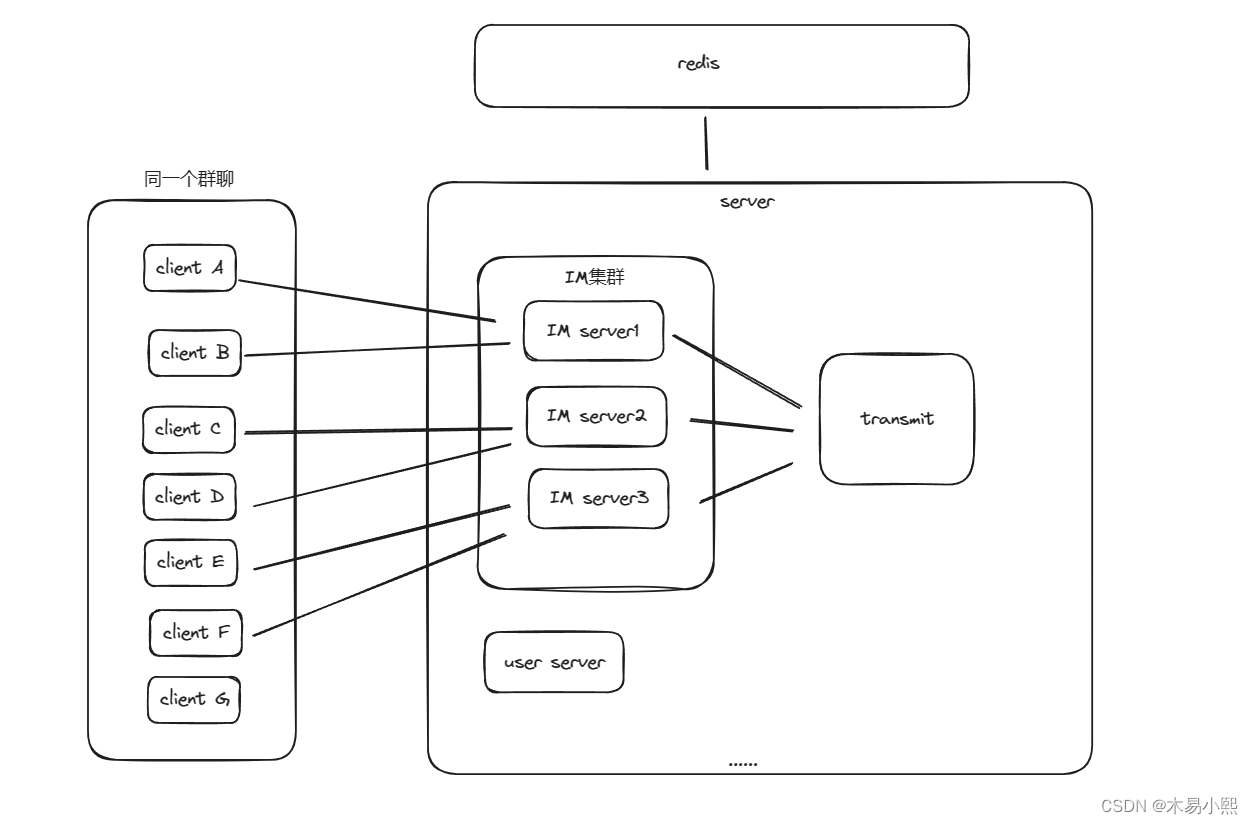
IM系统设计之websocket消息转发
Websocket消息转发 项目地址:gitgithub.com:muyixiaoxi/Link.git 上周面试被面试官问到:“在分布式IM系统中,如何实现多个websocket集群之间的通信”。 我在思考了良久后回答:“不会”。 随着我的回答,我和面试官的…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
