【算法每日一练]-图论(保姆级教程篇16 树的重心 树的直径)#树的直径 #会议 #医院设置
目录
树的直径
题目:树的直径 (两种解法)
做法一:
做法二:
树的重心:
题目: 会议
思路:
题目:医院设置
思路:
树的直径
定义:树中距离最远的两个点之间的距离被称为树的直径。
一共有两种做法,先记结论,再给证明!
(1)任取一点作为起点x,找到距离该点最远的一个点y;
(2)再找到距离y最远的一点z,那么y、z之间的路径就是一条直径。
做法二:
(1)距离直径上的一个点最远的点和次远的点一定是直径的两个顶点,所以我们只要能找到距离每一个点的最远距离和次远距离就能找到树的直径了。
做法一证明:核心是证明y一定是直径的一个端点。
使用反证法证明,假设xy是直径(x,y为直径上点),uv为非直径(u,v为非直径上点)。存在如下两种情况。
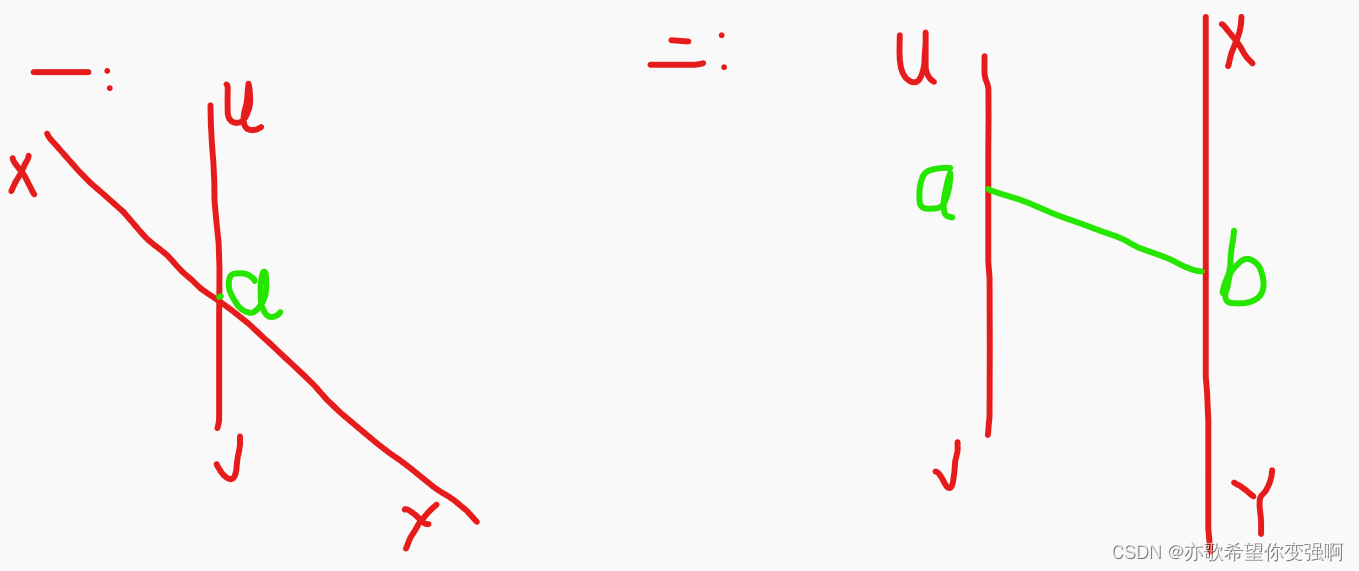
-
第一种情况是两者相交,故意假设v是距离u最远的点,有以下推论:
ua+av>ua+ay => av>ay => av+ax>ay+ax=xy
假设不成立,因v可以代表任意一个不是直径上的点,故距离u最远的点一定是直径上的点!
-
第二种情况是两者不相交,故意假设v是距离u最远的点,有以下推论:
ua+av>ua+ab+by => av > ab+by => av+ab+bx>ab+by+ab+bx=2*ab+xy
假设不成立,因v可以代表任意一个不是直径上的点,故距离u最远的点一定是直径上的点!
做法二证明:
前半句话不用……就不证明了吧,后半句“ 只要能找到距离每一个点的最远距离和次远距离就能找到树的直径了。” 意思就是把任意两点间的最长距离在某一点处砍成两半,当然有距离此点的最长距离和次长距离就是两头顶点间的最长距离,那么对所有点统计一下自然就找到直径长度了。
题目:树的直径 (两种解法)
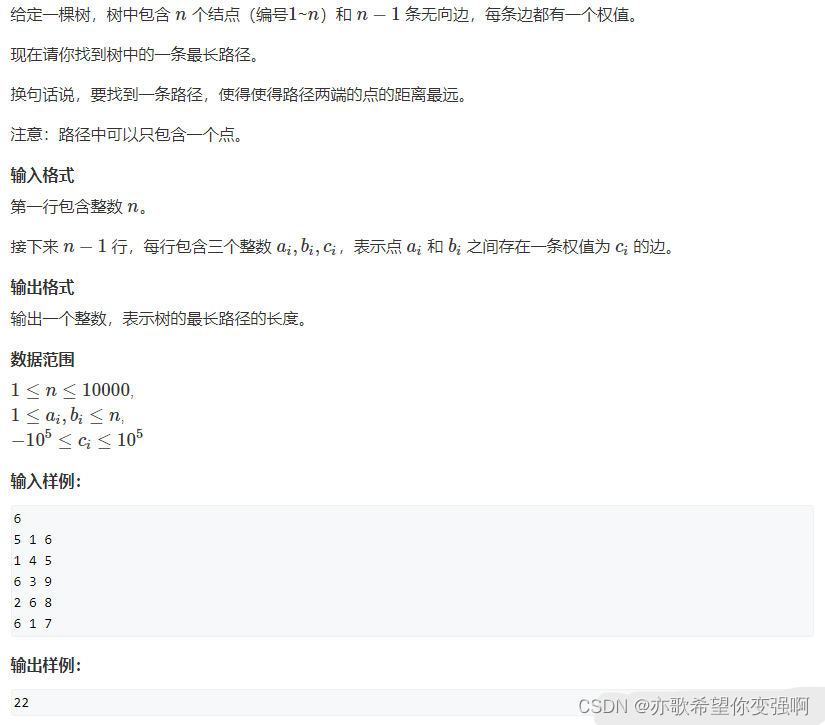
spfa,dijkstra多用于跑有环的图,DAG图求最长距离直接dfs_dp就行!
做法一:
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int tot,n,d[N],head[N];//d[i]表示到i点的距离
struct node{int to,w,nxt;}e[N*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}void dfs(int u,int fa){for(int i=head[u];i;i=e[i].nxt){int v=e[i].to,w=e[i].w;if(v==fa)continue;d[v]=d[u]+w;//先更新再递归,因为d表示到u点的距离dfs(v,u);}
}
int main(){cin>>n;int u,v,w;for(int i=1;i<=n-1;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}dfs(1,0);//从任意点找最远距离的点int ans=-1;for(int i=1;i<=n;i++)if(d[i]>ans)ans=d[i],v=i;memset(d,0,sizeof(d));dfs(v,0);//此点必定在直径上,再跑一遍就完了for(int i=1;i<=n;i++)if(d[i]>ans)ans=d[i];cout<<ans;
}
做法二:
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int ans=-1,tot,n,head[N];//d[i]表示到i点的距离
struct node{int to,w,nxt;}e[N*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}int dfs(int u,int fa){int d1=0,d2=0;//d1是最长距离,d2是次长距离for(int i=head[u];i;i=e[i].nxt){int v=e[i].to,w=e[i].w;if(v==fa)continue;int d3=dfs(v,u)+w;//先更新距离if(d3>=d1) d2=d1,d1=d3;//如果是更长距离,最长和次长都更新else if(d3>d2)d2=d3;//如果仅比次长距离大,就仅更新次长距离}ans=max(ans,d1+d2);//最长距离加次长距离就是总长度return d1;//返回最长距离
}
int main(){cin>>n;int u,v,w;for(int i=1;i<=n-1;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}dfs(1,0);//从任意点开始cout<<ans;}
树的重心:
题目: 会议


思路:
首先,阅读题目可以看出来,这道题目实际上就是求树的重心。
树的重心:
定义:找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,达到的效果是生成的多棵树尽可能平衡。
举个例子:
我们不妨设置d[i]表示以此点为根的所有点总距离和,cnt[i]表示以此为根的节点数

我们首先知道d[1]=16,cnt[1]=10我们来看d[2]应该怎么求,我们发现相对于d[1]来说,如果设2为最佳点,2,5,6其距离-1,剩下的1,4,3,7,8,9,10到其距离+1。
故:d[2]=d[1] - 3 + 7 =20
其中3是子根2对应的节点数cnt[2],7是1为子根对应的节点数cnt[1]-cnt[2]
得:d[i]=d[fa]-cnt[i]+(cnt[1]-cnt[i])
那么只需要先dfs求出来d[1]和每个点的cnt[i]。然后就可以进行dp最终求出所有点的d[i]。
#include <bits/stdc++.h>
using namespace std;
const int N=50005;
int minn=0x3f3f3f3f,ans,n,d[N],cnt[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){//一定别走fa回去cnt[u]++;//先加上自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);//先求孩子的cnt,之后求自己cntcnt[u]+=cnt[v];}d[1]+=len;//最后求d[1]
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]-2*cnt[v]+cnt[1];dp(v,u);//这里对自己进行转移更新,再对孩子的更新}
}
int main(){cin>>n;int a,b;for(int i=1;i<n;i++){cin>>a>>b;ve[a].push_back(b);ve[b].push_back(a);}dfs(1,0,0);dp(1,0);for(int i=1;i<=n;i++){if(d[i]<minn)minn=d[i],ans=i;}cout<<ans<<" "<<minn;
}
上面我打注释的地方一定要理解
题目:医院设置

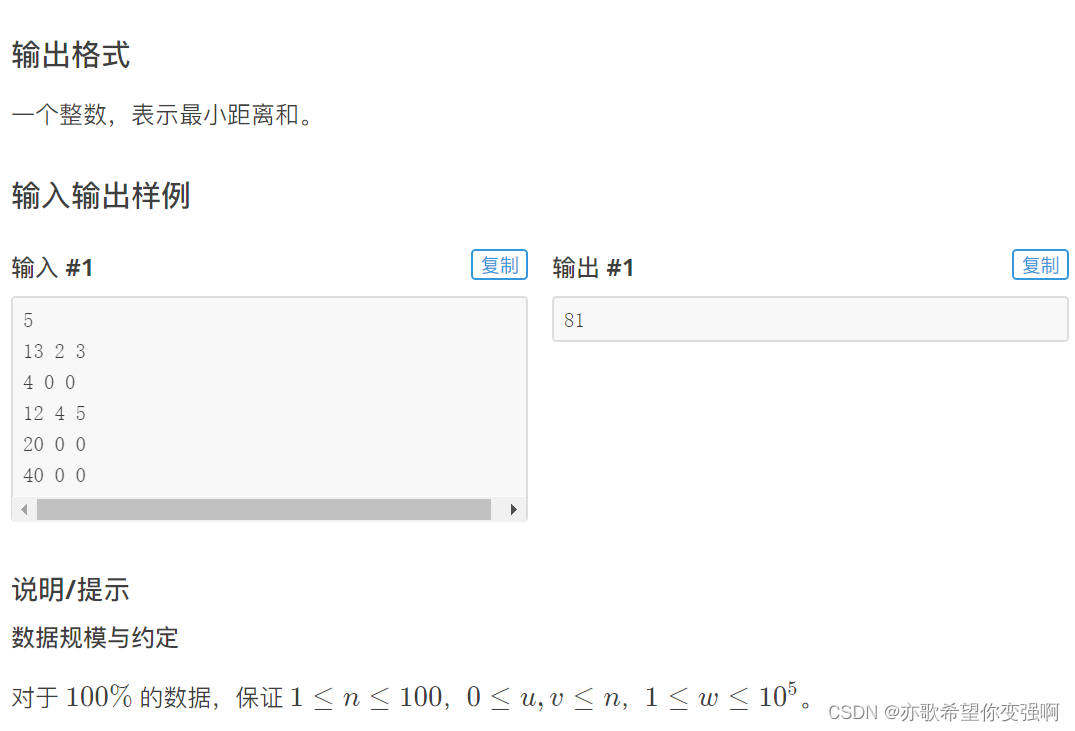
思路:
还是一道求树的重心题。不过是每个点都有一个权值。那么把权值当成“另一个世界的节点数”就好了。然后不断求cnt,之后dp就行。
#include <bits/stdc++.h>
using namespace std;
const int N=500;
int ans=0x3f3f3f3f,n,d[N],cnt[N],w[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){cnt[u]=w[u];//这里还是先加自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);cnt[u]+=cnt[v];}d[1]+=len*w[u];//更新d[1]也要变一下
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]+cnt[1]-cnt[v]*2;dp(v,u);}ans=min(ans,d[u]);
}
int main(){cin>>n;int c,a,b;for(int i=1;i<=n;i++){cin>>c>>a>>b;w[i]=c;//注意输入方式if(a)ve[i].push_back(a),ve[a].push_back(i);if(b)ve[i].push_back(b),ve[b].push_back(i);}dfs(1,0,0);dp(1,0);cout<<ans;
}
相关文章:

【算法每日一练]-图论(保姆级教程篇16 树的重心 树的直径)#树的直径 #会议 #医院设置
目录 树的直径 题目:树的直径 (两种解法) 做法一: 做法二: 树的重心: 题目: 会议 思路: 题目:医院设置 思路: 树的直径 定义:树中距离最…...
Qt播放音乐代码示例
主界面 点击play按钮播放或暂停音乐,拖动进度条,音乐对应播放。 QWidget window;QPushButton* playButton new QPushButton("Play");// Qt 播放音乐// 创建 QMediaPlayer 对象QMediaPlayer* player new QMediaPlayer;// 指定音频文件的路径…...

多线程应用中的性能优化:创建合适的线程数
多线程应用中的性能优化:创建合适的线程数 在多线程应用中,为了降低延迟和提高吞吐量,我们可以采取两种主要策略:优化算法或者充分利用硬件性能。要发挥硬件的极致性能,就需要使用多线程来提高CPU或I/O的利用率。 由于…...
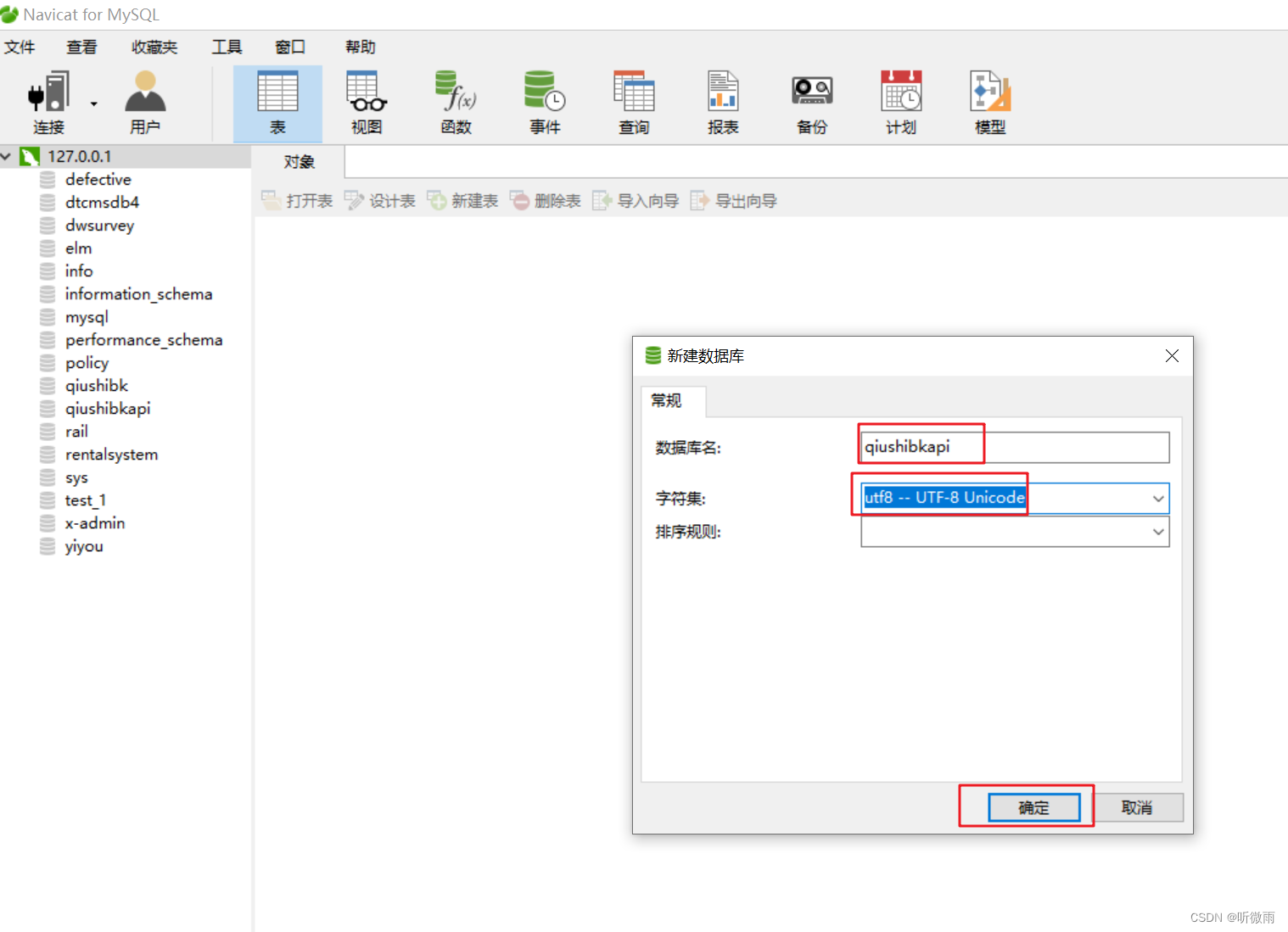
本地运行环境工具UPUPWANK(win)和Navicat数据库管理工具
UPUPWANK安装地址:https://www.upupw.net 1.进入UPUPWANK后点击一键开启 2.新增项目 这里请千万注意80端口,如果80端口被占用了,请记住去任务管理器关闭占用80端口的进程。不然就不会成功显示。(笔者含泪警告,一晚上的…...

LeetCode 每日一题 2024/3/18-2024/3/24
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 3/18 303. 区域和检索 - 数组不可变3/19 1793. 好子数组的最大分数3/20 1969. 数组元素的最小非零乘积3/21 2671. 频率跟踪器3/22 2617. 网格图中最少访问的格子数3/23 254…...

Unity 鼠标拖拽3D物体跟随移动的方法
之前我们研究过UI拖拽跟随鼠标移动的方法:https://blog.csdn.net/mr_five55/article/details/135562325 但是该方法不适合3D场景。 假如我们要通过鼠标拖拽3D物体移动,那么可以使用以下控制方法: using System.Collections; using System.…...

数据分析-Pandas分类数据的类别排序和顺序
数据分析-Pandas类别的排序和顺序 数据分析和处理中,难免会遇到各种数据,那么数据呈现怎样的规律呢?不管金融数据,风控数据,营销数据等等,莫不如此。如何通过图示展示数据的规律? 数据表&…...

利用 Claude 3 on Amazon Bedrock 和 Streamlit 的“终极组合”,开发智能对话体验
概述 通过本文,您将学会如何利用 Streamlit 框架快速搭建前端交互界面。该界面将集成图像上传功能,让用户可以方便地提交待处理图片。在后端,我们将借助 Amazon Bedrock 的 Message API,调用 Claude 3 家族中的 Sonnet 模型对图像…...

Golang基础 Label标签与goto跳转
使用方法 Label 和goto是必须的 Label可以声明再函数体的任何地方 Label的作用范围是在函数体中 Label在嵌套函数(闭包)是不可用的. 不管是在闭包里调用闭包外的Label, 还是在闭包外调用闭包里的Label 变量的声明必须在goto之前 示例 package mainimport "fmt"…...

二进制王国(蓝桥杯备赛)【sort/cmp的灵活应用】
二进制王国 题目链接 https://www.lanqiao.cn/problems/17035/learning/?contest_id177 题目描述 思路 这里就要灵活理解字典序排列,虽然string内置可以直接比较字符串字典序,但是在拼接时比较特殊,比如 11的字典序小于110,但…...

活用C语言之宏定义应用大全
零、C语言宏定义知多少 C语言的编程过程中经常会用到宏定义,然而如果你只是使用宏定义做一些常量的定义,那么你不是OUT了就是C语言小白。 那么我们在编程过程中,宏定义都有哪些作用呢? 常量定义 可以作为功能代码的开关 防止头文件被重复…...

【源码】I.MX6ULL移植OpenCV
编译完成的源码: git clone https://gitee.com/wangyoujie11/atkboard_-linux_-driver.git 1.下载源码放在自己的opecv源码目录下 2.QTOpenCV工程代码放置的位置 3.更改.pro工程文件的opencv地址 4.使用命令行编译 前提是自己环境中已经配置好arm-qt的交叉编译…...
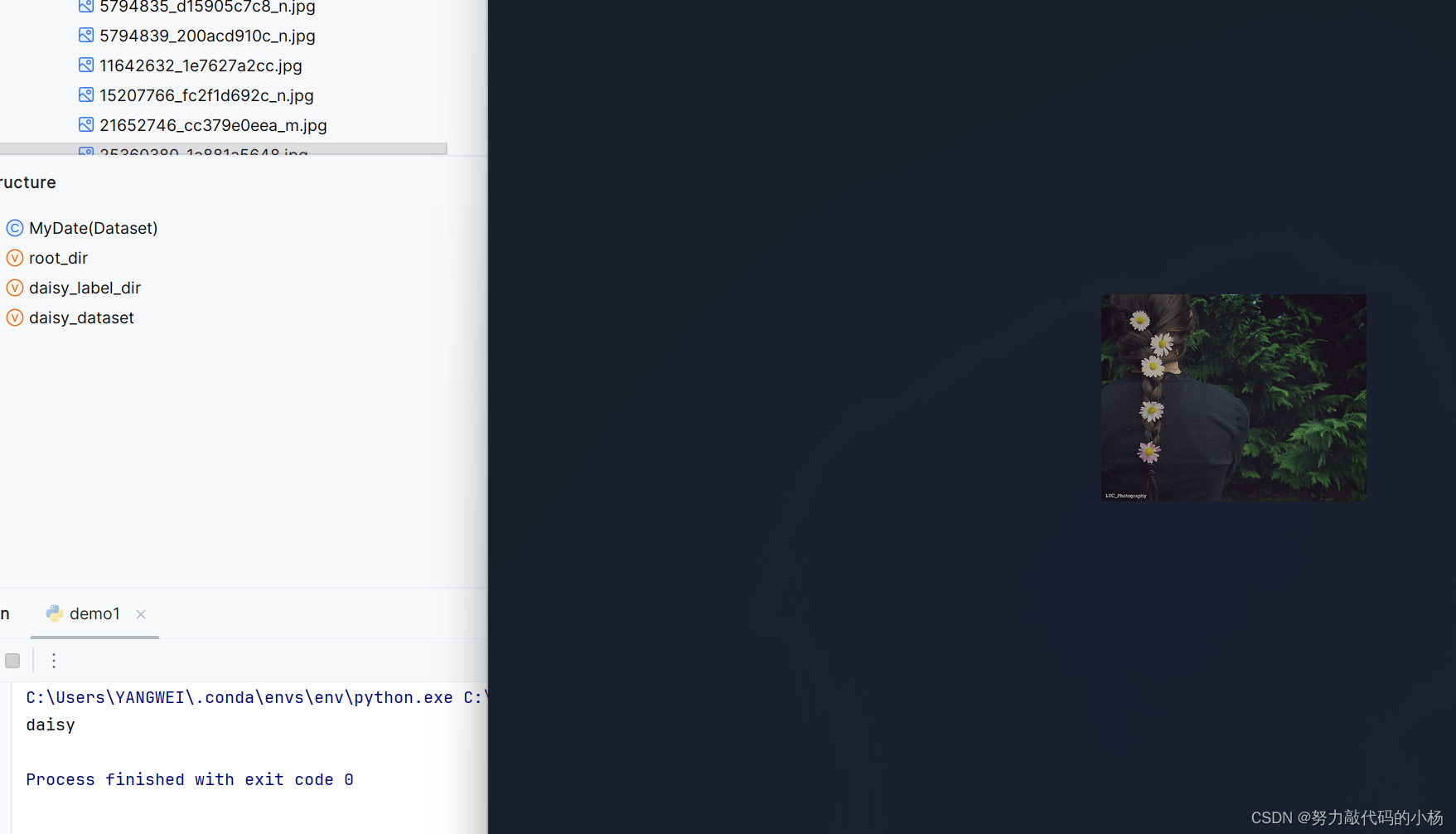
pytorch深度学习——dataset(附数据集下载)
在学习深度学习的时候,我们需要考虑如何去处理数据去训练我们的模型,pytorch为我们提供了Dataset和DataLoader两个类来对数据进行处理,前者作用是提供了一种方式来获取数据及其label,后者的作用是为网络提供不同的数据形式。本文主…...

springboot+vue考试管理系统
基于springboot和vue的考试管理系统 001 springboot vue前后端分离项目 本文设计了一个基于Springbootvue的前后端分离的在线考试管理系统,采用M(model)V(view)C(controller)三层体系结构&…...
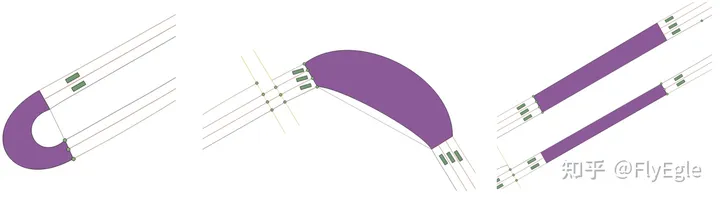
自动驾驶建图--道路边缘生成方案探讨
自动驾驶建图–道路边缘生成方案探讨 一、背景 对于自动驾驶来说,建图是必不可少的,目前主流厂商技术都在从HD到"无图"进行过渡筹备中,不过想要最终实现真正的"无图"还是有很长的一段路要走。 对于建图来说,…...
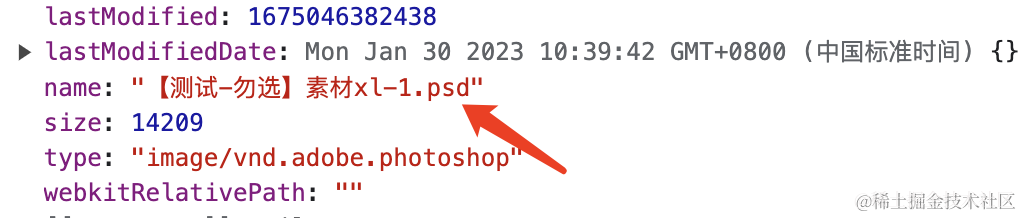
图片编辑器中实现文件上传的三种方式和二进制流及文件头校验文件类型
背景 最近在 vue-design-editor 开源项目中实现 psd 等多种文件格式上传解析成模板过程中, 发现搞定设计文件上传没有使用 input 实现文件上传, 所以我研究了一下相关技术, 总结了以下三种文件上传方法 input 文件选择window.showOpenFilePicker 和 window.showDirectoryPicke…...

深度学习,CRNN+CTC和Attention OCR你更青睐哪一种?
深度学习在OCR领域的应用已经取得了瞩目的成果,而选择合适的算法对于提升OCR的识别准确率至关重要。在众多算法中,CRNN和Attention OCR犹如两颗璀璨的明珠,备受瞩目。 CRNN,这位结合了卷积神经网络(CNN)和…...

飞桨AI应用@riscv OpenKylin
在riscv编译安装飞桨PaddlePaddle参见: 算能RISC-V通用云编译飞桨paddlepaddleopenKylin留档_在riscv下进行paddlelite源码编译-CSDN博客 安装好飞桨,就可以用飞桨进行推理了。刚开始计划用ONNX推理,但是在算能云没有装上,所以最…...

在MongoDB建模1对N关系的基本方法
“我在 SQL 和规范化数据库方面拥有丰富的经验,但我只是 MongoDB 的初学者。如何建立一对 N 关系模型?” 这是我从参加 MongoDB 分享日活动的用户那里得到的最常见问题之一。 我对这个问题没有简短的答案,因为方法不只有一种,还有…...

C++基础之运算符重载(十一)
首先为什么要对运算符进行重载?因为C内置的运算符只能作用于一些基本数据类型,而对类和结构体这种自定义数据类型是不管用的。所以这时我们需要对运算符进行重新定义满足一定的运算规则。 运算符重载的三种形式 1.以普通的函数进行重载 #include <…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
