图论基础|深度优先dfs、广度优先bfs
dfs 与 bfs 区别
提到深度优先搜索(dfs),就不得不说和广度优先搜索(bfs)有什么区别
先来了解dfs的过程,很多录友可能对dfs(深度优先搜索),bfs(广度优先搜索)分不清。
先给大家说一下两者大概的区别:
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
深度优先dfs
深度优先关键就两点:
- 搜索方向,是认准一个方向搜,直到碰壁之后再换方向
- 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。
其实深搜和回溯是非常类似的,深搜三部曲如下:
1.确认递归函数,参数
void dfs(参数)
通常我们递归的时候,我们递归搜索需要了解哪些参数,其实也可以在写递归函数的时候,发现需要什么参数,再去补充就可以。
一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。
vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图,目前搜索的节点) 2.确认 终止条件
终止条件很重要,很多同学写dfs的时候,之所以容易死循环,栈溢出等等这些问题,都是因为终止条件没有想清楚。
if (终止条件) {存放结果;return;
}
终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。
3.处理目前搜索节点出发的路径
一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点。
for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果
}797.所有可能的路径
力扣题目链接(opens new window)
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
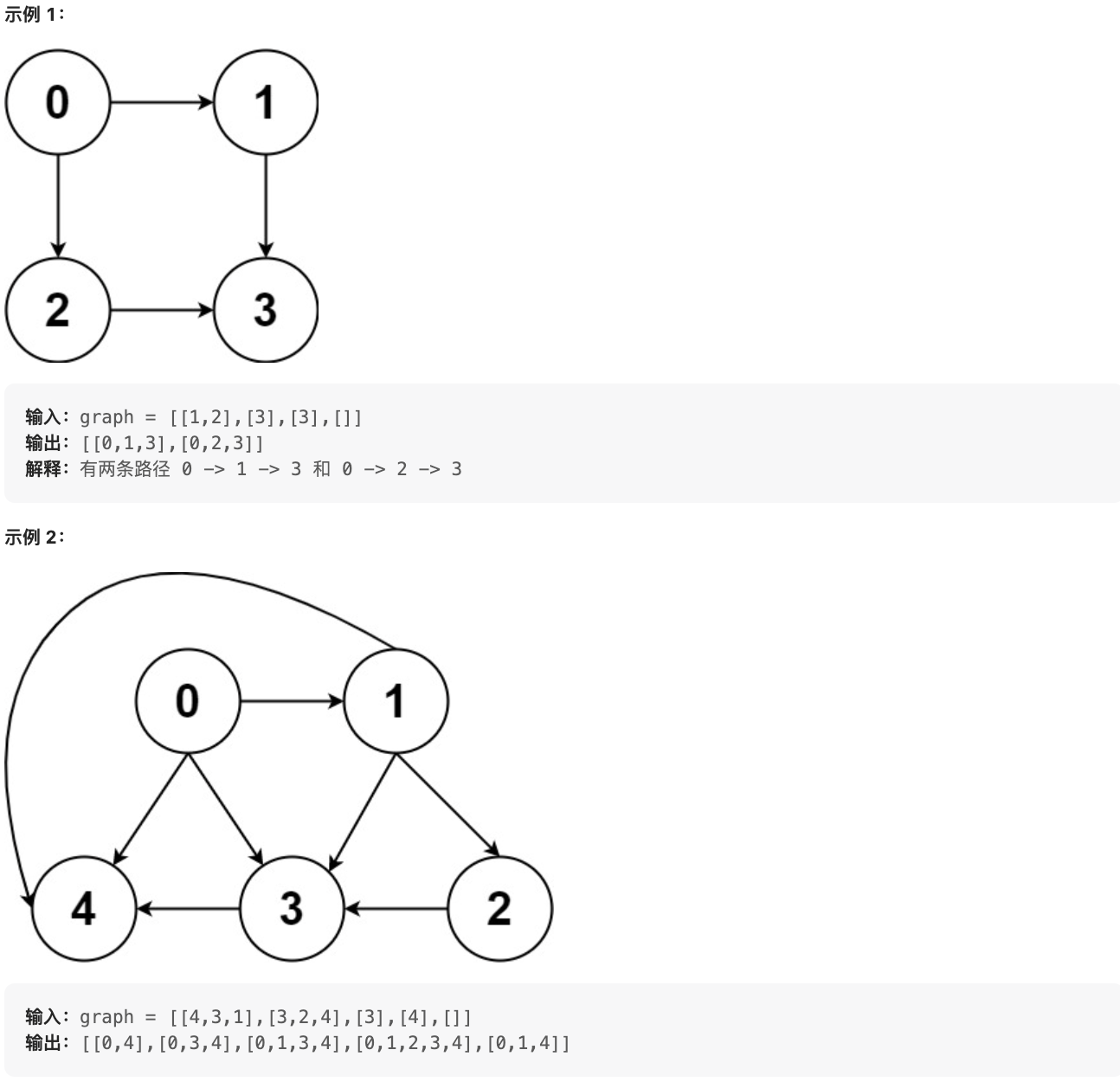
提示:
- n == graph.length
- 2 <= n <= 15
- 0 <= graph[i][j] < n
- graph[i][j] != i(即不存在自环)
- graph[i] 中的所有元素 互不相同
- 保证输入为 有向无环图(DAG)
思路:深度优先基础题目
class Solution {
public:vector<vector<int>>result;vector<int>path;void dfs(vector<vector<int>>& graph, int x){if(x==graph.size()-1){//搜索到终点,停止搜索并把可行路径加入结果数组result.push_back(path);return;}for(int i=0; i<graph[x].size(); i++){//遍历节点所能访问的所有其他节点path.push_back(graph[x][i]);dfs(graph, graph[x][i]);//递归遍历path.pop_back();//回溯}}vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {result.clear();path.clear();path.push_back(0);//从0节点出发dfs(graph,0);//从节点0开始搜索return result;}
};广度优先搜索理论基础
广度优先类似于二叉树的层序遍历
广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
上面我们提过,BFS是一圈一圈的搜索过程,但具体是怎么一圈一圈来搜呢。
我们用一个方格地图,假如每次搜索的方向为 上下左右(不包含斜上方),那么给出一个start起始位置,那么BFS就是从四个方向走出第一步。
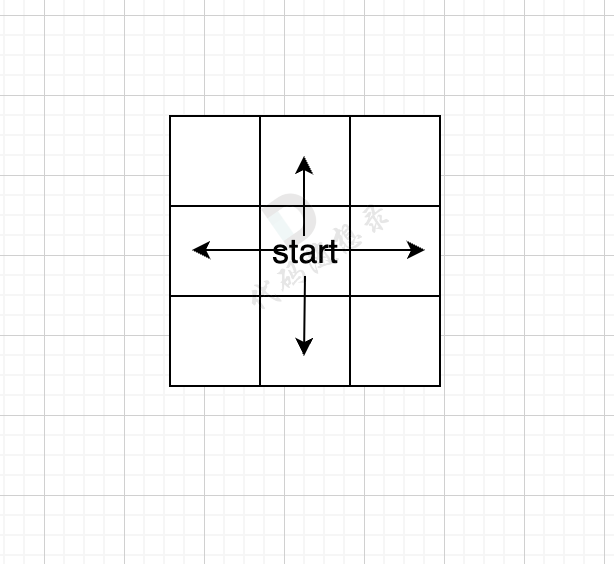
如果加上一个end终止位置,那么使用BFS的搜索过程如图所示:
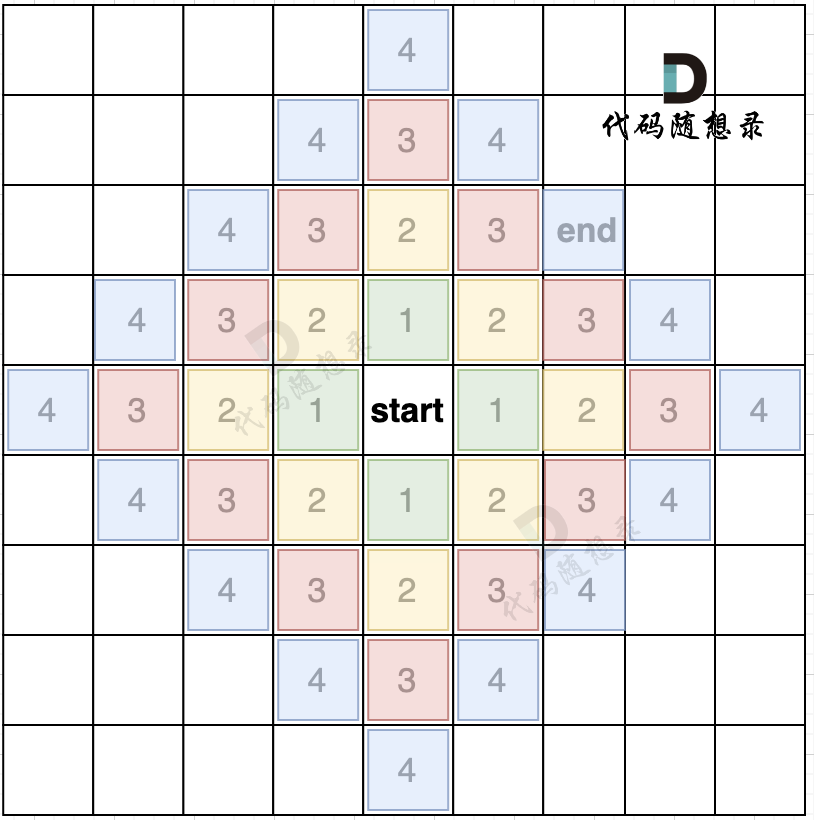
我们从图中可以看出,从start起点开始,是一圈一圈,向外搜索,方格编号1为第一步遍历的节点,方格编号2为第二步遍历的节点,第四步的时候我们找到终止点end。
正是因为BFS一圈一圈的遍历方式,所以一旦遇到终止点,那么一定是一条最短路径。
大家应该好奇,这一圈一圈的搜索过程是怎么做到的,是放在什么容器里,才能这样去遍历。
很多网上的资料都是直接说用队列来实现。
其实,我们仅仅需要一个容器,能保存我们要遍历过的元素就可以,那么用队列,还是用栈,甚至用数组,都是可以的。
用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。
因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。
因为栈是先进后出,加入元素和弹出元素的顺序改变了。
那么广搜需要注意 转圈搜索的顺序吗? 不需要!
所以用队列,还是用栈都是可以的,但大家都习惯用队列了,所以下面的讲解用我也用队列来讲,只不过要给大家说清楚,并不是非要用队列,用栈也可以。
广搜代码模板,该模板针对的就是,上面的四方格的地图: (详细注释)
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图,也就是一个二维数组
// visited标记访问过的节点,不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定义队列que.push({x, y}); // 起始节点加入队列visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点while(!que.empty()) { // 开始遍历队列里的元素pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素int curx = cur.first;int cury = cur.second; // 当前节点坐标for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历int nextx = curx + dir[i][0];int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过if (!visited[nextx][nexty]) { // 如果节点没被访问过que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问}}}}200. 岛屿数量
题目链接(opens new window)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。

提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 300
- grid[i][j] 的值为 '0' 或 '1‘
广度优先版本:
class Solution {
public:int dir[4][2]={0,1,1,0,-1,0,0,-1};//定义四个方向void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){queue<pair<int,int>> que;que.push({x,y});while(!que.empty()){pair<int, int> cur=que.front(); que.pop();//出队,访问int curx=cur.first;int cury= cur.second;visited[curx][cury]=true;//标记该节点访问过for(int i=0;i<4;i++){int nextx=curx+dir[i][0];int nexty=cury+dir[i][1];//判断是否超出边界if(nextx<0||nextx>=grid.size()||nexty<0||nexty>=grid[0].size())continue;if(!visited[nextx][nexty]&&grid[nextx][nexty]=='1'){que.push({nextx,nexty});visited[nextx][nexty]=true;}}}}int numIslands(vector<vector<char>>& grid) {int result=0;int n=grid.size();int m=grid[0].size();vector<vector<bool>>visited(n, vector(m,false));for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(!visited[i][j]&&grid[i][j]=='1'){result++;bfs(grid,visited,i,j );}}}return result;}
};深度优先版本:
class Solution {
public:int dir[4][2]={0,1,1,0,-1,0,0,-1};//定义四个方向void dfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nextx>=grid.size()||nexty<0||nexty>=grid[0].size())continue;if(!visited[nextx][nexty]&&grid[nextx][nexty]=='1'){visited[nextx][nexty]=true;dfs(grid,visited,nextx,nexty);}}}int numIslands(vector<vector<char>>& grid) {int result=0;int n=grid.size();int m=grid[0].size();vector<vector<bool>>visited(n, vector(m,false));for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(!visited[i][j]&&grid[i][j]=='1'){result++;dfs(grid,visited,i,j );}}}return result;}
};参考:代码随想录
相关文章:

图论基础|深度优先dfs、广度优先bfs
dfs 与 bfs 区别 提到深度优先搜索(dfs),就不得不说和广度优先搜索(bfs)有什么区别 先来了解dfs的过程,很多录友可能对dfs(深度优先搜索),bfs(广度优先搜索…...

Python从入门到精通秘籍十七
一、Python的构造方法 在Python中,构造方法是一个特殊的方法,用于创建和初始化类的实例。构造方法的名称是__init__(),它在创建对象时自动调用。 下面是一个示例代码来详细解释Python的构造方法: class Person:def __init__(se…...

Java——抽象类和接口
目录 1.抽象类 1.概念: 2.语法 3.特性 2.接口 1.概念 2.语法 3.特性 1.抽象类 1.概念: 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的…...
)
React—— props校验(非typescript校验类型)
非typescript环境下,当我们在封装组件的时候,接受props时传入的内容,需要做类型检测,那我们可以用props校验进行类型的检查。 props校验允许在创建组件的时候,就约定props的格式、类型等 实现步骤: 导入 …...
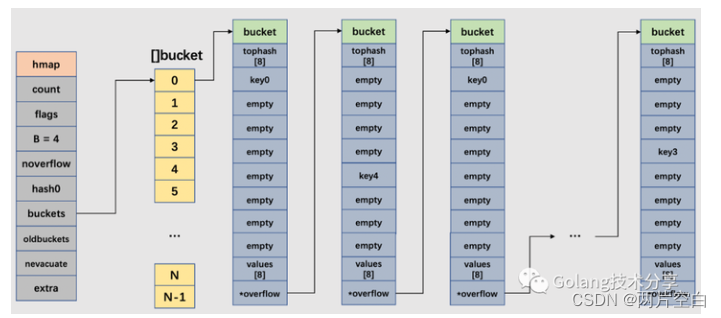
Go——map操作及原理
一.map介绍和使用 map是一种无序的基于key-value的数据结构,Go语言的map是引用类型,必须初始化才可以使用。 1. 定义 Go语言中,map类型语法如下: map[KeyType]ValueType KeyType表示键类型ValueType表示值类型 map类型的变量默认…...
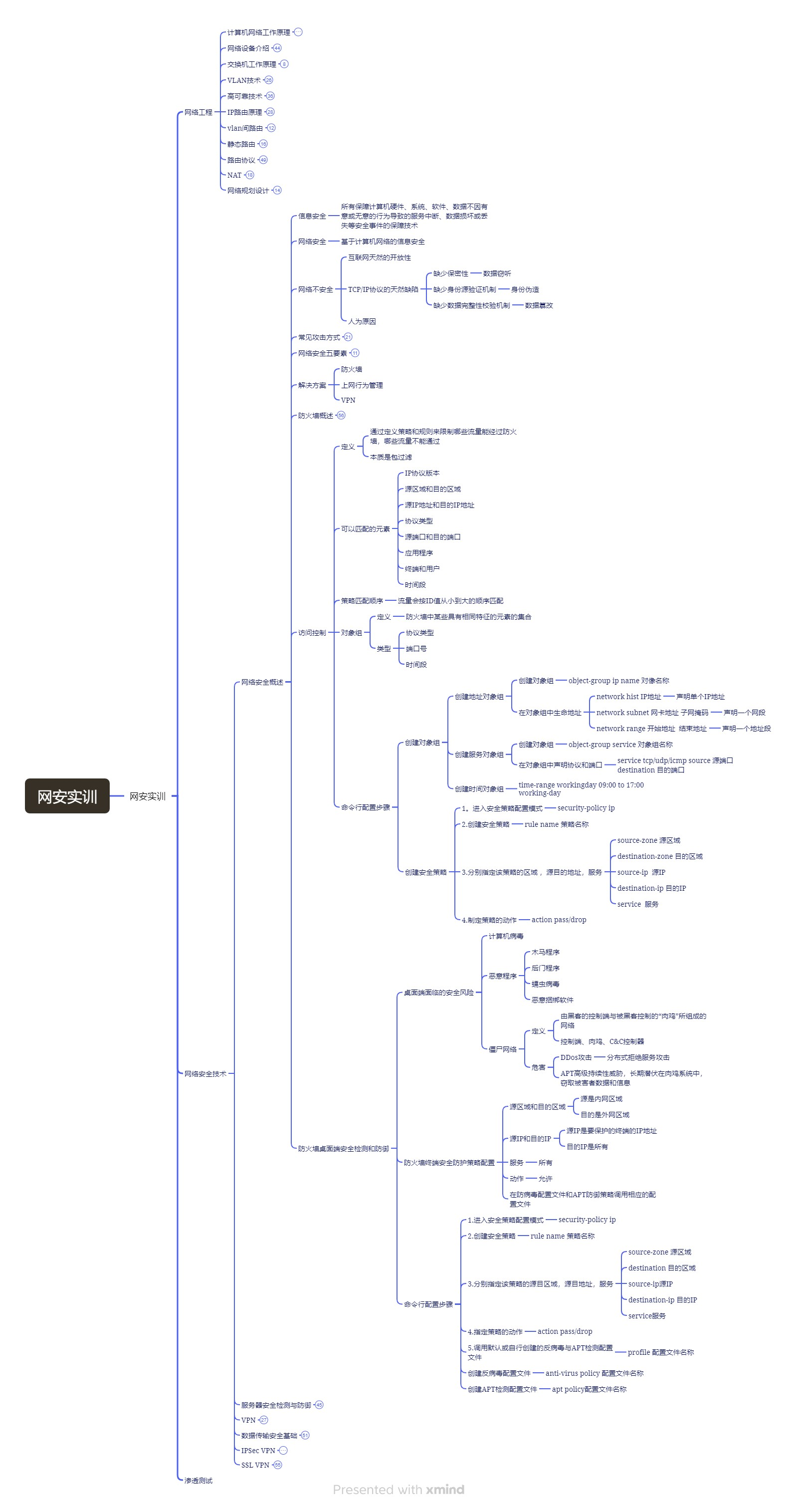
网络安全实训Day9
写在前面 访问控制和防火墙桌面端安全检测与防御 网络安全实训-网络安全技术 网络安全概述 访问控制 定义:通过定义策略和规则来限制哪些流量能经过防火墙,哪些流量不能通过。本质是包过滤 可以匹配的元素 IP协议版本 源区域和目的区域 源IP地址和目…...
之虚拟机centos搭建k8s集群)
kubernetes实战(1)之虚拟机centos搭建k8s集群
一,环境准备 centos7系统,每个系统2c2g,40g,centos7下载地址:centos-7.9.2009-isos-x86_64安装包下载_开源镜像站-阿里云 # 每个节点分别设置对应主机名 hostnamectl set-hostname master hostnamectl set-hostname …...
基于python+vue分类信息服务平台移动端的设计与实现flask-django-php-nodejs
分类信息服务平台是在Android操作系统下的应用平台。为防止出现兼容性及稳定性问题,框架选择的是django,Android与后台服务端之间的数据存储主要通过MySQL。用户在使用应用时产生的数据通过 python等语言传递给数据库。通过此方式促进分类信息服务平台信…...
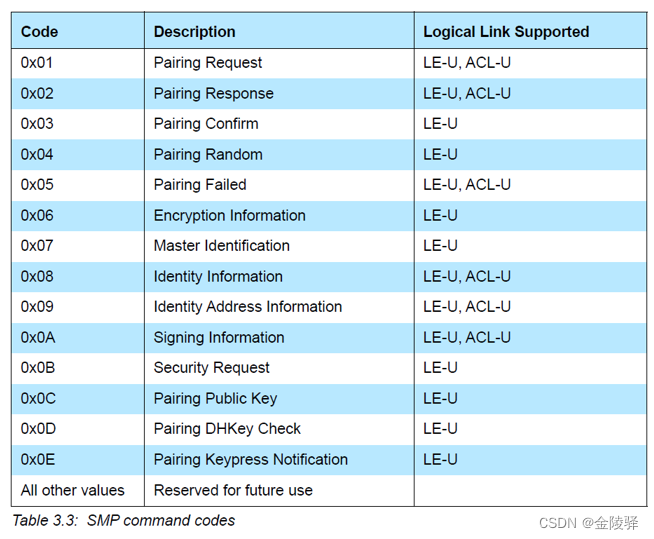
【蓝牙协议栈】【BLE】低功耗蓝牙配对绑定过程分析(超详细)
1. 精讲蓝牙协议栈(Bluetooth Stack):SPP/A2DP/AVRCP/HFP/PBAP/IAP2/HID/MAP/OPP/PAN/GATTC/GATTS/HOGP等协议理论 2. 欢迎大家关注和订阅,【蓝牙协议栈】和【Android Bluetooth Stack】专栏会持续更新中.....敬请期待!…...
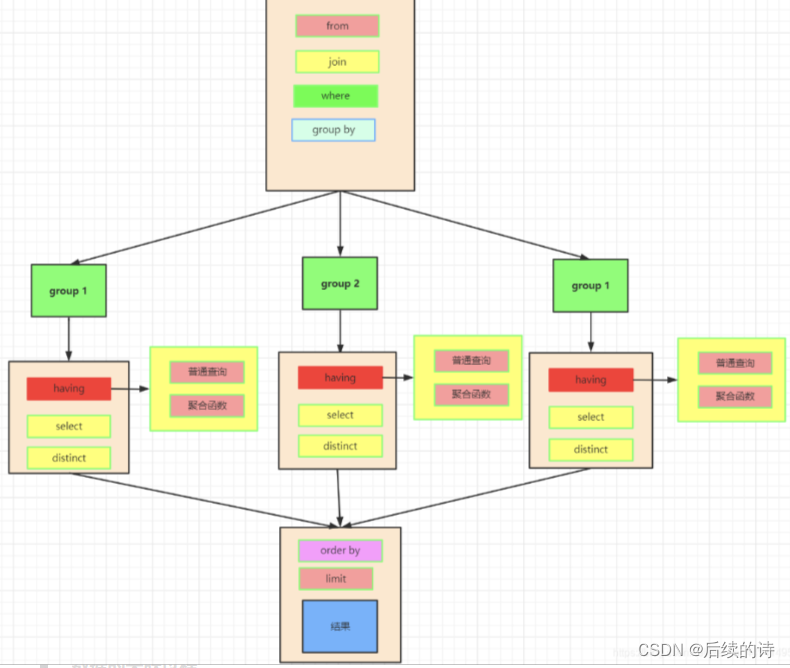
MySQL表内容的增删查改
在前面几章的内容中我们学习了数据库的增删查改,表的增删查改,这一篇我们来学习一下对表中的内容做增删查改。 CRUD : Create(创建), Retrieve(读取),Update(更新),Delete(删除) 1.创建Create 我们先创建…...

Java的三大特性之一——多态(完)
前言 http://t.csdnimg.cn/0CAuc 在上一篇我们已经详讲了继承特性,在这我们将进行最后一个也是最重要的特性讲解——多态 在讲解之前我们需要具备对向上转型以及方法重写的初步了解,这有助于我们对多态的认识 1.向上转型 即实际就是创建一个子类对象…...
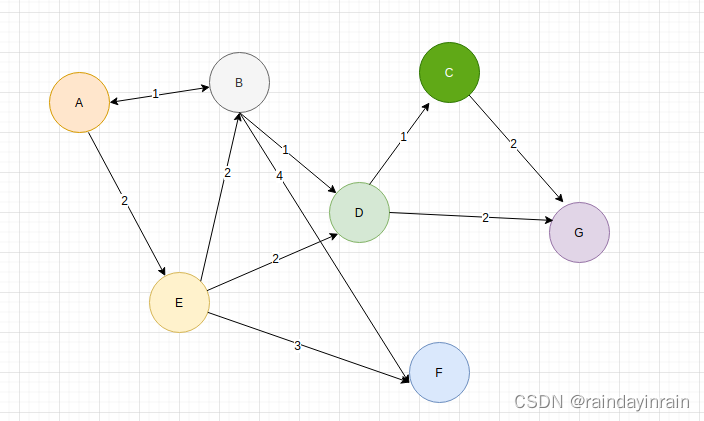
算法-最短路径
图的最短路径问题是一个经典的计算机科学和运筹学问题,旨在找到图中两个顶点之间的最短路径。这种问题在多种场景中都有应用,如网络路由、地图导航等。 解决图的最短路径问题有多种算法,其中最著名的包括: 1.迪杰斯特拉算法 (1).…...
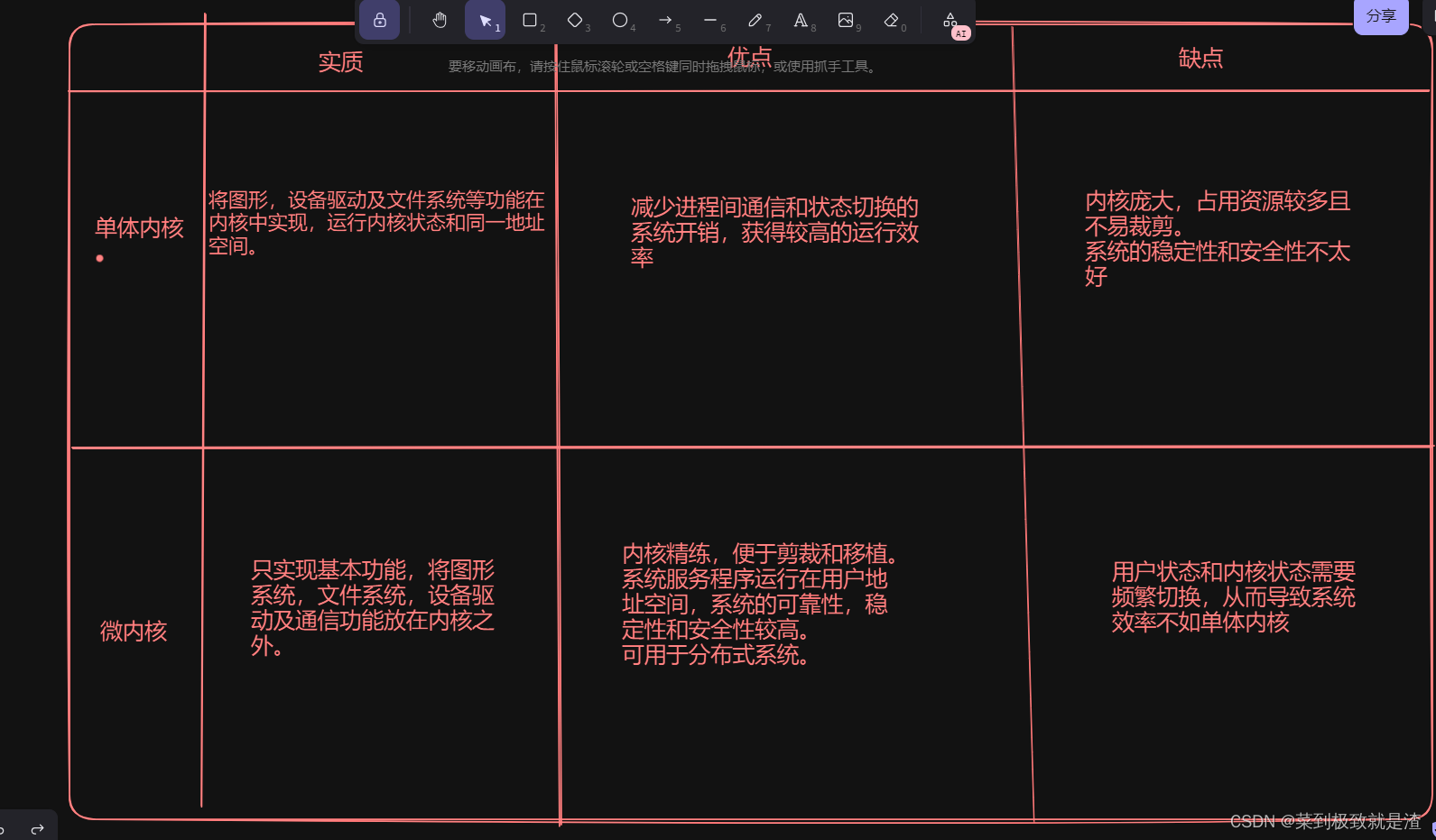
【软考---系统架构设计师】特殊的操作系统介绍
目录 一、嵌入式系统(EOS) (1)嵌入式系统的特点 (2)硬件抽象层 (3)嵌入式系统的开发设计 二、实时操作系统(RTOS) (1)实时性能…...
)
大模型: 提示词工程(prompt engineering)
文章目录 一、什么是提示词工程二、提示词应用1、提示技巧一:表达清晰2、提示词技巧2:设置角色 一、什么是提示词工程 提示词工程主要是用于优化与大模型交互的提示或查询操作,其目的在于能够更加准确的获取提问者想要获取的答案,…...

RabbitMQ的事务机制
想要保证发送者一定能把消息发送给RabbitMQ,一种是通过Confirm机制,另一种就是通过事务机制。 RabbitMQ的事务机制,允许生产者将一组操作打包成一个原子事务单元,要么全部执行成功,要么全部失败。事务提供了一种确保消…...
41 物体检测和目标检测数据集【李沐动手学深度学习v2课程笔记】
目录 1. 物体检测 2. 边缘框实现 3.数据集 4. 小结 1. 物体检测 2. 边缘框实现 %matplotlib inline import torch from d2l import torch as d2ld2l.set_figsize() img d2l.plt.imread(../img/catdog.jpg) d2l.plt.imshow(img);#save def box_corner_to_center(boxes):&q…...
)
软件包管理(rpm+yum)
1.介绍软件包安装方式 rpm包安装: rpm是个软件包管理工具,通过.rpm后缀来操作 -i #安装 -q #查询 -l #列出软件包下的文件 -e #卸载 -h, #软件包安装的时候列出哈希标记 (和 -v 一起使用效果更好) -v, #提供更多的详细信息输出 rpm的痛点&#…...

网关层针对各微服务动态修改Ribbon路由策略
目录 一、介绍 二、常规的微服务设置路由算法方式 三、通过不懈努力,找到解决思路 四、验证 五、总结 一、介绍 最近,遇到这么一个需求: 1、需要在网关层(目前使用zuul)为某一个服务指定自定义算法IP Hash路由策…...
)
如何从零开始拆解uni-app开发的vue项目(二)
昨天书写了一篇如何从零开始uni-app开发的vue项目,今天准备写一篇处理界面元素动态加载的案例: 背景:有不同类别的设备,每个设备有每日检查项目、每周检查项目、每年检查项目,需要维保人员,根据不同设备和检查类别对检查项目进行处理,提交数据。 首先看一下界面: &l…...
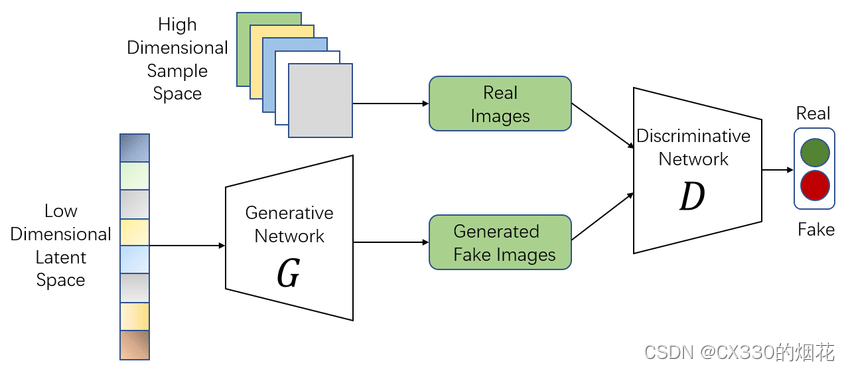
【生成对抗网络GAN】一篇文章讲透~
目录 引言 一、生成对抗网络的基本原理 1 初始化生成器和判别器 2 训练判别器 3 训练生成器 4 交替训练 5 评估和调整 二、生成对抗网络的应用领域 1 图像生成与编辑 2 语音合成与音频处理 3 文本生成与对话系统 4 数据增强与隐私保护 三、代码事例 四、生成对抗…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
