突破编程_C++_查找算法(分块查找)
1 算法题 :使用分块算法在有序数组中查找指定元素
1.1 题目含义
在给定一个有序数组的情况下,使用分块查找算法来查找数组中是否包含指定的元素。分块查找算法是一种结合了顺序查找和二分查找思想的算法,它将有序数组划分为若干个块,每个块内的元素不必有序,但块与块之间必须保持有序。首先通过块之间的有序性来快速定位到目标元素可能存在的块,然后在该块内进行顺序查找。
1.2 示例
示例 1:
输入:
- 有序数组:[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29]
- 块大小:5
- 目标元素:17
输出:
- 7
说明:
- 数组被划分为 3 个块:[1, 3, 5, 7, 9]、[11, 13, 15, 17, 19] 和 [21, 23, 25, 27, 29]。通过比较块的首个元素,可以确定目标元素 17 在第二个块中。然后在该块内进行顺序查找,找到元素 17 的位置为 7(从 0 开始计数)。
示例 2:
输入:
- 有序数组:[1, 4, 6, 9, 13, 16, 19, 22, 25, 28]
- 块大小:4
- 目标元素:10
输出:
- -1
说明:
- 数组被划分为 3 个块:[1, 4, 6, 9]、[13, 16, 19, 22] 和 [25, 28]。通过比较块的首个元素,可以确定目标元素 10 不在任何一个块中,因此整个数组中也不存在该元素。
示例 3:
输入:
- 有序数组:[]
- 块大小:10
- 目标元素:50
输出:
- -1
说明:
- 有序数组为空,50 不存在于有序数组中,返回 -1。
2 解题思路
2.1 简单分块查找
(1)确定块数:
首先,根据给定的块大小,计算数组可以分成的块数。如果数组长度不是块大小的整数倍,则最后一个块的大小可能会小于块大小。
(2)定位目标块:
遍历数组中的块,通过比较每个块的首个元素和目标元素的大小关系,确定目标元素可能所在的块。如果目标元素小于当前块的首个元素,则目标元素不可能在当前块及之后的块中,可以提前结束遍历。
(3)块内顺序查找:
在定位到的目标块内,使用顺序查找算法来查找目标元素。从目标块的起始位置开始,逐个比较元素直到找到目标元素或遍历完整个块。
(4)返回结果:
如果找到了目标元素,则返回其在数组中的位置(索引)。如果遍历完所有块都没有找到目标元素,则返回表示未找到的标志(如-1)。
2.2 优化块内查找
这种思路在第一种的基础上,对块内查找进行了优化。
(1)确定块数和索引映射:
首先,像第一种思路一样确定块数。然后,可以建立一个索引映射关系,将每个元素映射到其所属的块和块内的相对位置。这样可以在定位到目标块后,直接计算出目标元素在块内的相对位置,减少不必要的比较操作。
(2)定位目标块:
这一步与第一种思路相同,通过比较块的首个元素和目标元素的大小关系,确定目标元素可能所在的块。
(3)块内直接定位:
利用索引映射关系,直接计算出目标元素在块内的相对位置。然后,通过该相对位置访问数组元素,检查是否为目标元素。
(4)返回结果:
如果找到了目标元素,则返回其在数组中的位置(索引)。如果遍历完所有块都没有找到目标元素,则返回表示未找到的标志(如-1)。
3 算法实现代码
3.1 简单分块查找
如下为算法实现代码:
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm> class Solution
{
public:// 分块查找算法实现 int blockSearch(const std::vector<int>& arr, int blockSize, int target) {int n = arr.size();int blockNum = (n + blockSize - 1) / blockSize; // 计算块数,向上取整 // 遍历块,定位目标元素可能所在的块 for (int i = 0; i < blockNum; ++i) {int blockStart = i * blockSize;int blockEnd = std::min(blockStart + blockSize, n); // 块内最后一个元素的索引 // 如果目标元素小于当前块的最小值,则目标元素不可能在当前块及之后的块中 if (target < arr[blockStart]) {break;}// 如果目标元素大于当前块的最大值,则继续查找下一个块 if (target > arr[blockEnd - 1]) {continue;}// 在目标块内进行顺序查找 for (int j = blockStart; j < blockEnd; ++j) {if (arr[j] == target) {return j; // 返回目标元素在数组中的位置 }}}return -1; // 未找到目标元素 }
};
这段代码首先计算了块数 blockNum,然后遍历每个块,通过比较块的首个元素 arr[blockStart] 和最后一个元素 arr[blockEnd - 1] 与目标元素 target 的大小关系,来确定目标元素可能所在的块。如果目标元素小于当前块的最小值,则它不可能在当前块及之后的块中,可以提前结束遍历。如果目标元素在当前块内,则在该块内进行顺序查找,直到找到目标元素或遍历完整个块。如果遍历完所有块都没有找到目标元素,则返回 -1 表示未找到。
调用上面的算法,并得到输出:
int main()
{Solution s;std::vector<int> arr = { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29 };int blockSize = 5; // 块大小 int target = 17; // 目标元素 int index = s.blockSearch(arr, blockSize, target);if (index != -1) {std::cout << "Element found at index: " << index << std::endl;}else {std::cout << "Element not found in the array." << std::endl;}return 0;
}
上面代码的输出为:
Element found at index: 8
3.2 优化块内查找
如下为算法实现代码:
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <unordered_map> class Solution
{
public:// 分块查找算法实现 int blockSearch(const std::vector<int>& arr, int blockSize, int target) {int n = arr.size();int blockNum = (n + blockSize - 1) / blockSize; // 计算块数,向上取整 std::unordered_map<int, std::pair<int, int>> blockIndicesAndOffsets; // 存储块索引和块内偏移量 computeBlockIndicesAndOffsets(arr, blockSize, blockIndicesAndOffsets);// 遍历块,定位目标元素可能所在的块 for (int i = 0; i < blockNum; ++i) {int blockStart = i * blockSize;int blockEnd = std::min(blockStart + blockSize, n); // 块内最后一个元素的索引 // 如果目标元素小于当前块的最小值,则目标元素不可能在当前块及之后的块中 if (target < arr[blockStart]) {break;}// 如果目标元素大于当前块的最大值,则继续查找下一个块 if (target > arr[blockEnd - 1]) {continue;}// 检查目标元素是否在块内,并返回其位置 auto it = blockIndicesAndOffsets.find(target);if (it != blockIndicesAndOffsets.end() && it->second.first == i) {return blockStart + it->second.second; // 返回目标元素在数组中的位置 }}return -1; // 未找到目标元素 }private:// 计算并存储每个元素的块索引和块内偏移量 void computeBlockIndicesAndOffsets(const std::vector<int>& arr, int blockSize,std::unordered_map<int, std::pair<int, int>>& blockIndicesAndOffsets) {int n = arr.size();for (int i = 0; i < n; ++i) {int blockIndex = i / blockSize;int offset = i % blockSize;blockIndicesAndOffsets[arr[i]] = { blockIndex, offset };}}
};
在这个代码中,computeBlockIndicesAndOffsets 函数用于计算并存储每个元素的块索引和块内偏移量。optimizedBlockSearch 函数首先通过遍历块来定位目标元素可能所在的块,然后直接检查目标元素是否在预计算的块索引和偏移量映射中,并且其块索引与当前遍历的块索引相匹配。如果找到匹配项,则直接返回目标元素在数组中的位置。
注意:这种方法只适用于数组不会改变的情况,因为一旦数组发生变化,就需要重新计算块索引和偏移量。此外,如果数组非常大或者元素非常多,存储块索引和偏移量映射可能会消耗大量内存。因此,在实际应用中,需要根据具体情况权衡这种优化方法的利弊。
4 测试用例
以下是针对上面算法的测试用例,基本覆盖了各种情况:
(1)基础测试用例
输入:数组 arr = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29},块大小 blockSize = 5,目标元素 target = 17
输出:找到目标元素 17,位置为 8
说明:目标元素位于第三个块内,算法能够正确找到其位置。
(2)边界测试用例
输入:数组 arr = {1, 3, 5, 7, 9},块大小 blockSize = 3,目标元素 target = 1
输出:找到目标元素 1,位置为 0
说明:目标元素位于数组的第一个元素,算法能够正确处理边界情况。
输入:数组 arr = {1, 3, 5, 7, 9},块大小 blockSize = 3,目标元素 target = 9
输出:找到目标元素 9,位置为 4
说明:目标元素位于数组的最后一个元素,算法能够正确处理边界情况。
(3)块内查找测试用例
输入:数组 arr = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29},块大小 blockSize = 5,目标元素 target = 23
输出:找到目标元素 23,位置为 12
说明:目标元素位于第三个块内,但不是块的首个或末尾元素,算法能够在块内正确找到目标元素。
(4)未找到目标元素测试用例
输入:数组 arr = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29},块大小 blockSize = 5,目标元素 target = 30
输出:未找到目标元素 30
说明:目标元素不在数组中,算法能够正确处理未找到目标元素的情况。
(5)空数组测试用例
输入:数组 arr = {},块大小 blockSize = 5,目标元素 target = 1
输出:未找到目标元素 1
说明:数组为空,算法能够正确处理空数组的情况。
(6)单个块测试用例
输入:数组 arr = {1, 2, 3, 4, 5},块大小 blockSize = 5,目标元素 target = 3
输出:找到目标元素 3,位置为 2
说明:整个数组只包含一个块,算法能够正确处理单个块的情况。
相关文章:
)
突破编程_C++_查找算法(分块查找)
1 算法题 :使用分块算法在有序数组中查找指定元素 1.1 题目含义 在给定一个有序数组的情况下,使用分块查找算法来查找数组中是否包含指定的元素。分块查找算法是一种结合了顺序查找和二分查找思想的算法,它将有序数组划分为若干个块&#x…...

学习java第二十二天
IOC 容器具有依赖注入功能的容器,它可以创建对象,IOC 容器负责实例化、定位、配置应用程序中的对象及建立这些对象间的依赖。通常new一个实例,控制权由程序员控制,而"控制反转"是指new实例工作不由程序员来做而是交给Sp…...

每天学习一个Linux命令之systemctl
每天学习一个Linux命令之systemctl 介绍 在Linux系统中,systemctl命令是Systemd初始化系统的核心管理工具之一。systemd是用来启动、管理和监控运行在Linux上的系统的第一个进程(PID 1),它提供了一整套强大的工具和功能…...

【机器学习入门】人工神经网络(二)卷积和池化
系列文章目录 第1章 专家系统 第2章 决策树 第3章 神经元和感知机 识别手写数字——感知机 第4章 线性回归 第5章 逻辑斯蒂回归和分类 第5章 支持向量机 第6章 人工神经网络(一) 文章目录 系列文章目录前言一、卷积神经连接的局部性平移不变性 二、卷积处理图像的效果代码二、…...

公司内部局域网怎么适用飞书?
随着数字化办公的普及,企业对于内部沟通和文件传输的需求日益增长。飞书作为一款集成了即时通讯、云文档、日程管理、视频会议等多种功能的智能协作平台,已经成为许多企业提高工作效率的首选工具。本文将详细介绍如何在公司内部局域网中应用飞书…...
JVM的知识
什么是JVM 1.JVM: JVM其实就是运行在 操作系统之上的一个特殊的软件。 2.JVM的内部结构: (1)因为栈会将执行的程序弹出栈。 (2)垃圾99%的都是在堆和方法区中产生的。 类加载器:加载class文件。…...

大模型日报2024-03-24
利用LLMs评分及解释K-12科学答案 摘要: 本文研究了在K-12级科学教育中使用大型语言模型(LLMs)对短答案评分及解释。研究采用GPT-4结合少量样本学习和活跃学习,通过人机协作提供有意义的评估反馈。 MathVerse:多模态LLM解数学题效果…...

Android kotlin全局悬浮窗全屏功能和锁屏页面全屏悬浮窗功能一
1.前言 在进行app应用开发中,在实现某些功能中要求实现悬浮窗功能,分为应用内悬浮窗 ,全局悬浮窗和 锁屏页面悬浮窗功能 等,接下来就来实现这些悬浮窗全屏功能,首选看下第一部分功能实现 2.kotlin全局悬浮窗全屏功能和锁屏页面全屏悬浮窗功能一分析 悬浮窗是属于Androi…...

图像识别在安防领域的应用
图像识别技术在安防领域有着广泛的应用,它通过分析和理解图像中的视觉信息,为安防系统提供了强大的辅助功能。以下是一些主要的应用领域: 人脸识别:人脸识别技术是安防领域中最常见的应用之一。它可以帮助系统识别和验证个人身份…...

前端面试集中复习 - http篇
1. http请求方式 HTTP请求方式有哪些:GET POST PUT DELETE OPTIONS 1) GET POST 的区别? 场景上: GET 用于获取资源而不对服务器资源做更改提交的请求,多次执行结果一致。用于获取静态数据,幂等。 POST࿱…...
C++ - 类和对象(上)
目录 一、类的定义 二、访问限定符 public(公有) protected(保护) private(私有) 三、类声明和定义分离 四、外部变量和成员变量的区别与注意 五、类的实例化 六、类对象的模型 七、类的this指针…...

mysql基础4sql优化
SQL优化 插入数据优化 如果我们需要一次性往数据库表中插入多条记录,可以从以下三个方面进行优化。 insert into tb_test values(1,tom); insert into tb_test values(2,cat); insert into tb_test values(3,jerry);-- 优化方案一:批量插入数据 Inser…...

实现Spring Web MVC中的文件上传功能,并处理大文件和多文件上传
实现Spring Web MVC中的文件上传功能,并处理大文件和多文件上传 在Spring Web MVC中实现文件上传功能并处理大文件和多文件上传是一项常见的任务。下面是一个示例,演示如何在Spring Boot应用程序中实现这一功能: 添加Spring Web依赖&#x…...
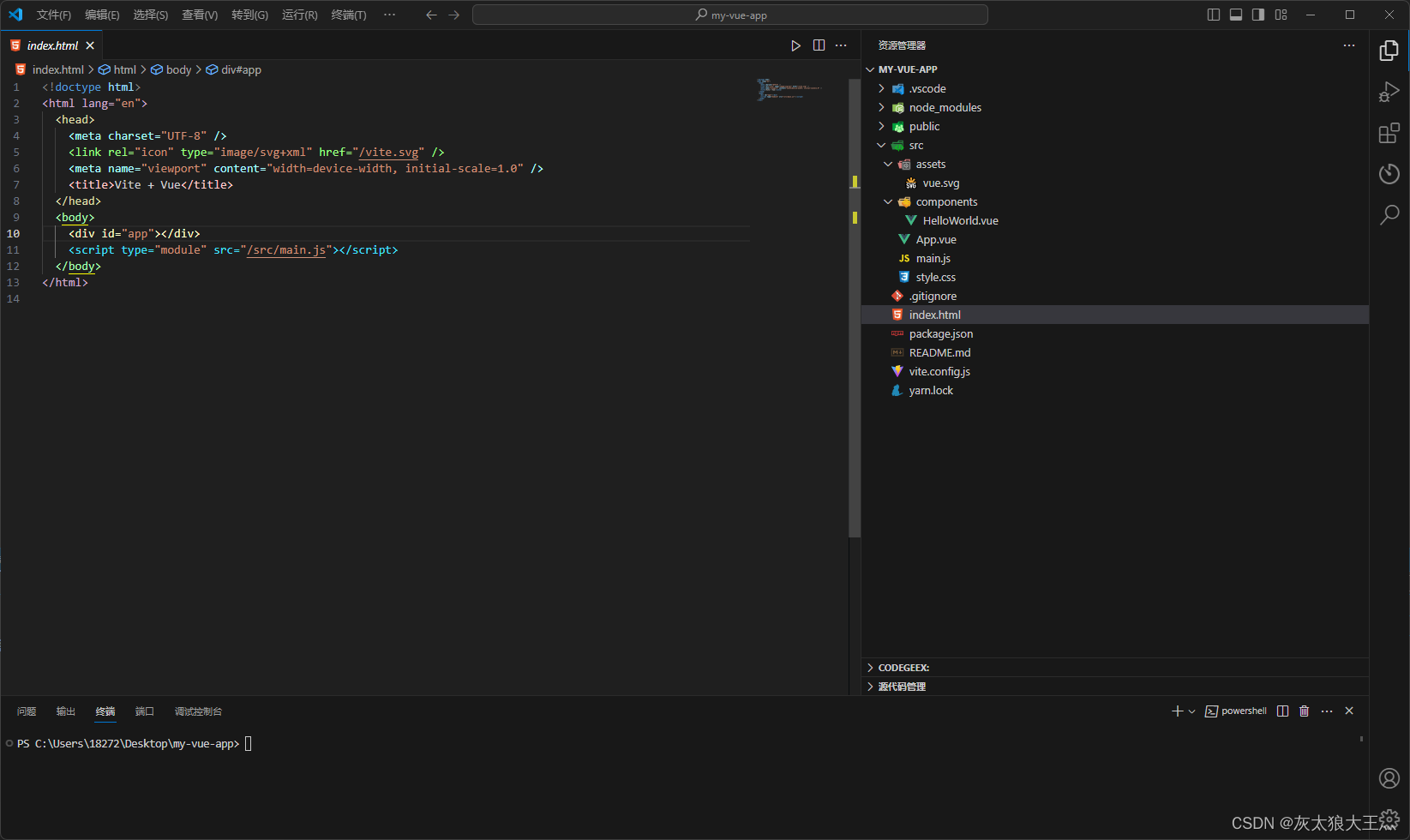
搭建vite项目
文章目录 Vite 是一个基于 Webpack 的开发服务器,用于开发 Vue 3 和 Vite 应用程序 一、创建一个vite项目二、集成Vue Router1.安装 vue-routernext插件2.在 src 目录下创建一个名为 router 的文件夹,并在其中创建一个名为 index.js 的文件。在这个文件中…...

Docker 安装mysql 主从复制
目录 1 MySql主从复制简介 1.1 主从复制的概念 1.2 主从复制的作用 2. 搭建主从复制 2.1 pull mysql 镜像 2.2 新建主服务器容器实例 3307 2.2.1 master创建 my.cnf 2.2.2 重启master 2.2.3 进入mysql 容器,创建同步用户 2.3 新建从服务器容器实例 3308…...

GPT每日面试题—如何实现二分查找
充分利用ChatGPT的优势,帮助我们快速准备前端面试。今日问题:如何实现二分查找? Q:如果在前端面试中,被问到如何实现二分查找,如果回答比较好,给出必要的代码示例 A:当被问到如何实…...

机器学习神经网络由哪些构成?
机器学习神经网络通常由以下几个主要组件构成: 1. **输入层(Input Layer)**:输入层接受来自数据源(例如图像、文本等)的原始输入数据。每个输入特征通常表示为输入层中的一个节点。 2. **隐藏层ÿ…...

代码随想录算法训练营day19 | 二叉树阶段性总结
各个部分题目的代码题解都在我往日的二叉树的博客中。 (day14到day22) 目录 二叉树理论基础二叉树的遍历方式深度优先遍历广度优先遍历 求二叉树的属性二叉树的修改与制造求二叉搜索树的属性二叉树公共最先问题二叉搜索树的修改与构造总结 二叉树理论基础 二叉树的理论基础参…...

数据库引论:3、中级SQL
一些更复杂的查询表达 3.1 连接表达式 拼接多张表的几种方式 3.1.1 自然连接 natural join,自动连接在所有共同属性上相同的元组 join… using( A 1 , A 2 , ⋯ A_1,A_2,\cdots A1,A2,⋯):使用括号里的属性进行自然连接,除了这些属性之外的共同…...

毕业设计:日志记录编写(3/17起更新中)
目录 3/171.配置阿里云python加速镜像:2. 安装python3.9版本3. 爬虫技术选择4. 数据抓取和整理5. 难点和挑战 3/241.数据库建表信息2.后续进度安排3. 数据处理和分析 3/17 当前周期目标:构建基本的python环境:运行爬虫程序 1.配置阿里云pytho…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
