当前位置：首页 > news >正文

蓝桥杯练习07小兔子爬楼梯

news 2025/9/14 18:07:28

小兔子爬楼梯

介绍

小兔子想去月球上旅行，假设小兔子拥有一个阶梯子，当你爬完层就可以到达月球，小兔子每次可以跳1或者2个台阶，小兔子有多少种跳法可以到达月球呢？
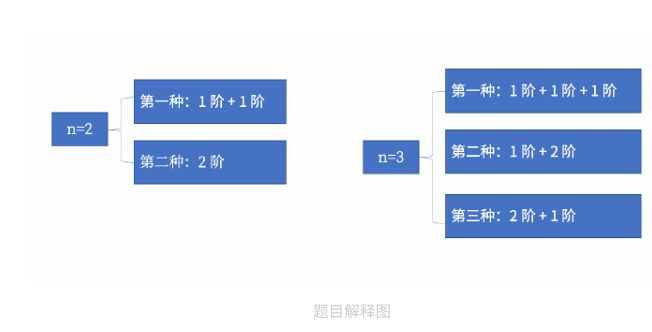
给定n是一个正整数，代表梯子的阶数，当n=2时，小兔子有2种跳法到达月球；当=3时，小兔子有3种跳法跳到月球，以此类推，解释如下图所示：

提示

这里为同学提供一种解题思路。

递归
可以使用递归来实现，具体思路如下：
. 当阶梯数为0时，只有0种方法；当阶梯数为1时，只有1种方法；当阶梯数为2时，只有2种方法，所以当阶梯数小于等于2时，可以直接返回值。
·如果阶梯数大于2，就递归。
解题思路不只这一种，同学们可以自由发挥。

准备

开始答题前，需要先打开本题的项目代码文件夹，目录结构如下：

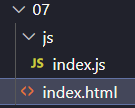
其中：
·js/index.js是实现函数的is代码文件。
·index.html是显示结果的页面。
在浏览器中预览index.html页面效果如下：

目标

请完善js/index.js文件中的代码，让页面呈现如下所示的效果：

代码

html

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>Document</title></head><body><div><p id="result1"></p><p id="result2"></p><p id="result3"></p></div><script src="./js/index.js"></script><script>let r1 = document.getElementById("result1");let r2 = document.getElementById("result2");let r3 = document.getElementById("result3");r1.innerHTML = `2 阶梯子，兔子有 ${climbStairs(2)} 种跳法到达月球。`;r2.innerHTML = `3 阶梯子，兔子有 ${climbStairs(3)} 种跳法到达月球。`;r3.innerHTML = `4 阶梯子，兔子有 ${climbStairs(4)} 种跳法到达月球。`;</script></body>
</html>

js

const climbStairs = (n) => {// TODO：请补充代码/*** 思路：分析可得第n阶梯子的跳法等于第n-1和第n-2阶梯子的跳法之和*/
};
module.exports = climbStairs;

答案

const climbStairs = (n) => {// TODO：请补充代码/*** 思路：分析可得第n阶梯子的跳法等于第n-1和第n-2阶梯子的跳法之和*///法一：递归思想if (n <= 2) {return n} else {return climbStairs(n - 1) + climbStairs(n - 2)}//法二：第1阶梯子有一种跳法 第2阶梯子有2种跳法，用a，b往后移代表第n-1和第n-2阶梯子的跳法// if (n <= 2) {//     return n// }// let a = 1// let b = 2// let c// while (n > 2) {//     c = a + b//后移a，b//     a = b//     b = c//     n--// }// return c//法三：利用解构赋值，整体思想与法二一样// if (n <= 2) {//     return n// }// let a = 1// let b = 2// while (n > 2) {//     // 解构赋值//     [b, a] = [a + b, b]//     n--// }// return b};
module.exports = climbStairs;

容易看出这几个数和斐波拉契数列相关用递归是最简单，后面的两种方法也是一个意思。

知识点

容易看出这几个数和斐波拉契数列相关用递归是最简单，后面的两种方法也是一个意思。

知识点

题还是比较简单也是常见的数列，考的是递归的运用。

蓝桥杯练习07小兔子爬楼梯

小兔子爬楼梯介绍小兔子想去月球上旅行，假设小兔子拥有一个阶梯子，当你爬完层就可以到达月球，小兔子每次可以跳1或者2个台阶，小兔子有多少种跳法可以到达月球呢？ 给定n是一个正整数，代表梯子的阶数&…...

编程日记 2024/3/26 5:45:12

Docker in Docker原理与实战

Docker in Docker (DinD) 是一种在Docker容器内部运行Docker的技术。它允许在一个Docker容器内部创建和管理其他的Docker容器，实现了一个容器内部的容器编排环境。本文将介绍Docker in Docker的原理，并给出一个实际的应用场景。 Docker in Docker的原理…...

编程日记 2024/3/26 5:44:10

Ruoyi若依框架下载流程详细解读（SpringBoot-Vue）

图解： 前端设计： 前端设计一个link文字连接或者按钮（ElementUI）Element - The worlds most popular Vue UI framework 前端请求设计： import request from /utils/request //下载示例模型定义语言的JSON export const…...

编程日记 2024/3/26 5:43:09

【深度学习】Pytorch中实现交叉熵损失计算的方式总结

在PyTorch中，计算交叉熵损失主要有以下几种方式，它们针对不同的场景和需求有不同的实现方式和适用范围： 1. nn.CrossEntropyLoss 类这是最常用且方便的方法，特别适用于多分类任务。nn.CrossEntropyLoss 实际上是同时完成了 sof…...

编程日记 2024/3/26 5:42:08

机器学习：处理jira工单的分类问题

如何根据jira工单的category、reporter自动找到处理它的组呢？这是一个利用机器学习中knn算法的小实践. 目录 Knn算法数据示例分割数据选择Neighbors knn的优缺点机器学习是一种技术，它的目的是给机器学习能力，让它们可以根据数据自己做决定，所以对于训练…...

编程日记 2024/3/26 5:41:07

后端常问面经之操作系统

请简要描述线程与进程的关系,区别及优缺点？ 本质区别：进程是操作系统资源分配的基本单位，而线程是任务调度和执行的基本单位在开销方面：每个进程都有独立的代码和数据空间（程序上下文），程序之…...

编程日记 2024/3/26 5:38:04

RK3568平台 iperf3测试网络性能

一.iperf3简介 iperf是一款开源的网络性能测试工具，主要用于测量TCP和UDP带宽性能。它可以在不同的操作系统上运行，包括Windows、Linux、macOS等。iperf具有简单易用、功能强大、高度可配置等特点，广泛应用于网络性能测试、网络故障诊断和网…...

编程日记 2024/3/26 5:37:03

Spring Boot中实现对特定URL的权限验证：拦截器、切面和安全框架的比较

引言： 在开发Web应用程序时，对特定URL进行权限验证是一项常见的需求。在Spring Boot中，我们有多种选择来实现这一目标，其中包括使用拦截器、切面和专门的安全框架（如Spring Security）。本文将比较这三种方式…...

编程日记 2024/3/26 5:35:01

【能源数据分析-00】能源领域数据集集锦（动态更新）

一、前言大数据科学在能源领域的深度应用，已经深刻改变了这一行业的垂直格局。它为我们提供了宝贵的见解，帮助降低下游市场的成本，使石油生产商能够更好地应对市场繁荣期的需求。近期，石油价格的剧烈下跌给全球经济带来了沉重打…...

编程日记 2024/3/26 5:32:58

数据挖掘与机器学习 1. 绪论

于高山之巅，方见大河奔涌；于群峰之上，便觉长风浩荡 —— 24.3.24 一、数据挖掘和机器学习的定义 1.数据挖掘的狭义定义背景：大数据时代——知识贫乏数据挖掘的狭义定义： 数据挖掘就是从大量的、不完全的、有噪声的、…...

编程日记 2024/3/26 5:27:53

Matlab实现序贯变分模态分解（SVMD）

大家好，我是带我去滑雪！ 序贯变分模态分解(SVMD) 是一种信号处理和数据分析方法。它可以将复杂信号分解为一系列模态函数，每个模态函数代表信号中的特定频率分量。 SVMD 的主要目标是提取信号中的不同频率分量并将其重构为原始信号。SVMD的基…...

编程日记 2024/3/26 5:26:52

云安全与云计算的关系

云计算又被称为网格计算，是分布式计算的一种，能够将大量的数据计算处理程序通过网络“云”分解成多个小程序，然后将这些小程序的结果反馈给用户。云计算主要就是能够解决任务分发，并进行计算结果的合并。云安全则是我国企业创造的…...

编程日记 2024/3/26 5:25:49

1、继承属性变化接口 public partial class MainWindow : Window, INotifyPropertyChanged {// 通知界面属性发生变化public event PropertyChangedEventHandler PropertyChanged;private void RaisePropertyChanged(string propertyName){PropertyChangedEventHandler handle…...

编程日记 2024/3/26 5:24:48

eclipse导入svn项目

1、配置maven 2、用svn引入项目 3一直点击next,到最后选完成。...

编程日记 2024/3/26 5:23:47

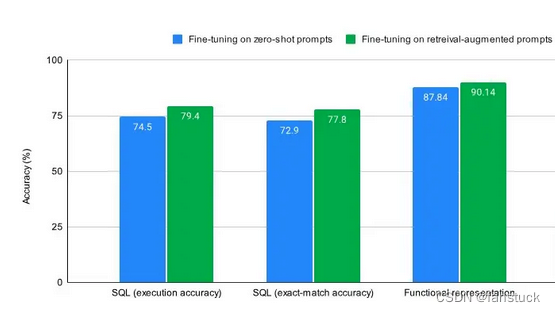
Prompt提示工程上手指南:基础原理及实践(四)-检索增强生成(RAG)策略下的Prompt

前言此篇文章已经是本系列的第四篇文章，意味着我们已经进入了Prompt工程的深水区，掌握的知识和技术都在不断提高，对于Prompt的技巧策略也不能只局限于局部运用而要适应LLM大模型的整体框架去进行改进休整。较为主流的LLM模型框架设计可以基…...

编程日记 2024/3/26 5:22:46

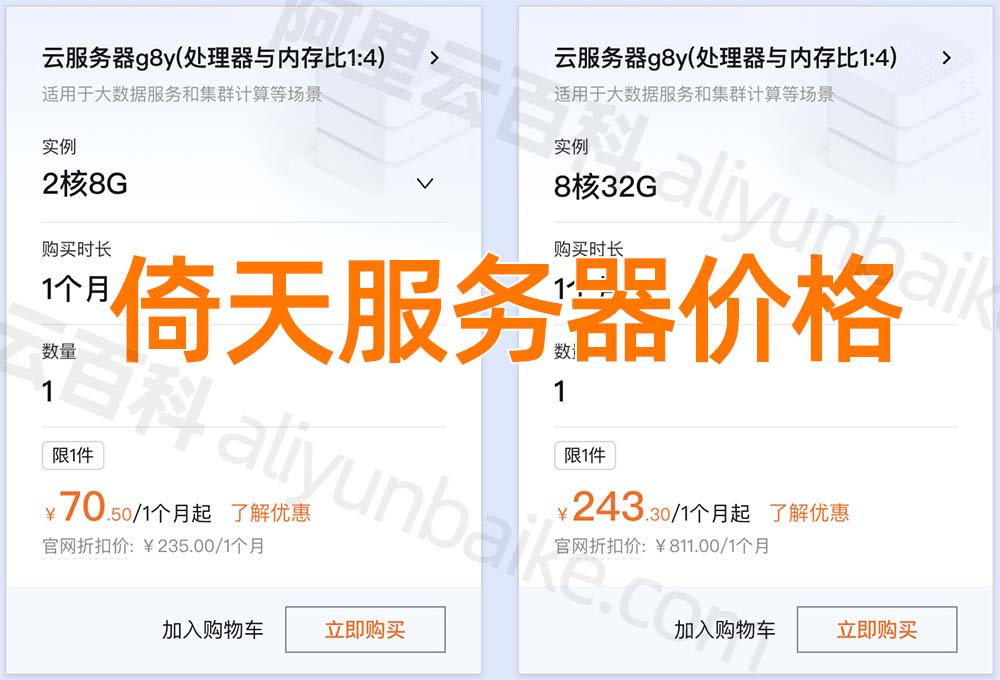
阿里云倚天云服务器怎么样？如何收费？

阿里云倚天云服务器CPU采用倚天710处理器，租用倚天服务器c8y、g8y和r8y可以享受优惠价格，阿里云服务器网aliyunfuwuqi.com整理倚天云服务器详细介绍、倚天710处理器性能测评、CIPU架构优势、倚天服务器使用场景及生态支持： 阿里云倚天云服务…...

编程日记 2024/3/26 5:21:44

海外社交营销为什么用云手机？不用普通手机？

海外社交营销作为企业拓展海外市场的重要手段，正日益受到企业的青睐。云手机以其成本效益和全球性特征，成为海外社交营销领域的得力助手。那么，究竟是什么特性使得越来越多的企业选择利用云手机进行海外社交营销呢？下文将对此进行…...

编程日记 2024/3/26 5:14:39

【Mysql数据库基础05】子查询 where、from、exists子查询、分页查询

where、from、exists子查询、分页查询 1 where子查询1.1 where后面的标量子查询1.1.1 having后的标量子查询 1.2 where后面的列子查询1.3 where后面的行子查询（了解即可） 2 from子查询3 exists子查询（相关子查询）4 分页查询5 联合…...

编程日记 2024/3/26 5:12:37

在Linux/Debian/Ubuntu上通过 Azure Data Studio 管理 SQL Server 2019

Microsoft 提供 Azure Data Studio，这是一种可在 Linux、macOS 和 Windows 上运行的跨平台数据库工具。它提供与 SSMS 类似的功能，包括查询、脚本编写和可视化数据。要在 Ubuntu 上安装 Azure Data Studio，可以按照以下步骤操作&#xff1…...

编程日记 2024/3/26 5:11:36

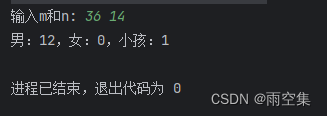
Java代码基础算法练习-搬砖问题-2024.03.25

任务描述： m块砖，n人搬，男搬4，女搬3，两个小孩抬一砖，要求一次全搬完，问男、女、小孩各若干？ 任务要求： 代码示例： package M0317_0331;import java.util.S…...

编程日记 2024/3/26 5:10:35

业务系统对接大模型的基础方案：架构设计与关键步骤

业务系统对接大模型：架构设计与关键步骤在当今数字化转型的浪潮中，大语言模型（LLM）已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中，不仅可以优化用户体验，还能为业务决策提供…...

编程新知 2025/9/14 10:14:39

Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务

通过akshare库，获取股票数据，并生成TabPFN这个模型可以识别、处理的格式，写一个完整的预处理示例，并构建一个预测未来 3 天股价涨跌的分类任务用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务，进行预测并输…...

编程新知 2025/9/12 10:25:58

中医有效性探讨

文章目录西医是如何发展到以生物化学为药理基础的现代医学？传统医学奠基期（远古 - 17 世纪）近代医学转型期（17 世纪 - 19 世纪末）现代医学成熟期（20世纪至今） 中医的源远流长和一脉相承远古至…...

编程新知 2025/9/6 8:07:57

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法：使用 MyBatis 的 <foreach> 标签和批处理模式（ExecutorType.BATCH）。方法一：使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

深入理解Optional：处理空指针异常

1. 使用Optional处理可能为空的集合在Java开发中，集合判空是一个常见但容易出错的场景。传统方式虽然可行，但存在一些潜在问题： // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

编程新知 2025/9/3 13:51:02