双指针的详细教程
双指针算法是一种常用的算法技巧,它通常用于在数组或字符串中进行快速查找、匹配、排序或移动操作。
双指针并非真的用指针实现,一般用两个变量来表示下标(在后面都用指针来表示)
双指针算法使用两个指针在数据结构上进行迭代,并根据问题的要求移动这些指针。
双指针往往也和单调性、排序联系在一起,在数组的区间问题上,暴力法的时间复杂度往往都是O(n^2)的,但双指针利用“单调性”可以优化到O(n)
常见的双指针模型有
(1)对撞指针
指的是两个指针left、right分别指向序列的第一个元素和最后一个元素
然后I指针不断递增,r不断递减,直到两个指针的值相撞后错开(即l>=r),或者满足其他的特殊条件为止
对撞指针一般是用来解决有序数组或者字符串问题(区间问题)
查找有序数组中满足某些约束条件的一组元素问题:比如二分查找、数字之和等问题。
字符串反转问题:反转字符串,回文数等问题。
1 使用两个指针left,right.left指向序列第一个元素,即:left=1,right指向序列最后一个元素,即:right:n。
2 在循环体中将左右指针相向移动,当满足一定条件时,将左指针右移,left++.当满足另外一定条件时,右指针左移right--
直到两指针相撞(即left==right),或者满足其他要求的特殊条件时,跳出循环体
例题实战
题目描述
给定一个长度为n的字符串S,请你判断字符串S是否时回文
输入描述
输入仅一行包含一个字符串S
1<=|S|<=10^6,保证S只包含大小写字母
输出描述
若字符串S为会问串,则输出Y,否则输出N
输入输出样例
示例 1
abcba
输出Y
回文判定
对撞指针,每次判断s[l]和s[r]是否相等。如果相等,进一步移动,否则直接判断“不是回文串”
(2)快慢指针
快慢指针一般比对撞指针更难想,更难写。
指的是两个指针,从同一侧开始遍历序列,且移动的步长一个块,一个慢
移动快的指针被称为快指针,一动漫的指针被称为慢指针
为了方便理解,我们称快指针为r,慢指针为l,这样慢指针和快指针构成的区间为[l,r]
两个指针以不同的速度,不同策略移动,直到快指针移动到数组尾端,或者两指针相交,或者满足其他特殊条件为止。
1.使用两个指针l,r.一般l指向序列的第一个元素,即:l=1,r一般指向序列第零个元素,即:r=0。即初始时区间[l,r]=[1,0]表示为空区间。
2.在循环体中将左右指针向右移动。当满足一定条件时,将慢指针右移,即l++。当满足另外一定条件时(也可能不需要满足条件),将快指针右移,即r++,保持[l,r]为合法区间
3.到指针移动到数组尾端(即l==n且r==n),或者两指针相交,或者满足其他特殊条件时,跳出循环
例题
给定一个长度为n的序列a1,a2,...an和一个常数S
对于一个连续区间如果它的区间和大于或等于S,则称它为美丽区间
对于一个美丽区间,如果区间长度越短,它越美丽
请你从序列中找出最美丽的区间
输入描述
第一含包含两个整数n,S,其含义如题所述
接下来一行包含n个整数,分别表示a1,a2,...an
输出描述
输出共遗憾,包含一个整数,表示最美丽的区间长度
若不存在任何美丽区间,则输出0
相关文章:

双指针的详细教程
双指针算法是一种常用的算法技巧,它通常用于在数组或字符串中进行快速查找、匹配、排序或移动操作。 双指针并非真的用指针实现,一般用两个变量来表示下标(在后面都用指针来表示) 双指针算法使用两个指针在数据结构上进行迭代&a…...
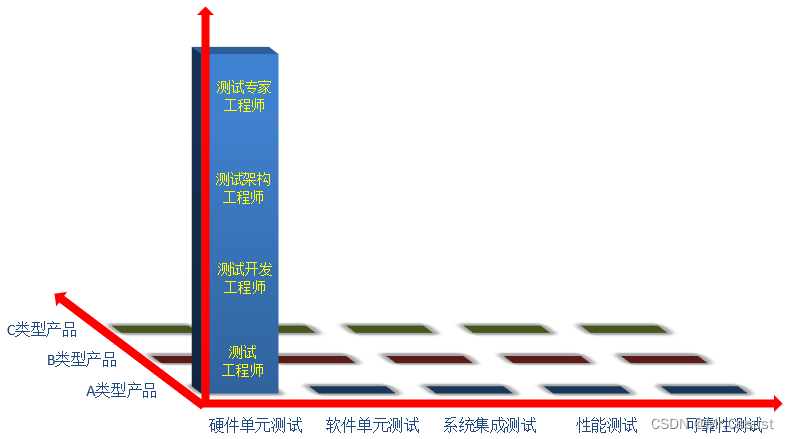
【Review+预测】测试架构演进的曲折之路
文章目录 前言 一、“原始”阶段 二、“小打小闹”阶段 三、“小米加步枪”阶段 四、“摩托化部队”阶段 五、“骑兵连”阶段 六、“海军陆战队”阶段 七、“社区型组织”阶段 前言 近期公司的测试团队需要重新组织安排,本着谦虚谨慎的态度,我从…...

2015年认证杯SPSSPRO杯数学建模D题(第二阶段)城市公共自行车全过程文档及程序
2015年认证杯SPSSPRO杯数学建模 D题 城市公共自行车 原题再现: 城市交通问题直接影响市民的生活和工作。在地形平坦的城市,公共自行车出行系统是一种很好的辅助手段。一般来说,公共自行车出行系统由数据中心、驻车站点、驻车桩、自行车&…...
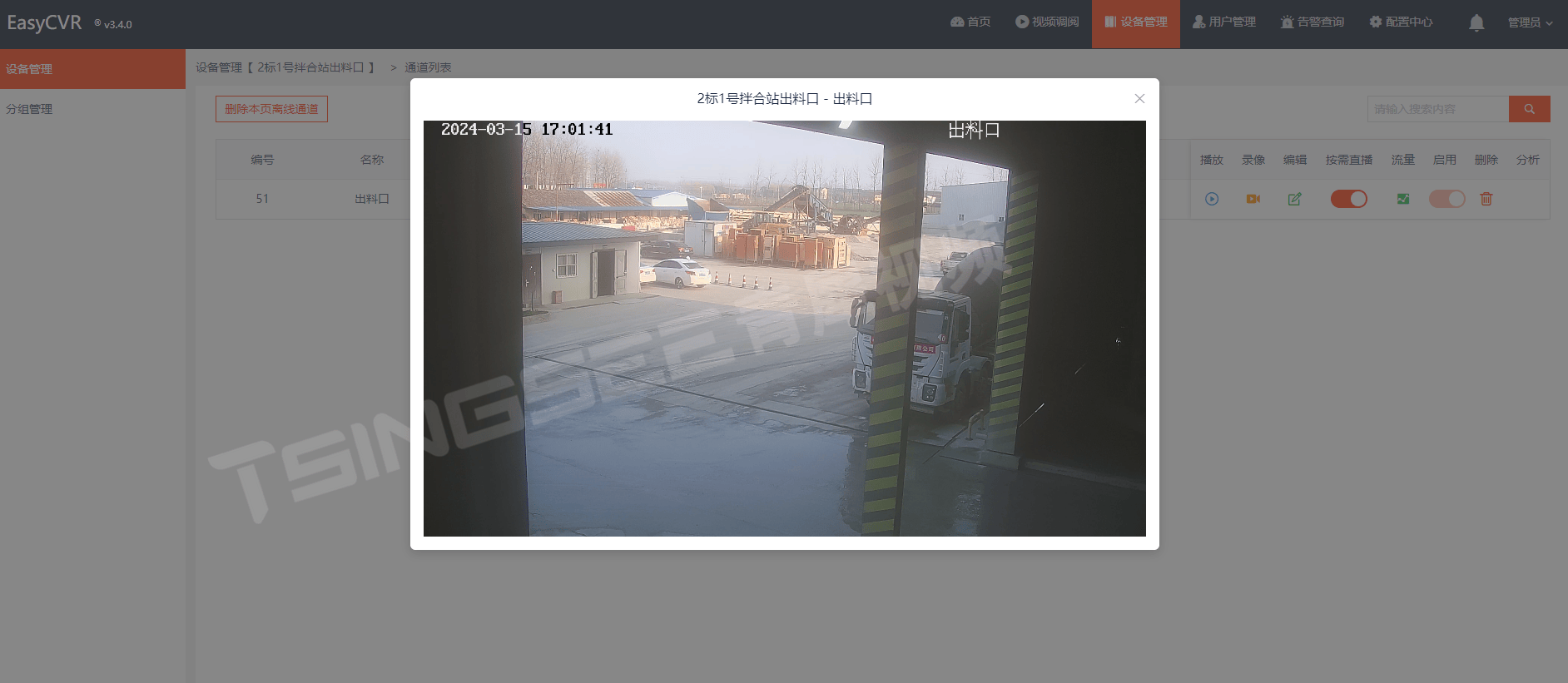
视频汇聚平台EasyCVR启用图形验证码之后调用login接口的操作方法
视频综合管理平台EasyCVR视频监控系统支持多协议接入、兼容多类型设备,平台可以将区域内所有部署的监控设备进行统一接入与集中汇聚管理,实现对监控区域的实时高清视频监控、录像与存储、设备管理、云台控制、语音对讲、级联共享等,在监控中心…...
【数据结构】非线性结构——二叉树
文章目录 前言1.树型结构1.1树的概念1.2树的特性1.3树的一些性质1.4树的一些表示形式1.5树的应用2.二叉树 2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.4 二叉树的存储2.5 二叉树的基本操作 前言 前面我们都是学的线性结构的数据结构,接下来我们就需要来学习非…...
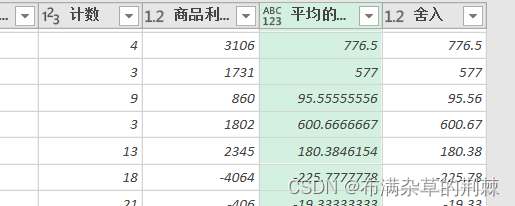
数据分析POWER BI之power query
1.导入数据 ctrla全选--数据--获取数据--其他来源--来自表格/区域 导入数据,进入编辑模式 2.整理与清除 清除:删除所选列的非打印字符 转换--格式--清除 修整:删除前面和后面的空格 转换---格式---修整(修整后前面后面的空格没有了…...

【c语言】详解操作符(上)
1. 操作符的分类 2. 原码、反码、补码 整数的2进制表示方法有三种,即原码、反码、补码 有符号整数的三种表示方法均有符号位和数值位两部分,2进制序列中,最高位的1位是被当做符号位其余都是数值位。 符号位都是用0表示“正”,用…...

VR全景展示:传统制造业如何保持竞争优势?
在结束不久的两会上,数字化经济和创新技术再度成为了热门话题。我国制造产业链完备,但是目前依旧面临着市场需求不足、成本传导压力加大等因素影响,那么传统制造业该如何保持竞争优势呢? 在制造行业中,VR全景展示的应用…...
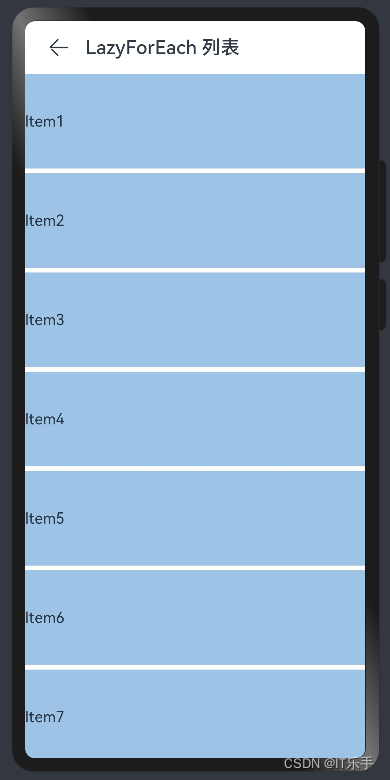
2.7、创建列表(List)
概述 列表是一种复杂的容器,当列表项达到一定数量,内容超过屏幕大小时,可以自动提供滚动功能。它适合用于呈现同类数据类型或数据类型集,例如图片和文本。在列表中显示数据集合是许多应用程序中的常见要求(如通讯录、…...

solr functionquery函数查询自定义函数实现
Solr是一个开源的搜索平台,基于Apache Lucene库构建,主要用于提供全文搜索的功能。它被设计为一个高度可靠、可扩展的搜索应用服务器。以下是Solr的一些主要使用场景: 全文搜索:Solr最核心的功能是提供全文搜索,它可以…...
如何将 Parallels虚拟机 安装或者迁移到 移动硬盘 or U盘?
本文讨论主题 如何安装 Parallels 虚拟机到移动硬盘和U盘? 已经安装到了mac上的虚拟机如何迁移到移动硬盘活着U盘上? 关于Parallels Deskshop 19 虚拟机 安装激活,文末关注公众号AIshape,回复:PD 进行获取通过将虚拟机安装在外置的移动硬盘U盘上,可以节省mac本身SSD的容…...

大型网站集群管理负载均衡
课程介绍 结合企业大规模应用,解决应用高并发问题,解决单节点故障问题,缓存数据库的应用。学完掌握知识点:企业应用实现四七层负载均衡,以及Nginx等应用的高可用性,Redis缓存数据库的部署应用以及高可用方…...

JAVA使用POI实现Excel单元格合并-02
JAVA使用POI实现Excel单元格合并 实现效果 解释:只要是遇见与前一行相同的数据就合并 引入jar <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>5.2.2</version></depe…...

深入了解 Linux 中的 MTD 设备:/dev/mtd* 与 /dev/mtdblock*
目录 前言一、什么是MTD子系统?二、 /dev/mtd* 设备文件用途注意事项 三、/dev/mtdblock* 设备文件用途注意事项 三、这两种设备文件的关系四、关norflash的一些小知识 前言 在嵌入式Linux系统的世界里,非易失性存储技术扮演着至关重要的角色。MTD&#…...

2、Spring CLI安装
安装 Spring CLI 提供了多种格式,让您选择自己喜欢的安装方法。可下载的制品可从发布页面获取。 二进制发行版 WindowsLinuxMac手动安装(Windows,其他自己看) spring-cli-standalone-<version>-windows.x86_64.zip - 打包了 x86 JDKspring-cli-installer-<versi…...
数据库备份工具(实现数据定时覆盖)
数据库备份工具(实现数据定时覆盖) 永远热爱,永远执着! 工具介绍 自动化测试数据库更新调度程序 这段 Python 脚本自动化了每天定时从生产数据库更新测试数据库的过程。它利用了 schedule 库来安排并执行每天指定时间的更新任务…...

测试环境搭建整套大数据系统(十二:挂载磁盘到hadoop环境)
一:链接硬盘 将硬盘连接到计算机的 SATA 接口或 USB 接口,并确保硬盘通电并处于可用状态。 二:查看硬盘信息 sudo fdisk -l三:创建分区 gdisk /dev/vbd重新扫描磁盘 partprobe /dev/vdb格式化磁盘 mkfs.ext4 /dev/vdb2查看磁…...

Spring事务核心:声明式事务注解式事务
全解:声明式事务和注解事务 在Spring中,事务管理是一个非常重要的特性,它可以帮助开发者在应用程序中实现事务控制。Spring提供了两种事务管理方式:声明式事务和注解事务。 1. 声明式事务 声明式事务是指通过配置文件或注解的方…...

AcWing 1015. 摘花生
Problem: AcWing 1015. 摘花生 文章目录 思路解题方法复杂度Code 思路 这是一个典型的动态规划问题。我们需要在一个二维网格中,从左上角走到右下角,每次只能向右或向下移动,目标是使得经过的路径上的数字之和最大。 我们可以定义dp[i][j]为从…...

Dalle-3、Sora、Stable Diffusion 3 掀起AIGC新浪潮
随着科技的飞速发展,我们迎来了视觉AIGC高光时刻,一个充满无限可能与机遇的新时代。在这个时代里,三大里程碑Dalle-3、Sora和Stable Diffusion 3以其炸裂式的技术发展,引领着AIGC领域的新浪潮。文章首先做相应简要介绍,…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
